多级离心泵流场优化及验证

张权，周盼，率志君，李玩幽

（哈尔滨工程大学动力与能源工程学院，哈尔滨 150001）

离心泵在船舶与海洋工程中应用广泛，提高其设计效率、降低其运行振动和噪声，对绿色船舶设计具有很大的现实意义。

流体激励力是离心泵主要振源之一，通过泵壳及轴承向外传递[1]，研究其对机脚振动影响对减振降噪来说尤为重要。国内外对流体产生的振动已经进行了一定研究，主要有实验[2]和数值模拟[3―5]两种方法，倪永燕对离心泵流体诱导振动进行了详细的总结[6]；Gonzalez[7―9]利用CFD技术对离心泵整机流场进行了非稳态数值模拟，讨论了蜗壳蜗舌附近由于动静干扰引起的压力脉动，且与实验值进行了对比，吻合较好，得到了一些有益的结论。

本文通过切割叶轮、改变隔舌形式对某型多级离心泵进行流场优化，运用RNGk-ε湍流模型计算优化前后的压力脉动和流体激励力以考察流场优化效果，最后测试离心泵的机脚响应变化来间接验证优化效果。

1 计算区域及方法

1.1 计算区域及网络

额定工况下，泵的运行参数为：流量24 m3/h，出口压力0.46 MPa，转速1 460 r/min，三级叶轮叶片数依次为10、7、7。

泵内流道非常复杂，因此采用适应性非常强的四面体非结构化网格。叶轮的几何形状及其中的流体流动非常复杂，而且是运动部件，因此叶轮叶片表面需要做较细致的网格划分。网格数对数值计算结果的准确性和所要求的计算资源影响非常大，因此选择出口压力进行网格灵敏度分析。

图1 网格数对出口压力预测的影响

图1为网格数变化对出口压力预测的影响。从中可以发现，当网格数为2 011 334（图中虚线所示）、节点数数为546 160时，出口压力预测结果准确，并且计算用时比较合理，因此选择这个网格数进行数值计算。计算网格模型如图2。

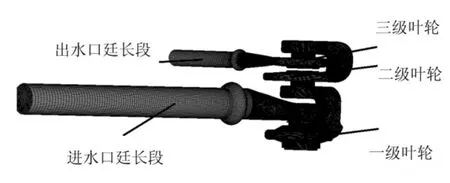
图2 计算网格模型

1.2 计算方法

首先对泵整机流场进行稳态数值计算，在相同条件下，将稳态数值计算的结果作为非稳态计算的初始值。在每一级叶轮和蜗壳间分别形成滑移网格的条件，计算叶轮和蜗壳的相互干涉，得到整机内的非稳态流动特征。

非稳态计算采用全隐式时间格式，选择RNGk-ε湍流模型，固壁上取无滑移边界条件，壁面处采用标准壁面函数处理。采用SIMPLEC算法求解压力速度耦合方程组，控制方程对流项的离散采用二阶迎风格式，扩散项、源项的离散采用二阶中心差分格式。

泵的进口处采用速度进口边界条件，假定进口处速度均匀并垂直于进口断面，给定速度初值；泵出口处满足充分发展的假定，采用压力出口边界条件，认为出口静压值不变。

2 计算结果及分析

通过上述计算方法对计算模型进行了流场计算，在此基础上对原模型进行流场优化，具体优化情况优化如下所示。

2.1 叶轮优化

泵的几何形状规定了叶轮外径D2和壳体隔舌之间的间隙G(见图3)。

图3 叶轮外径和蜗壳示意图

改变G/D2将影响出口脉动[10]。在流量和扬程满足使用的前提下，比值越大越好。改变隔舌间隙（增大G）可以通过切割叶轮的方法来完成，具体切割量由以下比转速计算公式决定

其中n——转速，Q——流量，H——扬程，Ns——比转速。n=1 460 r/min，Q=24 m3/h，H=48.46 m，则Ns=183.5。

考虑到泵组的效率，切割量不能太大，在该比转速下，限定的最大切割量为原叶轮直径的12%左右[10]。这里切割量如下表1所示。

表1 叶轮切割量

单级叶轮流量与叶轮直径成正比[11]，而对于多级叶轮流量与直径的关系没有相应的文献可供参考。本文通过仿真计算切割叶轮后离心泵的流量，给定进口速度边界条件，计算出口流量为23.5 m3/h。而对于该泵当流量处于23.38 m3/h～24.72 m3/h时，均满足使用要求。因此，切割叶轮后流量仍能达到使用要求，不影响泵的性能。为了确定扬程变化情况，切割叶轮前后保证进口压力不变计算出口压力，切割前出口压力为0.46 MPa，切割叶轮后出口压力为0.459 99 MPa，可见切割前后出口压力（扬程）变化并不大，满足使用条件。

2.1.1 叶轮切割前后监测点压力脉动对比

由于流场的压力脉动主要发生在叶轮和蜗壳的流道内，所以关注这两个区域的压力脉动改善情况，观测叶轮优化前后这两个区域内监测点的压力脉动，验证优化效果。叶轮和蜗壳流道内监测点分布图如图4与图5所示。

选取一级叶轮压力脉动较大的点a1、a4、d1和d2进行对比，叶轮优化前后压力脉动对比如图6所示。

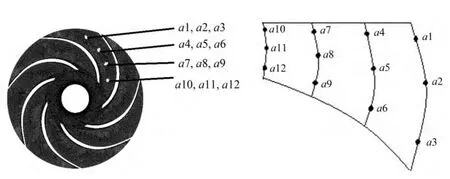
图4 叶轮流道中间截面压力脉动监测点

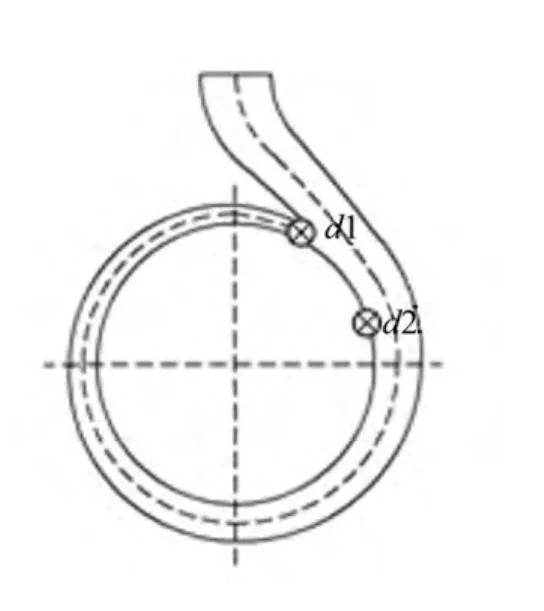
图5 蜗壳区域压力脉动监测点

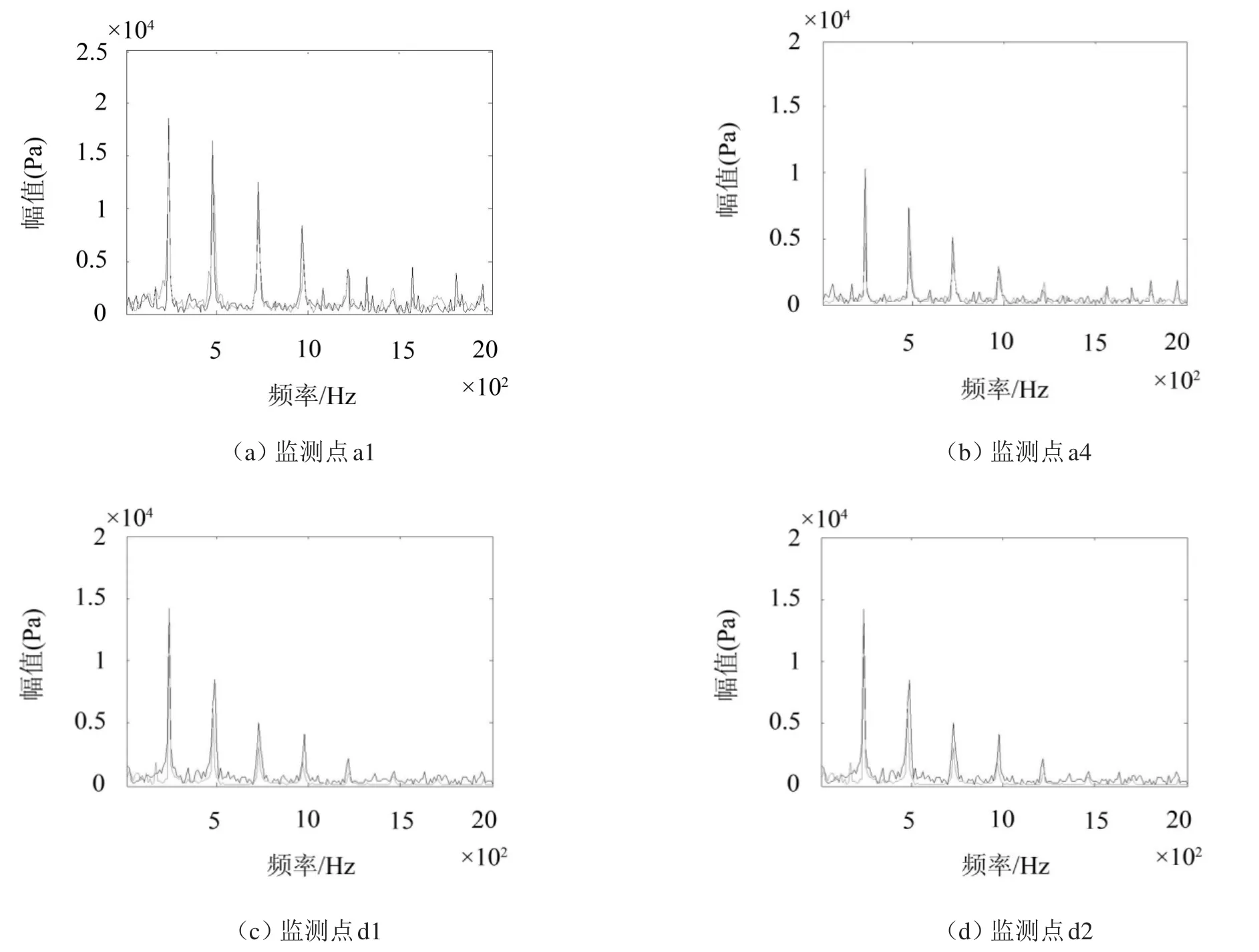
图6 各监测点结果对比

图6中实线谱为切割叶轮前监测点压力脉动，虚线谱为切割叶轮后监测点压力脉动。由于转速为1 460 r/min，三级叶轮叶片数依次为10、7、7，由此可以判断一级叶轮叶频为171 Hz，二三级叶轮叶频为242 Hz。从图中可以看出切割叶轮后叶轮及蜗壳内的压力脉动在叶轮的叶频下幅值有所减小，只有各别叶频较高倍频的峰值略有增大。可见切割叶轮后对叶轮内整体流场的压力脉动有一定的改善效果。

2.1.2 叶轮切割前后流场激励力对比

为了更直观的体现优化效果，将优化前后的叶轮所受流场激励力进行对比，对比结果如图7所示。

图中实谱线为原模型流场激励力，虚谱线为切割叶轮后流场激励力。以一级叶轮受力对比为例，从图7可以看出，切割叶轮后一级叶轮叶频下流体激励力有明显的减小，可见切割叶轮不但使得压力脉动情况有所改善，叶轮受力也有一定减小。但是流场优化对机脚振动的影响需要进一步进行实验验证，二三级叶轮情况与一级叶轮基本相同在此不做具体分析。

图7 一级叶轮z向力

2.2 隔舌优化

常规的单隔舌蜗壳离心泵之所以要有一个最佳的隔舌与叶轮间距，因为间距太小，流体流过隔舌与叶轮外径的间隙时，就会产生较强的压力脉动。若间距过大，尽管流体对隔舌的冲击情况会有所改善，但却会一部分流体在蜗壳内随着叶轮不停地循环，既消耗功率，又减少了流量，同时还会与叶轮出口的流体发生周期性地撞击，从而产生低频振荡，压力脉动增大。

采取阶梯隔舌，便可使两个隔舌各司其职，下隔舌可用来保证泵性能必要的间距，上隔舌则可拉开更大的间距，以使流体对隔舌的冲击情况得到改善[12]。阶梯形隔舌与常规隔舌的区别如图8所示。

2.2.1 优化隔舌前后监测点压力脉动对比

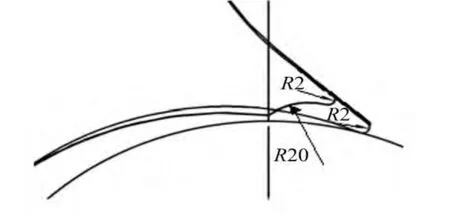
图8 阶梯形隔舌与常规隔舌

叶轮和蜗壳流道内监测点分布图如图4与图5所示。此处仍然选取一级叶轮压力脉动较大的点a1、a4、d1和d2进行对比，优化前后监测点压力脉动对比如图9所示。

图9中实线谱为原模型前监测点压力脉动，虚线谱为采用阶梯隔舌监测点压力脉动。从图中可以看出监测点a1效果比较好，而监测点a4压力脉动虽然小幅降低，甚至有些频率幅值略有升高，但整体还是有一定改善效果。造成这种情况的原因是监测点a1更接近隔舌区，而优化后隔舌区射流及回流现象有明显改善，所以效果较好，而监测点a4则距离隔舌区较远，改善效果不是很明显。而监测点d1和d2都靠近隔舌区，从图9可以看出监测点d1和d2改善效果都比较理想。总体来看阶梯隔舌对整体流场的压力脉动有很明显的改善效果。

2.2.2 优化隔舌前后流场激励力对比

将优化前后的叶轮所受流场激励力进行对比，对比结果如图10所示。

图中实谱线为原模型流场激励力，虚谱线为采用阶梯隔舌后叶轮的流场激励力。以一级叶轮受力对比为例，从图10可以看出，优化隔舌后流体激励力在一级叶轮叶频下幅值都有一定减小，与优化叶轮相比效果基本相当。可见阶梯隔舌对流场也有一定改善效果。

3 优化效果验证

阶梯隔舌工艺上难于实现，因此实际工程中采用切割叶轮的优化方法。为验证仿真结果，下面进行实验验证。

由于实际测试条件限制，压力脉动、流场激励力测试困难，难于实现。切割叶轮能有效改善压力脉动和流场激励，即多级离心泵的激励源发生了变化，机脚响应会发生相应改变，因此测试切割叶轮前后离心泵的机脚响应来间接验证优化效果。离心泵机脚考核点布置图如图11所示。优化前后各考核点的加速度响应对比如图12所示。

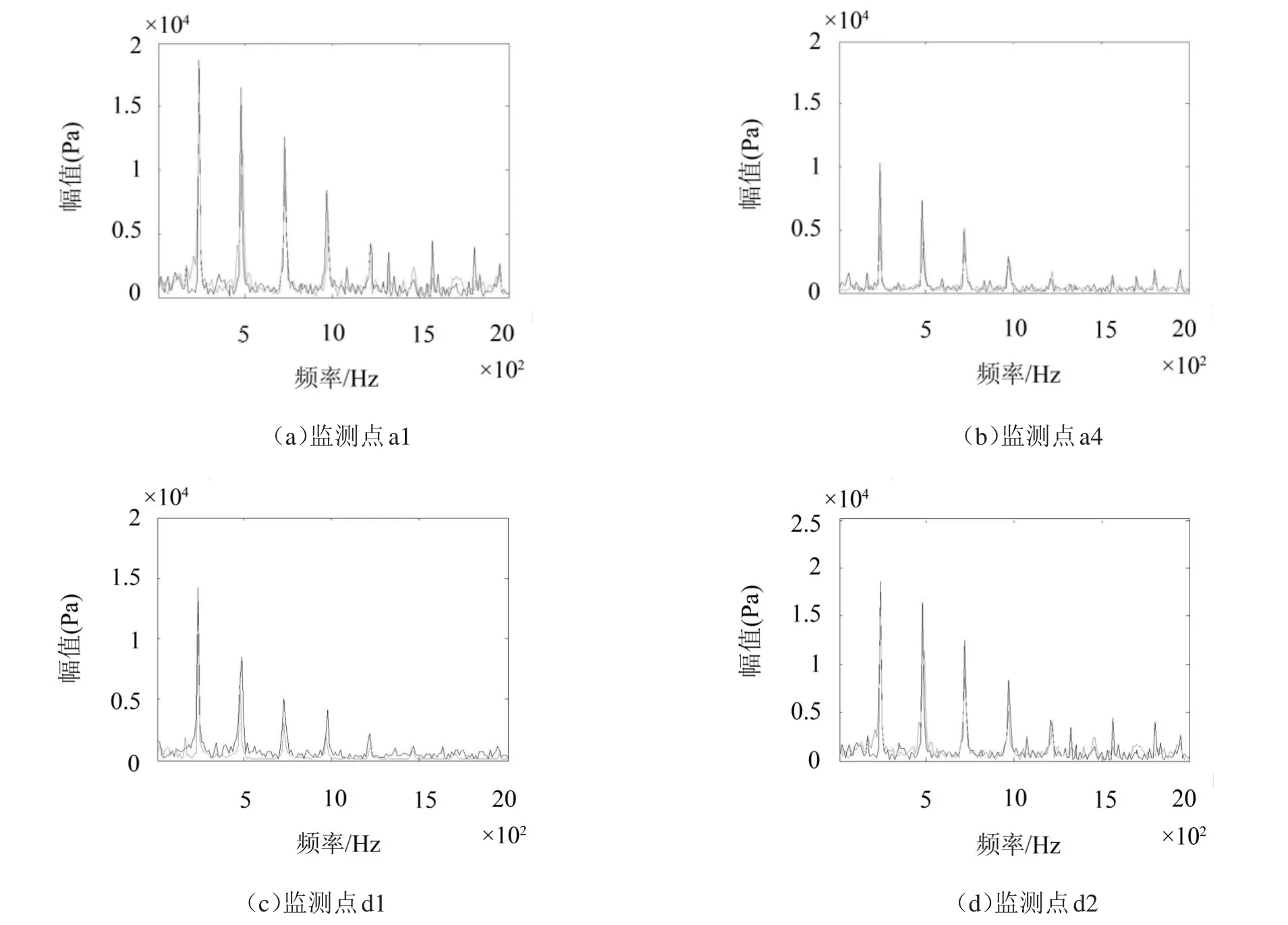
图9 各监测点压力脉动对比

表2 响应对比

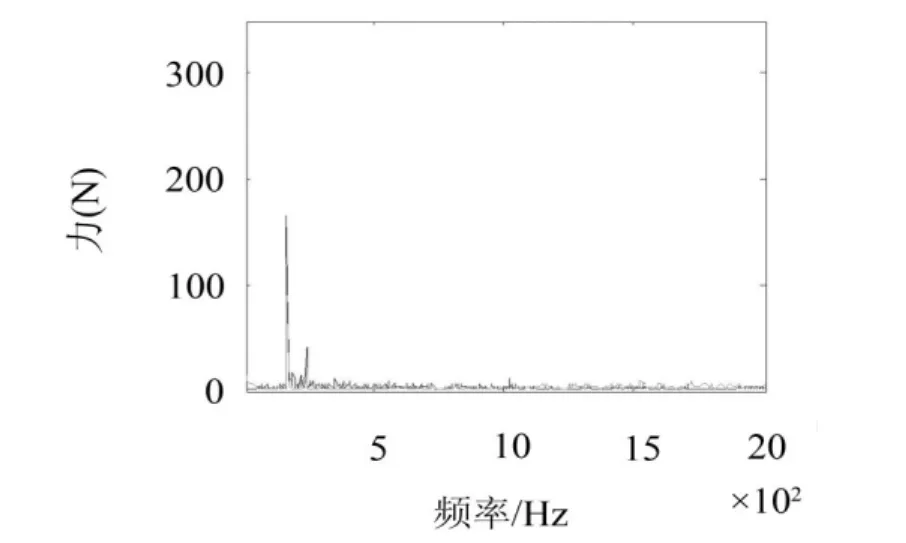
图10 一级叶轮z向力

从图12中可以看出优化后各级叶轮叶频（171 Hz、242 Hz）下响应有所降低，可见切割叶轮有一定改善效果。表2对比了优化前后各考核点的加速度振级。从表2可以看出优化后总振级降低了4 dB左右，由此可以间接验证流场的优化是有一定改善效果的。

4 结语

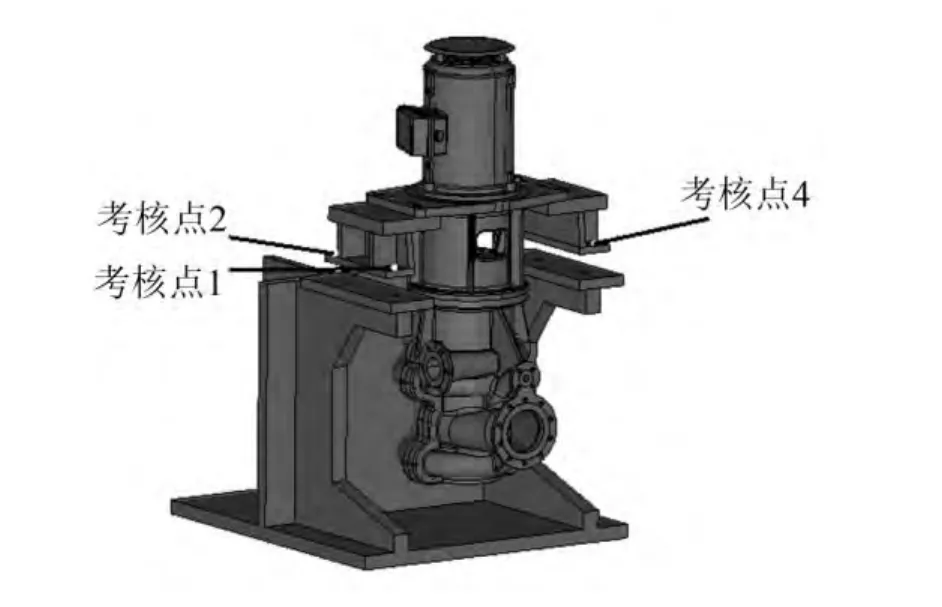
图11 考核点布置图

(1)选用切割叶轮和改用阶梯隔舌方法对流场优化，从压力脉动及叶轮受力两个方面对优化效果进行对比，发现监测点压力脉动有所降低，并且叶轮受力也有所减小；

(2)通过测试机脚响应的变化对优化效果进行间接实验验证，采用切割叶轮的方法总振级降低了4 dB左右，可见优化对流场有一定的改善效果。

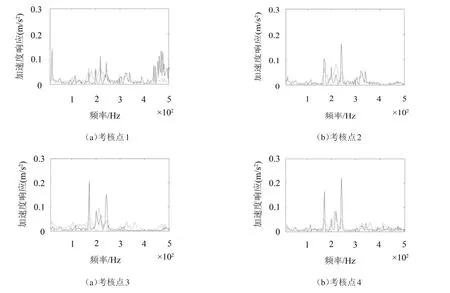
图12 考核点响应

[1]蒋爱华.流体激励诱发离心泵基座振动的研究[D].上海：上海交通大学，2011.

[2]Chu S,Dong R,Katz J.Relationship between unsteady flow,pressure fluctuation,and noise in a centrifugal pump—Part A:use of PIV data to compute the pressure field[J].ASME J.Fluids Eng.,1995,117：24-29.

[3]Gonzalez J,Fernandez J,Blanco E,et al.Numerical simulation of the dynamic effects due to impeller-volute interaction in a centrifugal pump[J].ASME J.Fluids Eng.,2002,124:348-355.

[4]Majid K.Numerical study of unsteady flow in a centrifugal pump[J].Journal of Turbomachinery,2005,127:363-371.

[5]朱荣生，胡自强，杨爱玲.双叶片泵内非定常流动的数值模拟[J].排灌机械工程学报，2011，29(1)：66-68.

[6]倪永燕.离心泵非稳态湍流场计算及流体诱导振动研究[D].镇江：江苏大学，2008：10-30.

[7]Gonzalez J,Fernandez J,Blanco E,and et al.Numerical simulation of the dynamic effects due to impeller-volute interaction in a centrifugal pump[J].ASME J.Fluids Eng.,2002,124:348-355.

[8]Gonzalez J.,Carlos Santolaria,Unsteady flow structure and global variables in a centrifugal pump[J].ASME J.Fluids Eng.,2006,128(9):937-946.

[9]Gonzalez,J.,Parrondo,J.,Santolaria,C.,and Blanco,E.,Steady and unsteady radial forces for a centrifugal pump with impeller to tongue gap variation[J].ASME J.FluidsEng.,2006,128:454-462.

[10]Sudo,Komatsu T,Kondo.Pumping plant noise reduction[J].Hitachi Rev.,1980,29(5):217.

[11]关醒凡.现代泵技术手册[M].北京：北京宇航出版社，1998：10-30.

[12]祝磊，袁寿其，袁建平.阶梯隔舌对离心泵压力脉动和径向力影响的数值研究[C].国际农业工程大会论文集.江苏大学流体机械工程技术研究中心，2010：115-121.