自适应模糊小波滑模控制在交流伺服系统中的应用

侯润民，刘荣忠，侯远龙，高强，杨国来

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

某武器系统在不同装弹量情况下，其转动惯量变化范围较大，且在该武器发射时，由于在回转部分产生巨大的负载变化和冲击，致使系统存在严重的非线性，因此传统的控制方法很难得到满意的控制效果。滑模变结构控制对系统的摄动和外界扰动具有较强的鲁棒性，并且可通过控制器结构的调整和变化，有效地控制具有参数变化和外部扰动的被控制对象，方法简单易于工程实现，从而为复杂的非线性系统控制问题提供了一种较好的解决方案［1］。

为了获得更好的电机驱动性能，文献［2 -3］提出了终端滑模控制策略，即在滑模面的设计中引入非线性函数，来确保跟踪误差在有限时间内收敛到0. 然而，终端滑模控制在收敛时间上却未必是最优的，其主要原因在于系统状态接近平衡状态时，非线性滑动模态的收敛速度要比线性滑动模态的收敛速度慢。为此，文献［4 -5］提出的快速终端滑模控制使系统状态在有限时间内收敛，突破了普通滑模控制在线性滑模面条件下状态渐进收敛的特点，并且该控制对系统不确定性和干扰具有良好的鲁棒性;然而由于快速终端滑模无切换项，当系统存在参数摄动和外界干扰时，快速终端滑模方法的控制性能将降低。文献［6］采用自构造模糊神经网络快速终端滑模控制策略对永磁同步电机的速度进行了研究;文献［7］基于模糊理论处理未知干扰和不确定因素对系统的影响，研究了自适应模糊控制方法;然而在模糊控制中，由于模糊逻辑控制器的模糊规则并不充足，因此系统的控制性能并不理想。

小波神经网络［8］是在小波分析基础上提出的一种前馈型网络，它将神经网络的结构模型与信号的多分辨和多尺度分析有效地结合起来，使得小波基元及整个网络结构的确定有了可靠的理论依据，从而避免了结构设计上的盲目性;网络权系数的线性分布和学习目标函数的凸性，使网络训练过程有效地避免了局部最优等非线性优化问题。

文献［9］提出了一种基于自适应模糊小波网络的小波多分辨率分析逼近任意非线性函数变换和模糊的概念，但是对系统的鲁棒性没有进行讨论。文献［10］采用自适应模糊小波神经滑模控制对不确定非线性系统进行了研究。将模糊模型引入到小波神经网络的优点是在不增加小波基数量的情况下以提高函数的逼近精度，并且每一个模糊规则所对应的子小波神经网络都是由单尺度小波所组成的。

本文利用自适应模糊小波神经网络控制器(AFWNC)具有以任意精度一致逼近非线性函数的能力，对系统未知干扰和不确定进行估计，并通过自适应PI 控制来提高系统的鲁棒性能，进而与快速终端滑模控制(FTSMC)方法相结合，提出了自适应模糊小波神经网络快速终端滑模控制(AFWNFTSMC)，并采用Lyapunov 方法证明了其稳定性。仿真研究表明，本文给出的控制方法能较好地满足系统的动态和稳态指标的要求。

1 伺服系统数学模型推导

由于本文主要考虑的是由系统负载变化及参数摄动等不确定性所引起的非线性，因此在模型推导中将伺服系统线性化并做如下假设:1)无饱和效应;2)电动机气隙磁场均匀分布，感应反电动势呈正弦波状;3)磁滞及涡流损耗不计;4)转子上无励磁绕阻。图1 为交流伺服系统控制图。图中:θr为目标位置;θ 为实际目标位置;U 为控制电压;Kα为放大器增益;R 为电机电枢回路电阻;TL为负载扰动力矩;Tf为摩擦力矩扰动;J 为折算到电机转子上的总转动惯量;B 为粘性摩擦系数;ωd为电机角速度;i 为减速比;L 为电机电枢回路电感;Kd为电机力矩系数;Td为电机电磁转矩;Ee为电机电枢反电动势;Ce为电机反电动势系数。

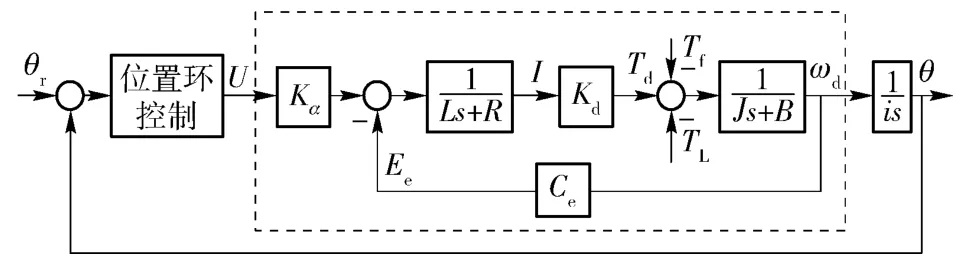
图1 交流伺服系统控制图Fig.1 Control diagram of AC servo system

由于电流环速度远快于速度环和位置环的响应速度，故可将电流环近似简化为一个比例环节［11］。因此，系统的数学模型［12］可写成:

电机电磁转矩为

由转矩平衡方程可得

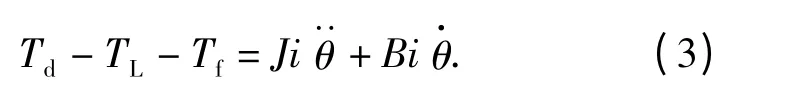
将(2)式代入(3)式可得

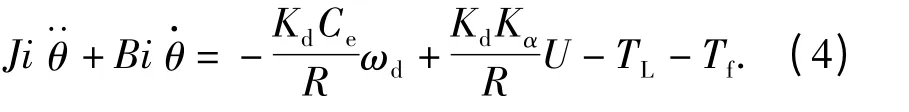
(4)式两边同乘以1/i，并整理得

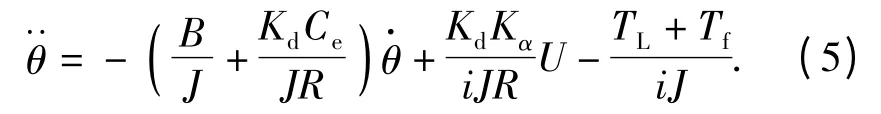
取状态变量为x =［x1x2］T，令x1=θ，x2=ωd=则位置伺服系统的状态空间方程为

2 快速终端滑模控制设计

定义系统的跟踪误差e =xr-x，xr和x 分别为系统的期望输出和实际输出，则快速终端滑模面设计［13］为

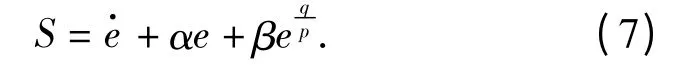
系统的位置控制律设计为

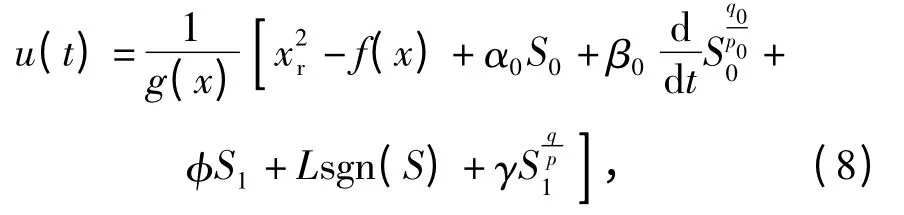
式中:S0=x1;φ，γ ＞0;p 和q 为正奇数，且q ＜p.

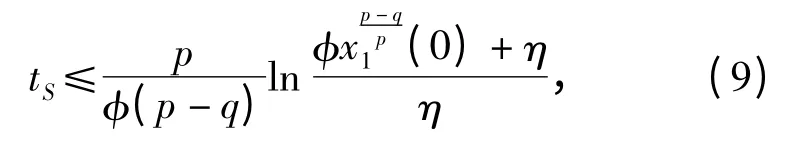
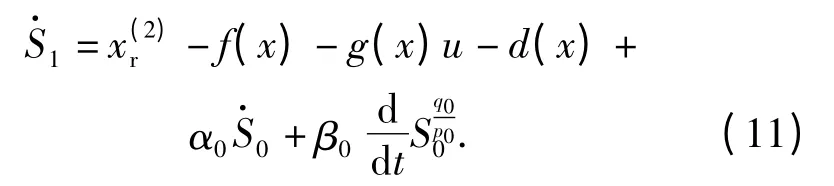
将控制率(8)式代入(11)式，得

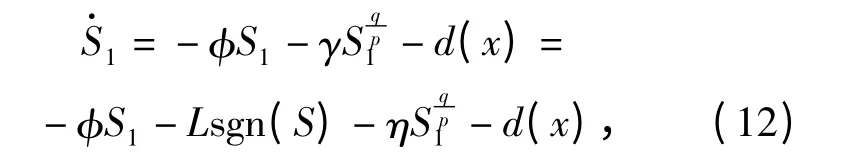
则

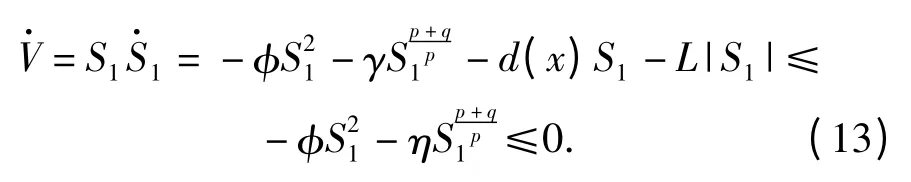
由于p 和q 为正奇数，即p +q 为偶数，因此可以判定系统为稳定系统。

3 自适应模糊小波网络FTSMC 设计

由于f(x)和g(x)在实际系统中常常是未知的，因此FTSMC 算法就很难由(8)式直接得到。针对这一问题，本文利用自适应模糊小波神经网络对未知项进行模糊逼近，实现AFWNC，并且采用自适应PI 控制取代FTSMC，使其连续化，从而有效降低抖动和提高系统的鲁棒性。

3.1 自适应模糊小波神经网络控制器

模糊小波神经网络是由多分辨小波变化和传统的TSK 模糊系统组成的。在模糊小波网络中，每个模糊规则对应于一个由给定的伸缩值小波组成的子小波神经网络。一个典型的模糊小波神经网络被一系列模糊规则描述［10］如下:

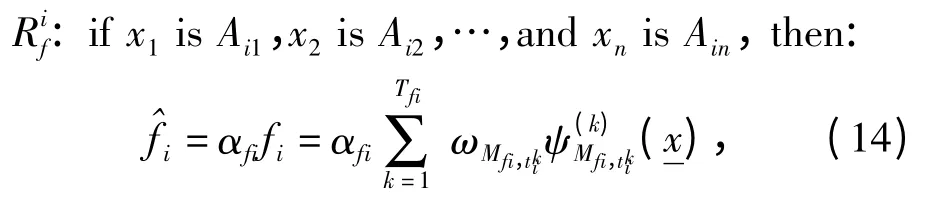
自适应模糊小波神经网络的结构如图2 所示，在图2 中每层的神经元数目分别是n，n×c，c，c+1，权值变量分别为

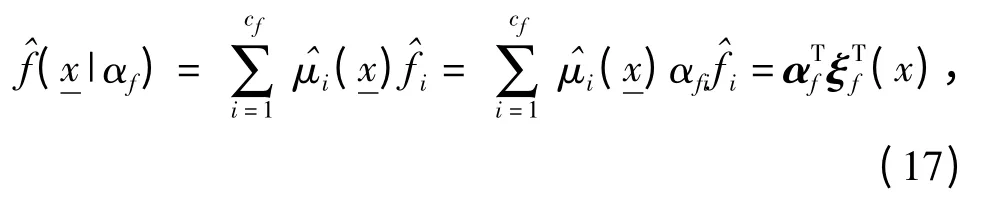
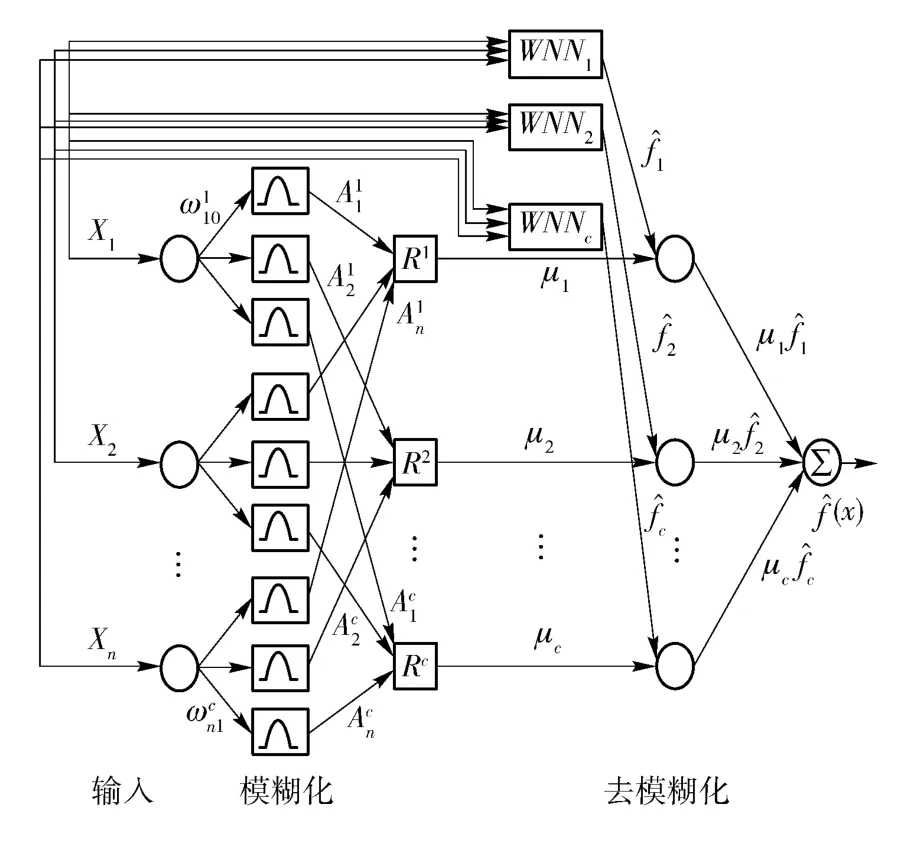
图2 自适应模糊小波神经网络结构图Fig.2 Structure of adaptive fuzzy wavelet neural network

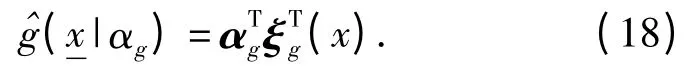
为了使实际输出和期望输出之间的误差最小，在构造模糊小波控制器时，必须先对训练数据进行构造，其表示为

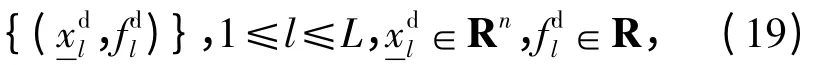
由于本文中选取Mexican hat 小波，因此伸缩参数Mfi选取范围在［-5 4］，并且基于数据构造(19)式，其小波数目［14］

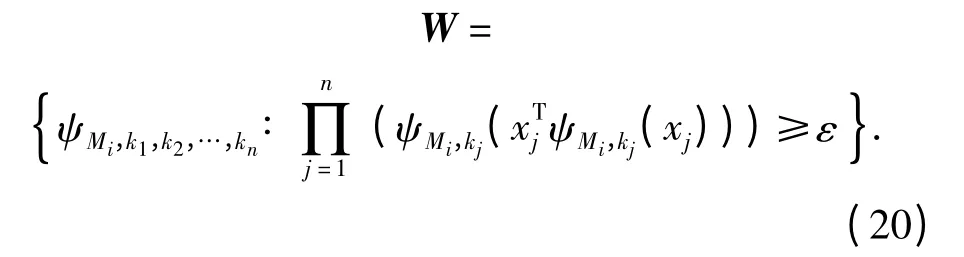
在小波W 中，选用最小正交二乘法［15］(OLS)将训练数据进行帅选。假设N 是运用OLS 算法得到的新的小波数目，因此(14)式中的变量Tfi可变为

图3 模糊小波神经网络算法构造图Fig.3 The algorithm construct of adaptive fuzzy wavelet neural network

式中:i=1，2，…，c;j=1，2，…，n;r=1，2，3.

在完成上述步骤后，本文采用扩展卡尔曼滤波器(EKF)对变量进行学习，并且同时采用最小二乘法(LS)对权值变量ωMi，tki进行更新。根据(19)式，其EKF 算法［14］表示为

式中:

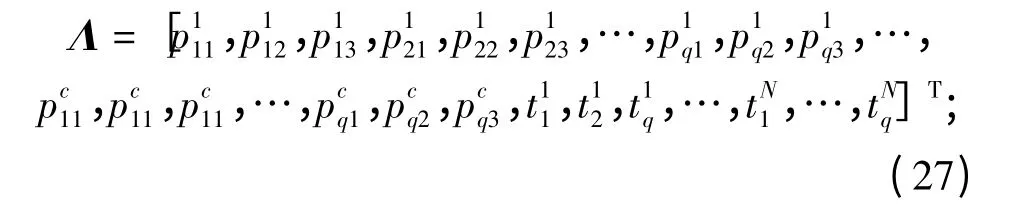
p(l)为误差协方差矩阵;H(l)是Hessian 矩阵，其包含了每一个Λ 中的模型输出的偏导数，表示为

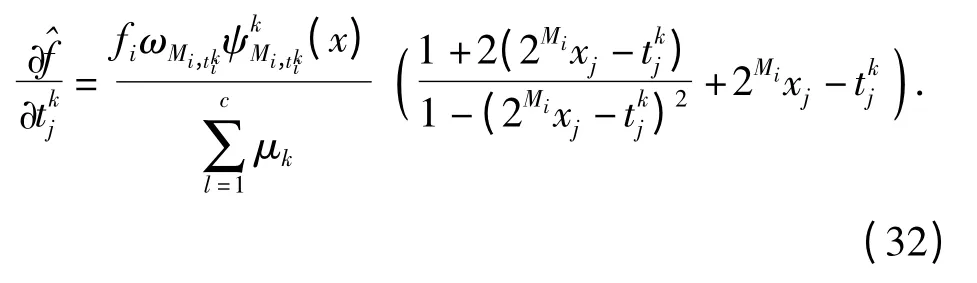
学习算法运用第i 次迭代性能指标函数来判定是否需要继续学习。函数表示为

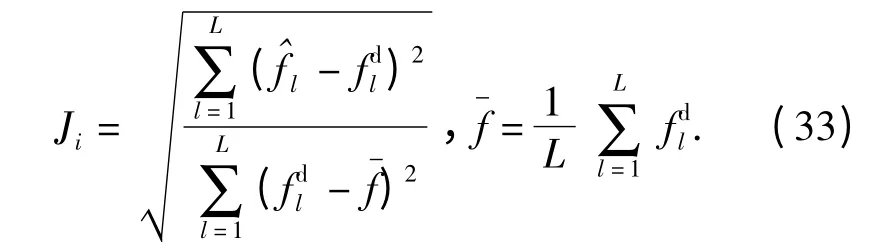
(27)式～(33)式中:j =1，2，…，n;r =1，2，3;k =1，2，…，N;i=1，2，…，c.

3.2 自适应PI 控制

当滑模状态|S|在边界层厚度φ 内，自适应PI控制器［16］表示为

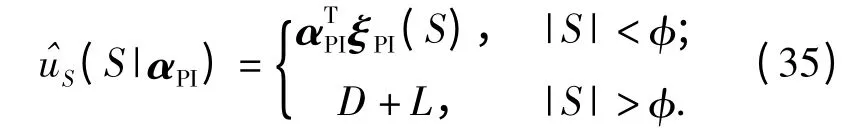
结合上述控制方法，系统的位置控制律表示为

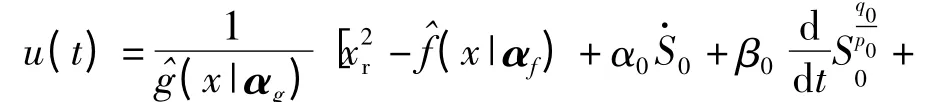
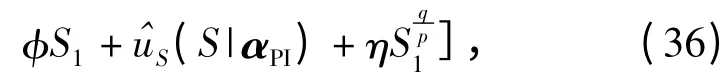
设自适应律为

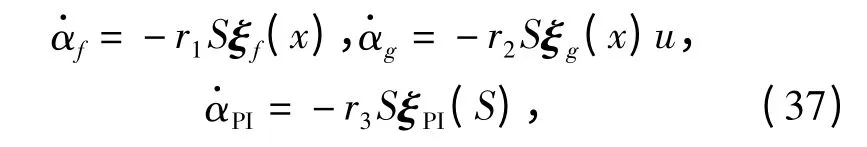
式中:r1、r2、r3＞0. 自适应模糊小波神经网络FTSMC 图为图4 所示。

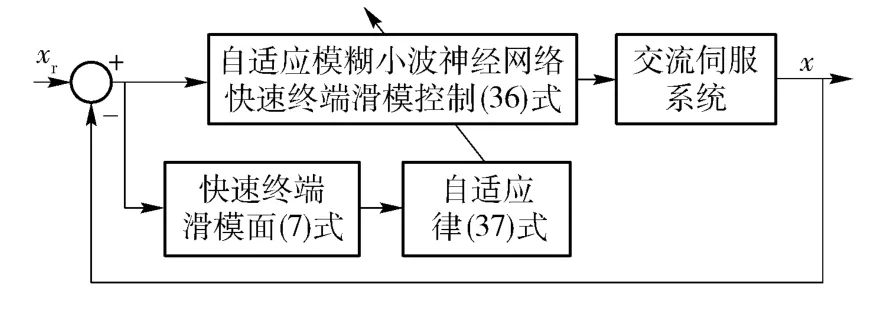
图4 自适应模糊小波神经网络FTSMC 图Fig.4 The control diagram of adaptive fuzzy wavelet neural network FTSMC

证明 定义最优参数为

式中:Ωf、Ωg和ΩPI分别表示αf、αg和αPI的集合。

设最小逼近误差为

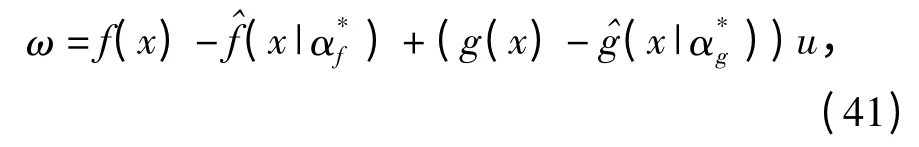
式中:|ω|≤ωmax.

定义Lyapunov 函数:

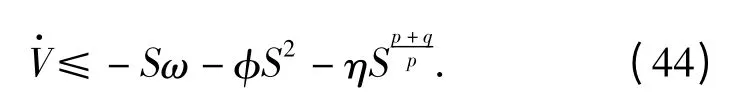
根据模糊小波神经网络逼近理论，自适应模糊小波神经网络系统可实现使逼近误差ω 非常小，因此

4 仿真实验与分析

为了验证本文中自适应模糊小波神经网络快速终端滑模控制器的性能，选取自适应模糊滑模控制器与其进行对比。采用功率为9.7 kW 的交流伺服电动机，其系统的主要参数为:系统负载转动惯量为J =5 675 kg·m2;摩擦力矩为800 N·m;摩擦系数B=1.43 ×10-4N·m/(rad·s-1);减速比i =1 039;系统负载扰动力矩为TL=93.2 ×103N·m;电机反电动势系数Ce=0.195 V/(rad·s-1);电机转矩系数Kd=0.195 N·m/A. 在自适应模糊小波神经控制中取10 个模糊规则，其每个输入变量都被分配了10 个隶属函数，并且选取10 个自调整参数对控制器中的参数进行实时调整。自适应模糊小波神经网络快速终端滑模控制器参数选取:β0=0.2，α0=0.25，η=80，p0=9，φ=100. 系统的位置指令信号取正弦信号。自适应律参数取:r1=4，r2=2，r3=1. 设自调整参数的初始值为取系统的初始状态x0=［π/6，0］，L =2. 仿真结果如图5 ～图9 所示。

图5 为在2 s 时加入一个500 N·m 阶跃扰动的位置响应曲线。从图5 可以看出，当负载出现扰动时，采用AFWNC 算法的位置响应出现较大的偏移，并且需要0.6 s 才能恢复到目标位置;而采用AFWN-FTSMC 算法时，系统具有较强的抗干扰能力，对系统负载扰动不敏感，具有较强的鲁棒性，且只需0.12 s 就能达到目标位置。

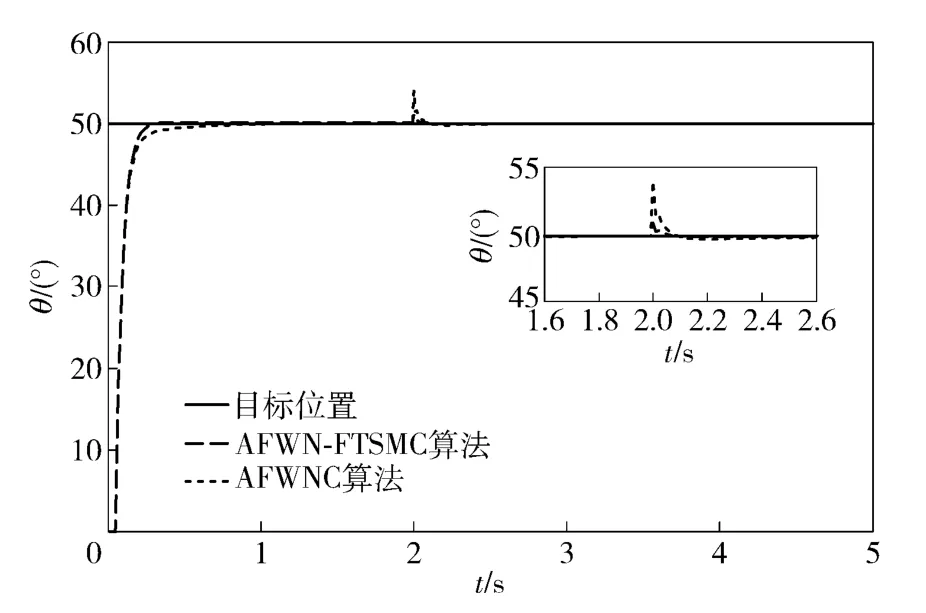
图5 负载扰动时的阶跃响应曲线Fig.5 Step response curve under load disturbance

图6为初始转动惯量J =5 675 kg·m2时的位置响应曲线;图7 为系统转动惯量变化到1.5 倍初始转动惯量时的位置响应曲线。从两图可以看出，采用自适应模糊滑模控制时系统产生了超调，且系统到达稳态时所需要的时间分别为2.10 s 和3.60 s;而采用AFWN-FTSMC 时，系统响应时间变快，达到稳态时所需要的时间分别为0.37 s 和0.96 s，且系统对参数的变化具有更好的抑制性能。

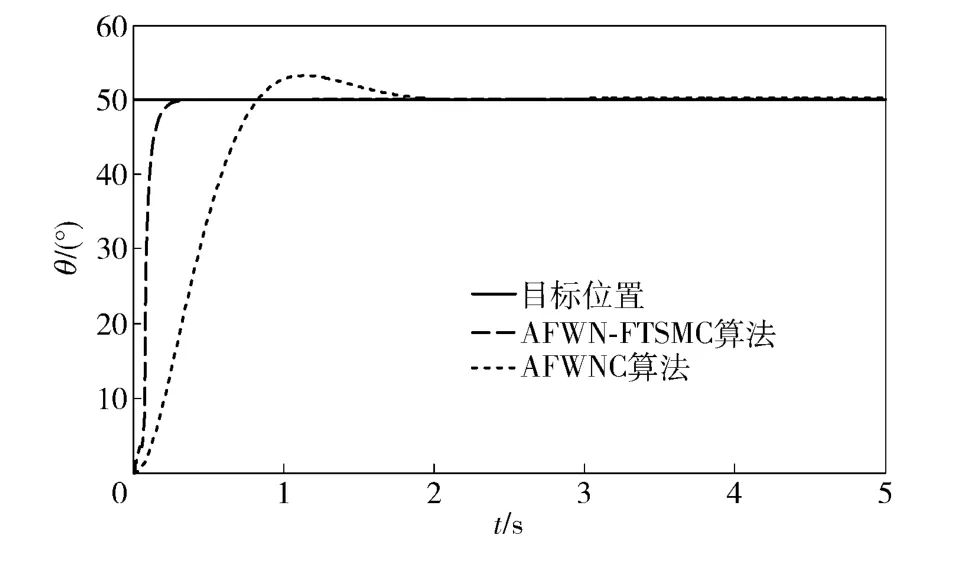
图6 初始转动惯量的阶跃响应曲线Fig.6 The initial moment of inertia of step response curves

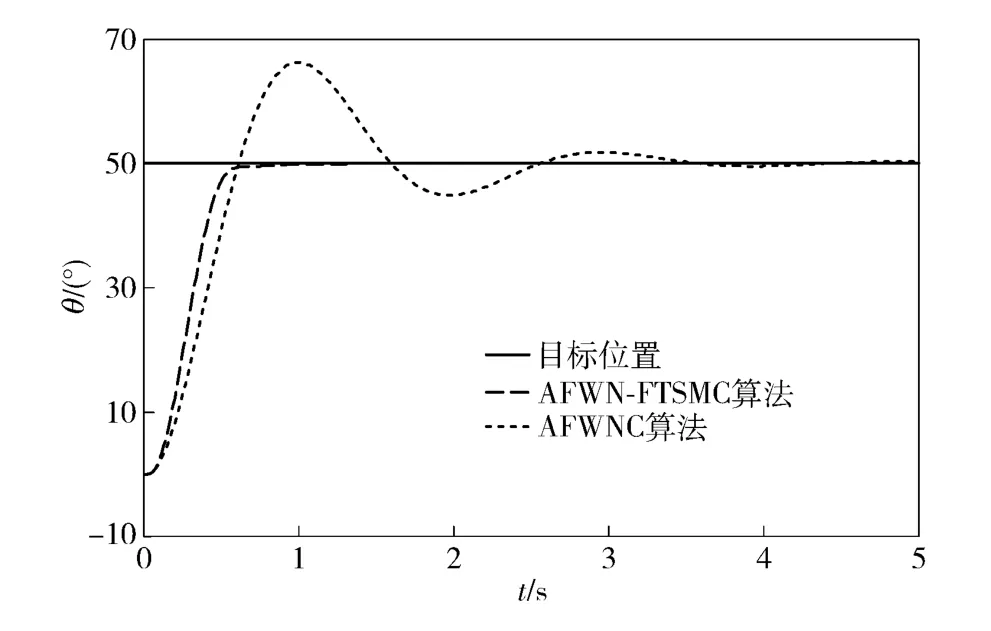
图7 转动惯量变化到1.5 倍初始转动惯量时的阶跃响应曲线Fig.7 Step response curves for moment of inertia be changed by a factor of 1.5 times

系统的控制信号曲线和系统的正弦跟踪误差曲线如图8 和图9 所示:采用AFWN-FTSMC 时，系统的控制曲线明显比用AFWNC 的曲线平滑。这是因为引入AFWNC 和自适应PI 控制后，能有效地逼近快速终端滑模控制器的未知参数，将其连续化，从而能够有效地降低抖动;并且在AFWN-FTSMC 下，系统具有较好的稳态控制精度。

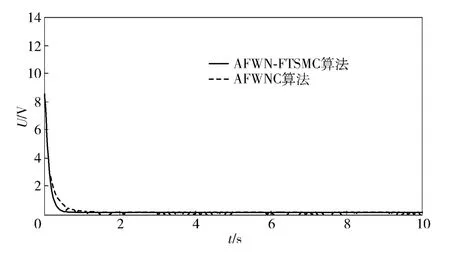
图8 系统的控制输入信号曲线Fig.8 Control input signal curves of system

图9 系统的正弦跟踪误差曲线Fig.9 Sinusoidal tracking error curves of system

5 结论

本文针对某武器大功率交流伺服系统，提出了一种AFWN-FTSMC 方法。仿真实验结果表明，该方法对系统的不确定性和外界干扰具有较强的鲁棒性和较好的动态及稳态响应性能，并且能有效削弱控制信号中的抖动。

References)

［1］Park D W，Choi S B. Moving sliding for high-order variable structure systems［J］. Int J Control，1999，72 (11):760 -970.

［2］Wu Y，Man Z. Terminal sliding mode control design for uncertain dynamic systems［J］. Systems ＆ Control Letters，1998，34(5):281 -287.

［3］Park K B，Lee J. Comments on a robust MIMO terminal sliding mode control scheme for rigid robot manipulators［J］. IEEE Trans Automatic Control，1996，41(5):761 -762.

［4］Huang Y S，Sung C C. Implementation of a fast terminal sliding mode controller for direct thrust control systems［J］. Theory and Applications IET，2010，4(3):326 -338.

［5］Yu S H，Guo G. Global fast terminal sliding mode control for robotic manipulators［J］. International Journal of Modeling Identification and Control，2006，1(1):72 -79.

［6］Lin F J，Su K H. Self-constructing fuzzy neural network speed controller for permanent-magnet synchronous motor drive［J］.IEEE Transactions on Fuzzy System，2001，9(5):751 -759.

［7］Kim E. A fuzzy disturbance observer and its application to control［J］. IEEE Transactions on Fuzzy Systems，2002，10 (1):77 -84.

［8］Zhang Q H，Benveniste A. Wavelet neural［J］. IEEE Transactions on Neural Networks，1992，3(6):889 -989.

［9］Zekri M，Sadri S，Sheikholeslam F. Adaptive fuzzy wavelet network control design for nonlinear systems［J］. Fuzzy Sets and Systems，2008，159(20):2668 -2695.

［10］Kahkeshi M S，Sheikholeslam F，Zekri M. Design of adaptive fuzzy wavelet neural sliding mode controller for uncertain nonlinear systems［J］. ISA Transactions，2013，52(3):342 -350.

［11］郭亚军，王晓锋，马大为，等.自适应反演滑模控制在火箭炮交流伺服系统中的应用［J］. 兵工学报，2011，32(4):493 -497.GUO Ya-jun，WANG Xiao-feng，MA Da-wei，et al. Application of adaptive back-stepping sliding mode control in alternative current servo system of rocket gun［J］. Acta Armamentarii，2011，32(4):493 -497. (in Chinese)

［12］Gao Q，Sun Z，Yang G L，et al. Novel active disturbance rejection-based control strategy for a gun control system［J］. Journal of Mechanical Science and Technology，2012，26(12):4141 -4148.

［13］张伟，孙秀霞，秦硕，等. 自适应模糊全局快速Terminal 滑模控制方法［J］. 计算机工程与应用，2009，45(27):228 -230.ZHANG Wei，SUN Xiu-xia，QIN Shuo，et al. Adaptive fuzzy global fast terminal sliding mode control method［J］. Computer Engineering and Applications，2009，45(27):228 -230. (in Chinese)

［14］Daniel W C H，ZHANG Ping-An，XU Jin-hua. Fuzzy wavelet networks for function learning［J］. IEEE Transactions on Fuzzy Systems，2001，9(1):200 -211.

［15］ZHANG Qing-hua. Using wavelet networks in nonparametric estimation［J］. IEEE Transactions on Neural Networks，1997，8(2):227 -236.

［16］Ho H F，Wong Y K，Rad A B. Adaptive fuzzy sliding mode control design:Lyapunov approach［C］//Proceeding of the 5th Asian Control Conference. Melbourne，Australia:University of Melbourne，2004:1502 -1507.