低冲量质量块冲击下固支泡沫夹芯梁的动力响应

姜文征，刘颖

(北京交通大学 土木建筑工程学院 力学系，北京100044)

0 引言

由于良好的能量吸收能力，泡沫材料及结构被广泛应用于航空航天飞行器、高速轨道车辆、汽车、舰船等重要设施的能量吸收结构的设计中。作为一种典型的夹芯结构，如何预测三明治梁在不同工况下的动力响应是当今泡沫材料及其结构设计的的前沿课题之一。

Fleck 等［1］将三明治梁的结构响应分为3 个阶段，即流固耦合相互作用阶段、芯材压缩阶段以及梁的弯曲和拉伸阶段，建立了爆炸载荷作用下三明治梁的动力响应理论框架。同期，Xue 等［2］通过三维有限元模拟，比较在爆炸载荷作用下，相同质量的单梁和三明治梁的动力响应，发现三明治梁的承载能力高于等质量的单梁;Rabczwk 等［3］和Liang 等［4］通过模拟发现，在爆炸载荷作用下，Fleck 等［1］的模型可能高估或低估三明治梁中点的挠度值。这可能和面板及芯材间的耦合作用机制有关。为了说明和Rabczwk 等［3］计算结果的差别，Deshpande 等［5］讨论了流固耦合相互作用阶段以及芯材压缩阶段三明治梁的耦合响应。他们的分析结果表明，对于高强度芯材的三明治梁，使用Taylor［6］分析方法，透射动量可能被低估20% ～40%. 这解释了Rabczwk 等［3］的计算结果和Deshpande 等［5］模型之间的差别。为了说明和Liang 等［4］计算结果的差别，Tilbrook 等［7］建立了基于响应时间尺度以及三明治梁拉伸/弯曲变形的分析模型。他们的模型中定义了4 种变形过程:三明治芯材部分或全部致密化解耦响应;三明治芯材部分或完全致密化的耦合响应。但是在他们的模型中有一个重要的假设，即在前后面板速度达到一致前忽略芯材剪切强度。因此在前后面板达到一致前，三明治梁被简化为一个压力空腔。很明显，这与实际的泡沫夹芯结构的变形机制是不同的。随后，Qin 等［8-9］和Wang 等［10］做了一系列的理论和实验研究工作。但是他们的工作都是从整体上对梁进行分析，没有考虑梁与芯材的耦合作用。

基于以上讨论，为了更加合理地计及芯材在三明治梁变形过程中的作用，本文在Tilbrook 等［7］的三明治梁模型基础上，提出一个改进的三明治梁模型。在三明治梁变形的第一及第二阶段考虑了泡沫芯材的弯曲作用。基于此模型，研究了低冲量质量块冲击泡沫固支夹心梁的动态响应特性，并与已知实验和数值算例进行了对比，发现当芯材发生整体弯曲变形时，改进模型能够更准确地预测梁的变形。

1 质量块冲击三明治梁分析模型

如图1(a)所示，长2L 的两端固支三明治梁在跨中点处受到以初速v0运动的质量块m0撞击。三明治梁由厚度分别为hf和hb的面板以及厚度为C的芯材组成。在分析过程中，假设面板满足理想刚塑性模型，屈服强度为σy. 梁只在初始轴线方向发生横向位移。考虑小变形情况，即假设中点挠度w与梁的长度相比为小值。因为是小冲量质量块冲击，因此假设芯材在冲击过程中发生均匀变形，并满足图2 所示的应力-应变曲线。基于以上假设，三明治梁可简化为图1(b)所示模型。泡沫芯材被简化为完全刚塑性弹簧，刚塑性弹簧的响应满足图2所示的应力-应变曲线(平台——虚线)。弹簧连接上梁和下梁，计算时，上梁和下梁采用刚塑性模型。考虑泡沫芯材的质量，采用集中质量近似原则，上梁和下梁每单位长度质量分别为

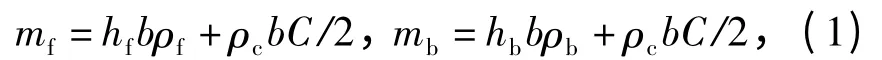
式中:hf、hb和C 分别表示上、下梁及芯材的厚度;ρf、ρb和ρc分别表示上、下梁及芯材的密度;b 为梁的宽度。

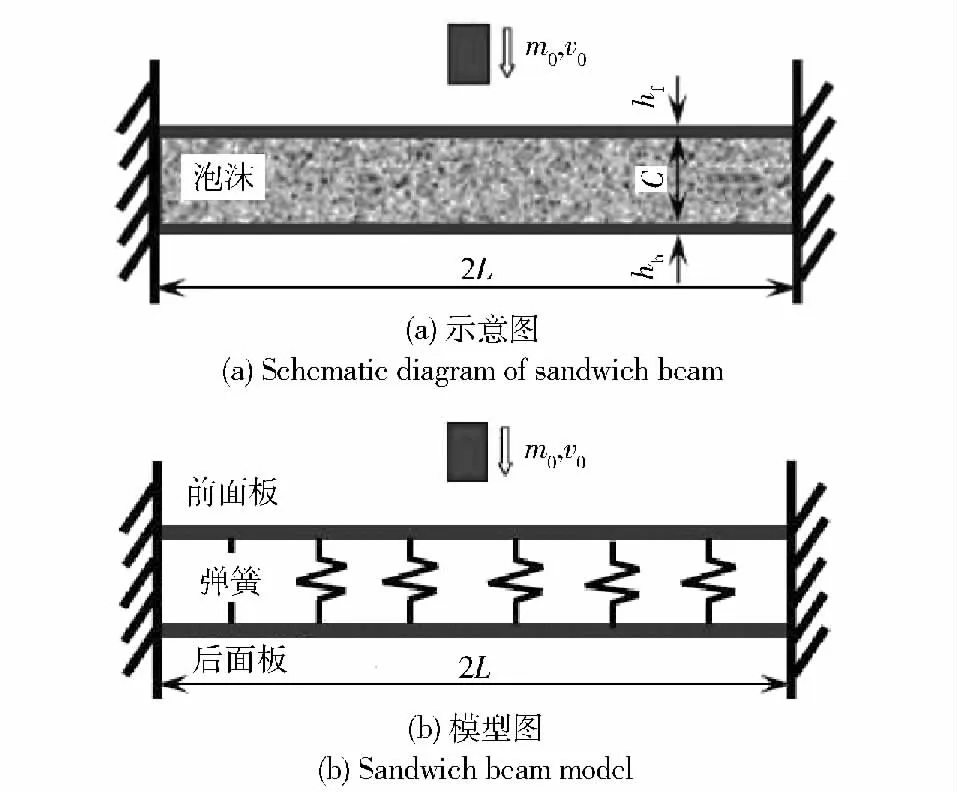
图1 固支三明治梁受以初始速度v0和质量m0的质量块冲击Fig.1 A sandwich beam impacted by a mass

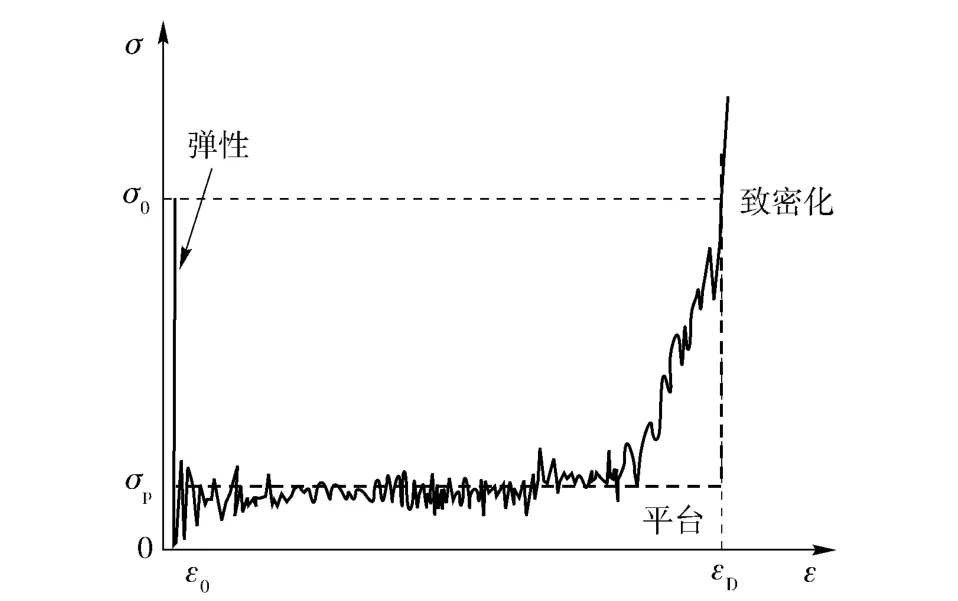
图2 典型泡沫芯材的应力-应变曲线Fig.2 Typical dynamic stress-strain curves of foam

因为在第一和第二阶段变形过程中，芯材除了产生对上梁和下梁的压力外，还会影响梁的整体弯曲性能。同样，把芯材的弯矩平均分配到上梁和下梁以计及芯材的弯曲变形，即

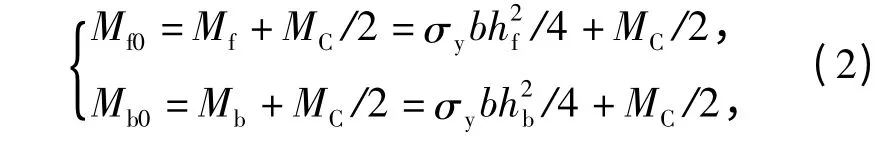
式中:Mf、Mb和MC分别表示上梁和下梁以及芯材的弯矩，

式中:σyC表示泡沫材料的屈服强度;εm= |wf+wb|/C表示中点的压缩应变;wf和wb分别表示上梁和下梁的中点挠度。

基于Jones［11］，设γ=σp/σbs，其中σp为芯材对梁的横向压力，σbs=4Mb0/L2为简化模型下梁的静态极限压力，将芯材分为中等强度芯材(1≤γ≤3)和低强度芯材(γ ＜1). 本文主要讨论中等强度芯材三明治梁的变形过程。

梁的跨中点在冲击瞬时以初速v0运动，而梁的其余部分则处于静止。为了保持动平衡，一个扰动从跨中点向固定端传播。假定撞击物始终保持与梁相接触。整个过程可以分为3 个不同的运动相。运动第一相:一个塑性铰在t =0 时在撞击点产生，并分别从跨中点向两个固定端传播。当塑性铰传播到固定端时，第一相结束。如果芯材达到致密化，直接进入第三相;运动第二相:当上梁的速度比下梁速度大时，上梁继续减速，而下梁继续加速，直到达到共同速度，或芯材达到致密化，第二相终止;运动第三相:三明治梁发生整体变形，以共同速度减速，直至梁和撞击物静止为止。剩余动能全部耗散于位于两个固定端和中点的驻定塑性铰中。

1.1 运动第一相

由于对称性，取梁的右半跨0 ≤x ≤L. 如图3(a)，建立坐标系，x 沿长度方向，从跨中点开始。横向速度场可以表示为

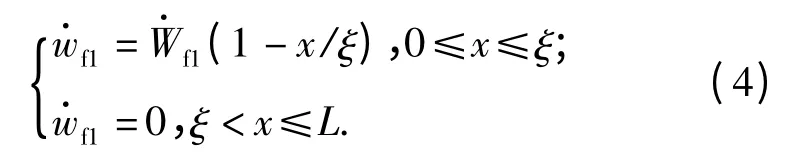
式中:w 为挠度值;ξ 为时间相关的移动塑性铰的位置。由于在塑性铰处(x = ±ξ)，弯矩最大，横向剪力Q=0，考虑梁两动铰中间部分在竖直方向的平衡得

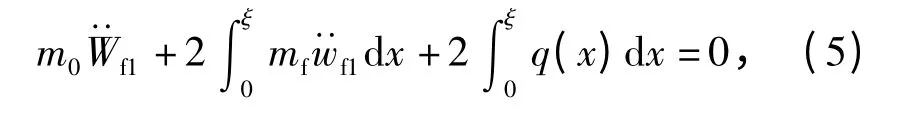
式中:q(x)=σp是芯材作用在上梁上产生的压力，如图2 所示。在发生致密化前压力值保持恒定。

把(4)式代入(5)式整理得

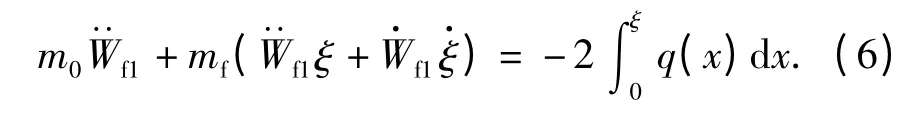
考虑梁在x=0 和x=ξ 处塑性铰之间部分的力矩平衡，以及边界条件，即在x =0 时，Mf1=Mf0;在x=ξ时，Mf1= -Mf0，Q=0 可得

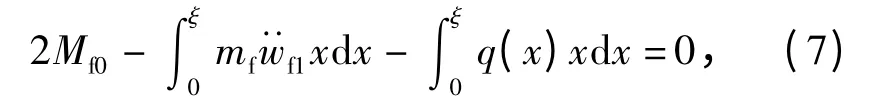
式中:Mf0为上梁截面的极限弯矩。

将(4)式代入(7)式得

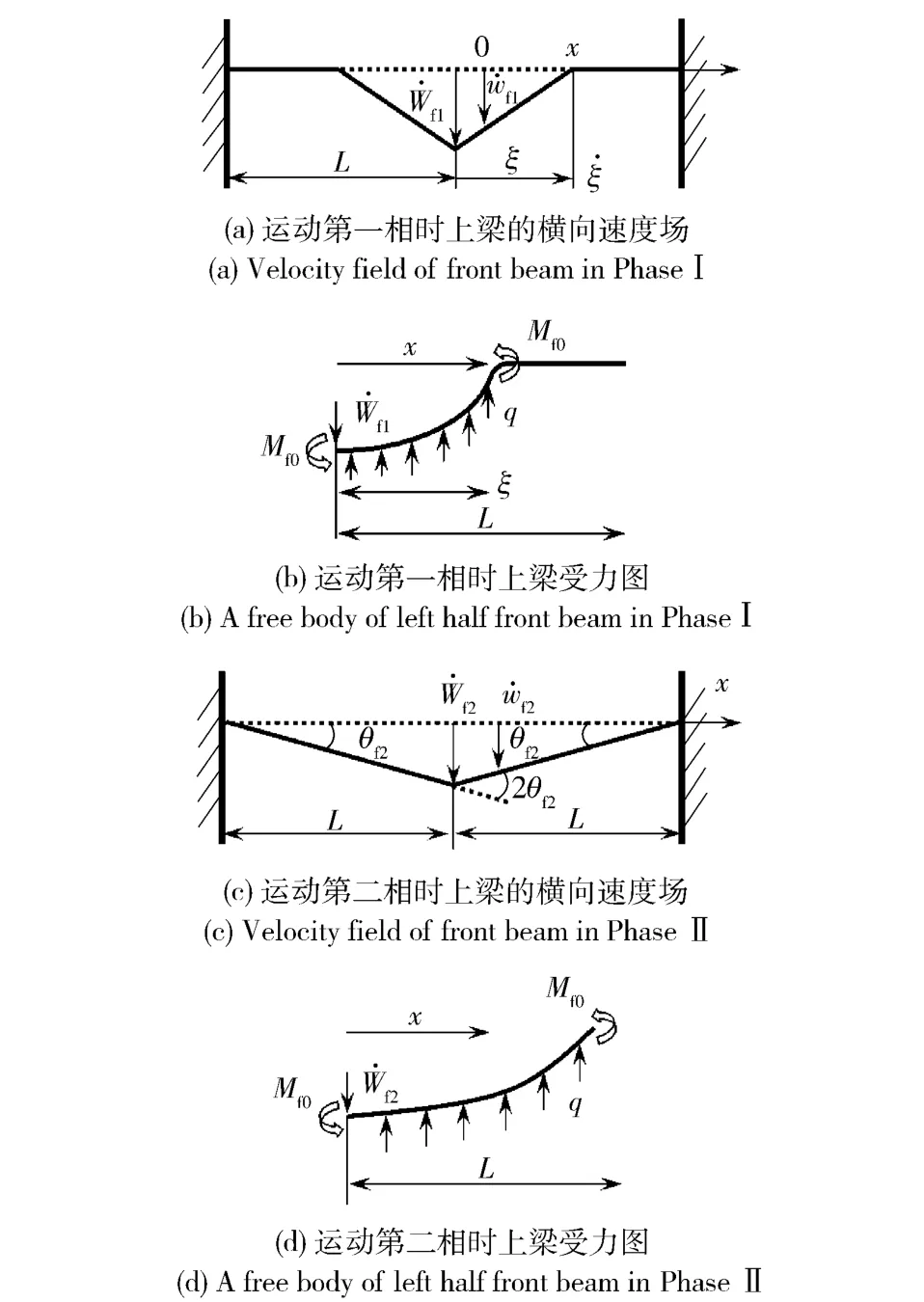
图3 运动第一、第二相时上梁的横向速度场和受力图Fig.3 Velocity field and a free body of left half front beam in Phase Ⅰ，Ⅱ

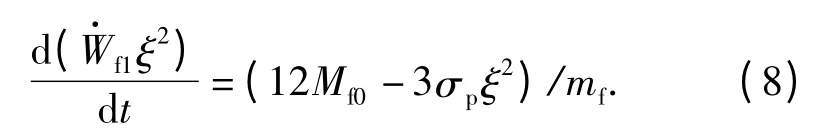
积分(8)式并考虑初始条件t =0，ξ =0，可得移动塑性铰的传播时间

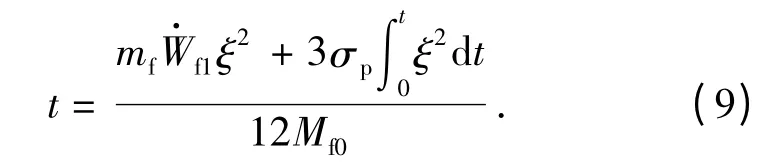
由(6)式得

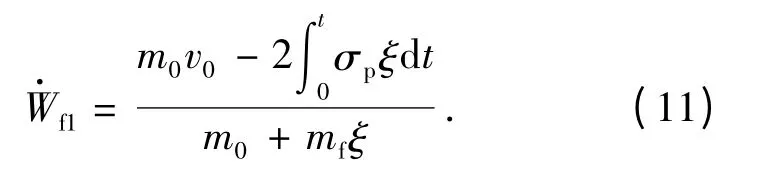
把(11)式代入(9)式整理得

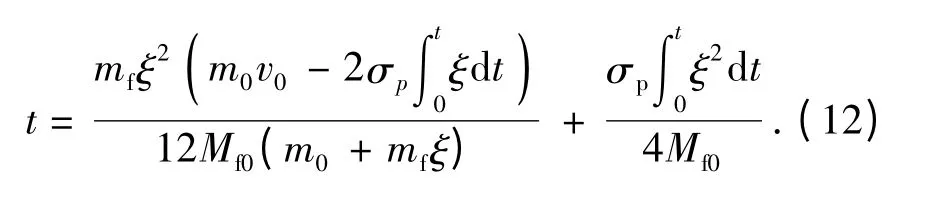
将上式对时间求导，可得移动塑性铰的速度

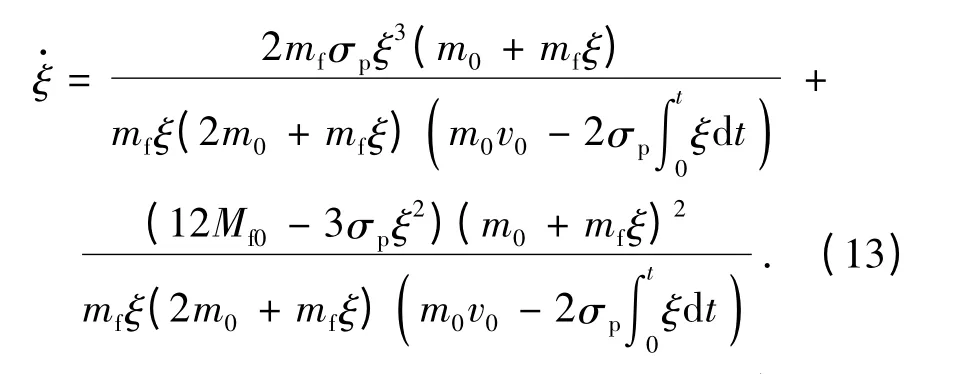
结合相应的初值条件，使用数值方法(龙格库塔方法)对(13)式进行积分，可求得ξ. 将ξ 代入(11)式，积分后可以得到上梁在运动第一相中的挠度。

当σpξ2/4 高于下梁的极限弯距时，下梁也开始变形。如图4(a)所示，假设下梁的横向速度场为

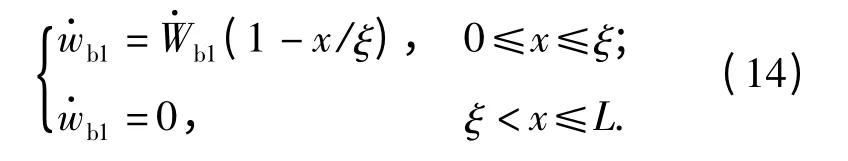
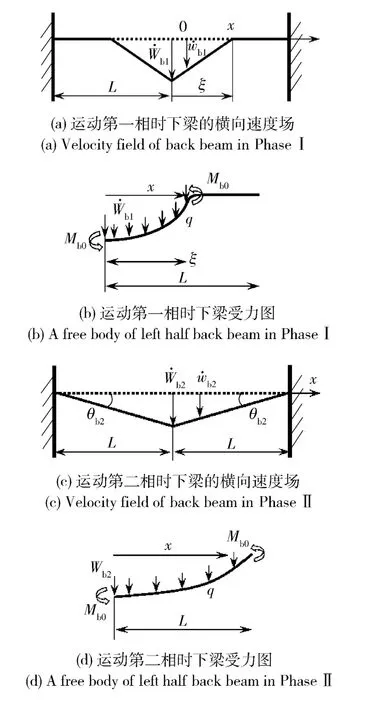
图4 运动第一、第二相时下梁的横向速度场和受力图Fig.4 Velocity field and a free body of left half back beam in Phase Ⅰ，Ⅱ

下梁的控制方程为

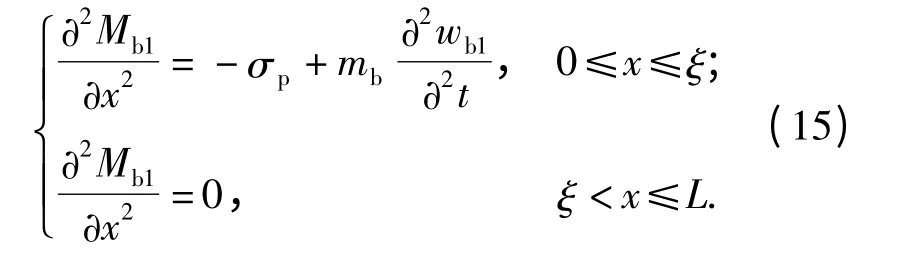
式中:Mb1为下梁的弯矩。

将(14)式代入(15)式得

对(16)式进行积分，由初始条件x =0 时，Q =∂Mb1/∂x=0 和Mb1=Mb0，可得

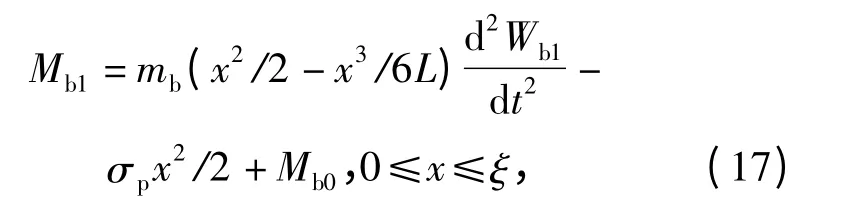
式中:Mb0是下梁的极限弯矩。

因为在x =ξ 时，Mb1= -Mb0，根据(17)式整理得

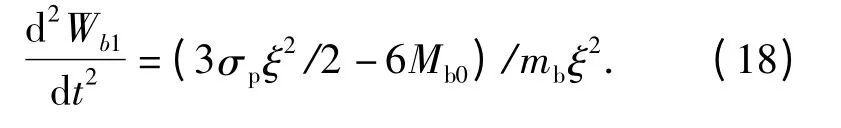
由(18)式可知，当满足3σpξ2/2 -6Mb0＞0 时，下梁才开始运动。由初始条件t =0 时，Wb1==0，(18)式积分得

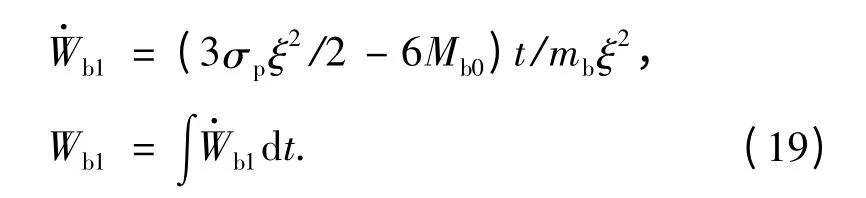
1.2 运动第二相

在运动的第二及第三相，塑性铰固定在支撑端和撞击处，直到整体静止，最终能量全部转化为塑性能。假设在第二相时，上梁的速度场分布为

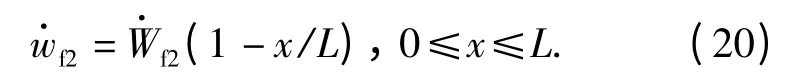
梁的控制方程为

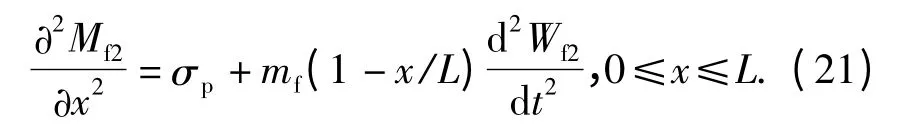
积分(21)式并考虑在x =0 时Mf2=Mf0，Q =/2，以及在x=L 时，Mf2= -Mf0可得

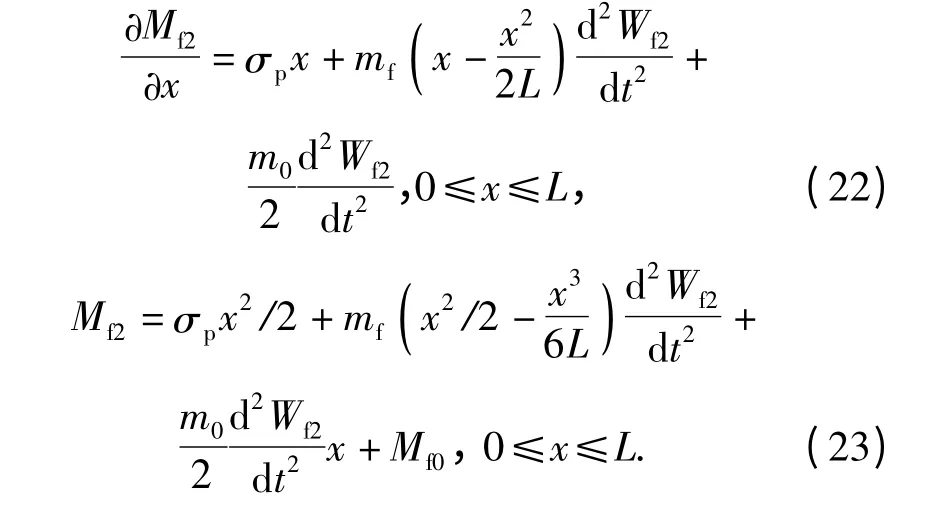
考虑在x=L 时，Mf2= -Mf0，可得

积分(24)式可得上梁中点处速度

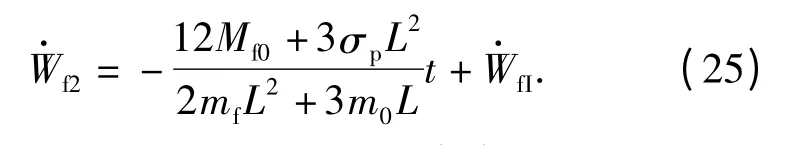
假设下梁的速度分布如图4(c)所示，和上梁速度和加速度推导过程相似，可得下梁中点处的速度和加速度分别为

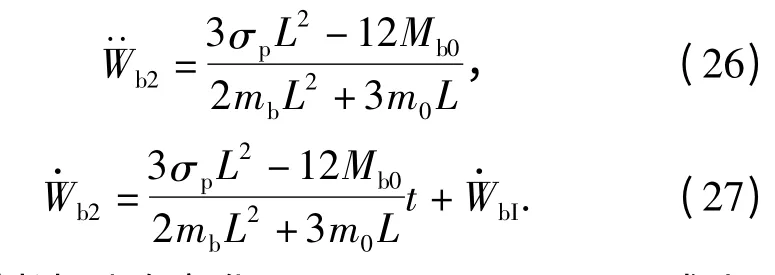
当芯材达到致密化，即|wf+wb|/C ＞εD或上、下梁的速度一致时，第二相结束。

1.3 运动第三相

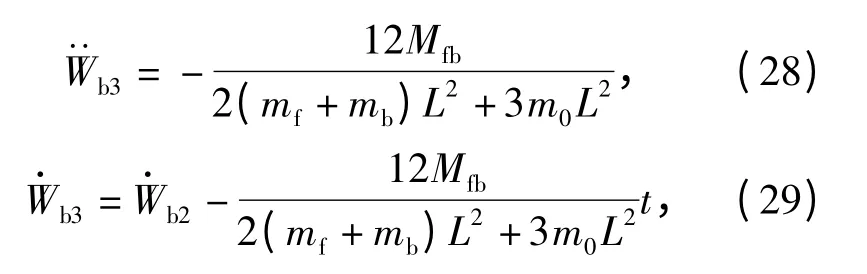
式中:Mfb=Mf0+Mb0.

2 计算结果与讨论

为了验证本文提出的改进模型的可靠性，本文参考Wang 等［10］的实验结果，进行了对比分析。取三明治梁的长度2L=250 mm;梁的宽度b =40 mm;上﹑下面板厚度分别为hf=hb=0.5 mm;芯材厚度C=10 mm;撞击质量m0=0.012 5 kg，质量块几何尺寸与实验尺寸相同。

三明治梁上﹑下面板为铝合金，材料参数为:杨氏模量E=72.4 GPa，剪切模量G =28 GPa，泊松比μ =0.33，密度ρ=2 700 kg/m3，屈服应力σy=75.8 MPa. 芯材的主要材料参数为:杨氏模量E =1.0 GPa，泊松比μ =0.30，密度ρ = 270 kg/m3，屈服应力σy=2 MPa，εD=0.7.

计算中对各参数进行了无量纲化，其中三明治梁几何参数无量纲量分别为

冲量无量纲表示为

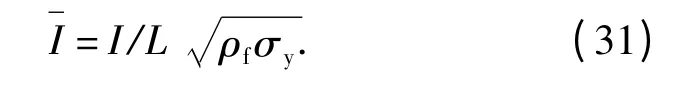
其他无量纲形式为

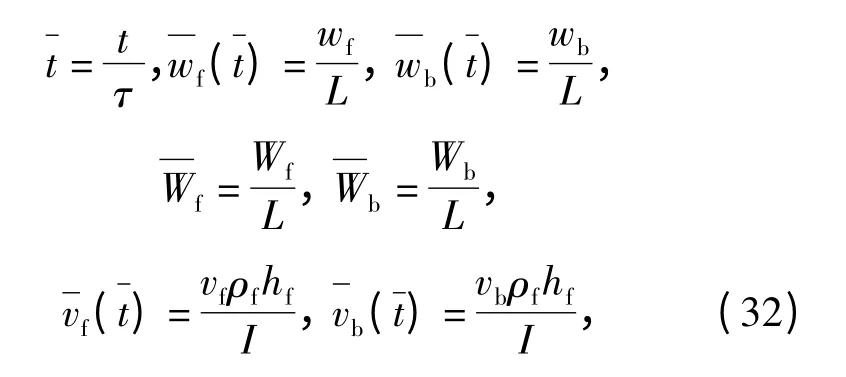
如图5 所示，在小冲量质量作用下，当三明治梁芯材发生整体弯曲变形时，本模型的预测结果与实验结果基本吻合。随着冲击冲量增加，芯材发生剪切或破坏时，本模型预测结果与实验相差较大，这是因为本模型是基于小变形理论，没有考虑膜力的影响。

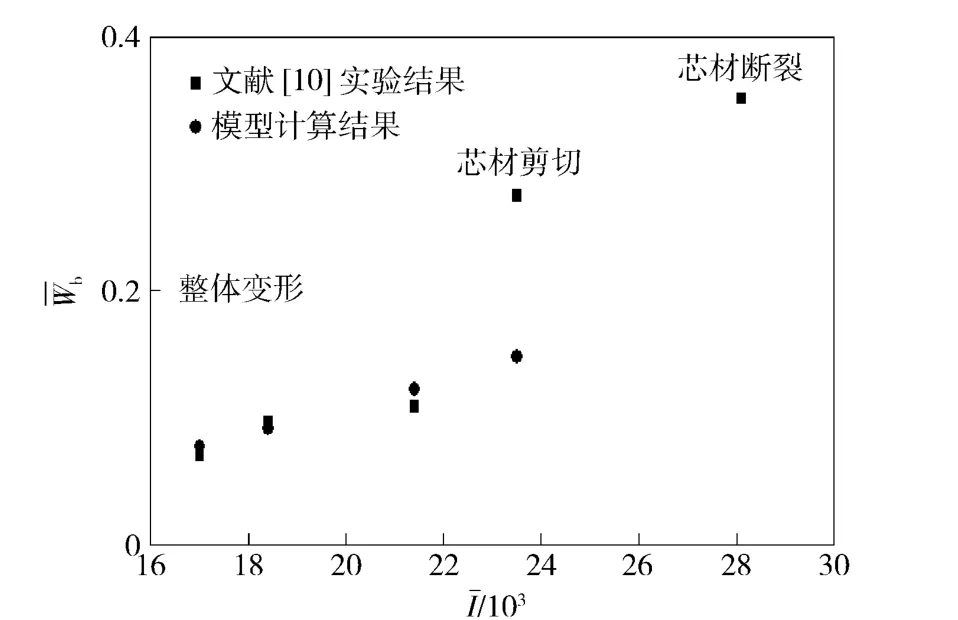
图5 模型计算与已知实验结果对比Fig.5 Comparison of analytical predictions and experimental results

另外，本文基于动力有限元软件LS-DYNA 对冲击块质量为m0=0.012 5 kg，冲击速度为40 m/s 的情况进行了对比计算。计算中选用单元Solid164，面板与芯材完全粘接。面板与芯材分别划分为4 050和10 125 个单元，并优化了撞击处和固定端的网格分布。面板选用各向同性随动强化材料模型，芯材泡沫选用可压扁泡沫模型来近似描述真实泡沫的性质。质量块与夹芯梁之间相互作用，通过DYNA 程序的接触算法实现，这里定义接触类型为面/面自由接触。

图6(a)和图6(b)分别给出了本文的模型、有限元计算结果以及文献［7］模型的预测结果对比。如图6(a)所示，本文模型的预测结果表明在第一相时芯材已发生致密化，此后变形进入第三相，即两面板和芯材以共同速度整体运动，直至速度为0. 本模型的计算结果和有限元计算结果基本吻合。有限元的计算结果并没有明显的芯材致密化进而转入整体变形的过程，这是因为在有限元计算中，只有梁中点处芯材发生致密化，而其他部分并没有致密化。如图6(a)所示，由于文献［7］模型在第一和第二相时把三明治梁近似处理成压力空腔，忽略了芯材的弯曲作用，因此下面板的速度偏高，上下面板在较高的速度达到共同速度，与有限元计算结果偏差较大。如图6(b)所示，其预测的梁的变形偏大。而本文改进的模型和有限元计算结果基本吻合。另外，图6(a)和图6(b)的有限元模拟结果显示下面板与上面板相比延时启动。本文提出的计算模型可以反映这种延时，而且二者比较吻合。

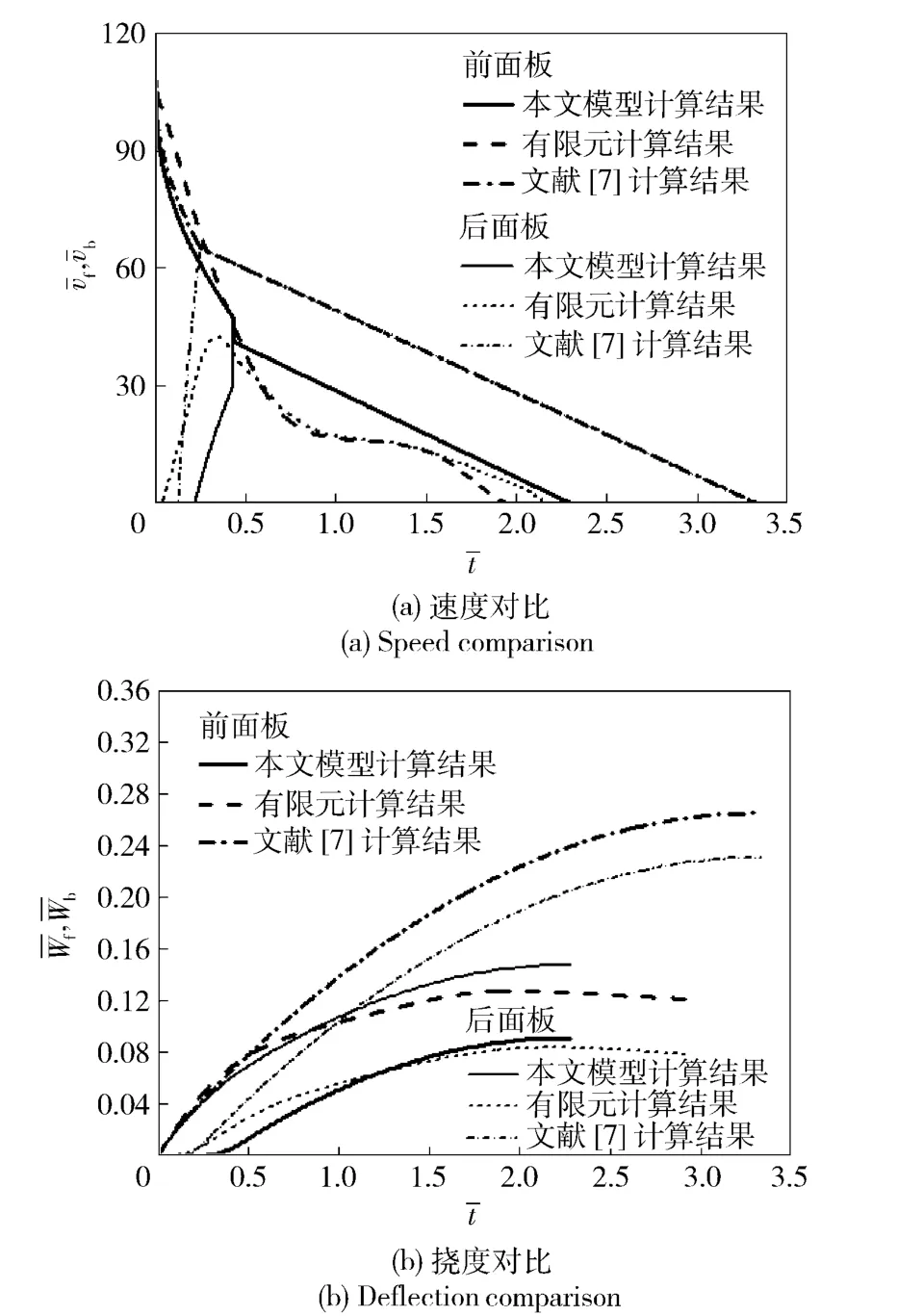
图6 计算模型与有限元及文献［7］模型关于上下面板中点速度和挠度的对比Fig.6 Comparison of analytical predictions of models in the present paper and Ref.［7］with respect to the data given by FE simulations for normalized mid-span velocity and deflection of front and back face-sheets

3 结论

本文基于小变形理论，并考虑三明治梁芯材在变形过程中的作用，提出了改进的三明治梁刚塑性模型，并对低冲量质量块作用下固支三明治梁的动力响应进行了讨论。与实验以及已有模型对比计算表明，在三明治梁芯材发生整体弯曲变形时，相较于文献［7］三明治梁模型，由于改进的模型在三明治梁整体变形前考虑了芯材的弯曲变形，可以更好地预测三明治梁的动力响应过程。同时，计算结果表明，当芯材发生剪切和破坏时，本文的模型不能很好地预测实验结果，这是因为本模型基于小变形假设。由于文章篇幅的限制，基于大变形的三明治梁模型这里不再讨论。

References)

［1］Fleck N A，Deshpande V S. The resistance of clamped sandwich beams to shock loading［J］. Journal of Applied Mechanics，2004，71(3):386 -401.

［2］Xue Z，Hutchinson J W. A comparative study of impulse-resistant metal sandwich plates［J］. International Journal of Impact Engineering，2004，30(10):1283 -1305.

［3］Rabczuk T，Kim J Y，Samaniego E，et al. Homogenization of sandwich structures［J］. International Journal for Numerical Methods in Engineering，2004，61(7):1009 -1027.

［4］Liang Y，Spuskanyuk A V，Flores S E，et al. The response of metallic sandwich panels of water blast［J］. Journal of Applied Mechanics，2007，74(1):81 -99.

［5］Deshpande V S，Fleck N A. One-dimensional response of sandwich plates to underwater shock loading［J］. Journal of the Mechanics and Physics of Solids，2005，53(11):2347 -2383.

［6］Taylor G I. The pressure and impulse of submarine explosion waves on plates［M］. The Scientific Papers of G I Taylor，vol Ⅲ.UK:Cambridge University Press，1963.

［7］Tilbrook M，Deshpande V S，Fleck N A. The impulsive response of sandwich beams:analytical and numerical investigation of regimes of behavior［J］. Journal of the Mechanics and Physics of Solids，2006，54(11):2242 -2280.

［8］Qin Q H，Wang T J，Zhao S Z. Large deflections of metallic sandwich and monolithic beams under locally impulsive loading［J］.International Journal of Mechanical Sciences，2009，51(11/12):752 -773.

［9］Qin Q H，Wang T J. Low-velocity heavy-mass impact response of slender metal foam core sandwich beam［J］. Composite Structures，2011，93(6):1526 -1537.

［10］Wang Z H，Lin J，Ning J G，Zhao L M. The structural response of clamped sandwich beams subject to impact loading［J］. Composite Structures，2011，93(4):1300 -1308.

［11］Jones N. Structural Impact［M］. Cambridge:Cambridge University Press，1989.