采用黄金分割法的自适应调制无线网络跨层设计

赵军辉， 田静秀， 李秀萍

1.北京交通大学电子信息工程学院，北京100044

2.东南大学移动通信国家重点实验室，南京210096

3.北京邮电大学电子工程学院，北京100876

为有效利用网络资源，提高网络吞吐量，在传统无线网络跨层设计方案中的物理层采用自适应调制编码(adaptive modulation and coding,AMC)[1].自适应调制是在不同的信道状态下选择不同的传输模式，以提高网络吞吐量.在传输模式的选取中，最重要的参数值就是目标误包率的取值，因为在不同的目标误包率下得到的网络性能差异很大.因此，选择一个恰当的目标误包率，能有效降低网络丢包率.

文献[2]考虑了当系统有足够的数据等待传输时，在数据链路层有限长缓冲区和自适应调制技术的联合作用下，系统的丢包率和吞吐量性能与系统目标误码率的关系，并在多用户场景下对此进行了分析.文献[3]分析了多跳网络的性能，通过对3个节点的简单多跳网络进行建模分析，考察了两跳网络中中继节点的位置对网络性能的影响，但没有有效利用跨层设计联合物理层、数据链路层以及其他层的参数对网络性能进行优化.文献[4]联合考虑了物理层的自适应调制技术、数据链路层的有限长缓冲区、传输层的TCP协议，分析了有效联合自适应调制和TCP协议的端到端系统性能，提出了一种优化物理层误码率的简单跨层设计.文献[5]提出了一种新型的基于自适应调制技术的跨层设计，将物理层的自适应调制技术与数据链路层的有限长缓冲区中的队列长度相结合，并引入新的设计参数，得到了一种基于自适应调制技术的速率选择方法，有效降低了网络的丢包率性能.文献[6-7]分别提出了一种能够改进自适应调制技术性能的方法，但都没有考虑到自适应调制技术的重要参数目标误码率对网络性能的影响.文献[8]联合考虑了自适应调制技术、有限长数据缓冲区队列长度以及多跳中继对网络的影响，通过建模分析得到了不同包到达率下网络的吞吐量以及丢包率性能的变化.文献[9]针对多跳Ad Hoc网络提出了一种基于分组碰撞和信道误码的自适应调制机制，该机制能支持多速率传输，有效提升了吞吐量性能和抗信道衰减性能.文献[10]针对异构网络环境下最佳中继、分集和服务分配等目标提出了一种跨网络跨层设计方法，经仿真证明该方法能显著提升网络性能.文献[11]基于压缩感知方法研究了无线传感网中的跨层拥塞控制算法，通过压缩传输信号并采用信道分配算法提高了无线传感网的拥塞控制能力.文献[12]则研究了跨层设计在低功耗无线传感网路由协议中的应用，基于模糊理论综合分析了一定范围内所有节点的电池剩余电量、链路性能以及传输功率等指标，从而得到最优路径选择.文献[13]考虑了多用户之间的公平性以及不同的服务类型对网络性能的影响.本文主要是在文献[2]的基础上进行改进，通过分析丢包率随误包率的变化趋势，利用黄金分割法对丢包率的函数进行优化，得到一定目标误包率范围内的最佳目标误包率，使得丢包率最小，即网络吞吐量最大.

1 系统建模

如图1所示，本文考虑的无线链路包括一根单发射天线和一根单接收天线[14].假设其物理层采用自适应调制技术，数据链路层采用有限长缓冲区，如图2所示.假设物理层可采用的调制模式有5种，如表1所示.

表1中，参数an、gn、γpn分别为近似即时误包率表达式中的参数，Rn代表调制模式为n时单位带宽下的传输速率.近似的即时误包率表达式为[2]

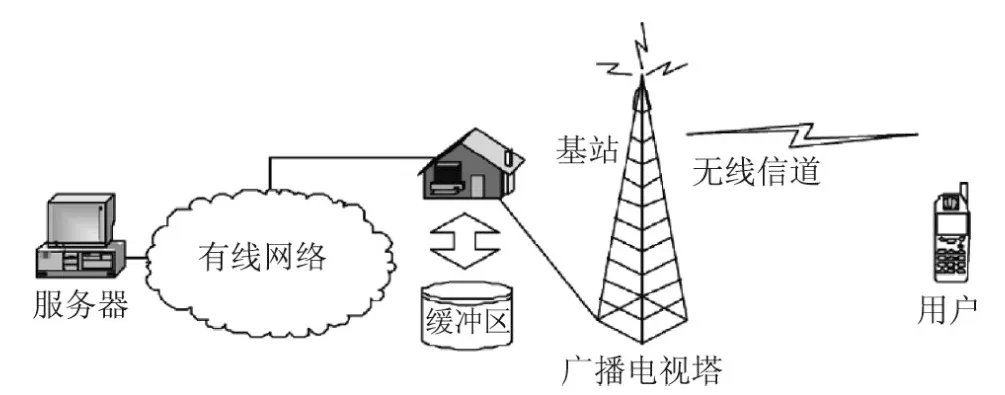
图1 端到端有线-无线连接Figur e 1 End-to-end wire-wireless connection

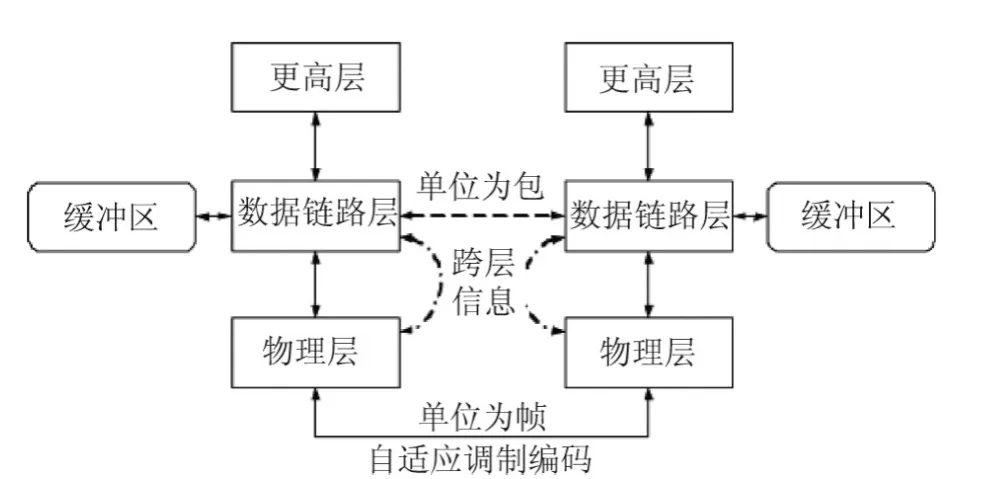
图2 联合AMC和队列分布的跨层结构Figure 2 Cross-layer structure of joint AMC and queue distribution

表1 自适应调制查找表Table 1 Adaptive modulation lookup table

一般假设物理层的目标误包率P0为一定值，根据假定的目标误包率要求可知：当可采用的调制模式有N种时，存在一个包含N+2个元素的调制方式阈值向量γ=[γ0,γ1,···,γN+1]T，将整个接收信噪比区域[0，+∞]划分为N+1个互不重叠的区域，其中γ0=0，γN+1=∞.采用文献[15]的算法确定调制门限，即选择γn使每种调制方式下的平均误包率均等于目标误包率P0，PERn=P0，其中

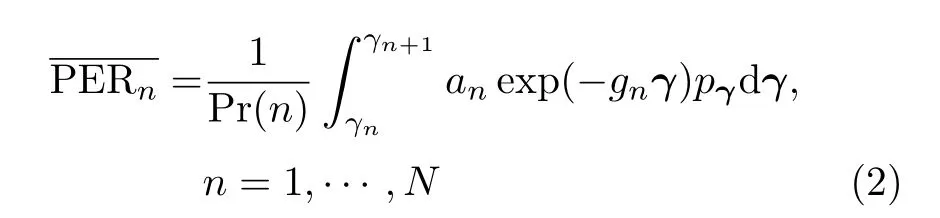
2 丢包率与目标误包率之间的关系

数据链路层采用有限长缓冲区，于是当缓冲区队列已满时，新到达的数据包就会溢出.假设包溢出率为Pd，数据包只有在信道中正确传输，且没有溢出时才算成功传输，于是可将丢包率表示为ξ=1-(1-Pd)(1-P0)，网络吞吐量表示为η=λTf(1-ξ)=λTf(1-Pd)(1-P0)，其中λTf为包达到率[1].由此可以看出，要评估网络的吞吐量和丢包率性能，最主要的问题是计算溢出包率Pd.

网络的溢出包率推导如下：

首先，分析节点处的输入流情况.假设节点的输入流分布服从参数为λTf的Poisson分布，其分布为

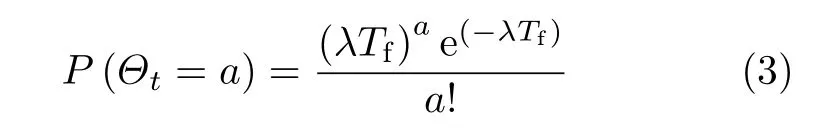
其次，分析其队列服务状态.假设信道的带宽为b，则每帧可传输的数据包数为cn=bRn.

最后，分析其队列和服务状态稳态分布.假设联合队列长度和服务速率的状态转移矩阵为PE=，其中矩阵元素的定义为

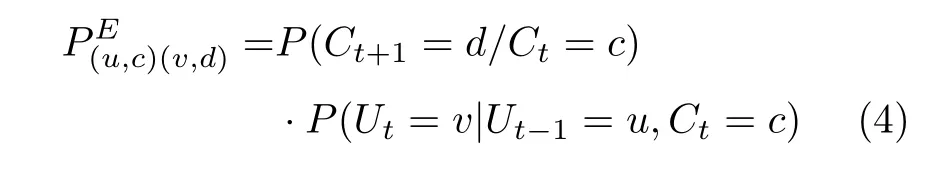
式中，速率转移概率P(Ct+1=d/Ct=c)用FSMC模型计算，P(Ut=v/Ut-1=u,Ct=c)可以进一步分解为

经过上述分析，可以得到由于缓冲区满而溢出的数据包的数目均值为

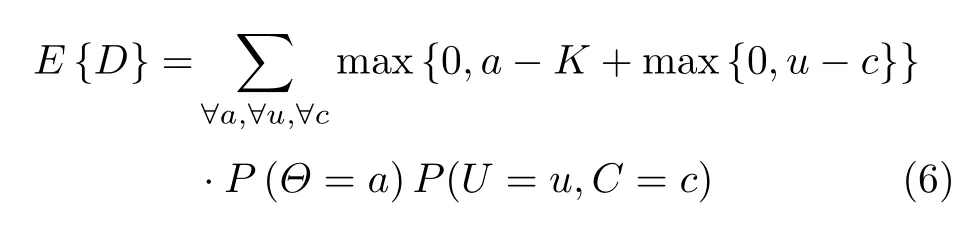
式中，K为缓冲区最大队列长度.进一步得到数据包溢出率为

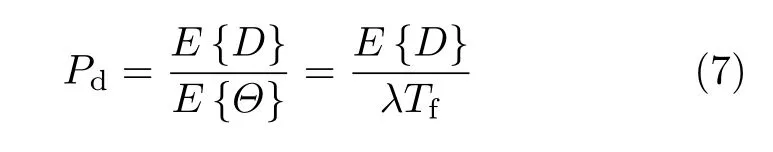
3 黄金分割法

由上述推导可以看出：当可采用的调制编码模式、信道带宽、传输信道信噪比、缓冲区长度等参量已知时，只要确定目标误包率P0的值，就可以根据式(2)推导出实时的信道传输速率c,进而计算出溢包率Pd的值，即Pd可看作目标误包率P0的函数pd=Pd(P0)，因而丢包率ξ=1-(1-Pd)(1-P0)可以看作目标误包率的函数，即ξ=ξ(P0).

假设在FSMC信道模型中，数据包都由1 080 bit组成，数据帧长Tf=2 ms，归一化多普勒频移fdTf=0.02，参数m=1，即仿真中采用瑞利信道模型．此外，信道带宽为2，节点处的缓冲区大小为50包，并且数据到达率为2包/帧.

通过MATLAB仿真得到网络的丢包率性能，如图3所示.分析不同目标误包率下丢包率的性能可以看出，无论信道的信噪比(signal noise ratio,SNR)多大，图3中丢包率随目标误包率的变化基本为二次曲线.因此，可以采用黄金分割法不断缩小取值区间，最终求得最佳目标误包率，可使丢包率最小.

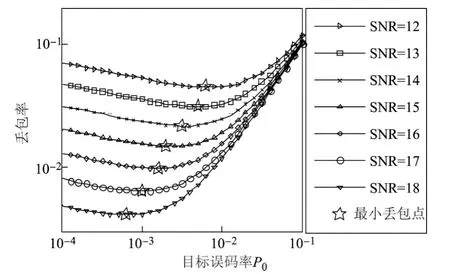
图3 丢包率与目标误包率的关系Figure 3 Comparison of packet loss rate and target packet error rate

黄金分割法也叫0.618法[17]，它是基于区间收缩的极小点搜索算法，通过不断缩小搜索区间，最终使搜索区间的端点逼近到最小点.

0.618 法是指在搜索区间[a，b]上选取两个对称点λ和µ，且λ＜µ，通过比较这两点处的函数值φ(λ)和φ(µ)的大小来决定删除左半区间[a,λ]，还是删除右半区间[µ,b].删除后的新区间长度是原来区间长度的0.618倍.新区间包含原区间中两个对称点中的一个，只要再选一个对称点，并利用这两个新对称点处的函数值继续比较即可.重复这个过程，最后确定极小点α∗.

本文同样假定搜索区间的两个端点，即目标误包率的取值范围分别为Pmin=0.0001到Pmax=0.1，黄金分割法首先根据黄金比例生成两个内点p1和p2，其计算公式分别为

然后根据ξ(p1)和ξ(p2)的大小关系重新选择搜索区间.若ξ(p1)＜ξ(p2)，则搜索区间变为[p1,Pmax]；若ξ(p1)＞ξ(p2)，则搜索区间变为[Pmin,p2].

具体的算法步骤如下：

步骤1 选定区间[0.000 1,0.1]，精度ε＞0，计算试探点

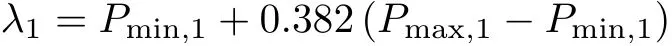
µ1=Pmin,1+0.618(Pmax,1-Pmin,1)，并令k=1；

步骤2 若Pmax,k-Pmin,k＜ε，则停止计算；否 则，当ξ(λk)＞ ξ(µk)时，转 步 骤3；当ξ(λk)≤ξ(µk)时，转步骤4.

步骤3 置

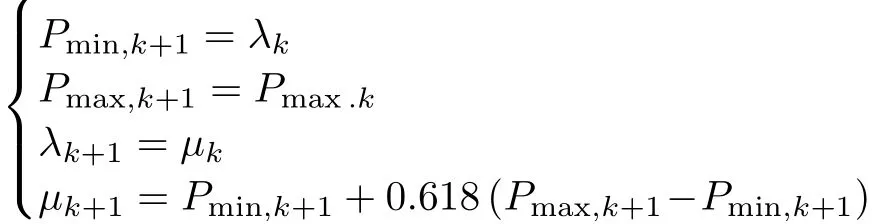
转步骤5.

步骤4 置

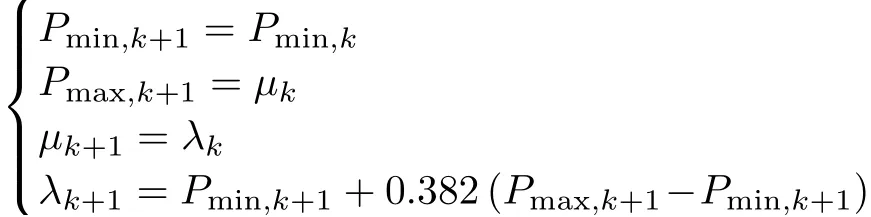
转步骤5.

步骤5 令k=k+1，转第2步.

由上述算法可知，最后当Pmax,k-Pmin,k＜ε时，循环结束，则最佳目标误包率可以表示为(Pmax,k+Pmin,k)/2，求得最小丢包率为ξ((Pmax,k+Pmin,k)/2).

利用黄金分割法对网络的目标误包率进行优化，找到不同信噪比下的最小丢包率，其仿真结果如图4所示.从图4中可以看出，通过黄金分割法找到的目标误包率对应的丢包率值基本与不同信噪比下的最小丢包率一致，即通过黄金分割法找到了最佳的目标误包率，使网络丢包率最小.

4 仿真结果分析

为了更清楚地观察优化后的性能变化，将通过黄金分割法优化得到的丢包率与目标误包率分别为0.1、0.01、0.001、0.0001时的丢包率性能和吞吐量性能分别进行比较，其结果如图5所示.从图5中可以看出，其丢包率性能和吞吐量性能均优于任何一种目标误包率一定的情况.

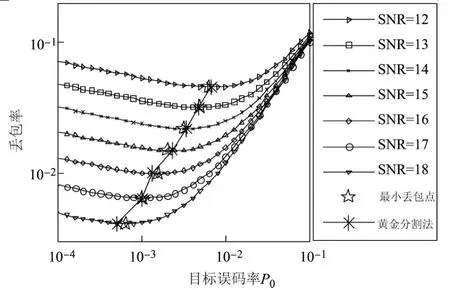
图4 黄金分割法得到的网络丢包率Figure 4 Packet loss rate of golden selection method

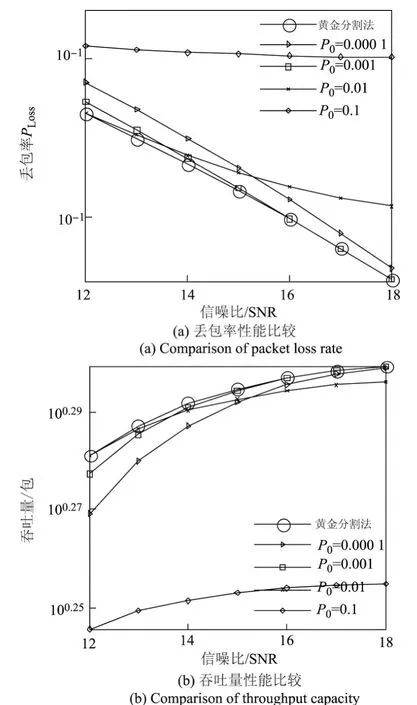
图5 不同目标误包率选择方式下的性能比较Figure 5 Comparison of different target packet error rate selection methods

5 结语

在无线网络跨层设计中，一般指定物理层的目标误包率为一个确定值，便于研究者直观地观察网络的物理层性能.然而，在不同目标误包率的情况下，网络的丢包率性能是不相同的，因此确定的目标误包率在一定程度上限制了网络的丢包率和吞吐量性能.本文通过理论分析，考察了丢包率与目标误包率之间的关系，并利用黄金分割法求出在一定条件下能达到的最小丢包率所对应的目标误包率值.仿真结果表明，黄金分割法能有效地找到最佳目标误包率，使网络的丢包率最低，吞吐量最大.本文仅仅分析了单用户情况，虽然提升了网络的总体吞吐量性能，但是没有考虑到多用户之间的公平性以及不同的服务类型对网络性能的影响，这也是下一步的研究重点.

[1]程鹏，张朝阳，黄慧，仇佩亮.结合自适应调制和ARQ的跨层最优联合设计[J].西安电子科技大学学报：自然科学版，2008,35(1):171-174.

CHENG Peng,ZHANG Chaoyang,HUANG Hui,QIU Peiliang.Optimal joint design of adaptive coded modulation and ARQ[J].Xidian University:Natural Science Edition,2008,35(1):171-174.(in Chinese)

[2]LIUQ,ZHOUS,GIANNAKISG B.Queuing with adaptive modulation and coding over wireless links:crosslayer analysis and design[J].IEEE Transactions on Wireless Communications,2005,4(3):1142-1153.

[3]ZHENG K,WANG Y,LEI L,WANG W.Cross-layer queuing analysis on multihop relaying networks with adaptive modulation and coding[J].IET Communications,2010,4(3):295-302.

[4]LIU Q W,ZHOU S L,GIANNAKISG B.TCP performance in wireless access with adaptive modulation and coding[C]//IEEE International Conference on Communications,2004:3989-3993.

[5]PAKDEHIA,ASHTIANIF.A new cross layer design of adaptive modulation and coding in f inite buffer wireless links[J].Future Generation Communication and Networking,6-8 Dec,2007:499-504.

[6]BAI X,SHAMI A.A new perspective of cross-layer optimization for wireless communication over fading channel[J].Computer Communications and Networks,13-16 Aug,2007:1-6.

[7]PAKDEHIA,ASHTIANIF.Cross-layer optimization of adaptive modulation and coding preserving packet average delay time[C]//IEEE GLOBECOM,New Orleans,LO,2008:1-5.

[8]CHENG Peng,YU Guanding,ZHANG Zhaoyang,JIA Huiling.Cross-layer performance analysis of two-hop wireless links with adaptive modulation[C]//IEEE 17th International Symposium on Personal,Indoor and Mobile Radio Communications,Helsinki,2006:1-5.

[9]成德峰，马刈非.Ad Hoc网络中基于信道状态的速率自适应机制[J].应用科学学报，2008,26(1):18-21.

CHENG Defeng,MA Liufei.A rate adaptation mechanism based on channel state in Ad Hoc network[J].Journal of Applied Sciences,2008,26(1):18-21.(in Chinese)

[10]JU Honghao,LIANG Ben,LI Jiangdong,LONG Yan,YANG Xiaoniu.Adaptive cross-network cross-layer design in heterogeneous wireless networks[J].IEEE Transactions on Wireless Communications,2014,13(9):1-15.

[11]HONG W,NADER M.Finite-state Markov channela useful model for radio communication channels[J].IEEE Transactions on Vehicle Technology,1995,44(1):163-171.

[12]LI C T,WANG J K,HAN Y H.An efficient compressed sensing-based cross-layer congestion control scheme for wireless sensor networks[C]//The 26th Chinese Control and Decision Conference(2014 CCDC),Changsha,China,2014:637-641.

[13]JARADAT T,BENHADDOUD,BALAKRISHNANM,ALFUQAHA A.Energy efficient cross-layer routing protocol in wireless sensor networks based on fuzzy logic[C]//9th International Wireless Communications and Mobile Computing Conference,Sardinia,2013:177-182.

[14]LIU Q,ZHOU S,GEORGIOS B.Cross-layer combining of queuing with adaptive modulation and coding over wireless links[J].IEEE Military Communications Conference,Oct 2003:13-16.

[15]MITRA A.A PHY-MAC cross layer design for low PER with adaptive modulation and coding[C]//International Workshop on Cognitive Radio(IWCR),Bangalore,2010:1-5.