带有通信噪声的随机时延复杂动态网络的H∞控制

韦庆阳， 樊春霞， 顾 瑜

南京邮电大学自动化学院，南京210003

近年来，复杂动态网络成为各个领域的研究热点[1-6]，其控制与同步问题也得到了很多关注.由于网络本身的很多元素，如网络拓扑结构变化、时间延迟、通信噪声等，复杂网络的同步控制面临诸多具体问题[7-8].

复杂动态网络节点之间进行信息传输，不可避免地受到信道噪声干扰，且随机发生传输时延.文献[9]考虑存在依赖于系统状态且满足伯努利分布的白噪声干扰情况下，时滞离散复杂动态网络的同步控制问题.文献[10]针对传感器存在随机时延和随机饱和的情况，研究了复杂网络的状态估计问题.文献[11]针对非线性节点和有随机干扰的延迟复杂网络，采用混合自适应方法和脉冲控制方法实现了随机同步.文献[12]实现了针对带有随机耦合强度变化和不确定性节点延迟的马尔科夫耦合神经网络的同步控制.文献[13]研究了随机切换耦合结构的复杂网络的同步问题.文献[14]提出了一种节点状态信息通信时随机发生延迟的复杂动态网络模型，并给出了同步控制器存在准则，由此可见，随机因素作为复杂网络研究中不可忽略的因素，逐步成为该领域的热点问题.

文献[14]不但提出了随机时延复杂动态网络的模型，而且给出了该网络模型同步控制器的存在准则，但没有考虑节点间在传输状态信息时存在的信道噪声.文献[5]利用牵制控制的方法，以最少数量的控制器获得了节点受到噪声干扰的线性耦合随机神经网络的同步.该网络中的噪声由布朗运动描述，且依赖于系统状态.每个节点噪声的强度与该节点状态量呈现出某种函数关系.对于这种噪声，文献[5]采用伊藤积分的方法来处理.

本文研究具有随机时延和信道噪声的复杂动态网络，所考虑的信道噪声不依赖于系统状态，采用H∞控制方法来抑制噪声对网络稳定性的影响.利用Lyapunov稳定性理论、随机分析方法与H∞控制方法，实现了一个带有信道噪声的随机时延复杂动态网络的控制.将复杂动态网络的节点信息在传输过程中的时延描述成Markov链形式，建立了随机时延耦合的复杂动态网络H∞控制器设计准则.最后，以Lorenz混沌系统作为节点动力学，构造了复杂动态网络并进行数值仿真.仿真结果表明，本文所提出的控制器能够将具有随机时延的复杂动态网络渐近稳定在平衡点，且满足一定的H∞性能指标.

1 建立网络模型和设计控制器

考虑包含N个节点的随机时延耦合的复杂动态网络

式中，xi(t)=(xi1(t),xi2(t),···,xin(t))T∈Rn是节点i的状态向量；f:Rn→Rn为非线性平滑向量值函数，˙xi(t)=f(xi(t))为节点动态方程，A为任意两个节点之间的内部耦合矩阵，ui(t)为控制输入，τ(t)为网络耦合的延迟时间，C=(cij)N×N为复杂网络的耦合拓扑矩阵，wj(t)∈L2[t0,∞)是节点j的状态xj传输到节点i时受到的信道噪声干扰，B∈Rn×n为一个常数矩阵，决定了通信噪声wj(t)的强度，δ(t)∈[0,1]表示是否发生时延的随机变量.如果第i个节点与第j(i/=j)个节点有连接，则cij＞0；否则，cij=0(i/=j)，且cii=0(i=1,2,···,N).若复杂网络中没有孤立的簇，则C对称不可约[17].δ(t)=1表示一个节点的邻居节点状态向量xj(t)在传输到该节点的过程中没有发生时间延迟，δ(t)=0表示一个节点的邻居节点状态向量xj(t)传输到该节点的过程中会发生时间延迟.δ(t)是一个Markov链，且满足如下的指数分布变换[18-19]：

注1 在复杂网络(1)中，节点i的信息不通过网络传递到该节点，因此不用考虑信息传输时延以及信道噪声；在文献[14]提出的随机时延耦合复杂动态网络模型中，节点i的信息通过网络传递到该节点，因而节点自身信息耦合时也发生了时延.从工程实现角度来讲，节点i的信息可以直接传递该节点，而没有必要通过网络传递，故不增加网络的通信负载.从这个意义上来说，复杂网络(1)比文献[14]中提出的网络模型更符合工程实际.

注2 复杂网络(1)考虑的是信息在节点之间的传输时延以及信道噪声对网络稳定性的影响，文献[5,10-12]中的节点动力学是时延系统，而对于信息在网络上的传输过程没有给予更多的关注.

假设1 复杂网络(1)中的时延τ(t)满足

式中，τ1、τ2、h均为正数，h为延迟时间变化率的界.假设2 非线性函数f(·)满足Lipschitz条件

式中，x和y表示任意时变n维向量，Li是一个正数，且i=1,2,···,n，记作L=diag{L1,L2,···,Ln}.

采用反馈控制的原理设计控制器

式中，控制器增益ki是待确定的.将式(6)代入式(1)，则得到被控网络为

由假设2可得

定义1 若wi(t)=0，且满足E(˙V(t))≤0，则被控复杂动态网络(6)在均方意义下渐进稳定.

本文旨在给出控制器(5)的设计准则，使得复杂动态网络(6)满足以下2个条件：

1)当wi(t)=0时，复杂动态网络(6)是均方意义下的渐近稳定.

2)当wi(t)/=0(i=1,2,···,N)时，在零初始条件下，被控动态网络(6)的状态满足

式中，r为给定的标量，且r＞0.本文需要引入引理1和2.

引理1[20]对于任意两个向量x,y∈Rn和标量ε＞0，不等式2xTy≤εxTx+ε-1yTy成立.

引理2[21]矩阵Schur补引理.线性矩阵不等式

式中，Q(x)=QT(x)、R(x)=RT(x)和S(x)映射于x，等价于

2 复杂动态网络的H∞控制

下面研究复杂动态网络(6)的H∞控制问题.

定理1 如果存在标量ε＞0，对称正定矩阵P和Q，满足矩阵不等式

证明 取Lyapunov-Krasovskii泛函为

式中，P和Q均为对称正定矩阵.对V(t)求导，可得

根据引理1和假设2可得

令Z(t)=(x1(t)T,···,xN(t)T)T，可得式(16)～(24)

因此可得

式中，U=I3N+(˙τ(t)-1)(IN⊗Q)对式(25)的两边求期望值，因为

所以

式中，U1=I3N+(H-1)(IN⊗Q)

利用引理2对式(27)进行变换，可得式(11)和(12).当且仅当M1＜0，式(12)成立.

根据Lyapunov稳定性理论可知，当wi(t)=0时，在控制器(5)作用下，被控网络(6)是均方意义下的渐近稳定.

定理2 给定H∞性能指标r＞0.如果存在标量ε＞0和对称正定矩阵P、Q，满足矩阵不等式

式中，M2=(C⊗(PAB))

则带有通信噪声的随机时延复杂动态网络(6)是均方渐近稳定的，且对于所有非零点，wi(t)(i=1,2,···,N)能满足H∞性能指标(8).

那么，考虑式(16)～(24)和式(29)可得

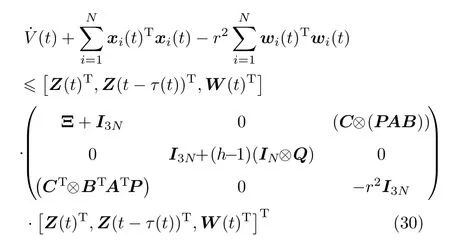
考虑时间t服从时间[t0,∞)，将式(30)两边积分可得

在零初始条件下，可得V(t0)=0和V(∞)≤0，

注3可以用MATLAB软件的YALMIP工具箱求解控制器设计的准则线性矩阵不等式(11)和(12).

3 数值仿真

在仿真中，建立一个包含10个节点的随机时延耦合复杂网络，其中每个节点采用Lorenz系统.Lorenz系统的表达式为

式中，a、b、c均为参数.当a=10，b=8/3，c=28时，该系统出现混沌特性.在被控网络式(6)中，选定性能指标r=0.5，δ(t)是满足式(2)的马尔科夫链

外部耦合矩阵为

在仿真中，耦合延迟时间设定为函数τ(t)=0.3+0.1sin t，且延迟时间函数导数的界h=0.1.本文选择高斯噪声作为通信噪声，则网络节点的初始状态为

当控制器的增益ki=50,i=1,···,10,=0.5时，求解线性矩阵不等式=0.5可得

仿真结果如图1所示.由图1可以看出，复杂网络(1)在控制器(5)的作用下所有节点的状态渐近稳定，满足r=0.5的性能指标.

图1 当=0.5时，受控复杂动态网络节点的状态xi1、x i2、x i3Figure 1 State x i1、x i2、x i3 of controlled complex networks whenδ=0.5

4 结语

本文研究了信道噪声环境下随机时延复杂动态网络的控制问题.考虑到节点之间信息传输时不可避免地受到信道噪声的干扰以及传输时延的随机发生，设计了状态反馈控制器.利用Lyapunov稳定性理论、随机分析方法和H∞控制方法，得到了信道噪声环境下的随机时延耦合复杂动态网络控制器设计准则.最后，以Lorenz混沌系统作为节点，构建了复杂动态网络进行数值仿真.仿真结果表明，本文所设计的状态反馈控制器能够使带有信道噪声的随机时延复杂动态网络渐近稳定，并且满足给定的H∞性能指标.

[1]HIROSE A,YOSHIDA S.Generalization characteristics of complex-valued feed forward neural networks in relation to signal coherence[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(4):541-551.

[2]蒋国平，樊春霞，宋玉荣，邵斐.复杂动态网络同步控制及其在信息物理系统中的应用[J].南京邮电大学学报：自然科学版，2010,30(4):41-51.

JIANG Guoping,FAN Chunxia,SONG Yurong,SHAO Fei.Synchronization and control of complex dynamical networks with applications in cyber-physical systems[J].Journal of Nanjing University of Posts and Telecommunications:Natural Science,2010,30(4):41-51.(in Chinese)

[3]何汉林，涂键君，熊萍.基于离普希茨常数估计的混沌鲁里叶系统同步[J].系统工程与电子技术，2011,33(3):600-602.

HEHanlin,TUJianjun,XIONGPing.Chaos synchronization between lurie systems based on estimation of Lipschitz constant[J].Systems Engineering and Electronics,2011,33(3):600-602.(in Chinese)

[4]FANChunxia,JIANGGuoping,JIANGFenghua.Synchronization between two complex dynamical networks using scalar under pinging control[J].IEEE Transactions on Circuits and Systems,2010,57(11):2991-2998.

[5]LU J Q,DANIEL W C H,WANG Z D.Pinning stabilization of linearly coupled stochastic neural networks via minimum number of controllers[J].IEEE Transactions on Neural Networks,2009,20(10):1617-1629.

[6]LIU D,MICHEL A N.Cellular neural networks for associative memories[J].IEEE Transaction on Circuits and Systems II,Analog Digit Signal Processing,1993,40(2):119-121.

[7]LI Z,JIAO L,LEE J J.Robust adaptive global synchronization of complex dynamical networks by adjusting time-varying coupling strength[J].Physica A,2008,387(5/6):1369-1380.

[8]YANG Xinsong,CAO Jinde,LU Jianquan.Synchronization of delayed complex dynamical networkswith impulsive and stochastic effects[J].Nonlinear Analysis:Real World Application,2011,12(4):2252-2266.

[9]WANG Zidong,WANG Yao,LIU Yurong.Global synchronization for discrete-time stochastic complex networks with randomly occurred nonlinearities and mixed time delays[J].IEEE Transactions on Neural Networks,2010,21(1):11-25.

[10]DINGDerui,WANGZidong,SHENBo,SHUHuisheng.H∞state estimation for discrete-time complex networks with randomly occurring sensor saturations and randomly varying sensor delays[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(5):725-736.

[11]YANGXinsong,CAOJinde,LUJianquan.Stochastic synchronization of complex networks with nonidentical nodes via hybird adaptive and impulsive control[J].IEEE Transactions on Circuits and Systems,2012,59(2):371-384.

[12]YANG Xinsong,CAO Jinde,LU Jianquan.Synchronization of Markovian coupled neural networks with nonidentical node-delays and random coupling strengths[J].IEEE Transactions on Neural Networks and learning Systems,2012,23(1):60-71.

[13]LIU Bo,LU Wenlian,CHEN Tianping.Synchronization in complex networks with stochastically switching coupling structures[J].IEEE Transactions on Automatic Control,2010,57(3):754-760.

[14]CHEN Maoyin.Synchronization in complex dynamical networks with random sensor delay[J].IEEE Transaction on Circuits and Systems II,2010,57(1):46-50.

[15]BALASUBRAMANIAM P, VEMBARASAN V,RAKKIYAPPAN R.Delay dependent robust exponential state estimation of Markovian jumping fuzzy hopf ield neural networks with mixed random time-varying delays[J].Communications in Nonlinear Science and Numerical Simulation,2011,16(4):2109-2129.

[16]LIU Yurong,WANG Zidong,LIANG Jinling,LIU Xiaohui.Stability and synchronization of discretetime markovian jumping neural networks with mixed mode dependent time delays[J].IEEE Transactions on Neural Networks,2009,20(7):1102-1116.

[17]PECORA L M,CARROLL T L.Master stability functions for synchronized coupled systems[J].Physical Review Letters,1988,80(10):2109-2112.

[18]LIN Chong,WANG Zidong,YANG Fuwen.Observerbased networked control for continuous-time systems with random sensor delays[J].Automatica,2009,45(2):578-584.

[19]YUE D,TIAN E G,WANG Z D,LAM J.Stabilization of systems with probabilistic interval input delay and its applications to networked control systems[J].IEEE Transactions on Systems,Man and Cybernetics,Part A:Systems and Humans,2009,39(4):939-945.

[20]WANG Jianan,LIU Heping,SHI Xin.Adaptive synchronization between two complex networks with nonidentical topological structures and time-varying delay coupling[J].Journal in Beijing University of Technology,2010,32(12):132-138.

[21]BOYD S,GHAOUI L,FERON E,BALAKRISHNAN V.Linear matrix inequalities in system and control theory[M].Society for Industrial and Applied Mathematics,1994.