多重JPEG压缩图像的压缩痕迹检测
韩洪立, 李叶舟, 牛少彰, 孙晓婷
1.北京邮电大学理学院,北京100876
2.北京邮电大学智能通信软件与多媒体北京市重点实验室,北京100876
JPEG图像因占用空间资源少、便于传输和存储等优点在互联网上得到了广泛应用.资料显示,网站上80%的图像均采用JPEG压缩标准.现在流行的图像处理软件种类繁多,操作简单,这在一定程度上使得图片被篡改的现象十分常见,同时也对互联网络的安全和秩序造成了影响.因此,针对JPEG图像篡改检测的研究意义重大.目前针对JPEG图像篡改的检测手段多种多样,最近也有了许多新的研究方向,如基于EXIF信息的篡改取证[1-2],基于检测数字照片中的光照方向与物体投影的不一致性[3-5],基于相机参数等特性的研究[6-7]等.另外,如基于数字照片中场景不一致特性的研究[8]也成为图像篡改取证的一个新方向.同时,根据图像的统计特性等(如重采样特性、复制-粘贴特性、JPEG压缩不一致等)进行篡改检测[9-11]始终是一个重要的研究方向.特别是针对JPEG压缩不一致性进行篡改检测,由于篡改者在对JPEG图像修改完成后通常将图像以JPEG格式重新保存,这一过程难免会引入图像经历JPEG重压缩的某些数据特征.本文也将针对JPEG图像受到篡改时又经过多重JPEG压缩这一情况进行研究.
事实上,篡改者在整个篡改过程中经常对图像进行多次修改和保存,这就难免会引入对JPEG图像不确定次数的重压缩.同时,当被篡改JPEG图像传到网站服务器时,很多网站服务器为了节约存储资源也常常对其进行压缩.经历了多重JPEG压缩的篡改图像,许多篡改痕迹已经不明显,这也使得许多针对图像数据特征进行篡改取证的方法受到限制.针对互联网上低质量因子JPEG图像发生篡改这一情形展开了研究及分析,通过研究JPEG图像在经历双重压缩以及多重压缩后的数据变化规律,发现图像在经历了先小后大质量因子的多重JPEG压缩时,可通过结合“去压缩”来依次找到图像经历的压缩痕迹,并对其图像数据进行逐步近似的恢复.若能将图像数据恢复至相对原始的状态,便可以通过现有的一些篡改检测方法对其进行检测,这在一定程度上减少了因图像经历多重JPEG压缩后无法有效地通过现有的一些图像篡改检测算法进行取证的限制.
1 针对多重JPEG压缩的去压缩检测算法
文献[12]提出了一种利用图像经过双重JPEG压缩会出现特殊的统计特性来进行双重JPEG压缩检测方法.相对于此前通过DCT系数分布特征来进行检测的方法(需要依赖于模型的训练,检测过程复杂),该方法相对简单并且检测效果较好,但图像经过了多重JPEG压缩后,这种相关性会受到较大的削弱.在大量实验中发现,在图像经历多重JPEG压缩的情况下,JPEG Ghost方法很多时候会出现完全无法进行压缩痕迹的检测或者出现大量的误检情况.去压缩检测算法结合JPEG Ghost检测方法的部分思想并利用“去压缩”可对图像进行较全面的压缩痕迹检测.
1.1 去压缩检测算法的理论基础
定义20个量化矩阵{Q1,Q2,···,Q20},其对应的质量因子依次为5%,10%,···,100%. 假设待检测图像I(JPEG格式)经历了多重JPEG压缩,且图像I由原始图像I0(BMP格式)依次经历了量化矩阵Qα1,Qα2,···,Qαn压缩后得到,其中α1<α2<···<αn.在这里引入一个“去压缩”的概念,其实质是在图像经历了先小后大质量因子压缩后,若能找到它前一次经历的压缩痕迹,便可以对其图像数据进行一次近似恢复.也就是说,若能找到图像I经历的最后两次的压缩痕迹Qαn-1和Qαn,并将待检测图像I用量化矩阵Qαn-1压缩,可使图像I近似恢复到原始图像I0依次经历量化矩阵Qα1,Qα2,···,Qαn-1压缩后的状态,即将图像I的数据近似恢复到尚未经量化矩阵Qαn压缩前的状态.将这一规律在文中表述为图像I去除了量化矩阵Qαn的压缩,于是可逐步使图像I近似恢复至原始图像I0刚经历量化矩阵Qα1压缩后的状态.“去压缩”方式对图像数据进行近似恢复时,只需将待检图像用图像前一次经历的量化矩阵进行压缩即可.
为对“去压缩”的合理性进行说明,不妨假设原始BMP图像Iorg(Iorg为对该图像灰度值进行DCT变换后得到的DCT系数矩阵).对原始图像Iorg分别进行下面操作.
1)将原始图像Iorg用量化矩阵Qαk进行压缩并保存,得到图像I1(JPEG格式).
2)将原始图像Iorg先后用量化矩阵Qαk和Qαk+1分别进行压缩并保存,得到图像I2(JPEG格式).
文中针对图像经历先小后大质量因子压缩这一情况进行了研究,在这里有αk<αk+1.将图像I2用量化矩阵Qαk进行第3次压缩并保存得到图像I3,对于图像I3任意一个8×8变换块(此文用8×8分块进行说明)的DCT量化系数矩阵(i,j)(i,j=1,2,···,8)处的值V(i,j)应满足


可将式(2)进一步化简可得

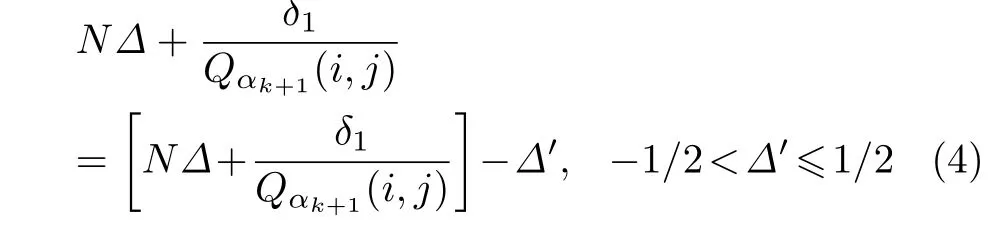
将式(4)移项可得

将式(5)代入式(3),有

整理式(6)可得
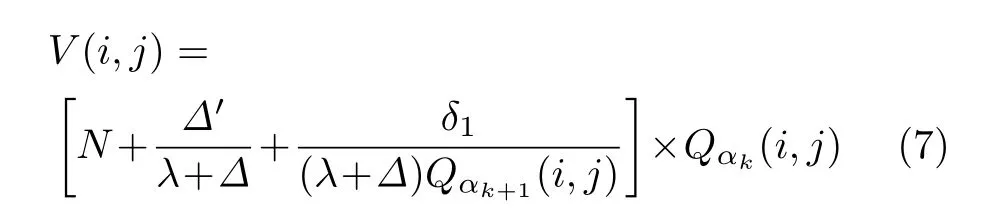
分析式(7)式且设式(8)成立,在本小节末将对式(8)的合理性进行说明.

此时考虑到αk<αk+1,故成立,则有
1)若Δ=0,由αk<αk+1可知λ≥2且为整数,则≤1/4,于是


由式(9)和(10)可知,在αk<αk+1的情况下,若式(8)成立,对式(7)则有V(i,j)=NQαk(i,j).
为对式(8)进行说明,先讨论参数δ1.当αk<αk+1时,有成立(式(9)和(10)中已说明过),若式(8)成立,应有

于是,可求θmin=1/2,=-1/2.则当|δ1|<θmin=||=1/2时必有式(8)成立.该成立条件可作为充分不必要条件,因为没有涵盖全部的情况.另外,需要说明Qαk(i,j)和Qαk+1(i,j)在很少的情况下会相等,一般前者与后者之差至少大于1.同时由于两者相等出现的位置一般处于DCT高频分量部分,大部分变换块的DCT高频分量为0.这里给出的是充分条件,两者相等时在多情况下有式(8)成立.
为了便于说明,从CASIA数据库中选取50组原始图像数据进行测试,将原始图像数据按上面操作过程分别压缩成图像I1和I2.
图1中的αk表示图像I2前一次经历的量化矩阵对应的编号,αk+1表示I2当前经历的量化矩阵对应的编号.对I2用量化矩阵Qαk进行“去压缩”后得到图像I3.统计I1与I3DCT系数相等部分(统计时除去I1与I3中均为0的DCT系数部分)所占的比例.对50张图片进行统计平均,统计结果见图1,图中虚线三角区域是I2经历先小后大质量因子压缩时的统计结果,对图中该区域进行分析可知I1与I3DCT系数基本相同,这也就从实验上证明了“去压缩”的合理性.对于图像经历先大后小质量因子压缩的情况不适用此方法.

图1 I3(I2“去压缩”后)与I1 DCT系数匹配程度说明图Figure 1 Matching degree of DCT coefficients between I3 and I1
1.2 去压缩检测算法的实现过程
当图像经历先小后大质量因子压缩时,去压缩检测算法的实现依赖于能否对待检测图像进行“去压缩”(或近似数据恢复),而“去压缩”实现的关键又在于能否依次找到图像经历的前一次压缩痕迹.近年来,关于如何检测图像的双重JPEG压缩痕迹许多学者、专家提出了新的检测算法,主要有文献[13-14]提出的通过DCT系数分布直方图进行双重JPEG压缩图像首次量化矩阵估计算法.该算法将双重JPEG压缩图像的DCT系数分布直方图中所呈现的分布规律量化为0,1序列,并利用文献[15]的结论对图像进行适当裁剪,近似估计图像未经压缩前的DCT系数;之后对估计得到的DCT系数进行双重JEPG压缩仿真实验,并与真实的DCT系数分布直方图比特序列相比较,找到最佳匹配值,以此估计整个DCT系数量化矩阵.文献[16]提出了一种双重JPEG压缩首次量化矩阵估计算法,从检测结果来看,在推断图像首次量化矩阵的高频区域量化步长时,该检测算法相较于文献[17]的算法有了一定的改善.
文献[13-15]中双重JPEG压缩检测算法的主要目标是设法估计出相对准确的首次量化矩阵,而本文实验模型及应用场景假定了JPEG图像在压缩时所采用的量化矩阵是常用的量化矩阵,即只要确定了首次量化矩阵中的直流分量的量化步长即可同时确定其他交流分量的量化步长,并没有将大量工作放在如何还原首次量化矩阵上,而侧重于找到图像前一次压缩痕迹即可.为此,本文针对该场景提出了新的多重JPEG压缩痕迹检测算法,该检测算法以文献[12]中JPEG Ghost检测算法为原型.
JPEG Ghost检测方法[12]在图像经历两次质量因子相差较大的双重JPEG压缩时检测效果较好,而在质量因子比较接近时无法检测甚至出现误检.若仅通过JEPG Ghost方法进行压缩痕迹检测,则在很大程度上限制了去压缩检测算法的适用范围.在大量实验的基础上,发现利用JPEG图像的DCT系数直流分量(即DC系数)在经历不同量化矩阵量化时,其量化误差会表现出类似于JPEG Ghost方法中的误差分布特点,并且在检测图像经邻近质量因子压缩时有明显的优势.
文献[18]中指出,若待测图像D经过两次JPEG压缩,对应质量因子依次为P1和P2.对图像D进行适当分块,记为B(1,1),···,B(m,n),待检测的图像D就是由所有的这些分块构成的集合,即D={B(1,1),···,B(m,n)}.
对D中的每个分块进行DCT差值特征提取.分块的DCT差值特征提取就是将图像D的一个分块B(x,y)按照质量因子p进行压缩(p=5%,10%,···,100%),计算压缩前后分块的DCT系数的差值D(x,y,p)
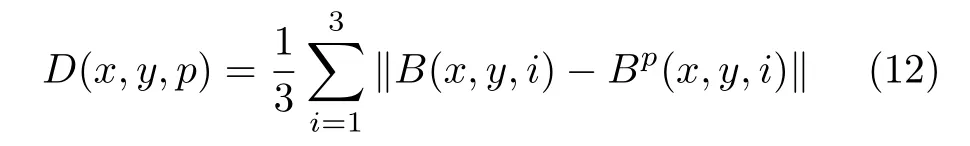
式中,B(x,y,i),i=1,2,3分别代表R、G、B三个颜色通道对应B(i,j)分块位置上的DCT系数矩阵,Bp(x,y,i)表示经过质量为p的JPEG压缩后的DCT系数矩阵,||.||表示计算二范数.
对于灰度图像,DCT系数的差值D(x,y,p)就简化为

计算得到分块B(x,y)在不同质量因子下的DCT系数差值,序列中的极小值点对应分块经历的压缩质量因子.文献[18]对JPEG Ghost方法检测双重JPEG压缩痕迹基本原理作了说明.
在针对图像经历邻近质量因子压缩时JPEG Ghost方法无法有效地进行检测这一问题,本文通过大量实验进行研究分析发现,通过计算DCT系数直流分量的量化误差能够取得相对较好的检测结果.对式(12)情况,DCT系数的差值计算表达式为
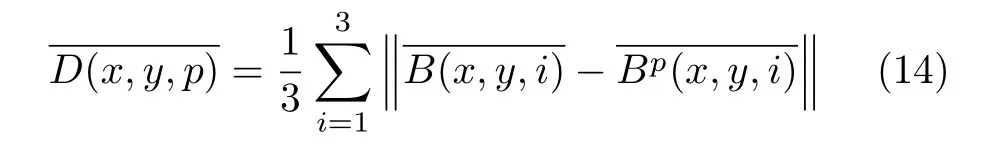
对于灰度图像可计算

B(x,y,i)、Bp(x,y,i)、B(x,y)、Bp(x,y)表示各自DCT系数的直流分量,表示DCT系数直流分量的差值.其他符号与式(12)和(13)一致.
文献[12]在提到JPEG Ghost时,并未对此给出严格的限定和说明.本文针对研究图像在经历先小后大质量因子压缩这一情形,为对大量图像数据进行检测实验需要设定一个JPEG Ghost判定标准.这里设定的JPGE Ghost判别标准为:用小于待检测图像(JPEG格式)当前质量因子的一组量化矩阵(文中的量化矩阵与质量因子一一对应)对其进行压缩,计算压缩前后DCT系数的误差值.在正常情况下,未经多重JPEG压缩的图像计算得到的误差值增减与质量因子大小存在对应的规律.一般来说质量因子越小对应误差值越大,反之亦然.如果在该检测误差序列中存在极小值点,可判定它对应图像前一次经历的压缩的质量因子.将极小值点(如存在不止一个,判定为其中最小的极值点)对应的质量因子判定为次JPEG Ghost点,简记次Ghost点,表示图像前一次经历的压缩痕迹.在此判断标准下,选取了CASIA(tampered image detection devaluation database)中的50张图片(BMP格式测试数据)进行压缩和检测实验.质量因子P1是对图像进行首次JPEG压缩的质量因子,P2是对图像进行第2次JPEG压缩的质量因子.为对DCT系数直流分量(即DC系数)量化误差检测法和JPEG Ghost检测法在检测图像经历邻近质量因子压缩时的检测效果差异进行说明,仅对P2-P1≤25%部分进行压缩和检测实验.
选取了几组不同尺寸的图片进行实验,这些图片尺寸在128×128~256×256之间.在相同条件下,采用上面的JPEG Ghost判定标准对图像库中的图片进行双重JPEG压缩和检测实验,若检测到的压缩痕迹与事实一致则标记为检测成功.图2中垂直坐标的频数表示50张图片中被成功检测的数量.从图2(a)和(b)的实验结果来看,DC系数量化误差检测法相较于JPEG Ghost检测法在检测邻近质量因子压缩时有较明显的优势.实验中将综合利用这两种方法进行次Ghost点检测,对比的同时也增加了检测结果的可信度.
去压缩检测算法主要分以下4个步骤.
步骤1 将待检测图像I进行8×8大小的DCT变换,得到的DCT系数矩阵也按照8×8进行分块,记为{B(1,1),···,B(m,n)}.为了简化理论分析的过程,在这里假设原始图像I0(BMP格式)经历压缩时的DCT变换网格对齐.
步骤2 对{B(1,1),···,B(m,n)}综合利用DCT系数直流分量量化误差检测法和JPEG Ghost检测方法进行压缩痕迹检测,并找到次Ghost点(前一次压缩痕迹)αm(对应的量化矩阵Qαm(m<n)).记C为图像所经历过的压缩痕迹的集合,将αm加入到集合C中.
步骤3 对图像I进行“去压缩”.方法是对图像I用步骤2中检测到的量化矩阵Qαm进行一次压缩并保存.
步骤4 将步骤3中得到的“去压缩”后的图像作为新的图像I,重复步骤1~4的检测过程.当检测不到比αm小的次Ghost点时检测结束.
1.3 利用去压缩检测算法对图像进行多重JPEG压缩检测实验
具体针对本文定义的20个质量因子,对不同的图像以及不同的压缩情形进行了大量的实验,在两次质量因子相差大于5%的情况下都有良好的检测效果.这里以图像“Lena”(256×256,BMP格式)为例,用去压缩检测算法进行检测实验.

图2 两种算法的压缩痕迹检测结果对比Figure 2 Comparison of the two methods of the compression traces detection results
将图像“Lena”依次进行质量因子为p=30%,45%,60%,85%(对应量化矩阵Q6,Q9,Q12,Q17)的压缩及保存.提取待检测图像的DCT系数矩阵,综合利用Farid的JPEG Ghost方法及本文提到的DCT系数直流分量误差曲线检测法找到图像依次经历的压缩痕迹.
检测过程及结果如下:

图3 差值分布曲线Figur e 3 Plot of error distribution

图4 去Q 17压缩后的差值分布曲线Figur e 4 Plot of error distribution with Q 17 compression removed

图5 去Q 12压缩后的差值分布曲线Figur e 5 Plot of error distribution with Q 12 compression removed

图6去Q 9压缩后的差值分布曲线Figure 6 Plot of error distribution with Q 9 compression removed
图3 ~6中的(a)图,纵坐标均代表归一化的DC系数误差值的标准差(normalized standard deviation of DC coefficient,NSTD of DC coefficient),图3~6中的(b)图,纵坐标均代表归一化的DCT系数误差值的标准差(normalized standard deviation of DCT coeff icients,NSTD of DCT coefficients),横坐标均对应文中定义的量化矩阵的编号(或质量因子).由图3中的(a)和(b)均可以观察到图像当前经历了量化矩阵Q17的压缩,前一次经历了量化矩阵Q12的压缩,即次Ghost点αm=12.将检测到的压缩痕迹Q17、Q12对应的编号加入集合C.用量化矩阵Q12对待检测图像进行“去压缩”,将图像数据近似恢复到未经量化矩阵Q17压缩前状态.之后,对“去压缩”得到的图像再进行压缩痕迹检测,检测结果如图4中的(a)和(b)所示.根据文中设定的JPEG Ghost判定标准,可找到次Ghost点αm=9.将αm=9加入集合C后,再用量化矩阵Q9对当前图像进行压缩,继续进行压缩痕迹检测,检测结果如图5所示.图5中的(a)检测到了次Ghost点αm=6,而图5中的(b)难以给出类似判断,这也在具体实验中说明了JPEG Ghost检测法在检测邻近质量因子压缩时效果不理想.将αm=6加入集合C后重复类似于前面的检测步骤,检测结果如图6所示,在图6中的(a)和(b)内均检测不到次Ghost点,检测终止.得到了压缩痕迹集合C={6,9,12,17},这与事实一致.
2 利用去压缩检测算法进行多重JPEG压缩篡改检测
为了便于理论分析,不考虑图像在受到篡改过程中经历裁剪处理,假设图片在进行重压缩时前后两次DCT变换网格对齐.将图7(a)中的原始图像(大小256×256,BMP格式)按质量因子40%进行保存.对保存后得到的图像用Photoshop进行局部篡改,在图像中插入“游客”图像块,该图像质量因子未知;之后按照质量因子55%进行保存.假设篡改者后又对篡改区域进行了某些修改和修饰,并将该照片上传到网络服务器中.从整体来看,是在之前基础上又先后对图像进行了质量因子为65%、90%的压缩及保存.篡改检测者从网络服务器中下载得到了待检测图7(b).

图7 图像篡改示意图Figure 7 Diagram of image tampered
将图像转变为灰度值图像(通过分别提取R、G、B三个通道数据进行计算,这里以R通道为例),对图像进行四等分块(实际检测中可适当调整分块的数目,以得到更加准确的检测结果),对每一个分块用文中DCT系数直流分量量化误差检测法进行检测.在图8~10中,纵坐标均代表DC系数误差值的标准差(已归一化),横坐标对应文中定义的量化矩阵的编号(或质量因子).
图8给出了篡改图像整体及各部分的DC系数差值分布曲线.从图8(a)中DC系数差值曲线来看,4个分块均能检测到图像当前质量因子为90%,以及前一次压缩质量因子为65%,与图8(b)整体差值曲线的检测结果相同,此时无法判定图像是否受到了篡改.由于检测到了一致的次Ghost点,即可利用本文去压缩检测算法对图像进行压缩痕迹检测.


图8 篡改图像的DC系数差值分布曲线Figure 8 Plot of DC coefficient error distribution of the tampered image
将待检测图像去除Q18压缩后用同样的检测方法进行检测,可检测到一致的次Ghost点Q11(检测过程同上一致,不赘述).将图像数据近似恢复至刚经过量化矩阵Q11压缩后的状态,进行DCT直流分量量化误差检测,差值曲线分布如图9所示.
综合图9中的(a)和(b)的差值曲线来看,图9(a)中右下方的差值曲线在一定程度上不同于其他3个分块以及整幅图的检测结果.从图中来看检测不到次Ghost点(或程度明显较弱),而根据文中JPEG Ghost判定标准,其余几幅图中除左上方检测曲线次Ghost点相对较弱外,另外两幅都有很明显次Ghost点.根据差值曲线的不一致可初步定位最可疑篡改区域为右下方分块.

图9 去Q 13压缩后篡改图像的DC系数差值分布曲线Figure 9 Plot of DC coefficient error distribution of the tampered image with Q 13 compression removed
为确定右下方分块是否为篡改区域,需要对其进行进一步的细分检测.将可疑区域细分为4个区域重复上面的检测过程,检测结果如图10所示.

图10可疑篡改区域各分块DC系数差值分布曲线Figure 10 Plot of DC coefficient error distribution of each block of the suspected tampered region
图10 是对可疑区域进行分块检测的结果,按位置顺序依次对应图11(a)中各分块的位置.可以发现在图10中,左上分块和左下分块找不到明显的次Ghost点,而右上方和右下方有相对明显的次Ghost点Q8.篡改区域一般是有意义的,从视觉上来看一般出现在一个相对集中的区域.同时,根据误差曲线的不一致可以判定篡改区域为左上和左下分块,定位结果如图11(b)所示(黑色图像块标记处).

图11 篡改区域判定Figure 11 Tampered region localization
3 结语
去压缩检测算法相对于JPEG Ghost检测方法在一定程度上扩展了多重JPEG压缩的检测范围,提高了检测能力,为更进一步的进行图像篡改取证提供了帮助.文中给出了通过去压缩检测算法进行图像篡改检测的可行方案.“去压缩”处理也使得在图像经过了多重压缩后无法利用现有的一些JPEG图像篡改检测方法进行检测或者检测效果差的情况在一定程度上得到了改善.然而该算法针对质量因子非常邻近(如小于5%)的情况检测效果不好,以及在进行图像篡改检测定位时对较小图像块容易产生误判且定位精度不高,还有很多需要继续研究和改进之处.
[1]KEE E,JOHNSON M K,FARIDH.Digital image authentication from JPEG headers[J].IEEE Transactions on Information Forensics and Security,2011,7(3):1066-1075.
[2]FAN J Y,CAO H,KOT A C.Estimating EXIF parameters based on noise features for image manipulation detection[J].IEEE Transactions on Information Forensics and Security,2013,8(4):608-618.
[3]KEEE,O'BRIENJ,FARIDH.Exposing photo manipulation with inconsistent shadows[J].ACM Transaction on Graphics,2013,32(4):1-11.
[4]ABRAMS A,MISKELL K,PLESS R.The episolar constraint.monocular shape from shadow correspondence[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition,2013:1404-1414.
[5]RANG M H,NGUYEN,MINH N L.Light source estimation from a single image[J].International Conference on Control,Automation,Robotics&Vision,2012,5(3):1358-1363.
[6]李叶舟,吴小媚,牛少彰,孟宪哲.基于相机标定的文字变造篡改鉴定[J].北京邮电大学学报,2012,35(6):16-19.
LIYezhou,WUXiaomei,NIUShaozhang,M ENGXianzhe.Forgeries of chinese character detecting based on camera calibration[J].Journal of Beijing University of Posts and Telecommunications,2012,35(6):16-19.
[7]CHIERCHIA G,POGGI G,SANSONE C,VERDOLIVA L.A Bayesian-MRF approach for PRNU-based image forgery detection[J].IEEE Transactions on Information Forensics and Security,2014,9(4):554-567.
[8]RIESS C,ANGELOPOULOU E.Scene illumination as an indicator of image manipulation[C]//12th Information Hiding.Springer Berlin Heidelberg,2010:66-80.
[9]ASATRYAN D,ASATRYAN N,LANINA N.Method for detection of image tampering and partial recovery[C]//Computer Science and Information Technologies(CSIT),2013:1-6.
[10]MUHAMMAD G,AL-HAMMADI M H,HUSSAIN M.Copy move image forgery detection method using steerable pyramid transform and texture descriptor[C]//EUROCON,2013:1586-1592.
[11]JABERIM,BEBISG,HUSSAINM.Improving the detection and localization of duplicated regions in copymove image forgery[C]//18th International Conference on Digital Signal Processing,2013:1-6.
[12]HANY F.Exposing digital forgeries from JPEG ghosts[J].IEEE Transactions on Information Forensics and Security Archive,2009,4(1):154-160.
[13]PUGLISI G,BRUNA A R,GALVAN F.First JPEG quantization matrix estimation based on histogram analysis[C]//20th IEEE International Conference on Image Processing,2013:4502-4506.
[14]GALVAN F,PUGLISI G,BRUNA A R,BATTIATO S.First quantization matrix estimation from double compressed JPEG images[J].IEEE Transactions on Information Forensics and Security,2014,9(8):1299-1310.
[15]LUKÁŠJ,FRIDRICHJ.Estimation of primary quantization matrix in double compressed JPEG images[C]//Processing of Digital Forensic Research Workshop,2003:5-8.
[16]PENG Y,LIU B.Accurate estimation of primary quantization tablewith applications to tampering detection[J].Electronics Letters,2013,49(23):1452-1454.
[17]BIANCHI T,PIVA A.Image forgery localization via block-grained analysis of JPEG artifacts[J].IEEE Transactions on Information Forensics and Security,2012,7(3):1003-1017.
[18]孟宪哲,牛少彰,李叶舟,朱艳玲,胡静.基于双重JPEG压缩特征的数字图像篡改取证技术[J].四川大学学报:自然科学版,2010,47(增刊):225-231.
MENG Xianzhe,NIU Shaozhang,LI Yezhou,ZHU Yanling,HU Jing.Tamper detection based on the statistical characteristics caused by double JPEG compression[J].Journal of Sichuan University:Natural Science Edition,2010,47(Suppl.):225-231.(in Chinese)

