故障条件下子空间预测控制的对偶分解

王建宏， 许 莺， 熊朝华， 徐 波

1.中国电子科技集团公司第二十八研究所，南京210007

2.南京大学天文与空间科学院，南京210093

子空间辨识是通过最基本的矩阵奇异值分解直接将过去和将来输入-输出观测数据序列构成的矩阵进行分解，以得到状态空间方程的各个矩阵式.子空间预测控制来源于子空间辨识，直接从输入-输出观测数据序列中构造将来时刻的输出预测值，而不必根据估计的状态序列重构状态空间矩阵式.

子空间预测控制是一种基于数据驱动的控制方法，能结合系统辨识和预测控制的优点，直接由观测数据构造预测控制中所需的输出预测估计值.文献[1]构造最简单子空间预测控制中的输出预测值，文献[2]比较该输出预测值与迭代相关校正控制下的输出预测值.文献[3]采用经典的椭球优化算法求解无约束子空间预测控制中所出现的目标准则函数的全局最优值，并利用凸分析理论中的水平集构造该优化算法中的初始椭球.文献[4]将子空间预测控制应用于主动噪声的振动抑制，有效地解决了小型直升机悬停状态时的颤振抑l制问题.文献[5]在施加故障的上下限约束条件下，采用快速梯度算法估计故障和设计控制器.

本文对于故障条件下的状态空间方程，根据输入-输出观测数据序列建立故障与残差间的函数关系，并以此建立一个最小二乘优化问题来求解故障估计值.在输出预测估计值的推导形式下分析残差的统计分布性能，并利用矩阵直积的性质推导出残差矢量在瞬时时刻处的结构.将输出预测估计代入预测控制的二次目标准则函数中，考虑一个带有等式和不等式约束的规范化型的二次规划问题.对于较复杂的二次规划问题，提出对偶分解策略，将带有等式和不等式约束的二次规划问题转化为对偶形式下的无约束优化问题，再用迭代梯度算法进行求解.

1 问题描述

考虑如下的随机离散时间状态空间模型：

式中，x(k)∈Rn,y(k)∈Rl,u(k)∈Rm,f(k)∈Rnf分别为状态、输出、控制和故障.矩阵A、B、C、D、E、G、K为恰当维数的实有界矩阵，其中新息e(k)定义为

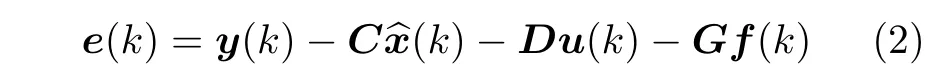
将新息e(k)的定义式(2)代入状态空间模型式(1)可得

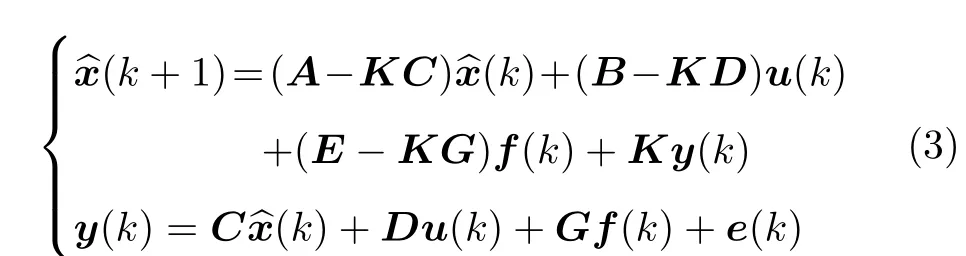
式中，u(k)和f(k)可看作外部的确定性输入信号，当给定期望的输出轨迹时，用期望输出轨迹来衡量式(3)中将来时刻的输出预测值，以最小化量化误差确定控制输入，从而形成预测控制器设计问题[6].设状态、输入、故障输入矩阵分别为

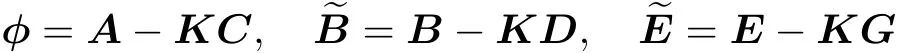
当闭环系统是最小实现时，φ=A-K C是稳定的，且x(k),u(k)和y(k)在任何时刻k都是有界的.

2 故障估计

将状态、输入、故障输入矩阵代入式(3)得

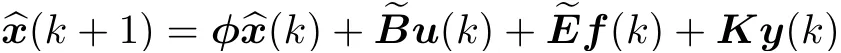
以瞬时刻k-p为初始时刻，递推迭代地求解p个采样瞬时直至时刻k，可得关系式

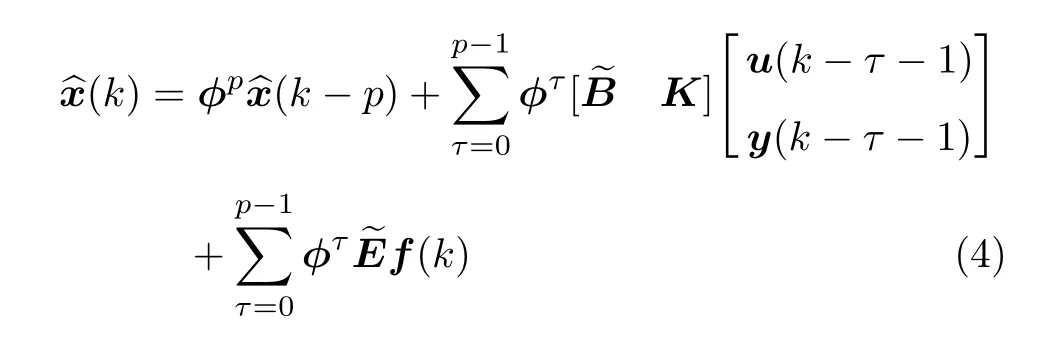
将式(5)代入(4)式可得输出方程的迭代式

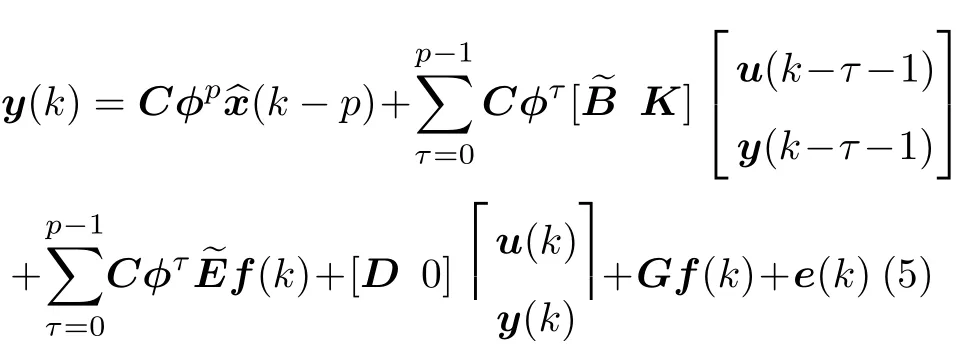
输出方程式(5)被称为外部输入作用下的矢量自回归模型，输出方程式(5)中需要辨识的参数为

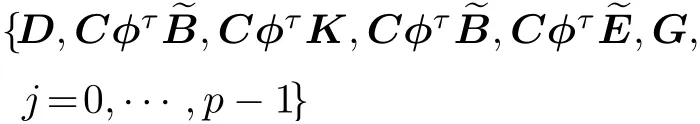
所辨识的马尔科夫参数可由原状态空间模型式(1)通过矩阵运算及所定义的各个矩阵得到.由于转换过程仅仅采用初等矩阵运算，在闭环系统是最小实现条件下的转换过程是唯一的[7].将式(6)中的时间指标k分别用时间序列t,t+1,···,t+N-1来替换，将y(t),y(t+1),···,y(t+N-1)整理成一个块行矢量，记为Yid，即

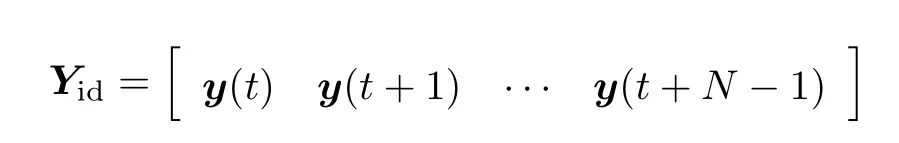
根据式(5)整理矢量Yid中的各个分量，通过计算得到

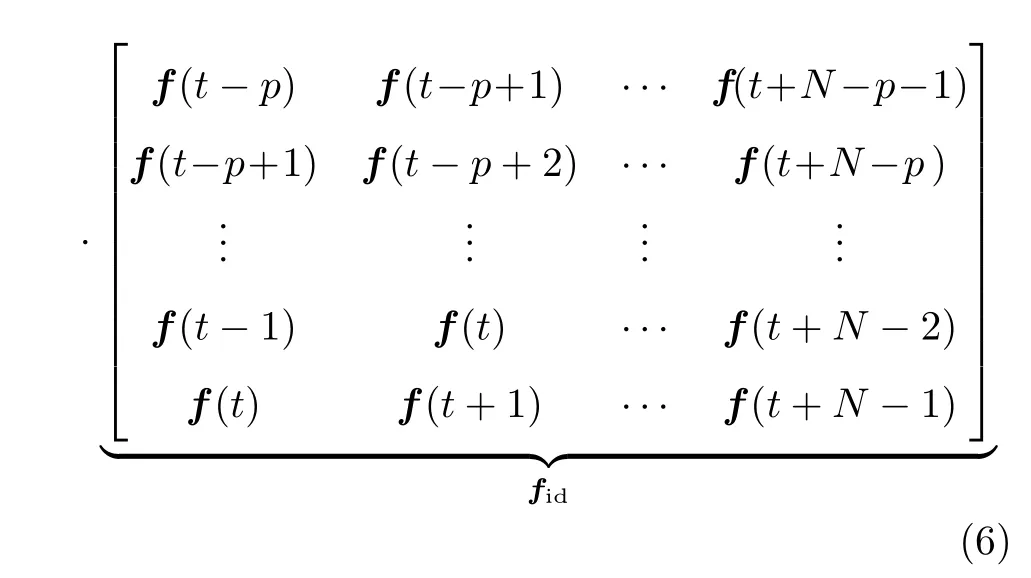
记式(6)中的马尔科夫参数序列分别为

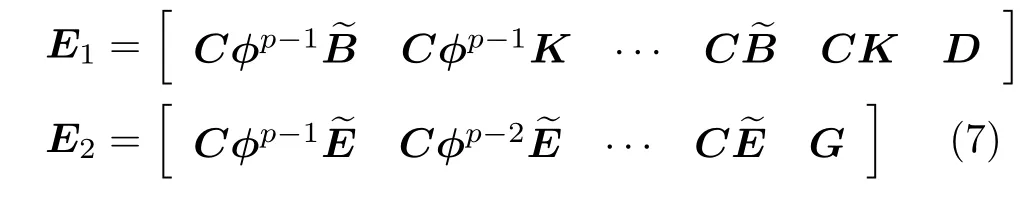
于是可将式(6)简写为

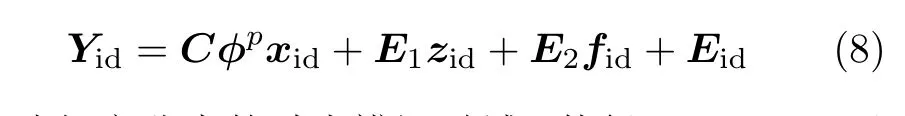
选择充分大的过去辨识时域p使得‖φp‖≈0，于是忽略式(8)的首项未知项Cφpxid，仅剩下近似式

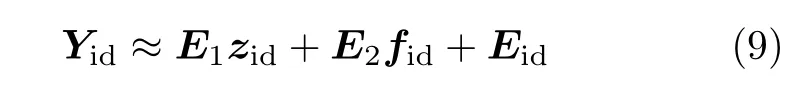
重新整理式(9)，定义残差矢量为

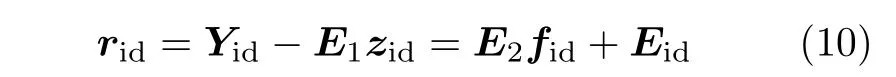
式(10)为故障fid到残差矢量rid间的关系式.对于故障fid的估计可在最小二乘意义下求解，即构成关于故障fid的适定最小二乘优化问题

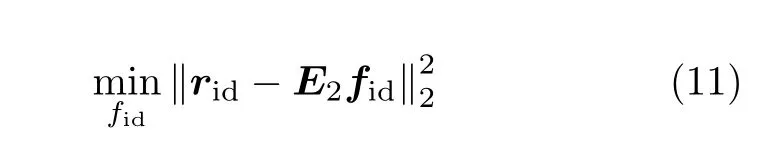
在式(11)中可增加关于故障fid的约束条件，故障fid估计的约束优化问题可采用梯度算法.

3 子空间预测控制下的输出估计

子空间预测控制的首要步骤是给出将来时刻的输出预测值，利用式(5)可计算输出估计.因残差在多于1个采样瞬时的滑窗时域内生成，即滑窗时域为[k-L+1,k]，其中L为输出时域水平.类似地将式(8)的时间指标k分别用L个时间指标来代替，采集y(k-L+1)···y(k)为一列矢量，记为

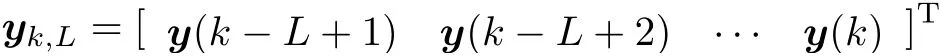
类似地定义块矢量uk,L和ek,L，记[k-L-p+1 k-L]为过去的时域滑动窗，p为过去的时域水平，则输出方程可整理为

记各个块Hankel矩阵分别为

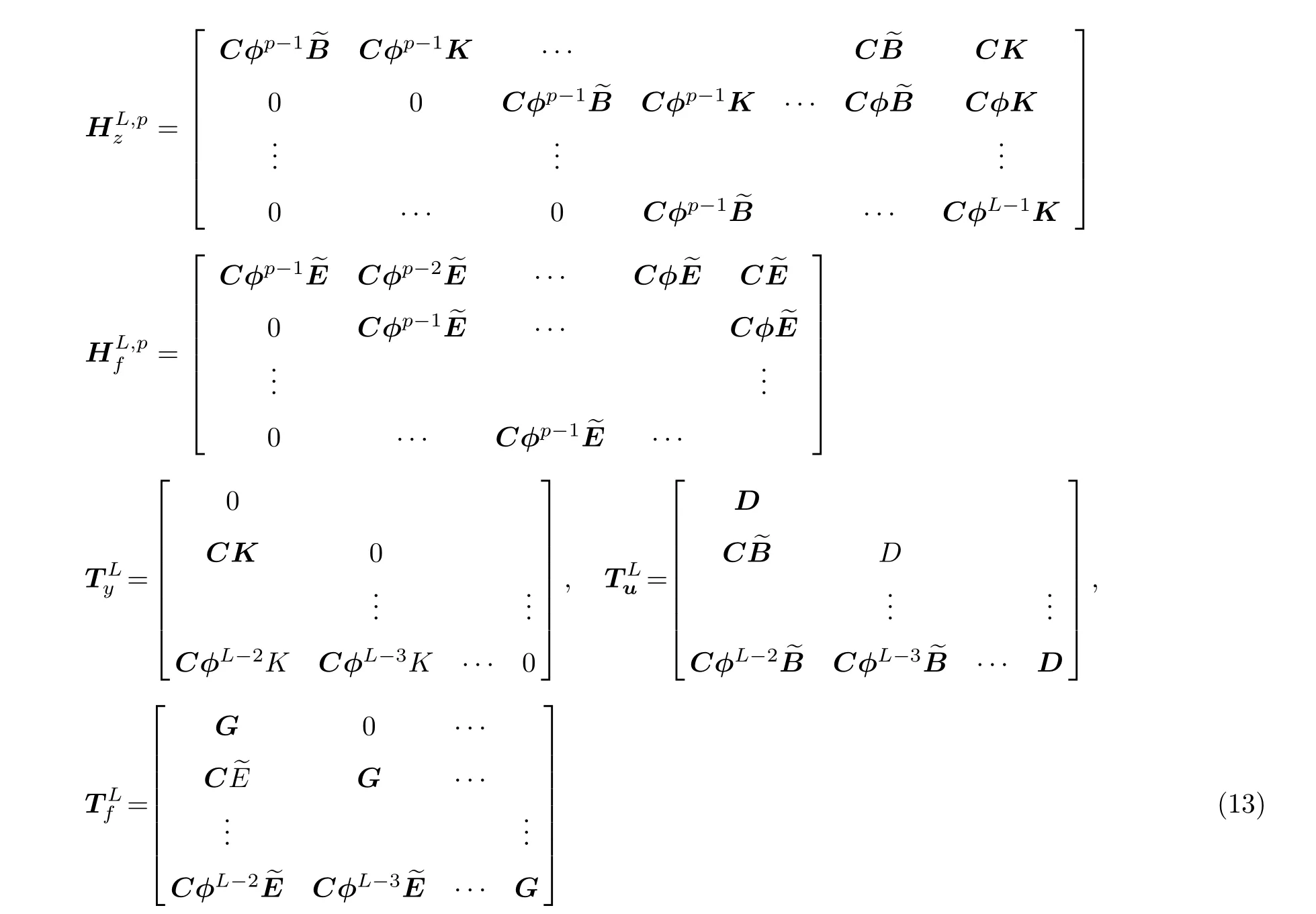
记过去滑动窗下的输入-输出为

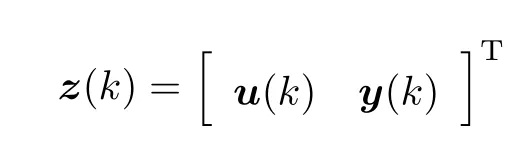
采集过去窗下的块输入-输出观测数据序列为

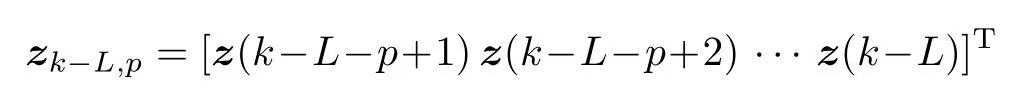
将式(12)简写为紧凑形式为

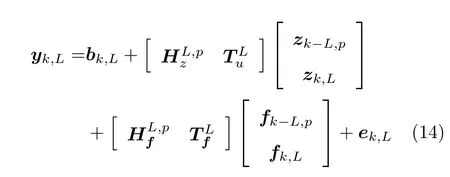
式(14)可改写为

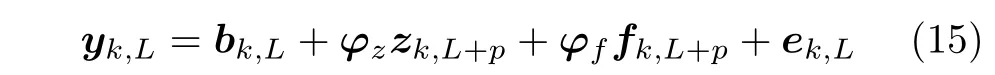
式(15)为子空间预测控制下的输出预测值，但等式右边zk,L+p包含矢量yk,L，故应将该式进行适当的矩阵变换[8]，再代入预测控制的目标准则函数中.

4 残差分析

根据式(15)构造残差矢量为

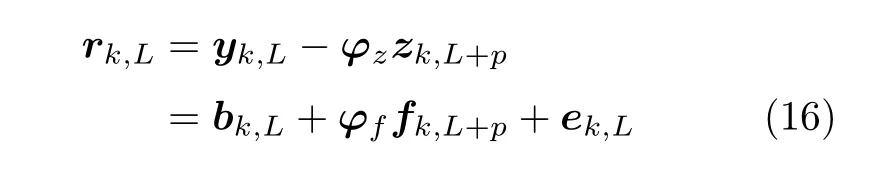
因新息e(k)是白高斯信号，残差rk,L的统计分布为

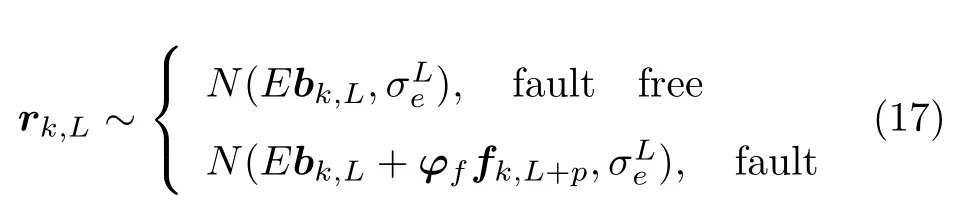
在输出方程式(5)中依次取i=1,···,L,可得

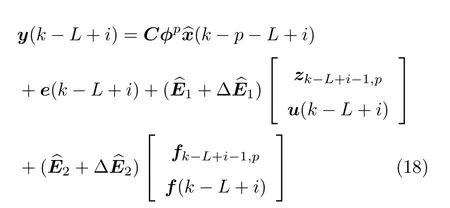
则成立如下关系：

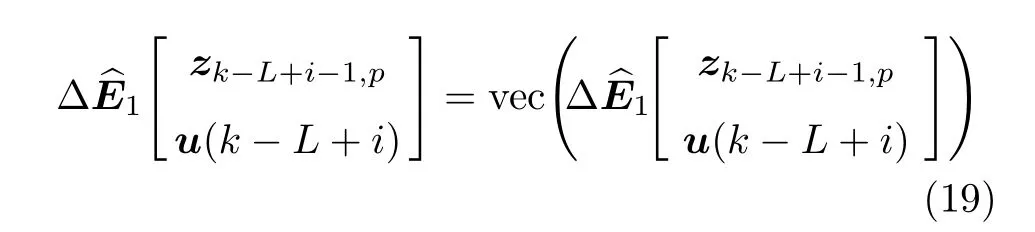
利用矩阵直积的性质[9]有

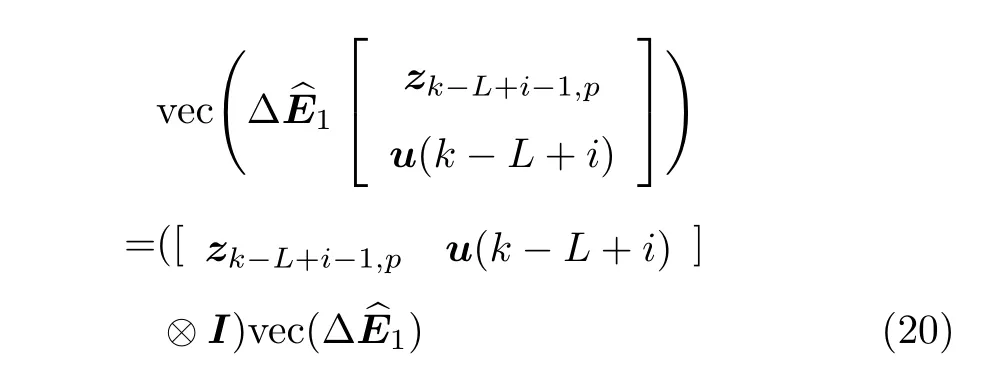
类似有

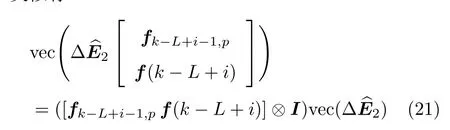
在式(8)的左右两边同乘以伪逆矩阵z+id，得

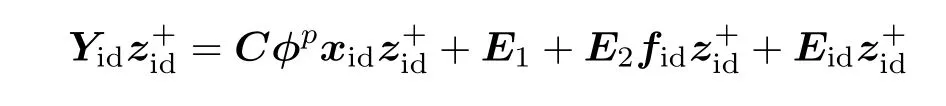
计算马尔科夫参数矩阵E1的误差矩阵为

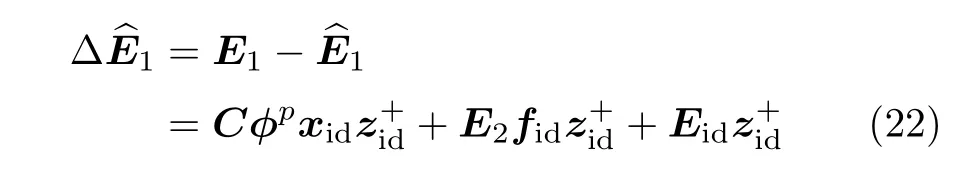
对式(22)取矢量化运算可得

类似有

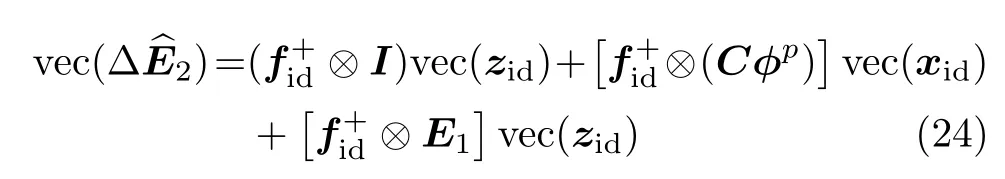
将y(k-L+i)按照i=1,···,L的顺序排列成矢量，利用以上各等式可得

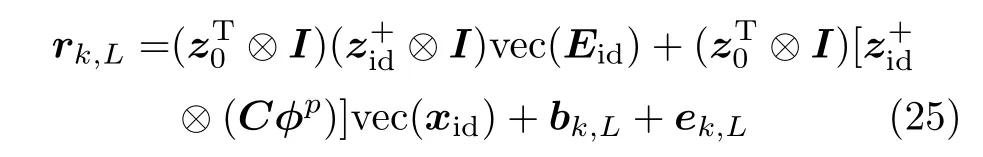
式中，数据矩阵z0可表示为

在残差矢量的推导中，式(17)给出了残差矢量rk,L的统计分布，式(25)给出了rk,L的具体计算结构.

5 子空间预测控制的对偶分解

子空间预测控制中将来时刻控制器输入的求解可回归到一个优化问题的最优解[10].假设期望的输出轨迹序列γ已知，为

预测控制中常用的二次代价性能准则函数为

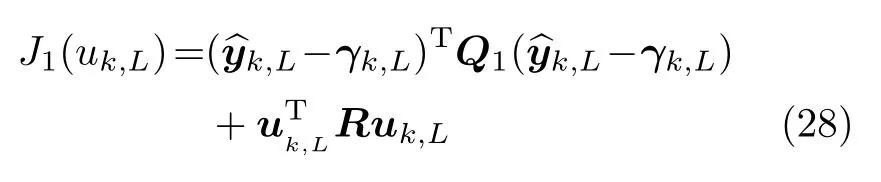
式中，两矩阵Q1和R可选择为对称正定加权矩阵，其中决策变量选择为

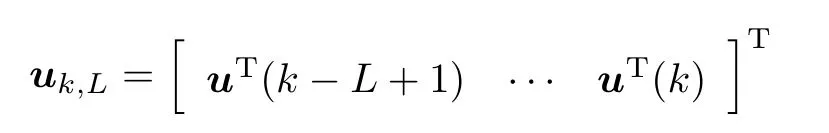
为展开式(28)，需将第1项展开整理成uk,L的显式形式[11].根据式(15)可得将来时刻输出观测数据序列的预测值为

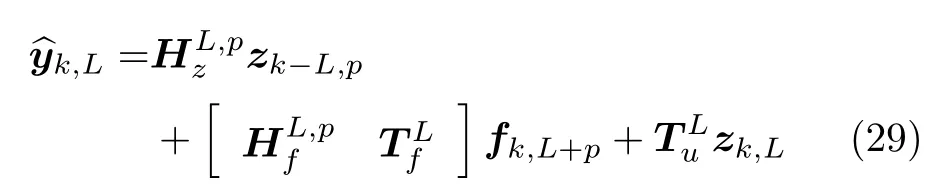
将预测输出值改写为

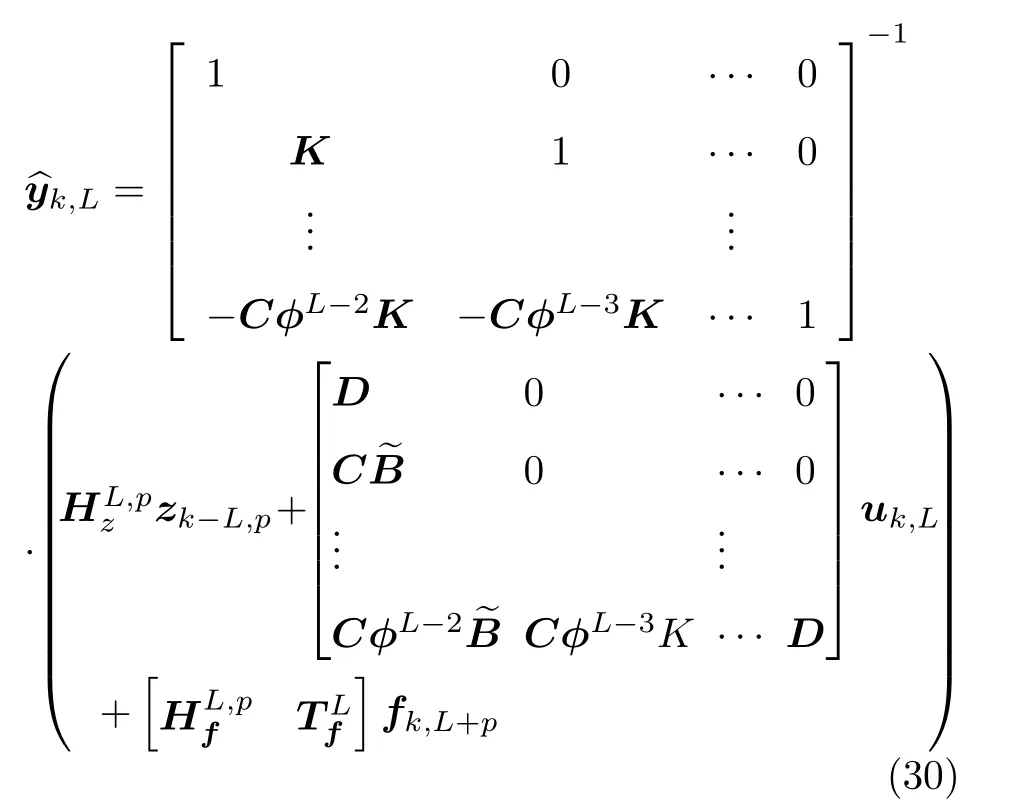
引入3个矩阵来简记式(30)为

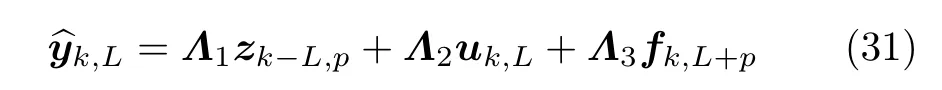
三矩阵Λ1、Λ2、Λ3为zk-L,p、uk,L、fk,L+p前各自的矩阵乘积.将式(31)代入预测控制二次准则函数中，构成优化问题[12]

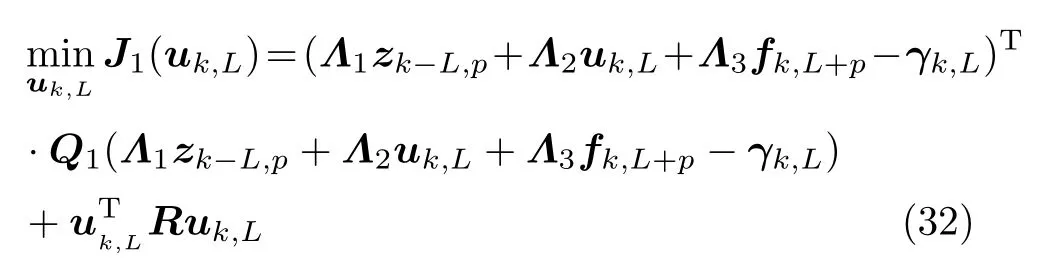
整理式(32)可得

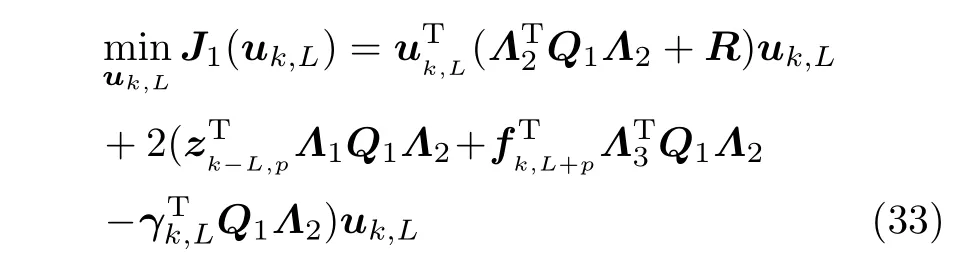
对于式(33)的求解，采用快速梯度算法来解决限制控制输入幅值的特例.对于包含有控制输入uk,L的等式和不等式约束的最优化问题，如果从对偶角度来阐述，就可以通过对偶分解将原约束优化问题转化为一个无约束优化问题[13].将优化问题式(33)改写成

在式(33)中，增加的规范项在于保证决策变量不会发生较大的突变[14]，即构成约束优化问题

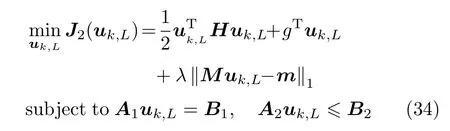
引入拉格朗日乘子矢量µ1、µ2、µ3，构成对偶问题中的拉格朗日函数

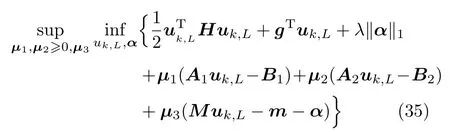
对拉格朗日函数整理可得

先求解关于α的下确界运算得

式中，[]i表示矢量的第i个元素，为求解式(36)关于uk,L的最小化运算，设

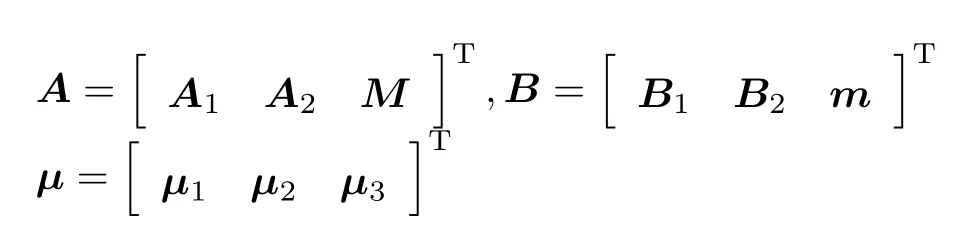
式(36)关于uk,L的最小化运算为

对偶问题为

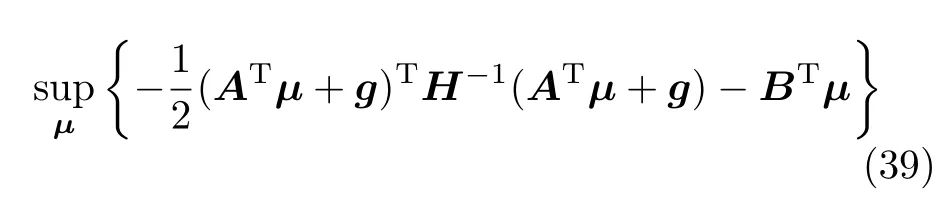
定义负对偶函数为

因为f(µ)包含有正半定海赛矩阵的二次项和线性项，则f(µ)是可微的，其对应的梯度为

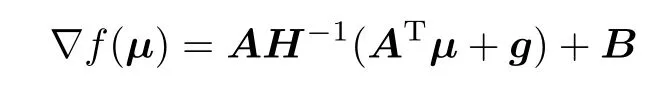
由凸优化理论中的极小-极大定理可知[15]：▽f(µ)的最小Lipschitz常数ζ为

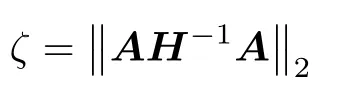
对于偶问题式(39)，用最近邻梯度法可得迭代值

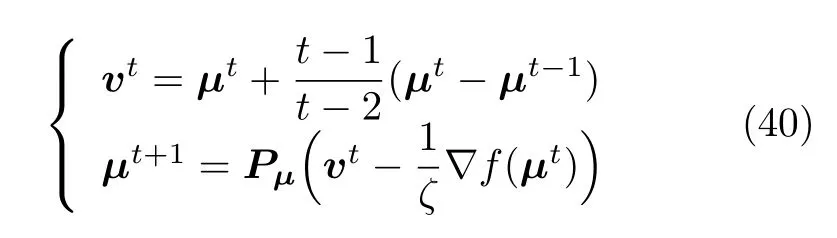
式中，t为迭代次数，Pµ表示µ所在集合上的投影，新迭代值µt+1是在上次迭代值的基础上加上一负梯度投影方向.原优化问题的控制输入迭代值为

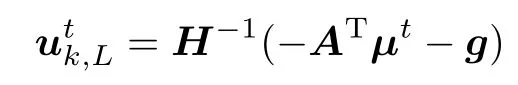
将式(37)中的vt值代入▽f(µ)中得

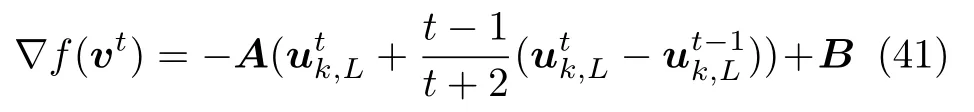
定义

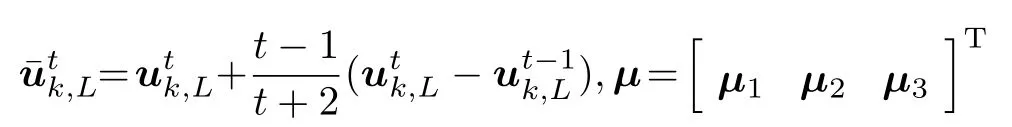
将式(41)并行化处理为

对于等式和不等式约束的最优化问题，虽然对偶迭代求解增加了对偶步骤，但对偶过程将约束优化转化为无约束优化，从而简化了复杂度.

6 仿真算例

以无人直升机在空中的悬停状态为例，采用本文所提出的方法进行预测控制器的设计.仿真时无人直升机带有舵回路和清洗网络的全状态变量模型的各个系统矩阵式分别取为

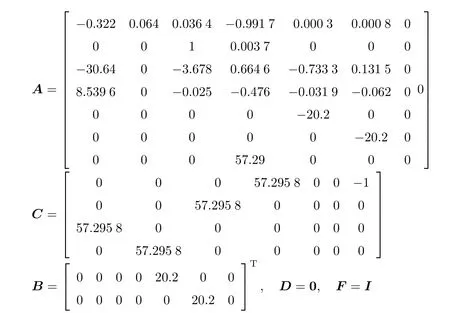
控制输入是方向舵和副翼的伺服输入信号.输出矩阵C中的值57.2958是角度与弧度的转换值.根据系统的状态矩阵A可解出系统的开环荷兰滚模态有极点-0.442 5±j3.063，可见开环荷兰滚的阻尼是不足的，而开环螺旋模态有极点-0.016 31，可采用输出反馈调节器来设计无人直升机的悬停控制.原状态空间系统中过程噪声e(k)为零均值白噪声，其方差矩阵为Ce=10-4I5.预测和控制时域水平分别取为p=L=100.对于加性的截断器故障，常设E=B,G=D=0.故障f(k)的估计可采用最小二乘法来辨识.无人直升机中的加性故障常见于传感器故障和截断器故障，其中的传感器故障并不直接影响无人机的飞行特性，只是传感器在测量过程中所出现的各种由于大气干扰所导致的误差.截断器是针对飞行试验中不可避免地受到大气紊流激励的影响.大气紊流激励作为一种不可测激励，它所产生的随机响应将作为过程噪声包含在测量输出方程中.仿真中取故障估计为

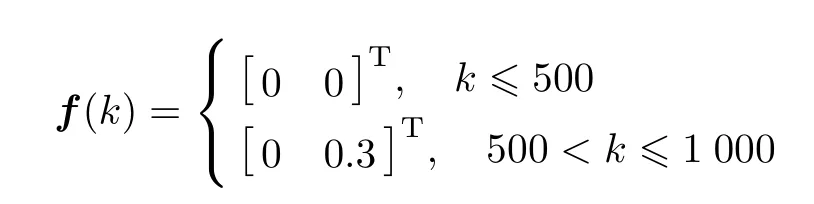
选取3 000个输入-输出采样数据用于闭环试验的预测控制器设计.采样周期取为0.2 s，初始输出反馈控制器选择为

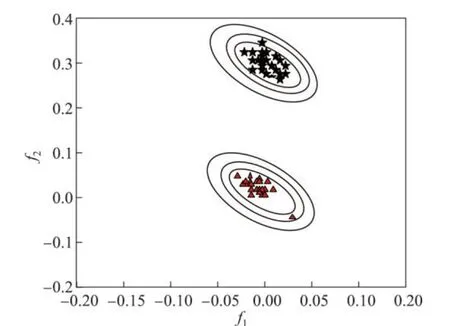
图1 二维故障估计Figure 1 Two dimensions fault estimations

参考信号γ取为零均值的白噪声，其对应的方差为4×10-4I.过去和将来的水平线取为p=60，从而有‖φp‖2≈0，Q1=R=0.01I，等式和不等式约束条件分别取为

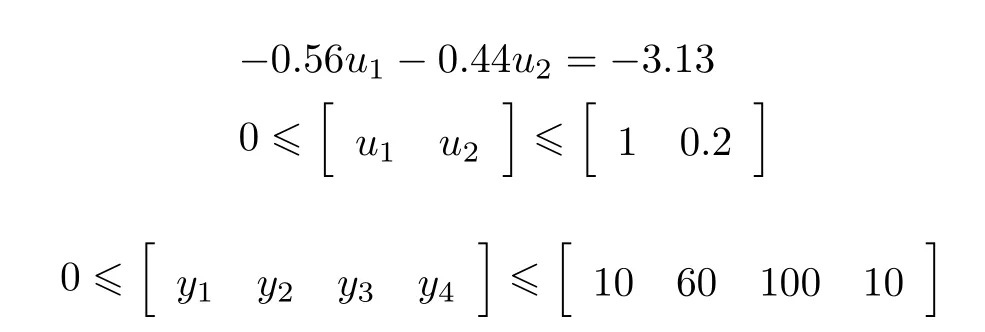
增加的规范项为

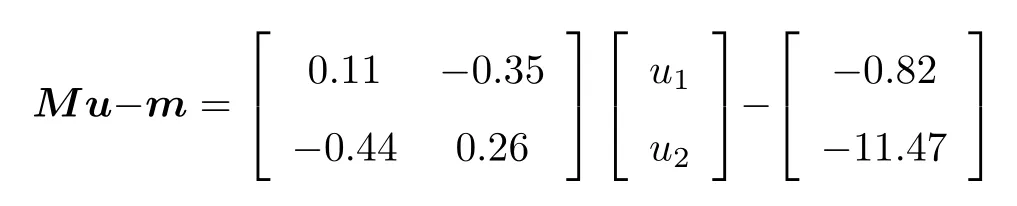
对于子空间预测控制的优化式(34)，采用对偶分解算法求解最优预测控制器.为验证闭环系统性能，系统初始状态选择为x0=10I，利用操纵杆控制无人直升机俯仰姿态的具体过程如下：首先推前飞杆，使直升机向下低头约3°，推杆动作持续3 s后回零位；松杆停5 s，再向后拉前飞杆，使直升机向上抬头约3°，拉杆持续3 s后再回零位，在上述操纵过程下闭环系统的仿真响应曲线如图2所示.无人直升机的姿态角响应和角速率响应均能达到预先期望的轨迹.对操纵杆的控制输入曲线如图3所示，推杆的作用力大小为时变的持续变化力.

悬停状态下进行仿真时，给定悬停点的高空离地面坐标为(-19 m,-83 m),此时无人直升机的航向为197.8°.无人直升机进入悬停状态后，利用指令盘依次发送如下各个指令：前移5 m、右移5 m、后移5 m、左移5 m，各指令发送的间隔均为15 s.利用子空间预测控制器对闭环系统进行输出反馈控制，得到无人直升机位移变化如图4所示.

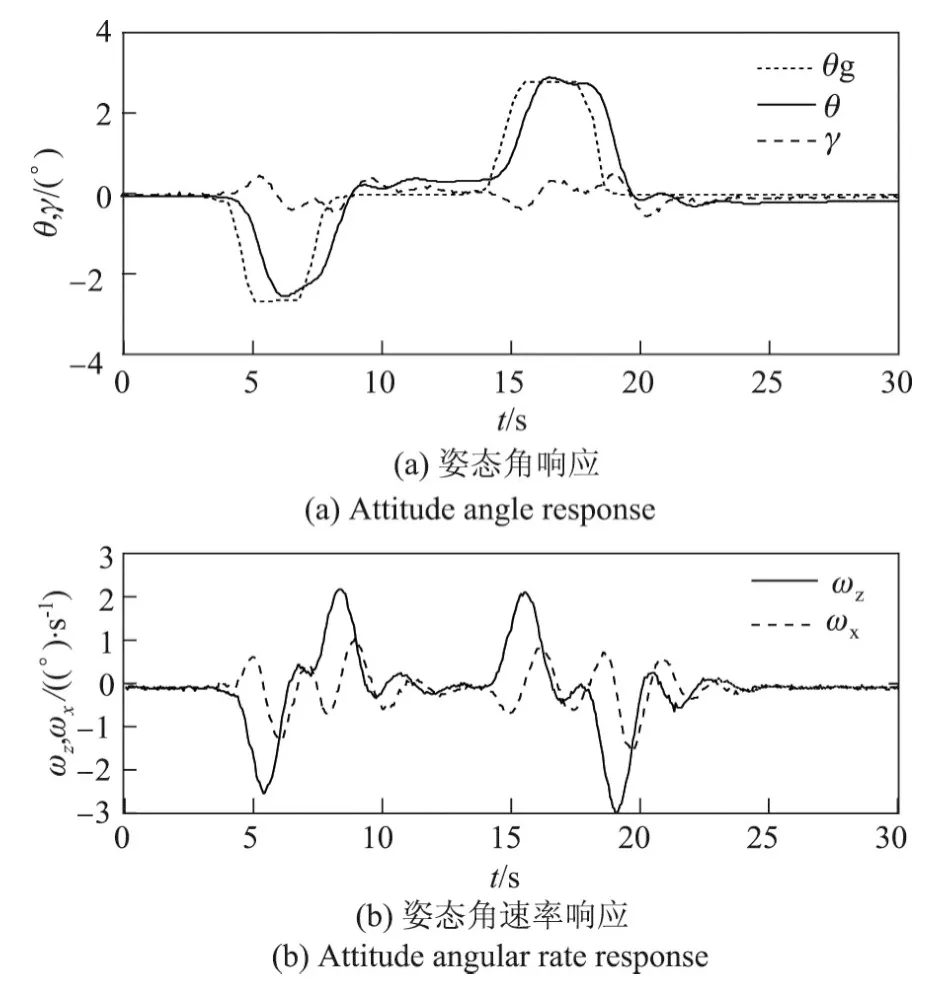
图2 俯仰姿态控制响应曲线Figure 2 Pitch attitude control response curves

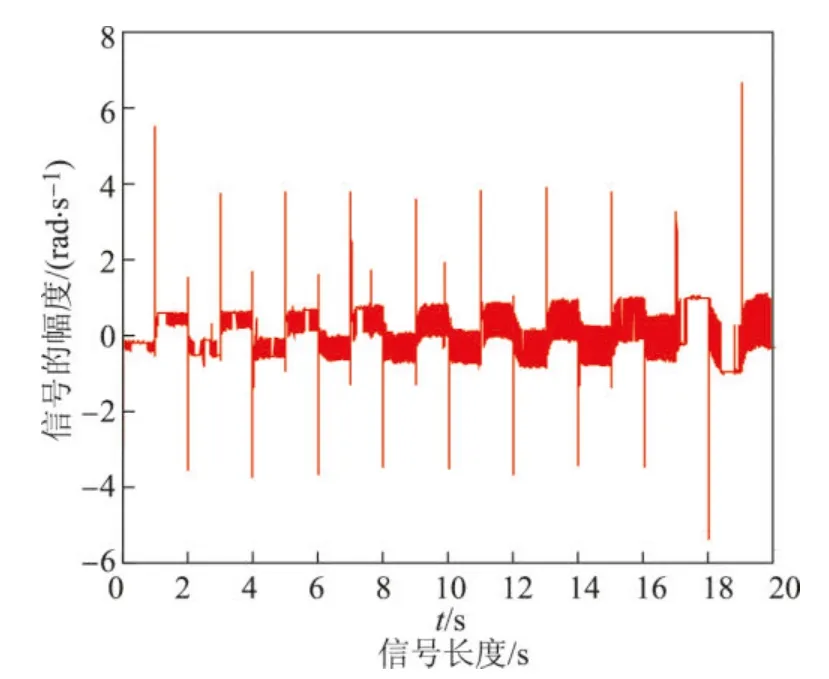
图3 最优控制输入Figure 3 Optimal control input

由图4可得：定点悬停闭环控制在子空间预测控制器的作用下具有良好的控制响应特性，稳态定位偏差小于0.5 m，均符合无人直升机的控制精度要求.前移和后移时，其侧向位移最大值小于0.5 m；左移和右移时，其前向上的位移最大值小于0.5 m，纵向和侧向间的耦合较小.

7 结语

本文研究故障条件下的子空间预测控制问题，推导残差矢量的统计分布具体形式.针对等式和不等式约束的预测控制器最优化问题，通过对偶运算并采用最近邻梯度法即可求解最优的预测控制器.关于算法的渐近性分析是下一步的研究重点.

[1]CHIUSO A.The role of vector autoregressive modeling in predictor based subspace identif ication[J].Automatica,2007,43(6):1034-1048.

[2]CHIUSOA.On the relation between CCA and predictor based subspace identif ication[J].IEEE Transactions of Automatic Control,2007,52(10):1795-1811.

[3]王建宏，王道波.子空间预测控制算法在主动噪声振动中的应用[J].振动与冲击，2011,30(10):129-135.

WANGJianhong,WANGDaobo.Subspace predictive control applied to active noise and vibration control[J].Journal of Vibration and Shock,2011,30(10):129-135.(in Chinese)

[4]王建宏，王道波.子空间预测控制中的椭球优化及其应用[J].应用科学学报，2010,28(4):424-429.

WANG Jianhong,WANG Daobo.Application of the ellipsoid optimization algorithm in subspace predictive control[J].Journal of Applied Sciences,2010,28(4):424-429.(in Chinese)

[5]王建宏.故障估计下子空间预测控制的快速梯度算法[J].上海交通大学学报：自然科学版，2013,47(7):1015-1021.

WANGJianhong.Fast gradient algorithm in subspace predictive control under fault estimation[J].Journal of Shanghai Jiaotong University:Natural Science Edition,2013,47(7):1015-1021.(in Chinese)

[6]LJUNG L.System identif ication:theory for the user[M].[S.l.]:Prentice Hall,1999.

[7]BOYD S,VANDENBERGHE L.Convex optimization[M].UK:Cambridge University Press,2008.

[8]ZEILINGER M.Real time suboptimal model predictive control using a combination of explicit MPC and online optimization[J].IEEE Transactions of Automatic Control,2011,56(7):1524-1534.

[9]JAKOB K.A design algorithm using external perturbation to improve iterative feedback tuning convergence[J].Automatica,2011,47(2):2665-2670.

[10]OHLSSON H.Identif ication of switched linear regression models using sum of norms regularization[J].Automatica,2013,49(4):1045-1050.

[11]Van MULDERSA.Identif ication of systems with localised nonlinearity:from state space to block structured models[J].Automatica,2013,49(5):1392-1396.

[12]FELLERC.An improved algorithm for combinatorial multi-parameteric quadratic programming[J].Automatica,2013,49(5):1370-1376.

[13]FIOERH.Observers for interconnected nonlinear and linear systems[J].Automatica,2012,48(7):1339-1346.

[14]RAKO L.Identif ication of switched linear systems via sparse optimization[J].Automatica,2011,47(4):668-677.

[15]PAUL M J.Identif ication of dynamic models in complex networks with prediction error methods[J].Automatica,2013,49(10):2994-3006.