用于MIMO-OFDM的变换域盲信道估计算法

戴锡平， 彭 华， 郑永军， 王琦峰

解放军信息工程大学信息系统工程学院，郑州450002

结合了多输入多输出（multiple-input multipleoutput,MIMO）技术与正交频分复用（orthogonal frequency division multiplexing,OFDM）技术优点的MIMO-OFDM无疑是一项极具潜力与优势的技术.该技术能充分利用无线信道中的多径效应，提高系统的频带利用率，满足多媒体应用对高速率数据传输的需求，有望成为未来无线通信的候选方案[1].

OFDM技术作为一种多载波调制技术，在数字视/音频广播（DVB/DAB）、互联网接入及下一代无线通信系统中得到了广泛应用.CP-OFDM利用循环前缀消除符号间干扰，以实现频域均衡.然而，在CP-OFDM系统中，数据恢复受信道零点的影响，于是文献[2]用全零后缀（zero padding,ZP）取代循环前缀，并提出了ZP-OFDM系统[2].该系统吸收了CP-OFDM系统的诸多优点，消除了块间干扰，简化了信道估计的难度，降低了均衡的复杂度.

在无线通信系统中，信道估计是当前的研究热点与难点，其性能的优劣直接影响用户数据的检测.有关MIMO-OFDM系统的信道估计已有大量的研究成果.盲信道估计算法因具有较高的带宽增益而得到了广泛应用，其主流算法有：子空间方法[3-4]、线性预测算法[5]、外积分解算法[6]等.子空间算法结构简单，估计精度高，性能优越，但进行估计时通常需要已知信道阶数的精确值.MIMO系统存在许多不同的信道，这些信道可能具有不同的信道阶数，故许多已知的信道阶数检测算法，如MDL、AIC、SS-CMR[7]算法等，不再适用于MIMO系统.由于噪声和舍入误差的存在，几乎不可能获得信道阶数的精确估计.通常可根据先验信息获得信道阶数的上界，因此对信道阶数过估计具有鲁棒性算法的研究有着十分重要的现实意义.在信道阶数过估计的情况下，以文献[8-12]为代表的盲信道估计算法分别实现了对单输入多输出、多输入多输出、MIMO-ZP-OFDM和MIMO-CP-OFDM系统信道的盲估计，其中文献[10-11]均用时域子空间算法来估计信道，通过对算法中矩阵结构以及解空间之间的关系进行相关性研究，克服了子空间算法对信道阶数过估计比较敏感的缺点；文献[12]分离出连续两个接收符号块的互相关矩阵中所包含的信道信息，进而提出了一种基于预编码的子空间算法.本文则对文献[13]的算法进行推广，提出了一种适用于MIMO-ZP-OFDM的子空间方法.该算法将变换域方法[14]与子空间方法相结合，降低了噪声对系统性能的影响，提高了算法的估计精度，且对信道阶数具有很强的鲁棒性，

1 M IM O-OFDM系统模型

在频率选择性衰落信道下，考虑一个具有Nt根发射天线和Nr根接收天线的单用户MIMO-ZP-OFDM系统.设OFDM的子载波数目为M，补零后缀长度为Lzp，第p根发射天线与第q根接收天线之间的时域信道响应为hqp，信道阶数为Lqp，且具有Lqp≤L，L表示信道阶数的上界.考虑信道阶数过估计情况，在hqp尾部添加L-Lqp个0，使得各天线对之间的时域信道响应hqp具有相同的长度，即

在发送端，频域子数据流经过OFDM调制后变成Nt列并行传输的时域子数据流sp(n)=[sp(n,0),sp(n,1),···,sp(n,M-1)]T(p=1,2,···,Nt)，插入长度为Lzp的ZP后，经串并转换在Nt根发射天线上独立传输.

经无线信道传输后，接收端第q根接收天线在第n个接收时刻第k个子载波上的接收信号可表示为

式中，ηq(n,k)是均值为0、方差为σ2的复加性高斯白噪声，符号“*”表示线性卷积.不同于CP-OFDM系统，在接收端对接收信号进行FFT之前，无需去除ZP-OFDM系统中的保护间隔.令N=M+Lzp，则对每个接收符号块的N点采样进行FFT变换后，频域的接收符号块可表示为

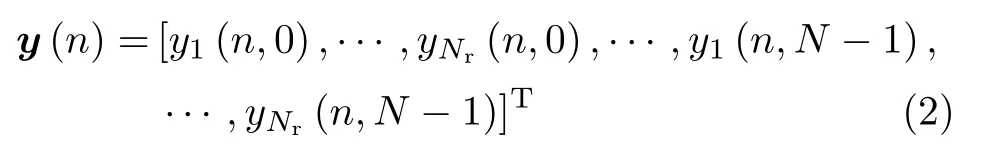
在ZP-OFDM系统中，因插入ZP而消除了块间干扰，于是可将式(1)中的线性卷积等效为sp(n,k)与hpq(k)的N点循环卷积，即对式(1)的两端进行FFT变换

式中，Hqp(k)、Sp(n,k)、(n,k)分别为信道的频域冲击响应、发送信号sp(n,k)、噪声ηq(n,k)的频域采样. 定义N阶归一化Fourier变换矩阵W，元素[W]qp=e-j2π(q-1)(p-1)/N/，令ϖ=WN×M⊗INt，WN×M表示矩阵W的前M列，INt表示Nt×Nt维单位矩阵，⊗表示Kronecker积，则根据式(3)可将MIMO-ZP-OFDM系统的输入输出关系用矩阵表示为

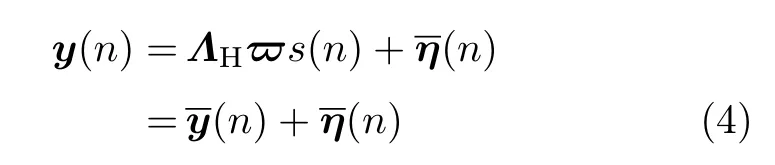
式中，各符号定义如下：

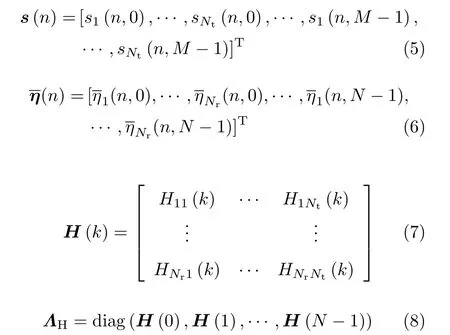
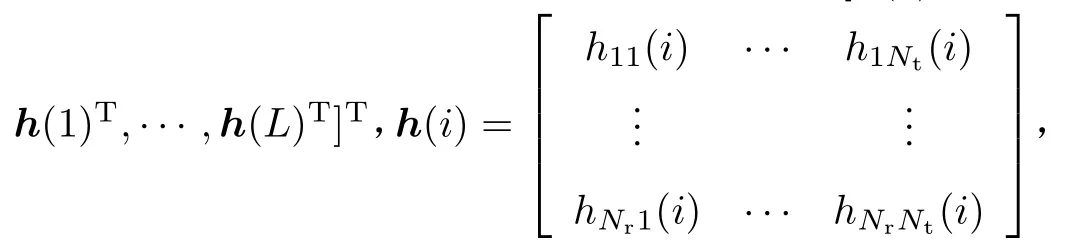
则H=DFTN{h}，其中DFTN{·}表示N点的块DFT变换，因此需要估计的真实信道即为h.

2 频域子空间与变换域联合估计算法

2.1 频域子空间估计算法

该部分主要对频域子空间盲信道估计算法进行研究，即根据频域观测信号y(n)，利用观测信号的二阶统计量对真实信道=[H(0)T,H(1)T,···,H(N-1)T]T进行盲估计.为了使信道可辨识，假设信道矩阵ΛH为列满秩矩阵，且发送信号sq(n,k)和信道噪声ηq(n,k)的统计特性满足以下条件：

1)噪声为复高斯白噪声且相互独立，即

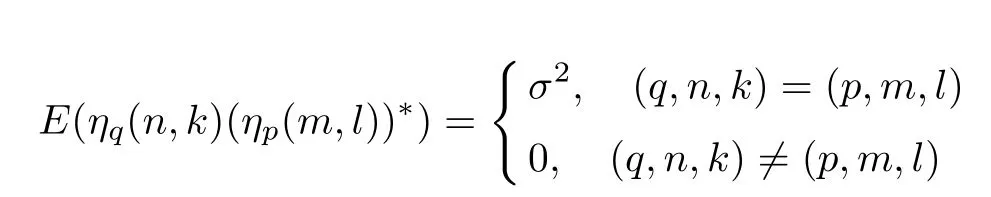
2)噪声与发送信号互不相关，即E(sq(n,k)·(ηp(m,l))∗)=0.

引入y(n)和s(n)的自相关矩阵Ry=E{y(n)y(n)H}和Rs=E{s(n)s(n)H}，根据式(3)所定义的系统模型及假设条件可得

对自相关矩阵Ry进行特征值分解，并按照特征值的大小进行排序，则Ry可表示为

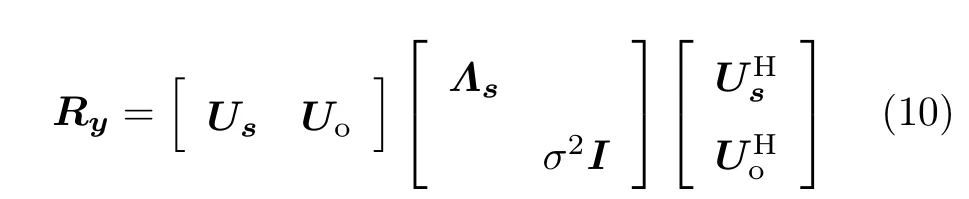
式中，Λs为NtM×NtM维对角矩阵，矩阵Us与Uo的列向量所张成的空间分别为自相关矩阵Ry所对应的信号子空间与噪声子空间.由式(10)可知，Ry的最小特征值为σ2，由于rank=NtM，则存在k=NrN-NtM个相互正交的与最小特征值σ2相对应的特征向量ui(i=0,1,···,k-1).由于N＞M，当Nr≥Nt时，k＞0.因此，该方法适用于接收天线数不少于发送天线数的情况.

由子空间理论可知

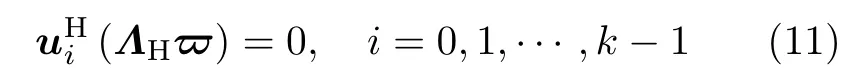
将噪声特征向量ui分割成N个小块，每个小块为Nr×1维列向量，如式（12）所示：

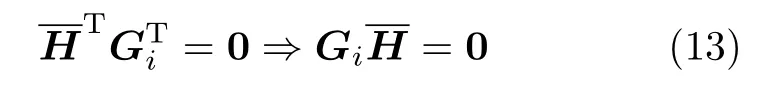
定义k M×NrN维矩阵由式(13)可知=0，信道矩阵的列向量属于矩阵G的右零空间.由文献[10]可得矩阵G右零空间的维数为Nt，于是对矩阵G进行特征值分解，其零特征值所对应的特征向量即为真实信道的估计值.但在实际应用中，由于噪声和舍入误差的存在以及接收信号自相关矩阵估计的不准确性，式(13)很难得到满足，大多通过求解代价函数的最小值来估计信道.首先建立如下的代价函数：

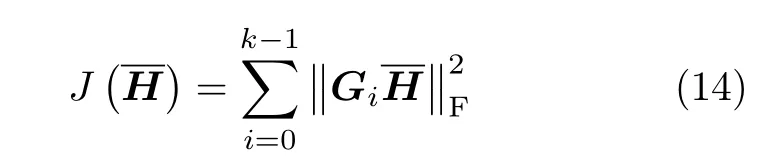
式中，‖·‖F表示Frobenius范数.为了避免出现零解，在=1的约束下，信道矩阵H的最小二乘估计为

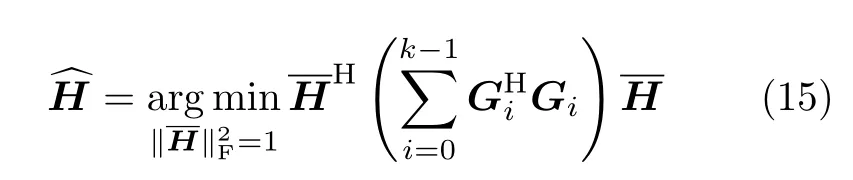
根据式(15)对本文进行信道估计，在范数约束下求解最优解问题.矩阵最小的Nt个特征值所对应的特征向量即为信道矩阵最小二乘估计，这与传统的基于二阶统计量的盲估计算法类似，其真实值与估计值之间存在模糊度问题，即

式中，Ω是Nt×Nt维可逆矩阵，表示盲估计算法的模糊度.对盲估计算法中存在的模糊度问题，常利用少量导频序列加以消除.

2.2 基于DFT的估计算法

考虑由式(3)所示的Nb组观测数据

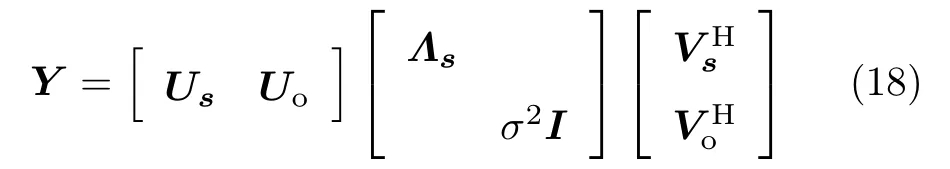
由于受噪声的影响，噪声子空间Uo的一阶扰动近似表示为[15]真实信道矩阵H的一阶扰动近似具有如下形式[11]：

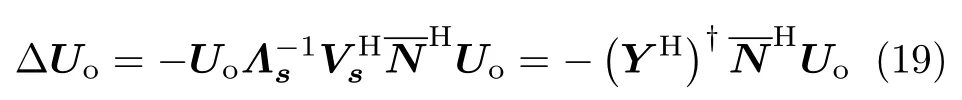
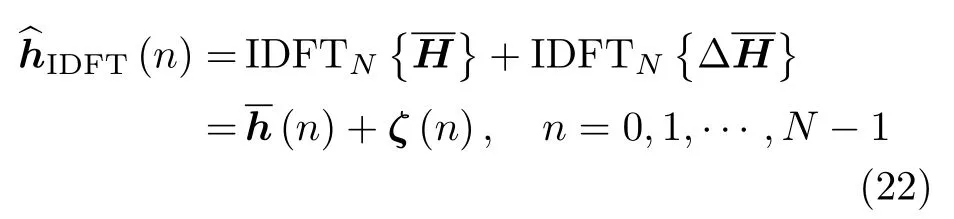
式中，IDFTN{·}表示N点的块IDFT变化，表示信道的实际冲击响应.当0≤n≤L时，(n)=h(n)；当n＞L时，(n)=0.ζ(n)表示时域响应中的噪声分量.由式(22)可以看出，信道估计值因受噪声影响而偏离真实值.当n＞L时，(n)=ζ(n)，信道的时域估计只存在噪声分量.从理论上来说，OFDM信号周期一般远大于信道时域冲击响应的持续时间，经IDFT变化之后，时域冲激响应的全部能量应集中于开始的少数几个点上.设信道估计值为L，保留路径长度为L，提取前L个采样点而忽略噪声采样点得到的时域估计可表示为

3 性能分析

为了评价本文所提出的盲信道估计算法的优劣，下面对信道估计问题的克拉美罗界进行分析.盲信道估计是一个不可辨识问题，常与某种形式的约束相结合，以克服不可辨识性.对信道矩阵进行范数约束，排除了采用传统的CRB方法，故本文主要对约束估计的CRB进行分析，考虑最小约束的CRB[16].

与WN×M类似，设WN×(L+1)为矩阵W的前L+1列，ϖL=（WN×(L+1)⊗INr），vec(·)为向量化算子，(·)†表示矩阵的伪逆，trace(·)表示矩阵的迹.

令

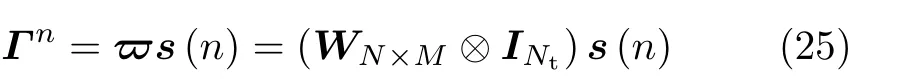
令

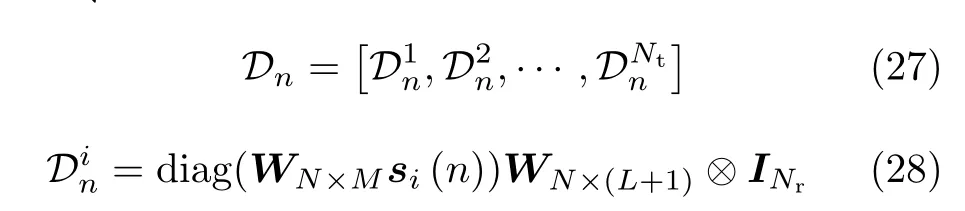
则由式(3)、式(25)、式(27)可得

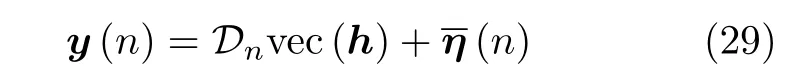
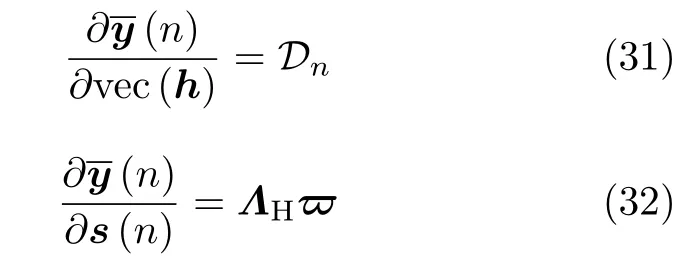
定理1[16]考虑，Fisher信息矩阵可表示为

假定J奇异，而J22非奇异，则关于vec(h)的最小约束CRB可表示为

在所有的约束中，式(34)给出了trace(CRBvec(h))的最小值.

令A=ΛH(WN×M⊗INt)，由定理1可得

对于Nb个观测样本，关于的最小约束CRB为

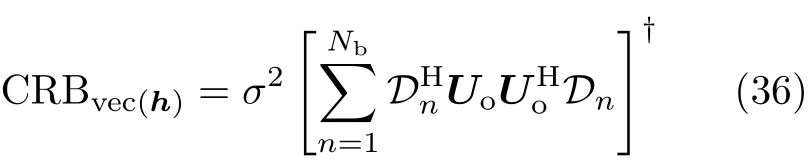
由于

式中，1Nr表示Nr×Nr维的全1矩阵，⊙表示Hadamard积.因此，将式(36)代入式(35)可得vec(h)的最小约束CRB为

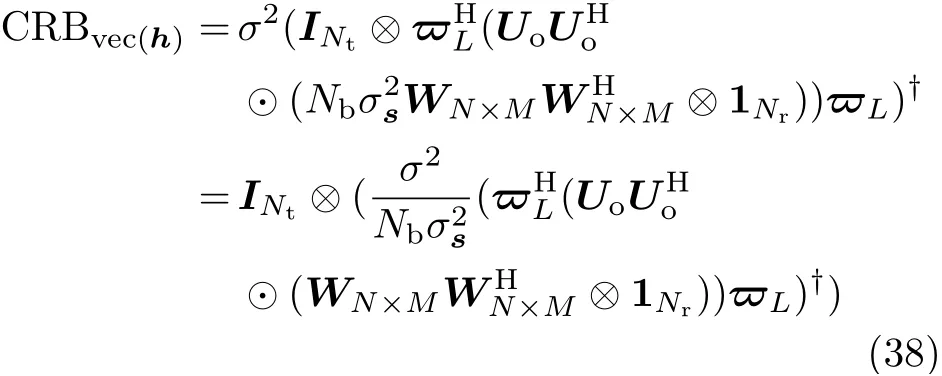
4 理论分析与仿真结果

下面对本文算法的性能进行仿真验证，仿真中采用2发3收的MIMO-ZP-OFDM系统.子载波数目M=32，ZP的长度为Lzp=8，信道阶数为4，观测样本数据长度Nb=300.系统采用QPSK调制方式，无线信道采用准静态的频率选择性衰落信道，各信道抽头系数独立同分布，服从复高斯分布且噪声是空间不相关的、均值为0、方差为σ2的复高斯白噪声.为了评价算法性能，选用均方误差作为系统的评价指标

式中，Nm为蒙特卡罗仿真次数.仿真时进行100次蒙特卡罗实验，^h和h分别表示信道响应的估计值与真实值.

为了验证本文算法对信道阶数的过估计具有很强的鲁棒性，在真实信道阶数为4阶的情况下，假设估计的信道阶数分别为4、6、8，L=6,L=8表示对信道阶数的过估计.假定观测样本长度Nb=300或SNR=30 d B，信道阶数过估计情况下信道估计的均方误差和CRB随信噪比和观测样本数据长度的变化情况分别如图1和2所示.容易看出，信道阶数的过估计仅造成轻微的性能损失.对于ZP-OFDM，在观测样本数据长度较小或低信噪比情况下，频域子空间方法的估计精度与CRB相距较大，随着信噪比的提高或观测样本数据长度的增加，估计的均方误差迅速逼近CRB，说明仿真结果能够很好地符合理论结果.

当观测样本长度Nb=300，L=6，SNR=15d B和20 d B时，比较信道抽头系数幅度的估计值与真实值，结果分别图3中的(a)和(b)所示.显然，当SNR=15 d B时，算法的估计性能较差，估计值与真实值之间差距较大；随着信噪比的增加，当SNR=20 d B时，大大提高了算法的估计精度，估计值迅速向真实值靠拢.

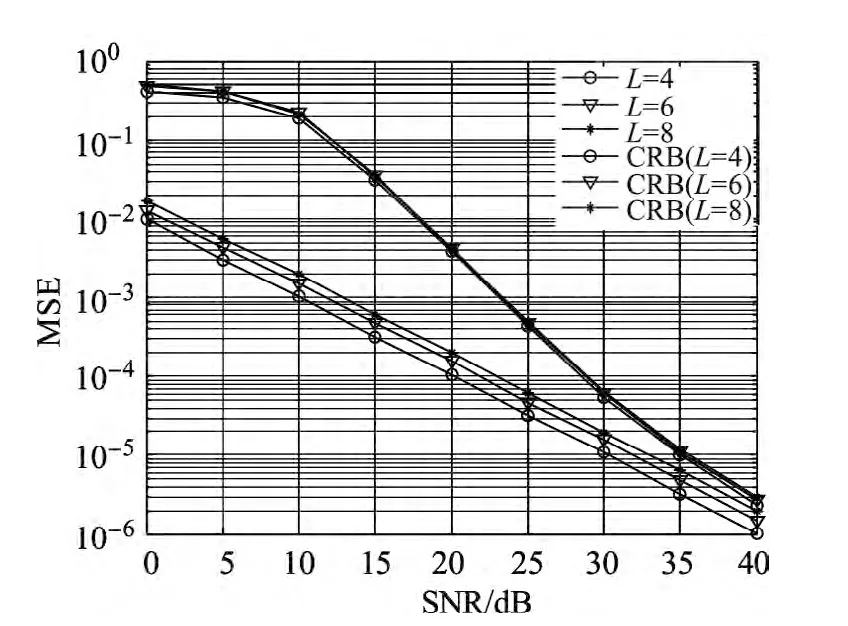
图1 MSE与CRB随SNR的变化曲线Figure 1 MSE and CRB curve with the change of SNR

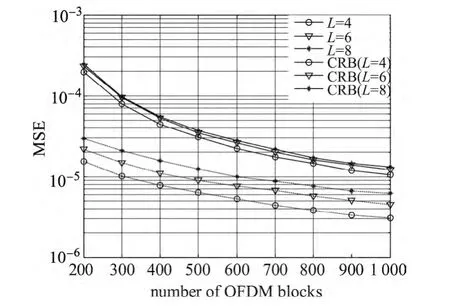
图2 MSE与CRB随N b的变化曲线Figure 2 MSE and CRB curve with the change of number of OFDM blocks

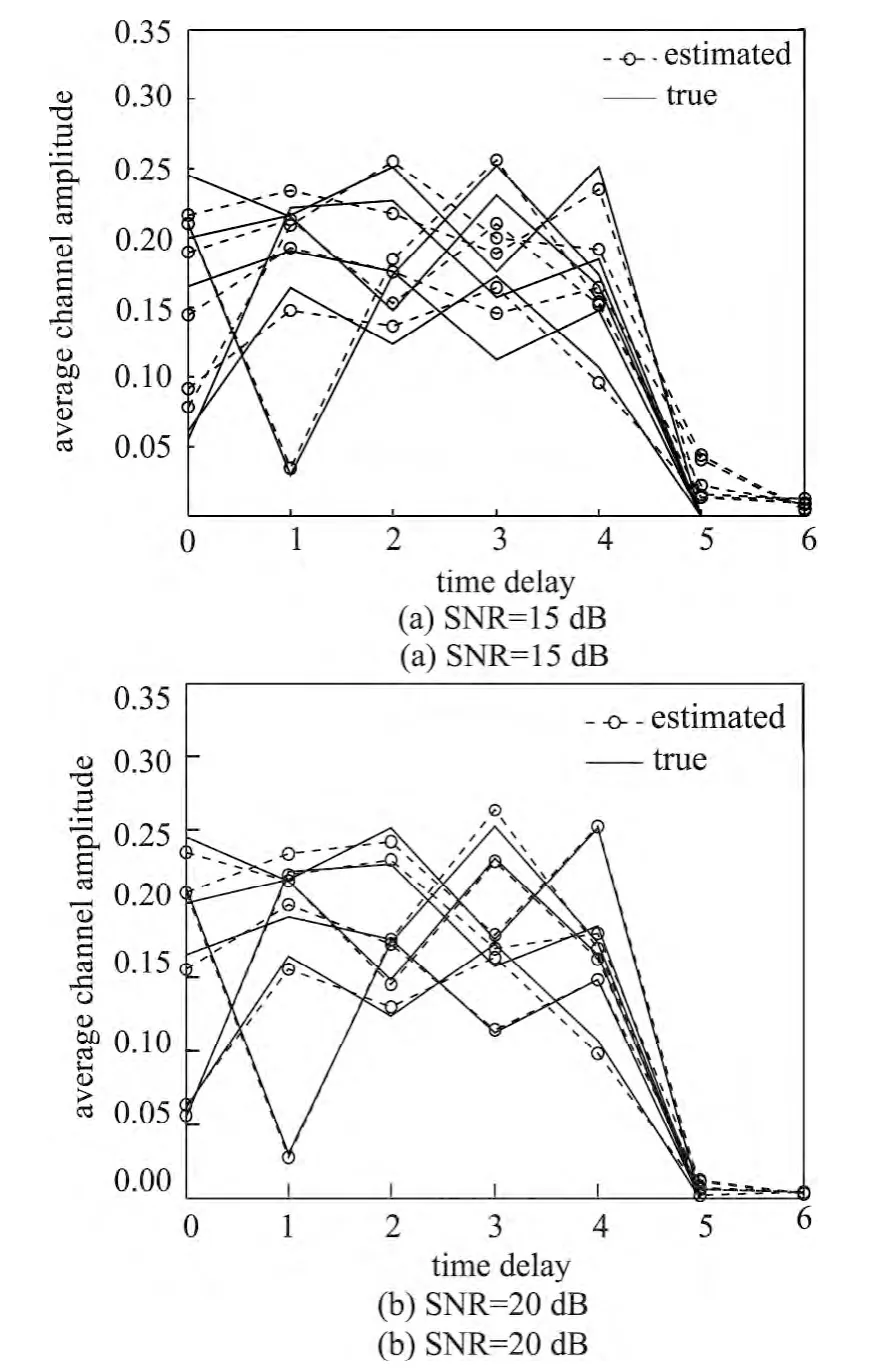
图3 信道抽头系数幅度的估计Figure 3 Amplitude estimation of channel taps

从图3中的(a)和(b)中均可以看出，第5和6抽头的抽头系数几乎为零，从而验证了本文算法适用于信道阶数过估计.

当L=6时，4种算法的估计性能随信噪比的变化情况如图4所示.在信道阶数过估计条件下，各算法均能精确估计信道信息.从图4中可以看出，与文献[10-11]所提出的算法相比，本文算法略优于其他两种算法.与文献[12]所提出的算法相比，本文算法尽管在低信噪比条件下的性能较差，但随着信噪比的增加，尤其是当SNR大于20 d B时，本文算法明显优于文献[12]所提出的算法.本文将DFT算法与子空间算法相结合，将CIR之外的采样点视为噪声并置为零，因此降低了噪声的影响，提高了算法的估计精度.

假设在已知真实信道的情况下，使用真实信道和估计信道对MIMO-ZP-OFDM系统进行频域迫零均衡.图5比较了两者的误比特率性能，给出了两者的误比特率性能随信噪比的变化情况.在低信噪比条件下，信道估计精度较低，两者误比特率性能差距较大；随着信噪比的增加，信道估计精度逐渐增加，使用信道估计值进行频域迫零均衡得到的BER逐渐接近使用真实信道进行频域迫零均衡得到的BER，这在高信噪比下尤为明显.

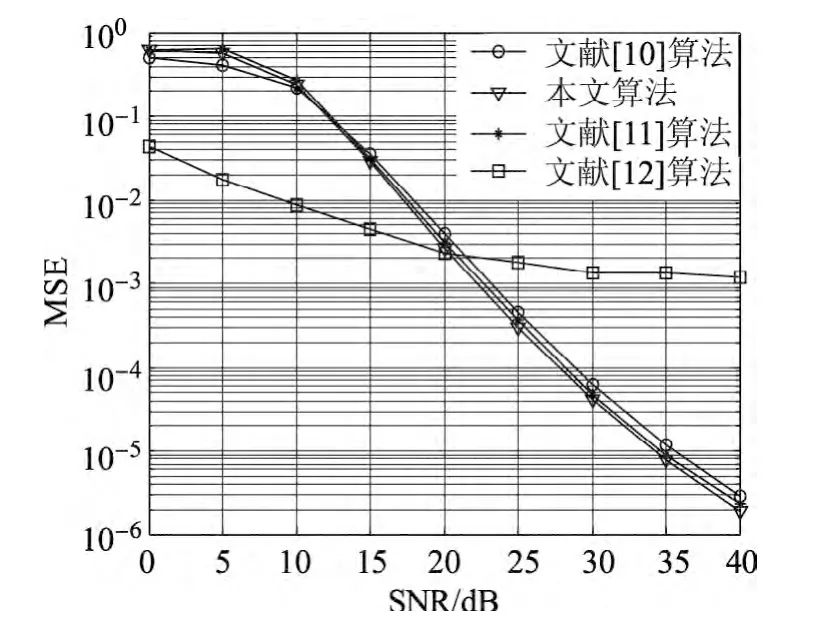
图4 4种算法的MSE随SNR的变化曲线Figure 4 MSE curve of four algorithms with the change of the SNR

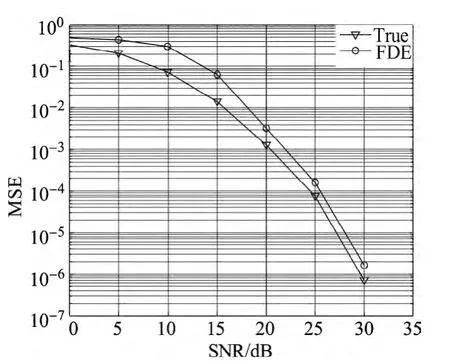
图5 BER随SNR的变化曲线Figure 5 BER curve with the change of the SNR

5 结语

针对MIMO-ZP-OFDM系统，本文提出了一种基于频域子空间盲信道估计方法，简要地描述MIMOZP-OFDM的系统模型，给出了该系统模型的矩阵表达式，从理论上分析了盲信道估计的性能界，推导了该方法的最小约束CRB.理论分析与仿真结果表明，该方法在信道阶数过估计的情况下仅造成轻微性能损失，对信道阶数的过估计具有很强的鲁棒性，能够在接收天线数不少于发送天线数的情况下估计信道，且信道估计的精确度、误比特率性能及其对应的CRB与观测样本的长度和信噪比息息相关.

[1]SAMPATH H,TALwAR S,TELLADO J,ERCEG V,PAVLRAJ A.A fourth generation MIMO-OFDM broadband wireless system:design,performance and field trial results[J].IEEE Communications Magazine,2002,40(9):143-149.

[2]MUQUET B,WANG Z,GIANNAKIS G B,de COURVILLE M,DUHASMEL P.Cyclic-pref ix or zeropadding for multicarrier transmissions? [J].IEEE Transactionson Communication,2002,50(12):2136-2148.

[3]TUC C,CHAMPAGNEB.Subspace-based blind channel estimation for MIMO-OFDM systems with reduced time-averaging[J].IEEE Transactions on Vehicular Technology,2010,59(3):1539-1544.

[4]PANY,PHOONGS.An improved subspace-based algorithm for blind channel identif ication using few received blocks[J].IEEE Transactions on Communications,2013,61(9):3710-3720.

[5]DE P,CHANG T H,CHI C Y.Linear prediction based semiblind channel estimation for multiuser OFDM with insufficient guard interval[J].IEEE Transactions on Wireless Communications,2009,8(12):5728-5735.

[6]GAO Chengzhi,TAI Ludong,ZHUANG Jiaping.Underwater acoustic channel blind identif ication based on matrix outer-product decomposition algorithm[C]//IEEE International Congress on Image and Signal Processing,2009:1-4.

[7]孙有铭，刘洛琨，崔波，郭虹.基于子空间信道矩阵迭代的阶数估计算法[J].电子与信息学报，2013,35(2):432-437.

SUN Youming,LIU Luokun,CUI Bo,GAO Hong.Channel order estimation algorithm based on subspace channel matrix recursion[J].Journal of Electronics&Information Technology,2013,35(2):432-437.(in Chinese).

[8]GAZZAH H,REGALIA P A,DELMAS J P,ABEDMERAIM K.A blind multichannel identif ication algorithm robust to order estimation[J].IEEE Transactions on Signal Processing.2002,50(6):1449-1458.

[9]ZENGY H,NGT S.Blind estimation of MIMO channels with an upper bound for channel orders[J].Signal Processing,2006,86(2):212-222.

[10]ZENGY H,NGT S.A semi-blind channel estimation method for multiuser multiantenna OFDM systems[J].IEEE Transaction on Signal Processing,2004,52(5):1419-1429.

[11]GAO F,ZENG Y H,NALLANATHANA,TUNG-SANG N.Robust subspace blind channel estimation for cyclic pref ixed MIMO OFDM systems:algorithm,identif iability and performance analysis[J].IEEE Journal on Selected Areas in Communications.2008,26(2):378-387.

[12]HAO Lihong,LI Guangjun,GUO Zhiyong.Nonredundant precoding blind channel estimation for MIMO-OFDM systems[C]//IEEE International Conference on Computer Engineering and Technology,2010:V1-319-V1-322.

[13]SONGWang,CAOJinli,HUJiankun.A frequency domain subspace blind channel estimation method for trailing zero OFDM systems[J].Journal of Network and Computer application,2011,34(1):116-120.

[14]XINXiong,BINJiang,GAOXiqi,YOUXiaohu.DFTbased channel estimator for OFDM systems with leakage estimation[J].IEEE Communications Letters,2013,17(8):1592-1595.

[15]LIF,LIUH,VACCAROR J.Performance analysis for DOA estimation algorithms:further unif ication,simplif ication,and observations[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(4):1170-1184.

[16]DE CARVALHO E,CIOFFI J,SLOCK D.Cramer-Rao bounds for blind multichannel estimation[C]//IEEE Global Telecommunications Conference,2000:1036-1044.