基于移动最小二乘与控制曲线的3D点云变形

王 瑞， 肖 任， 陈俊丽， 余宗鑫， 万旺根

1.上海大学通信与信息工程学院，上海200444

2.上海大学智慧城市研究院，上海200444

三维扫描技术的发展，使得获取具有丰富几何细节的数字模型成为现实.用点云来表示具有复杂表面几何的三维物体与传统的三角面片表示方法相比，具有存储简单、无需维护拓扑结构以及显示高效等优点.随着大规模采样点模型在图形学和几何信息处理中的广泛应用，3D点云的变形方法在几何建模、3D动画生成、动态场景绘制及动态模拟等方面有着独特的优势及广泛的应用价值，是点云研究领域的一个热点[1].

目前，关于三维物体变形的算法主要有自由变形法[2]、基于广义球元(metaball)的约束变形[3]、多分辨率下的网格技术变形[4]、基于泊松梯度场的几何变形技术[5]等.与上述方法相比，移动最小二乘法在变形结果上呈现出更精确、更能保留原始信息等优势，尤其是三维刚性变换[6].文献[7]将2D移动最小二乘法有效地延伸到3D上，通过设置控制点实现了大量网格顶点的3D变形.文献[8]基于权重定义了新的测地线度量，并根据移动最小二乘法在使用平滑与完整的数据基础上实现了较好的3D变形.文献[9]基于3D移动最小二乘法提出了纹理引导下的体变形与可视化方法.

在控制点不足等诸多因素的影响下，基于移动最小二乘法的变形不流畅，甚至发生畸变，可能无法得到理想的效果.为此，本文提出了基于控制曲线的3D点云变形方法，用空间曲线表示3D点云模型的形状拓扑关系或轮廓信息，可方便操作控制曲线变化，得到更精确且更真实的变形效果.

1 基于控制点的3D点云变形

将3D点云变形看成在变形函数f作用下由未变形点云映射到变形点云的过程，将f作用于未变形点云顶点，可以得到变形后的3D点云模型[8].设pi表示变形前的控制点(xi,yi,zi)，qi表示变形后控制点的(¯xi,¯yi,¯zi).根据移动最小二乘理论模型[10]对点云数据进行三维变形，对于空间中的任一点v，需要求出变形函数f(x)，使式(1)取最小值

式中，pi和qi为控制点坐标向量，wi为权重，其计算公式为，α为调节变形效果的参数.

权重wi的取值随着顶点v在3D点云中取点位置的不同而变化.当v取值为控制点si时，wi将趋向无穷大，此时定义T(pi)=qi；若控制点坐标值不变，则定义f(si)=si.一般地，将变形函数设为f(v)=M x+T，其中M表示线性变换项，T表示平移变换项.在式(1)取最小值的情况下可求得

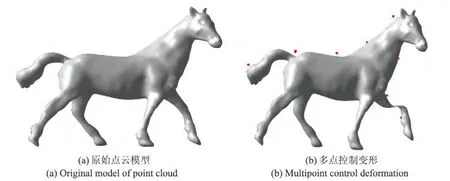
图1 基于控制点的3D移动最小二乘变形Figur e 1 3D least-squares deformation of horse leg based on control points

将T代入变形函数可得

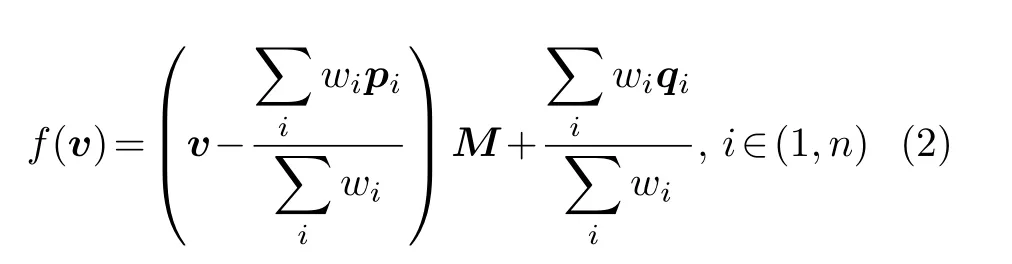
令

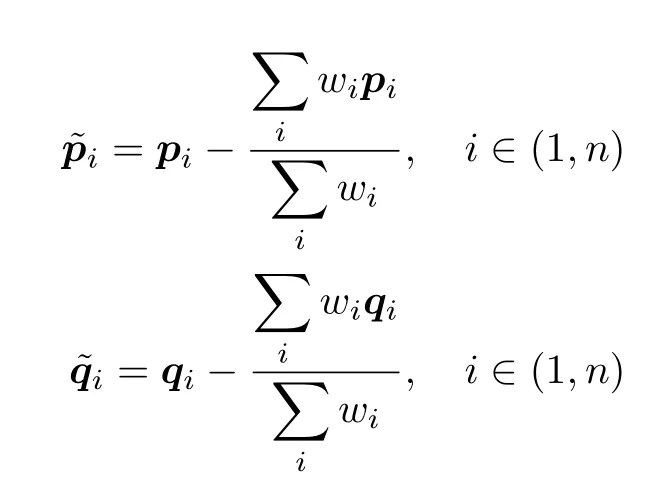
则式(1)等效于

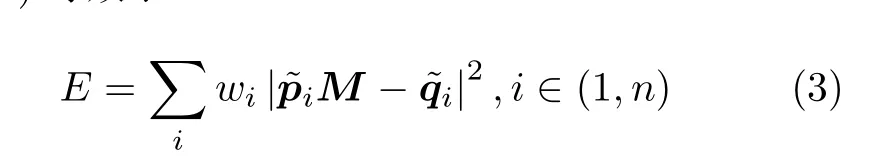
从而得到了基于控制点集的3D点云移动最小二乘法变形.矩阵M可视为仿射变换，包含了缩放、错切、旋转等变换成分.通过对这些成分进行组合分析，可以获得仿射变换、相似变换以及刚性变换的变形函数f(v).

对于马的3D点云模型，如果只有一个控制点，就会使整个点云模型产生平移，不能充分展现马蹄提起的变形效果.本文主要研究点云模型的刚性变形，设置多个控制点(包括固定控制点和移动控制点)进行变形.通过移动多个控制点对点云模型变形，实现马蹄抬起效果，如图1所示.基于控制点的3D点云刚性变换变形后的效果如图1中的(b)所示，可以看到马蹄发生畸形，点云模型的真实感较差.针对基于控制点变形时表现出的弊端，本文将讨论基于控制曲线集的变形.

2 基于控制曲线的3D点云变形

针对控制点变形的不足，本文提出一种基于控制曲线的3D点云变形算法，用曲线描述3D点云数据的形状和轮廓信息，获得了更精确的变形效果.为较好地控制曲线路径，本文使用三次样条曲线拟合方法生成控制曲线，即对控制点采用分段拟合，使拟合结果更加精确.

2.1 三次样条曲线拟合

为了拟合点云数据空间的一条曲线，首先将待求的曲线投影到两个平面，然后分别对这两个平面进行三次样条插值拟合，最后将拟合好的二维曲线组合成三维曲线.下面给出理论分析.

在三维空间中，曲线有两个方向的斜率，一个是关于x轴方向的斜率，另一个则是关于y轴方向的斜率.故设曲线表达式为

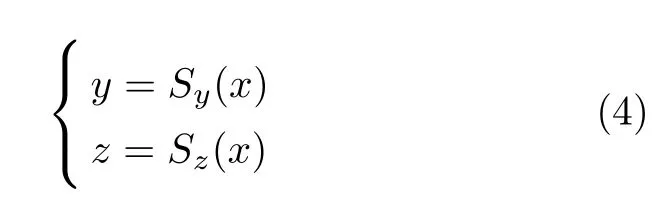
式(4)分别为该曲线在xoy和xoz平面上的投影.令Sy(x)=S(x)，设x1＜x2＜x3＜···＜xn-1＜xn共n插值节点，则经过数据点(x1,y1),(x2,y2),···,(xn,yn)的三次样条S(x)是一级三次多项式

由节点处的连续性可知

由节点处的一阶与二阶光滑性可知

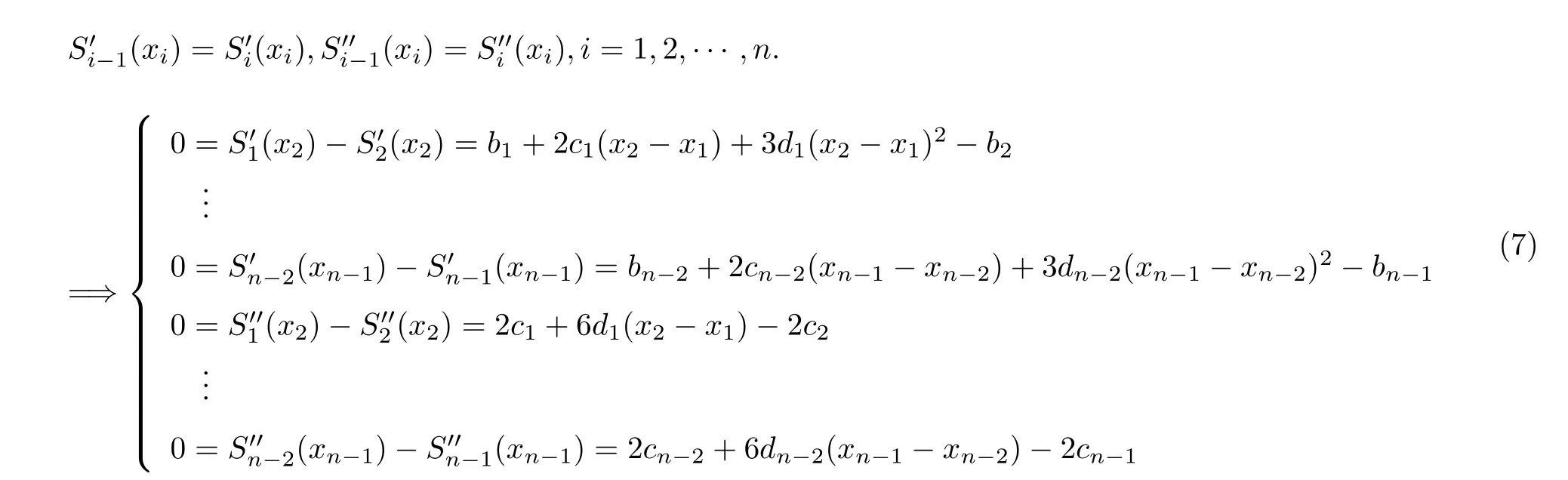
由式(6)可得

将式(8)和(9)代入式(7)，可得

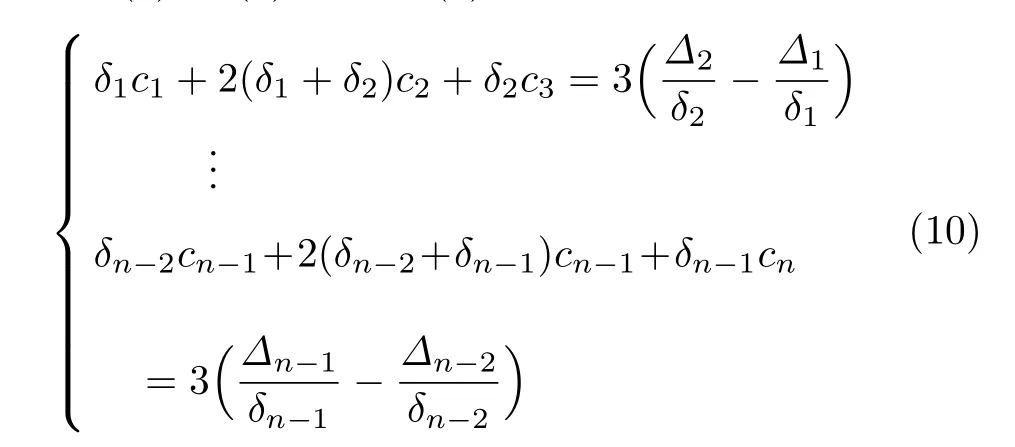
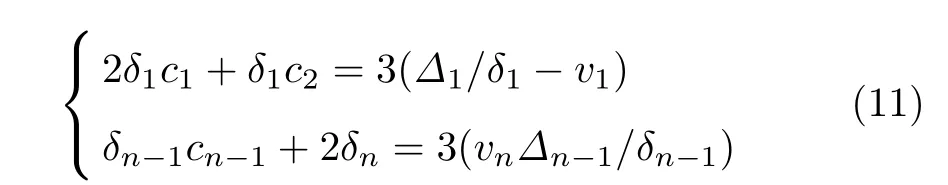
结合式(10)以及所给的边界条件即可解出{ci}.联立式(4)～(6)、(8)、(9)、(11)可得

根据式(12)可以得到由p点拟合的曲线lp(xp,yp(xp),zp(xp))，进一步可知曲线上的点满足p(x)=(x,yp(x),zp(x)).

同理可得lp(xp,yp(xp),zp(xp))和q(x)=(x,yq(x),zq(x))，易知式(2)所得到的变形函数是通过几个离散点计算得来的，所得函数的准确度受控制点数目的限制.现已获得拟合好的控制曲线lp和lq，可对其进行推广

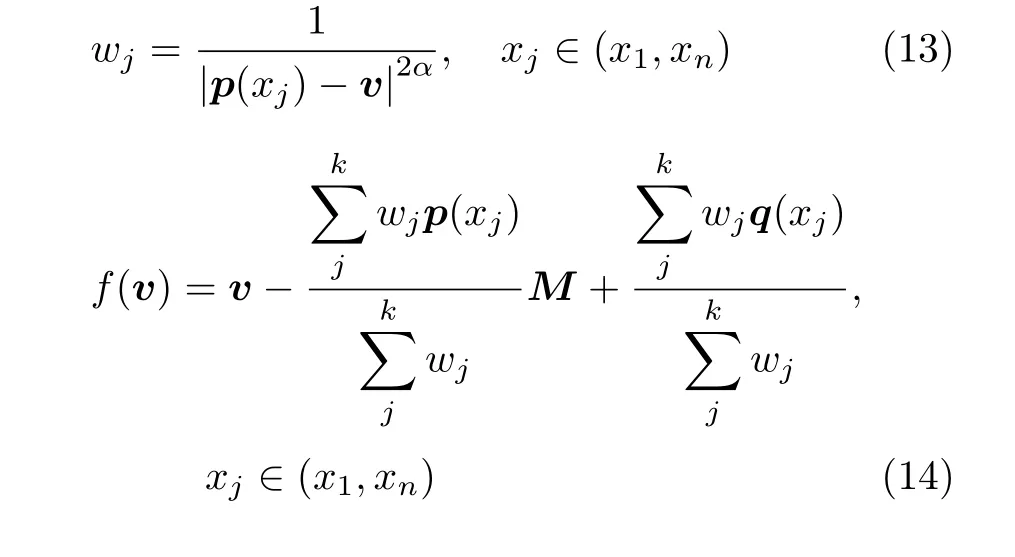
式(1)可推广为

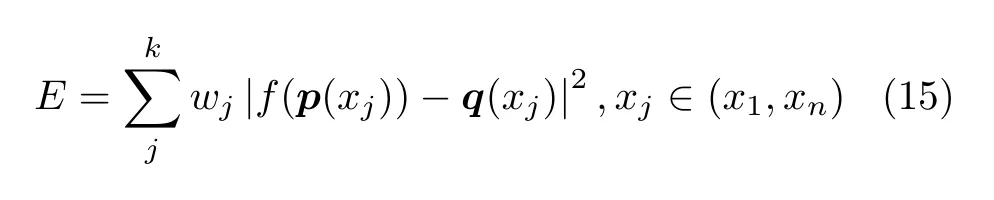
式中，xj可取(x1,xn)中的任何数，所取点数不受限制;k为拟合时所需要的所有点数，k值越大控制点的数目就越多，拟合效果越平滑.

2.2 基于控制曲线的3D点云变形

使用三次样条曲线拟合方法对控制点集进行分段拟合，生成控制曲线lp.拟合的曲线lq可精确地通过控制点实现变形，其具体步骤如下：

步骤1 设置关键点，通过三次样条插值拟合成曲线集Lp.

步骤2 移动Lp上的点，改变样条曲线的位置和方向生成曲线集Lq.

步骤3 更改起点斜率u1和末端斜率un，改变Lp和Lq的边界条件和线上的插值点数，拟合模型的表面轮廓和目标形状.

步骤4 根据曲线上Lp和Lq两条曲线计算变形后的模型.

3 实验分析

根据本文提出的算法以及推导的变形公式对3D点云模型进行控制点和控制曲线的变形实验.实验所用微机配置如下：Intel i3处理器、内存4 GB、显卡GeForce 9300 GS.为改善图1中基于控制点的马腿变形效果，利用三次样条拟合的方式生成控制曲线，以实现3D点云模型的变形.控制曲线拟合后选取5个、10个、40个插值点的变形效果如图2所示，其中红线为曲线拟合的轨迹.通过改变曲线两端的斜率可以改变拟合曲线的弯曲度，获得满意的变形效果.

为了对比不同情况下的变形效果，分别对马的模型进行仿射变换和刚性变换，结果表明刚性变换下具备更好的变形效果.此外，图3还对马模型进行了基于控制曲线集的移动最小二乘的变形，使得马尾巴和马腿同时变形，表明了拟合效果较理想.

如果变形效果还不够理想，可以通过改变曲线端点处的一阶导数来实现调节，故在下面实验中令u1=

图4所示的实验结果表明，通过调节u1和un可以使曲线拟合出较好的变形效果.

图2 基于控制曲线的3D移动最小二乘变形Figure 2 3D move least-squares deformation based on control curve

图3 基于控制曲线集的同时变形(马尾和马腿)Figur e 3 Simultaneous deformation based on the control curves(horsetail and horse leg)

图4 改变曲线两端的一阶导数后的变形效果Figure 4 Effect of deformation after change first derivative of the ends the curve

4 结语

以曲线的方式拟合3D点云模型的轮廓信息，同时结合移动最小二乘方法提出了一种新的3D点云变形算法.根据点云数据的形状信息或变形需要，使用三次样条插值拟合关键点的方式生成控制曲线，结合移动最小二乘法实现3D点云模型的刚性变形，通过轮廓拟合准确定位变形后的物体轮廓，利用控制曲线可实现多个点云区域的准确变形.实验分析验证了该方法的合理性与有效性.下一步工作将研究大规模点云数据的变形及交互技术.

[1]谭光华，许秋儿，吴双卿，张三元，张引.特征保持的大规模点云曲面自由变形[J].浙江大学学报：工学版，2010,44(1):34-40.TAN Guanghua,XU Qiuer,WU Shuangqing,ZHANG Sanyuan,ZHANG Yin.Features preserved massive point cloud surfaces freeform[J].Journal of Zhejiang University:Engineering Science,2010,44(1):34-40.(in Chinese)

[2]SEDERBERG T W,PARRY S R.Free-form deformation of solid geometric models[C]//Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques.New York:ACM Press,1986,20(4):151-160.

[3]金小刚，彭群生.基于广义元球的一般约束变形[J].软件学报，1998,9(9):677-682.

JIN Xiaogang,PENG Qunsheng.Generalized constraints deformed based on the general dollar ball[J].Journal of Software,1998,9(9):677-682.(in Chinese)

[4]KOBBELT L,CAMPAGNA S,VORSATZ J,SEIDEL H.Interactive multi-resolution modeling on arbitrary meshes[C]//Proceedings of SIGGRAPH,Orlando,Florida,1998:105-114.

[5]YUY,ZHOUK,XUD,SHIX,BAOH,GUOB,SHUM H.Mesh editing with Poisson-based gradient field manipulation[J].ACM Transactions on Graphics,2004,23(3):644-651.

[6]ALEXA M,COHENOR D,LEVIN D.As-rigid-aspossible shape interpolation[C]//SIGGRAPH Conference on Computer Graphics and Interactive Techniques,2000:157-164.

[7]CUNO A,ESPERANCA C,OLIVEIRA A,CAVALVANTI R.3D As-rigid-as-possible deformation using MLS[C]//Computer Graphics International Conference,2007:1-8.

[8]ZHU Y,GORLER S J.3D deformation using moving least squares[R].Harvard Computer Science Technical report:TR-10-07,Cambridge,2007:1-5.

[9]ZHAO X,LI B,WANG L,KAUFMAN A.Textureguided volumetric deformation and visualization using 3D moving least square[J].IET Compute Vision,2012,28:193-204.DOI 10.1007/s00371-011-0635-2.

[10]SCHAEFER S,MCPHAIL T,WARREN J.Image deformation using moving least squares[J].ACM Transactions on Graphics,2006,25(3):533-540.