运用压缩感知理论的图像稀疏表示与重建
丰 祥, 万旺根
1.上海大学通信与信息工程学院,上海200444
2.上海大学智慧城市研究院,上海200444
信号处理的依据是奈奎斯特采样定理,即如果要精确地重构原始信号,必须使用大于信号最高频率两倍的频率进行信号采样,这就导致信号采样过程中产生大量冗余数据,而最终只有部分重要的信息被应用.文献[1]在可压缩信号的稀疏分解与信号恢复基础上提出了压缩感知理论框架,随后该理论迅速发展,为解决瓶颈问题提供了理论基础.在此基础上,Candes等人正式提出了压缩感知这一术语.此后,人们在稀疏表示的稀疏性[2]与不相干性、压缩采样的稳健性、感知测量等[3]方面开展了许多研究工作,并将压缩感知作为测量技术应用于天文学、核磁共振、模式识别等领域,取得了较好的研究成果[4].
压缩感知理论是对经典信号处理领域的补充和完善,引起了众多学者和组织机构的关注,其应用领域包含图像处理与重建、数据融合和医学信号检测等.文献[5]研究了压缩感知稀疏表示算法;文献[6-7]详细探讨了压缩感知理论中约束等距性(restricted isometry property,RIP)矩阵的构造问题;文献[8]研究了压缩感知理论在探地雷达三维成像中的应用;文献[9]探索了感知测量矩阵在实际应用中的设计问题;文献[10-11]将压缩感知理论用于解决医学图像重建和图像去噪等问题.
文献[12]提出了基于多观测向量和稀疏贝叶斯学习的重建算法,并将压缩感知理论用于图像重建,但没有考虑图像分块和稀疏表示方法对图像重建的影响.文献[13]基于多种稀疏变换基和观测矩阵研究图像重建,但没有考虑图像分块和采样率对图像稀疏重建的影响.本文分析比较了离散余弦变换和离散小波变换两种稀疏表示算法,通过调节分块大小和采样率大小对标准测试图像进行重建实验,并在运行时间、重构误差和视觉效果方面综合比较两种算法对稀疏重构效果和效率的影响,指出了各自算法的优缺点,分析了分块大小和采样率大小对图像重建效果的影响.
1 压缩感知的研究内容
压缩感知理论采用低于奈奎斯特采样定理要求的频率采样、编码和重构,适用于更广泛的信号类型.该理论主要涉及稀疏变换、观测测量和恢复重建3个基本核心问题[14],其流程图见图1.压缩感知要求原始信号为可压缩信号,即首先可以通过稀疏变换把原始信号转化为稀疏信号,然后使用观测矩阵对稀疏变换进行观测测量,得到低维的观测信号,经传输和存储等过程后,根据恢复重建算法将观测信号重构出原始信号.
稀疏变换是在假设自然信号可以被压缩表示时对多维数据进行线性分解的一种表示方法,它具有过完备性和稀疏性两个基本特征.过完备性表示字典的行数大于列数,稀疏性表示信号非零元数目足够少.本文针对离散余弦变换和离散小波变换这两种稀疏变换进行研究.观测测量指的是:对信号的线性投影采用一个与稀疏变换矩阵不相关的测量矩阵得到感知测量值,以确保精确地重构原始信号.测量矩阵应满足非相干性和限制等容性两个基本原则.常用的随机性测量矩阵包括随机高斯测量矩阵、随机伯努利矩阵、部分正交矩阵、稀疏随机矩阵等,本文则采用正交归一化的随机高斯矩阵进行观测测量.信号重构算法是指用压缩测量的低维数据精确地重构高维的原始信号或图像,即利用M维测量值重建N维信号(M远小于N)的过程.信号重构是压缩感知研究中最重要而关键的部分.目前主流的重构算法分为3类:基于最小l范数的凸优化算法、贪婪算法、非凸优化算法,其中贪婪算法在保证重建精度的同时具有较快的重建速度,于是本文采用贪婪算法中的正交匹配追踪算法进行恢复重建.
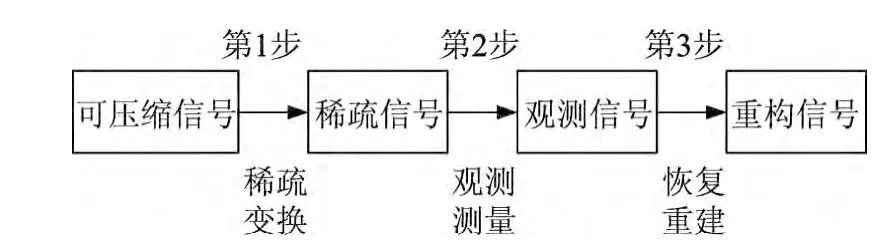
图1 压缩感知理论流程图Figure 1 Flowchart of compressed sensing theory
2 图像的稀疏表示与恢复重建
为了对图像信号进行稀疏表示,应先把信号变换到稀疏域.本文在图像稀疏表示阶段采用离散余弦变换和离散傅里叶变换进行对比性研究,在图像恢复重建阶段采用正交匹配追踪算法进行重建.
2.1 图像的稀疏表示
2.1.1 离散小波变换
若ψ(t)∈ L2(R),(L2(R)为ψ(t)的矢量 空间,R为实数集),a0>1为扩张步长,ψj,k(t)=则定义一维信号x(t)的离散小波变换(DWT变换)为
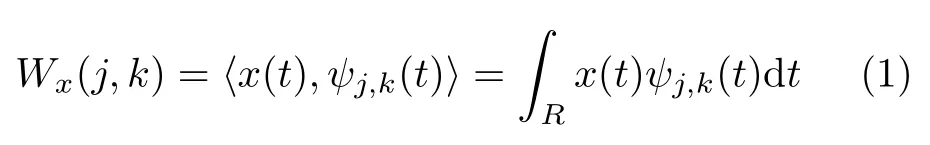
当a0=2且τ0=1时,所有的采样点所形成的图形被称为二进网格,此类离散小波变换被称为二进小波变换.它只选择部分缩放因子和平移参数进行离散小波变换,大大减少了分析的数据量.
假设一幅图像大小为N×N,该图像可以用长度为N的二维方阵X进行表示,w w表示长度为N的一维离散小波变换所对应的正交规范化变换矩阵,则矩阵X的二维离散小波变换为
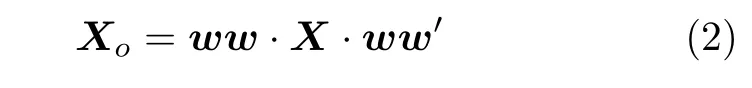
该变换可以分解为以下两步来执行:1)对矩阵X的每一行数据序列进行一维离散小波变换Xi=X·w w′;2)对变换后矩阵Xi的每一列进行离散一维小波小波Xo=ww·Xi.Xo往往是稀疏的,它属于稀疏矩阵;X属于可压缩信号.在实际过程中,为了提高稀疏重构效率,通常将整体图像分成若干个大小为Nb×Nb的小块进行处理,每一分块在水平方向和垂直方向的索引号分别为x和y,对应的正交小波变换为=w w·Xx,y·w w′.记M为测量数据量大小,η=M/N0.测量矩阵取为行正交规范化的随机高斯矩阵R,各个分块的测量值为Y=R·Xx,yo,采用正交匹配追踪法求得重构值^Xx,yo,经过小波逆变换计算出图像域的数据值=ww··w w′,最后根据分块的顺序合成整体图像并进行显示.
图像经过DWT变换后得到低频部分系数和高频部分系数,低频部分系数通常具有非稀疏性,而高频部分系数具有良好的稀疏性.如果低频部分系数与高频部分系数都作为原始信号进行感知测量,往往会导致重构图像质量严重下降[15].尺度越小分辨率越高,则高频成分越多,小波分解的尺度对重构结果具有重要的影响.
2.1.2 离散余弦变换
离散余弦变换将数据线性地变换到频域,并用一系列系数来表示数据,其优点是可以把原始数据的能量集中在少数低频成分,因为原始数据的相关性越强,能量越集中.离散余弦变换(discrete Cosine transform,DCT)常用于图像数据的压缩,经过DCT变换后的数据能量非常集中,主要集中于离散余弦变换后的直流部分和低频部分.
对于N×N的二维图像信号f(x,y),0≤x,y≤N-1,其二维离散余弦变换的正变换公式为
2018年9月10日习总书记在全国教育大会上强调:“教师是人类灵魂的工程师,是人类文明的传承者,承载着传播知识、传播思想、传播真理,塑造灵魂、塑造生命、塑造新人的时代重任”。由此可见,高校辅导员肩负着立德树人的神圣使命,只有谨记教育之初心,率先垂范,为人师表,立德、立言、立行,不断提高自身学识修养,才能做好学生健康成长的人生导师。笔者认为,高校辅导员具体可以从如下四个方面着手努力:
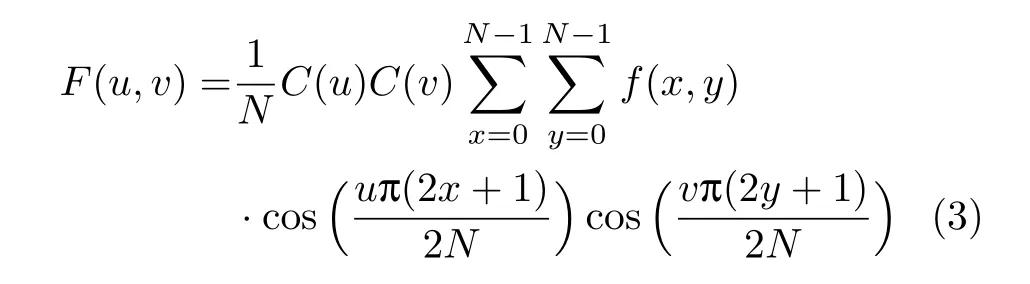
相应的二维DCT变换的反变换公式为
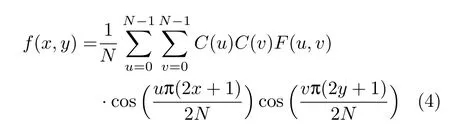
式(3)和(4)中的系数为
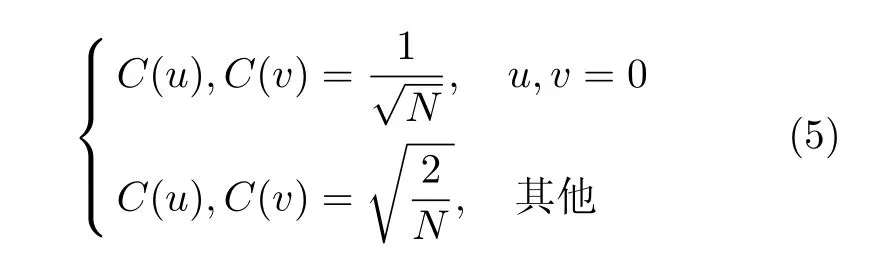
2.2 信号的恢复重建
正交匹配追踪(orthogonal matching pursuit,OMP)重构算法的原理如下[16]:以贪婪迭代的方法选择恢复矩阵R的列,使得每次迭代中所选择的列与当前的残差向量最大程度地相关,再从测量向量中减去相关部分,反复迭代直到迭代次数达到稀疏度K时停止迭代.该算法的输入参数为恢复矩阵R、测量向量y、稀疏度K,输出参数为原始信号x的K稀疏逼近^x.算法的主要步骤如下:
步骤1 初始化残差r0=y,索引集Λ0=∅,迭代次数t=1,循环执行步骤2~5.
步骤2 找出残差r和感知矩阵的列φj积中最大值所对应的角标λt,即λt=argmaxj=1,···,N|〈rt-1,φj〉|,记录最大值所对应的列向量.
步骤3 更新索引集Λt=Λt-1∪{λt},记录找到的感知矩阵中的重构原子集合Φt=[Φt-1,φλt].
步骤5 判断迭代次数是否满足t>K,若满足,则停止迭代并跳转到步骤6;若不满足,则执行步骤2.
步骤6 将最终的^x值作为稀疏重构向量.
3 实验仿真与分析
3.1 实验说明
本文采用大小为N×N(N=512)的灰度图像Lena、Cameraman和Peppers作为标准测试图像,图像分块时的分块边长Nb取值为32、64、128,采样率η取值为0.3、0.4、0.5.本文将比较DCT变换和DWT变换在图像稀疏表示时的性能,采用正交归一化的随机高斯测量矩阵进行感知测量,根据正交匹配追踪算法进行图像信号的恢复重建,以时间消耗t和重建误差σ表征不同分块大小Nb和采样率η条件下的重建效率和性能.其中,时间消耗包含信号分解、感知测量和信号重建整个过程中所花的时间.令Xerror为整体重建图像与整体原始图像X之间各个像素差值的平方和,则重建误差为
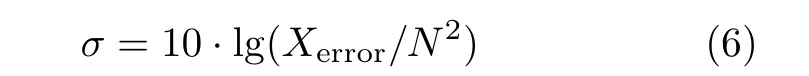
所有实验均在MATLAB R2011b环境下完成,计算机的CPU性能参数为i5-2400 3.10 GHz,内存大小为2.00 GB.
3.2 实验仿真比较与数据分析
当改变采样率和分块大小时,记录时间消耗和重建误差,采用DCT变换和DWT变换得到的实验数据如表1和2所示.由表1和2可以发现,无论是采用DCT变换还是采用DWT变换,都满足以下结论:在分块大小固定的条件下,时间消耗随着采样率的提高而增加,而重建误差随着采样率的提高而降低;在采样率固定的条件下,运行时间随着分块大小的增加而增加,而重建误差随着分块大小的增加而降低.本文以Lena图像和DCT变换为例,在不同采样率和分块大小时分别比较重建误差和时间消耗,结果如图2所示.在实际应用中,往往难以同时获得最短的时间消耗和最小的重建误差,这就需要根据实际需求合理地选择分块大小和采样率,以实现最佳的重建效果.
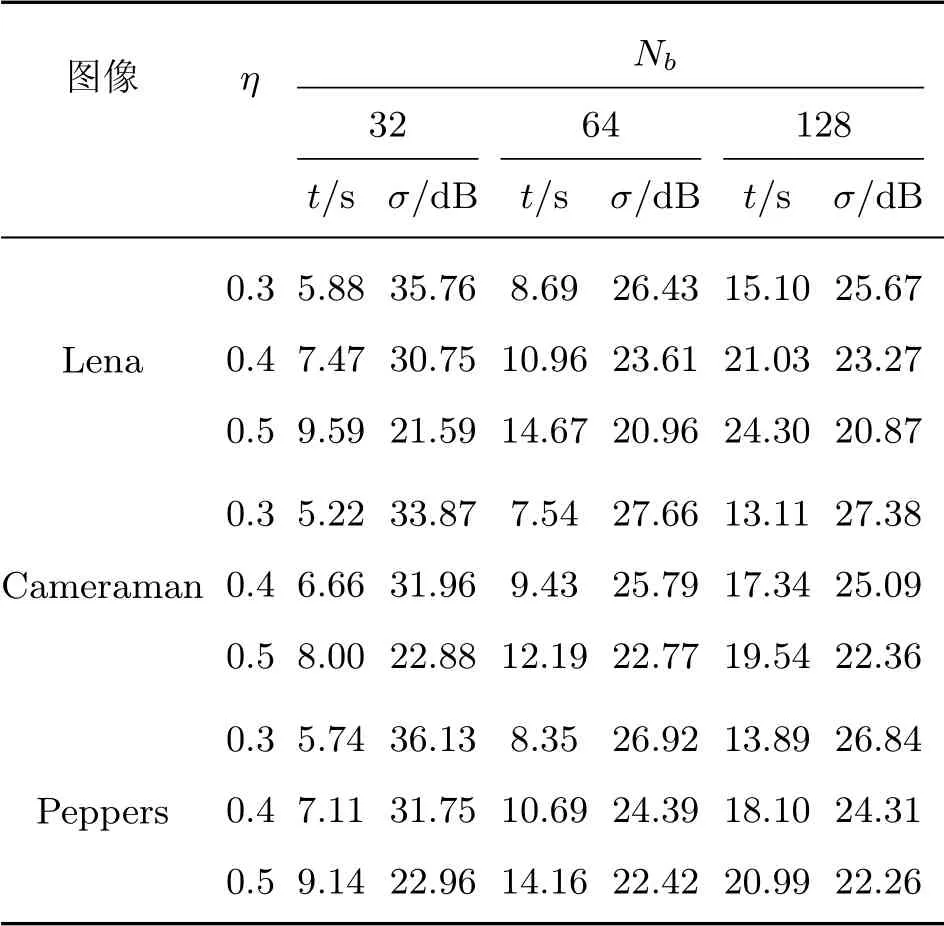
表1 采用DCT变换时的重建性能Table 1 Reconstruction performance using DCT transform
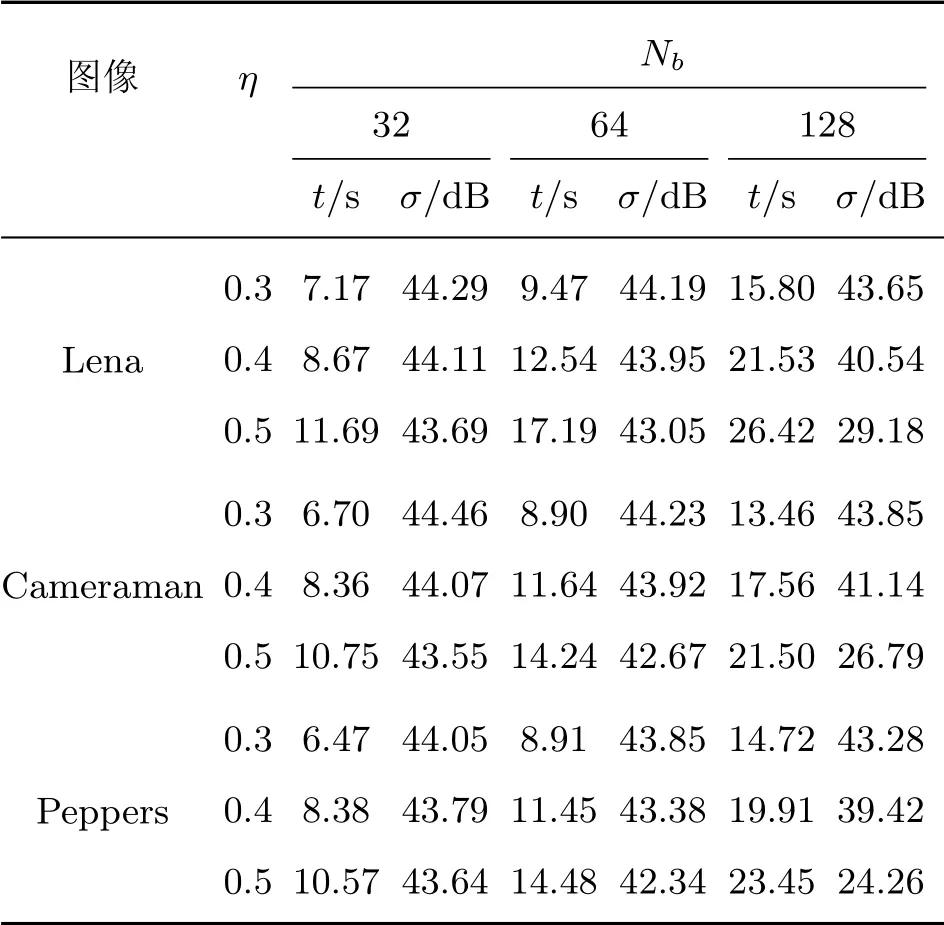
表2 采用DWT变换时的重建性能Table 2 Reconstruction performance using DWT transform
对比表1和2的重建误差和时间消耗数据容易发现:在相同的分块大小和采样率条件下,对相同的标准图像进行测试,采用DCT变换时重建误差和时间消耗都比采用DWT变换时小,采用CT稀疏表示在图像重建方面往往表现出更优的性能.图3为原始标准的测试图像,图4表示在Nb=128,η=0.5时分别采用DCT变换和DWT变换时所对应的测试图像重建效果图.对比图3和4可以发现,采用DWT变换时的重建图像往往大部分区域较清晰,而在小部分区域会出现明显的局部带状条纹;采用DCT变换重建图像的整体清晰度比采用DCT变换时重建图像的整体清晰度较差,但不会出现明显的带状条纹.
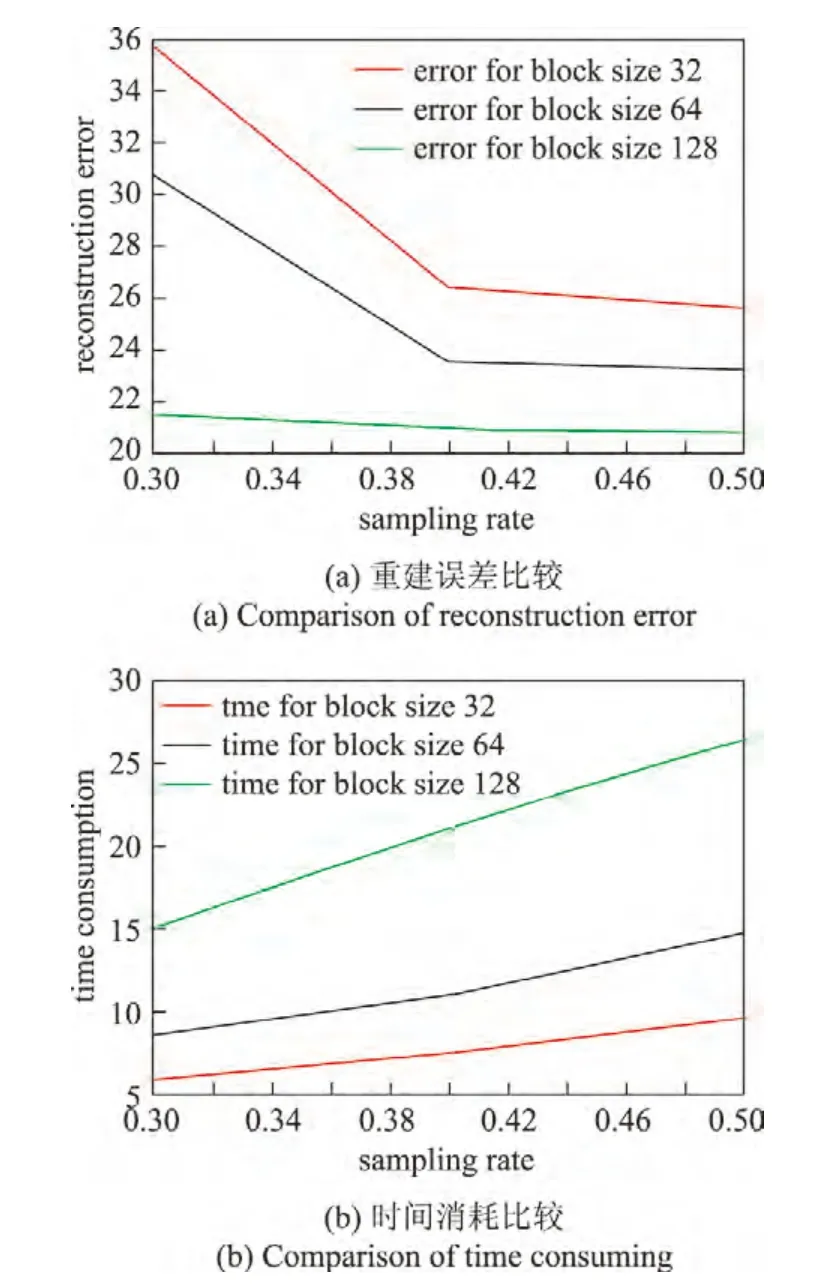
图2 以Lena图像和DCT变换为例,重建误差和时间消耗比较图Figure 2 Comparison of reconstruction error and time consuming with Lena image and DCT for example
分析表1、表2、图3、图4可知,采样率的适当选取与测量信号的稀疏程度密切相关,而对于非稀疏信号,较低的采样率则会严重影响重建图像的质量.相比于DWT变换,DCT变换因不受小波分解尺度的影响而在图像的稀疏化表达方面表现得更加稳定.本文采用sym8作为小波基,保持小波分解尺度不变,并且可以调整分块大小,此时分块大小越小,重构图像质量则越差.在采样率为0.5、分块大小为128的情况下,小波分解尺度对稀疏度的影响相对较小,采用DWT变换时的重建误差与采用DCT时的重建误差相比差异也较小;而当分块大小减小或采样率下降时,采用DWT变换时的重建效果则明显降低.

图3 原始标准测试图像Figure 3 Original standard test images

图4 分别为使用DCT变换和DWT变换时的稀疏重建图像Figure 4 Reconstructed images using DCT transform and DWT transform respectively
4 结论
本文将压缩感知理论应用于图像的稀疏重建,在图像的感知测量和恢复重建过程中分别采用了正交归一化的随机高斯矩阵和正交匹配追踪算法,在图像的稀疏表示过程中采用DCT变换和DWT变换,并在不同的分块大小和采样率条件下,根据时间消耗和重建误差两个性能参数对各自的性能进行了综合比较.在分块大小固定的条件下,时间消耗随着采样率的提高而增加,而重建误差随着采样率的提高而降低;在采样率固定的条件下,运行时间随着分块大小的增加而增加,而重建误差随着分块大小的增加而降低,在图像的稀疏表示与重建方面,DCT变换整体上比DWT变换表现出相对更优的性能.在实际应用中需根据对重建图像的要求,结合分块大小和采样率等关键因素对重建性能的影响,合理地选择分块大小和采样率,以实现整体最优的重建效果.下一步我们将针对不同的图像进行自适应分块,希望在时间消耗和重建质量等方面取得更好的效果.
[1]CANDES E J,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[2]LIU J,MALLICK M,HAN C Z,YAO X H,LIAN F.Similar sensing matrix pursuit:an efficient reconstruction algorithm to cope with deterministic sensing matrix[J].Signal Processing,2014,95:101-110.
[3]LIU Xiaoman,ZHU Yonggui.A fast method for TVL1-MRI image reconstruction in compressive sensing[J].Journal of Computational Information Systems,2014,10(2):691-699.
[4]MICCHELLI C A,SHEN L X,XU Y S,ZENG X Y.Proximity algorithms for the L1/TV image denoising model[J].Advances in Computational Mathematics,2013,38(2):401-426.
[5]XU Zhiqiang.Deterministic sampling of sparse trigonometric polynomials[J].Journal of Complexity,2011,27(2):133-140.
[6]BOURGAIN J,DILw ORTH S J,FORD K,KONYAGIN S,KUTZAROVAD.Explicit constructions of RIP matrices and related problems[J].Duke Mathematical Journal,2011,159(1):145-185.
[7]ZHANG Tong.Sparse recovery with orthogonal matching pursuit under RIP[J].IEEE Transactions on Information Theory,2011,57(9):6215-6221.
[8]YU Huimin,FANG Guangyou.The application of compressive sensing in the three dimensional imaging of ground penetrating radar[J].Journal of Electronics and Information Technology,2010,32(1):12-16.
[9]FU Qiang,LI Qiong.The research of constructing the measurement matrix in compressive sensing[J].Computer and Telecommunication,2011,7(1):39-41.
[10]WANG Yan,LIAN Qiusheng,LI Kai.MRI image reconstruction based on joint regularization and compressed sensing[J].Optical Technology,2010,36(3):350-355.
[11]QU Xiaobo,GUO Di,NING Bende.Undersampled MRI reconstruction with the patch-based directional wavelets[J].Magnetic Resonance Imaging,2012,30(7):964-977.
[12]LI Zhilin,CHEN Houjin,LI Jupeng,YAO Chang,YANG Na.An efficient algorithm for compressed sensing image reconstruction[J].Acta Electronica Sinica,2011,39(12):2796-2800.
[13]HOU Jinman,HE Ning,LÜKe.Image fast reconstruction method based on compressive sensing[J].Computer Engineering,2011,37(19),215-217.
[14]YINHongpeng,LIUZhaodong,CHAIYi,JIAOXuguo.Survey of compressed sensing[J].Control and Decision,2013,28(10):1441-1445.
[15]YUAN Quan,ZHANG Cheng,CHEN Jianjun,YAO Junxia,LIYingran,WANGHuan.Image compressed sensing based on wavelet transform[J].Computer Engineering,2012,38(20):209-218.
[16]CARMIA Y,MIHAYLOVAL S,GODSILLSJ.Introduction to compressed sensing and sparse f iltering[M].Berlin Heidelberg:Springer,2014:1-23.

