一种基于信息容量的模体比较非比对度量算法
郭丽娟,张少强,花季伟
(天津师范大学计算机与信息工程学院,天津300387)
破译基因组中复杂的基因调控网络是一项极具挑战性的课题[1-2],要实现这个目标,首先要在基因组中鉴别所有转录因子的结合位点[1,3-4].转录因子结合位点是转录因子结合的一组短基因序列,长度通常为6~25个碱基对(base pair,bp),具有触发细胞转录调控的功能.属于同一转录因子的结合位点通常具有特定的保守性和相同的长度,但它们也可以显示出一定程度的变异,而这些结合位点位于一段非常长的非编码序列中,这些都会导致它们的预测计算变得非常困难.同一转录因子的一组具有高保守性的结合位点通常被称作模体,可以由实验验证,或者通过比较一组可能含有转录因子结合位点的方法预测.由于转录因子结合位点比它们周围的DNA片段更保守,所以,许多从头测序模体查找算法被开发出来用于识别转录因子结合位点.模体可以由位置赋权矩阵(position weight matrix,PWM) 和位置频率矩阵(position frequency matrix,PFM)精确地表述出来[5-6].这2个矩阵是模体结合位点序列比对的变形,它们极大程度上反映了相应的转录因子的位置结合倾向性.因此,通过在这2个矩阵中扫描可能包含TFBS的序列即可以发现模体.
利用模体查找工具获得一些假定的模体后,通过在一个模体数据库中找到与假定模体匹配的模体,从而推断出转录因子附属于这些假定的模体[7];或聚类相同转录因子的相似子模体从而去除冗余模体、形成一个完整的模体.因此,在上述提到的应用中,需要一种有效的度量法用于捕获不相关模体之间的细微差别,强调同种群间模体的相似度.目前,计算模体相似度的比对度量方法包括两大类:一类是列相似度度量法,即从2个模体的位置频率矩阵(或者位置赋权矩阵)中各取一列计算相似性,如SSD(sum of squared distances)[8-9]、pCS (p-value of Chi-square)[10]、ALLR (average log-likelihood ratio)[11]、AKL(average Kullback-Leibler,AKL)[12]和 PCC(pearson’scorrelation coefficient,PCC)[13]等;另一类是双序列比对算法,利用列相似度度量法和一个空位罚分函数作为分数比对2个模体[14],在假定具有空位罚分函数的情况下,Needleman-Wunsch 算法[15]和 Smith-Waterman(SW)算法[16]都可用于查找最优比对.文献[7]和文献[17]对这些度量和比对算法进行评估后,建立了网络服务器STAMP,用于集成这些带有比对的度量法.除此之外,还有2个用于比较模体的非比对度量方法KFV(kmer frequency vector) 和 Mosta 包 的 AC(Asymptotic Covariance),它们分别由文献[7]和文献[15]提出.
上述度量方法仅用到了位置频率矩阵,均没有使用列信息容量(column information contents)和位置赋权矩阵.实际上,由于矩阵中所对应的列具有很高的相关性,2个总体信息容量低的模体也可能具有高的相似度分数.因此,如果2个模体某些列的信息容量很低,在应用这些度量方法比对前,低信息容量的列就要被删除.上述带有比对的度量方法在聚类相似模体方面具有较好的效果,但是它们基本不能从带有低信息容量列的混杂模体中分离出真模体.此外,带有比对的度量公式需要用到比对算法,而比对算法依赖的参数较多,运行所需时间也较多,因此基于非比对的度量公式可以更快速精确地进行模体比较.综上所述,本研究提出一种带有位置信息容量的相似度非比对度量法(information contents based similarity metric,ICBSM).算法中不仅包含位置频率矩阵和位置赋权矩阵,还加入了每个位置的信息内容,并利用来自于 STAMP[17]、KFV[14]和 GLECLUBS[18-19]中的数据集对ICBSM算法进行评估,将该算法与国际上已经提出的算法进行比较分析.
1 ICBSM方法
1.1 ICBSM度量法的提出
设模体Motif由n个长度为L的序列组成,定义其位置频率矩阵为

式(3)用于表示PWM1生成PFM2的可能性,其中 Alignment(1,2)是通过固定 PWM1、滑动 PFM2得到的矩阵列的比对.图1为PFM在PWM上的滑动示意图.
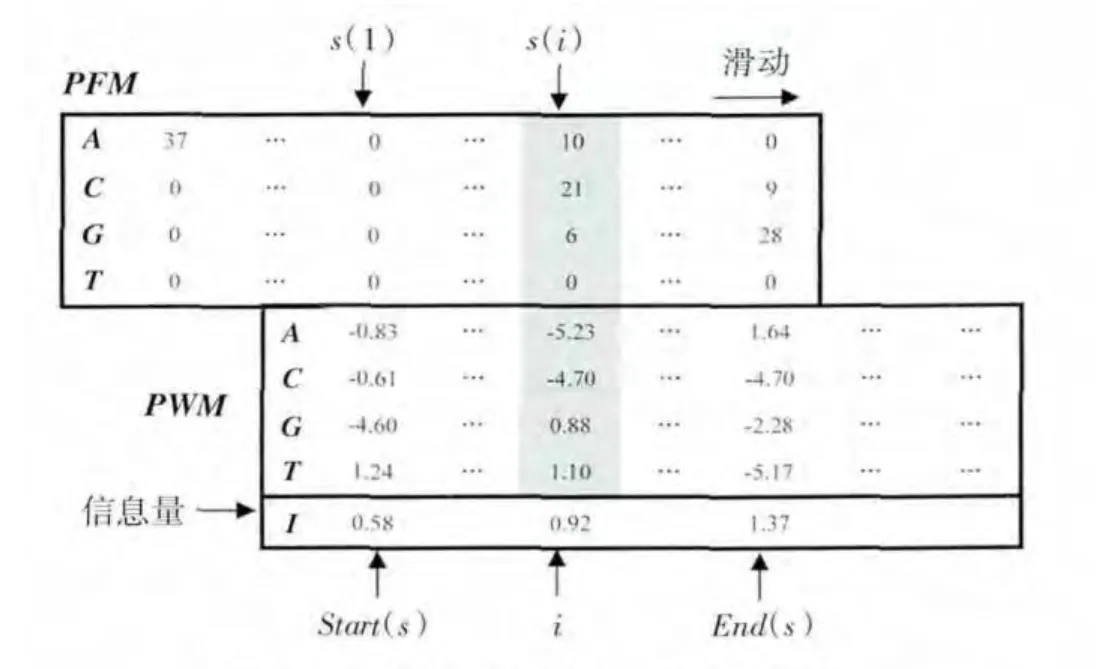
图1 PFM在PWM上的滑动示意图Fig.1 Representation of PFM sliding on PWM
由图1可以看出,当用PFM在PWM上逐列由左向右滑动形成比对s时,在该比对s中,PWM的第i列与PFM 的第 s(i)列对应.
再用Motif2的PFM2和Motif1的PWM1进行比对,计算相似性:

1.2 算法验证
为了验证算法的性能,利用经过验证的3个数据集对ICBSM进行测试和评估.数据集-1由Mahony等[3]从JASPAR库中首次选出,该数据库由96个真实的模体组成,这些模体属于13个已知的不同结构的TF类.文献[6]创建了数据集-2,用以测试KFV度量法对于识别冗余的位置频率矩阵的显著性能.该数据集由124个JASPAR的核心模体及每个核心模体的3个子模体组成,这些子模体通过随机选取每个模体的2/3序列得到.数据集-3可由http://gleclubs.uncc.edu/pbs页面下载,包含了大约105个假定的模体[18-19],这些模体来自大肠杆菌2000多组全基因组的同源基因间序列以及其他54个γ-变形菌门的参照基因组.关于3个数据集的详细参数参见表1.
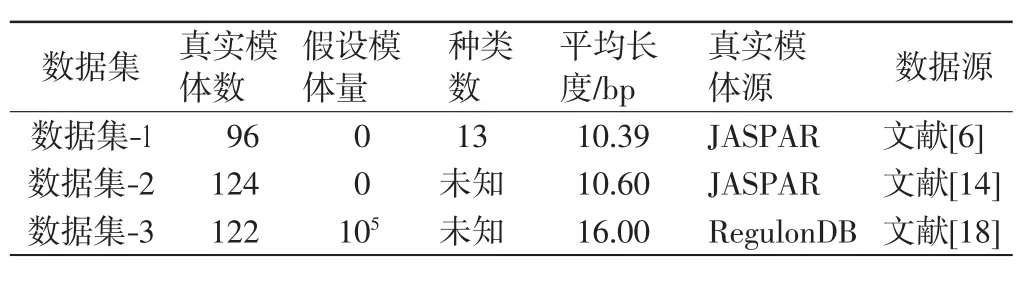
表1 用于测试与评估的3个数据集的参数Tab.1 Parameters of three datasets for testing and assessing
将ICBSM算法、STAMP工具包中的5个算法(ALLR,AKL,SSD,pCS,PCC)、KFV 法以及 Mosta算法中的AC应用到1个数据集上,针对聚类相关的真模体、过滤伪模体和找回模体等方面进行性能比较.利用STAMP平台计算5个依靠比对的度量法得分(http://www.benoslab.pitt.edu/stamp/),Mosta包计算AC得分(http://mosta.molgen.mpg.de),KFV的网络服务器计算KFV得分(http://bioinfo.uncc.edu/kfv/).
1.2.1 模体找回
带有比对算法的列相似度度量法和非比对相似度度量法可以用于将待查模体与数据库中的每一个模体进行比较,从而找回模体.如果在1个数据集中模体的相似度分数超过阈值,则表明这些模体被待查模体“命中”;如果有多个“命中”[6],则相似度分数最高的“命中”称为“最佳命中”.通过使用“最佳命中法”把在数据库中搜索模体的正确找回率定义为度量法的“性能精确度”.
与其他3个带有最优比对[6]的列相似度度量法和非比对度量的AC法[14]相比,SSD、PCC和KFV度量法在查找模体时具有更高精确度,因此选出它们与ICBSM度量法进行对比,比较它们在数据集-1中找回同一个转录因子家族模体的能力.在数据集-1上,STAMP包的5个带有比对设置的列相似度度量法中,结合SW的非空位比对算法PCC(PCC/SWU)和结合SW、空位延伸为0.5、空位开放为1的比对算法SSD/SW是最好的2个度量法和比对设置[7].根据文献[6]的描述,当把4-mer和夹角余弦值用于向量构建和比较时,KFV会获得最优结果.
本研究利用 ROC(receiver operating characteristic)曲线考察度量法在数据集-1和数据集-2中识别出相同转录因子的模体的性能.ROC曲线的绘制方法依据下述规则:给定1个由n个模体组成的数据集,其中这些模体的转录因子结构类已知,n个模体具有n(n+1)/2个组对,应用度量法分别计算出每一对的相似度分数.如果2个模体的相似度分数小于1个阈值或大于阈值但没有“最佳命中”,则设定这2个模体为错误匹配,否则为正确匹配.如果由度量法计算出2个模体正确匹配,且这2个模体确实同属于1个转录因子,则该正确匹配称为“真阳性(true positive,TP)”,否则这个正确匹配为“假阳性(false positive,FP)”;如果2个模体由度量法计算出是错误匹配,且这2个模体确实属于不同的转录因子,则该匹配称为“真阴性(true negative,TN)”,否则这个错误匹配为“假阴性(false negative,FN)”.ROC曲线是在不同的模体相似度阈值下由真阳性率对比假阳性率的描述.
1.2.2 从混杂的模体中分离出真模体
一些基于遗传系谱印技术的转录因子绑定位点的全基因组测序算法需要把任意转录因子的子模体和冗余模体合并成一个独立的模体并剔除伪模体[8-9,13],即聚类相似模体,区分出不相关的模体.因此,研究人员需要一个不仅能精确计算出一对模体的精确度,而且还能有效区分出无关模体的度量法,这个算法可以为相同转录因子模体的2个子模体赋予足够高的相似度值,为没有任何进化关系的2个模体赋予足够低的相似度值,从而在混杂的模体中分离出真模体.由GLECLUBS生成的数据集-3[8]由大量的混杂模体和一小部分的真模体构成,为从数据集-3中发现真模体,在Regulon数据库中选出一组真模体用于在数据集-3上进行评估.该组真实模体是大肠杆菌的122个转录因子模体生成的大量的真的子模体.每个转录因子模体均是由n个结合位点构成(n≥3),度量法把每个转录因子模体随机分成1个大小为k的子模体和1个大小为(n-k)的子模体,其中 k∈{1,2,…,[n/2]}.因此,每个大小为n的模体都可以生成[n/2]对的子模体.度量法对每个大小为k的子模体重复前面的分离过程,生成[k/2]对子模体的子模体.当每个子模体的大小为1时,过程停止.然后,利用这些度量法计算每对子模体间的相似度值[7,11],并在数据集-3上计算每对模体的相似度值.通过计算数据库-3中每对模体相似度分数标准化后的分布和每对真的子模体的相似度分数标准化后的分布,查看2个分布的重叠区域.
2 ICBSM算法性能分析与结果
2.1 模体找回
对于从一个数据集中找回模体,本研究将模体比较的阈值设置为0.6,然后将ICBSM、KFV、PCC/SWU和SSD/SW算法在数据集-1上计算精确度,结果如表2所示.
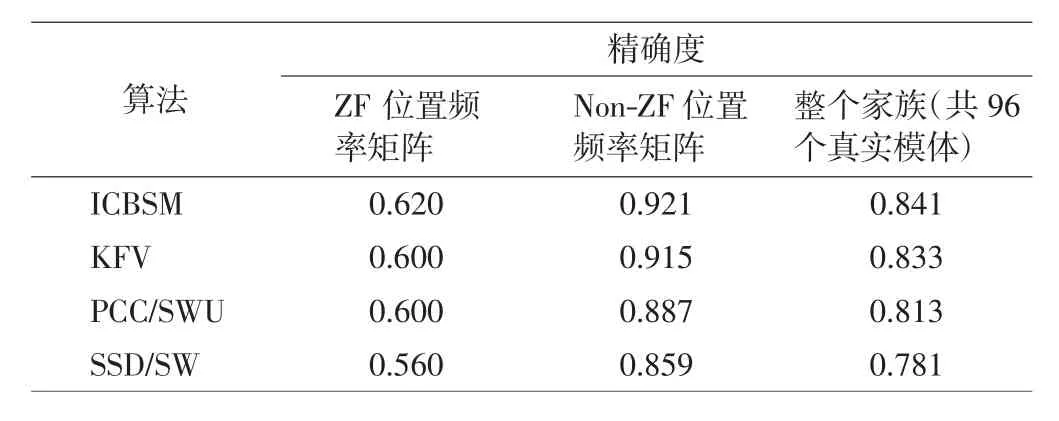
表2 在数据集-1上,ICBSM、KFV、PCC/SWU及SSD/SW模体找回的精确度Tab.2 Accuracy for searching motifs of ICBSM,KFV,PCC/SWU and SSD/SW on dataset-1
数据集-1可以分为包含25个真实模体的锌指状结构蛋白质家族(zinc-finger,ZF)和包含71个真实模体的非锌指状结构蛋白质家族(non-ZF).由表2中结果可知,对于ZF蛋白质家族、Non-ZF蛋白质家族以及整个蛋白质家族集合,ICBSM算法的模体找回精度最高,说明该算法在数据库中能够正确找回模体的能力最强,比其他3种度量法具有更卓越的策略.
为了将ICBSM与PCC/SWU、KFV(4-mer夹角余弦值)的最优策略做进一步比较,在模体比较阈值设置为0.6的情况下,在数据集-1和数据集-2上,对这3种策略的性能进行ROC分析,结果如图2所示.由图2可知,假阳性率相同的情况下,ICBSM度量法的真阳性率最高,即对于同1个数据集,ICBSM度量法能够正确找回模体的能力比其他2种方法更强.

图23 种度量法的ROC曲线图Fig.2 ROC curves of three metrics
2.2 从混杂的模体中分离出真模体
用ICBSM度量法、STAMP工具包、AC度量法以及KFV度量法分别计算数据集-3的每对模体相似度分数以及每对真的子模体的相似度分数,并将这2个分数标准化形成曲线分布图,以ICBSM度量法与AKL度量法曲线分布效果为例,结果如图3所示.
图3中“数据集-3模体”的曲线是在数据集-3中计算每对模体相似度分数标准化后的分布曲线,标有“真的子模体”曲线是每对真的子模体的标准化相似度分数的分布曲线.在数据集-3中,由于每对真的子模体具有相关性而大多数模体具有无关性,因此性能好的度量法应该可以把前一个相似度分布区域与后一个相似度分布区域分离出来,即图3中2个曲线所围成的2个区域的重叠部分越小,分离效果越好.ICBSM在计算模体的相似度分数时考虑了信息容量,因此可以从带有低信息容量的混杂的模体中分离出真模体.
将ICBSM与其他度量法生成的相似度分布曲线的重叠区域比率进行比较,结果如图4所示.在ICBSM的分布曲线下,2块区域具有最小的重叠部分,这说明与其他度量法相比,ICBSM能够更加精确地从混乱模体中分离出真模体.
3 结论
在生物信息处理过程中,由于很多应用都包含了模体比较的过程,因此提出一种基于列信息内容的用于模体比较的非比对度量法ICBSM,通过对比分析,结果表明:
(1)ICBSM度量法采用了带有信息容量的非比对策略计算模体间的相似度分数,将信息容量添加到模体的位置赋权矩阵上,将一个模体的位置频率矩阵在另一个模体的位置赋权矩阵上滑动,计算2个模体间的相似度.该算法依赖参数少,提升了计算效率.
(2)在模体比较的阈值设置为0.6的情况下,在数据集-1上,ICBSM度量法与KFV、PCC/SWU及SSD/SW相比较,其模体找回的精确度最高;同时,与KFV、PCC/SWU相比较,ICBSM的ROC曲线的真阳性率值也最高,这说明该方法在数据库中找回模体的效果更好.
(3)由于ICBSM在计算模体相似度时考虑了模体的信息容量,因此它计算出的真的子模体的相似度分数标准化后的分布曲线与数据集中所有模体的相似度分数标准化后的分布曲线重叠率最低,说明该方法能够精确地将真模体从混杂的模体中区分出来,为聚类相似模体、分组不相关模体提供了有效工具.
[1]CELNIKER S E,DILLON L A,GERSTEIN M B,et al.Unlocking the secrets of the genome[J].Nature,2009,459(7249):927-930.
[2] RISTER J,DESPLAN C.Deciphering the genome's regulatory code:the many languages of DNA[J].Bioessays,2010,32(5):381-384.
[3] REED J L,FAMILI I,THIELE I,et al.Towards multidimensional genome annotation[J].Nat Rev Genet,2006,7(2):130-141.
[4]ALEXANDER RP,FANG G,ROZOWSKY J,SNYDER M,et al.Annotating non-coding regions of the genome[J].Nat Rev Genet,2010,11(8):559-571.
[5] GUHATHAKURTA D.Computational identification of transcriptional regulatory elements in DNA sequence[J].Nucleic Acids Res,2006,34(12):3585-3598.
[6] STORMO G D.DNA binding sites:representation and discovery[J].Bioinformatics,2000,16(1):16-23.
[7]MAHONY S,AURON PE,BENOS P V.DNA familial binding profiles made easy:comparison of various motif alignment and clustering strategies[J].PLoS Comput Biol,2007,3(3):61.
[8]SANDELIN A,WASSERMAN W W.Constrained binding site diversity within families of transcription factors enhances pattern discovery bioinformatics[J].J Mol Biol,2004,338(2):207-215.
[9] WANG T,STORMO G D.Identifying the conserved network of cisregulatory sites of a eukaryotic genome[J].Proc Natl Acad Sci USA,2005,102(48):17400-17405.
[10]SCHONES D E,SUMAZIN P,ZHANG M Q.Similarity of position frequency matrices for transcription factor binding sites[J].Bioinformatics,2005,21(3):307-313.
[11]WANG T,STORMO G D.Combining phylogenetic data with coregulated genes to identify regulatory motifs[J].Bioinformatics,2003,19(18):2369-2380.
[12]KULLBACK S,LEIBLER R A.On information and sufficiency[J].Ann Math Statist,1951,22(1):79-86.
[13]PIETROKOVSKI S.Searching databases of conserved sequence regions by aligning protein multiple-alignments[J].Nucleic Acids Res,1996,24(19):3836-3845.
[14]XU M,SU Z.A novel alignment-free method for comparing transcription factor binding site motifs[J].PLoS One,2010,5(1):87-97.
[15]NEEDLEMAN S B,WUNSCH C D.A general method applicable to the search for similarities in the amino acid sequence of two proteins[J].J Mol Biol,1970,48(3):443-453.
[16]SMITH T F,WATERMAN M S.Identification of common molecular subsequences[J].J Mol Boil,1981,147(1):195-197.
[17]MAHONY S,BENOS P V.STAMP:a web tool for exploring DNA-binding motif similarities[J].Nucleic Acids Res,2007,35:253-258.
[18]ZHANG S,XU M,LI S,et al.Genome-wide de novo prediction of cisregulatory binding sites in prokaryotes[J].Nucleic Acids Res,2009,37(10):72.
[19]ZHANG S,LI S,PHAM P T,et al.Simultaneous prediction of transcri-ption factor binding sites in a group of prokaryotic genomes[J].BMC Bi-oinformatics,2010,11:397.

