基于多体动力学的连杆强度分析

秦飞 贾德文 毕玉华 申立中

（昆明理工大学云南省内燃机重点实验室云南昆明650500）

基于多体动力学的连杆强度分析

秦飞 贾德文 毕玉华 申立中

（昆明理工大学云南省内燃机重点实验室云南昆明650500）

连杆作为发动机最重要的零部件之一，工作过程中受急剧变化的动载荷影响，容易发生断裂失效，必须具有较高的强度和可靠性。采用多体动力学仿真进行边界条件求解，确定连杆的最大压载荷和最大拉载荷，在此基础上进行静强度计算得到三个工况下的应力分布，计算出危险截面的安全系数。分析结果表明连杆在4000 r/min时承受载荷最大，在此工况下应力集中截面为连杆小头与杆身过渡处、连杆大头与杆身过渡处、油孔及小头孔内部下半部分，最大应力值为641Mpa，在材料许用应力范围内。几个危险截面中安全系数最小为1.34，设计安全，并具有一定的强度储备。

连杆多体动力学强度安全系数

引言

连杆作为发动机曲柄连杆机构中的重要零部件，将活塞的往复直线运动转换为曲轴的旋转运动，使作用在活塞上的燃气力传递给曲轴来对外输出。其运行工况相当复杂整体承受着压缩、拉伸和弯曲等交变载荷[1]。一旦连杆发生断裂失效，将使整机受到严重破坏。因此进行强度校核和安全系数的计算已成为连杆设计中必不可少的步骤[2，3]。

在连杆的静力学计算中，大多通过经验公式计算几个危险工况下连杆所承受载荷。这里通过建立连杆和缸套的刚柔耦合模型，考虑了油膜润滑条件，获取作用在连杆上一个周期内的循环载荷[4]。恢复连杆在多体动力学[5]计算中所忽略的特征，建立三维多体装配模型来模拟位移边界条件，用接触对来模拟零件间的连接关系来传递力和力矩，将多体动力学计算所得的边界条件加载于连杆上，计算得到与实际较为吻合的应力分布规律和变形趋势，根据应力求出几个危险截面安全系数来判断该设计的合理性。该研究方法提高了连杆结构设计的合理性，为结构设计和改进提供了理论依据，达到了分析的目的。

1 多体动力学仿真

多体动力学仿真是指对通过一定方式相联接的多个物体（包括刚体弹性体、柔性体、质点等）构成的系统进行准确地分析求解的过程[6，7，8]。

1.1 连杆柔性体模型

连杆在多体动力学仿真中是主要计算的对象，其为复杂的弹性连续体，它的弹性特征对整个多体动力学计算影响比较大。本文是通过有限元子结构缩减得到连杆的柔性体模型的。

通过UG进行连杆三维实体模型的建模，忽略小头油孔特征。利用HYPERMESH对连杆进行网格划分、RBE2约束及材料属性的赋予等前处理，连杆体模型采用四面体8节点单元；衬套和轴瓦采用六面体8节点单元，在轴线方向上均匀生成7个节点，小头在圆周方向上生成60个节点，大头在圆周方向上生成80个节点，并应用RBE2单元对连杆的小头建立MPC约束。

1.2 刚柔耦合模型的建立

为了计算发动机工作过程中连杆各节点的载荷，需要建立连杆机构的刚柔耦合模型。分析模型包括缸套、曲柄销、活塞销、连杆整体模型和连杆轴承。其中，曲柄销和活塞销模型均采用五个质量点代替；缸套用刚体代替；连杆轴承采用ehd2类型的轴承模型，该模型充分考虑了非线性油膜特性、轴承几何形状、轴瓦变形和机油填充率等对轴承性能的影响。该连杆的EXCITE动力学模型如图1所示。

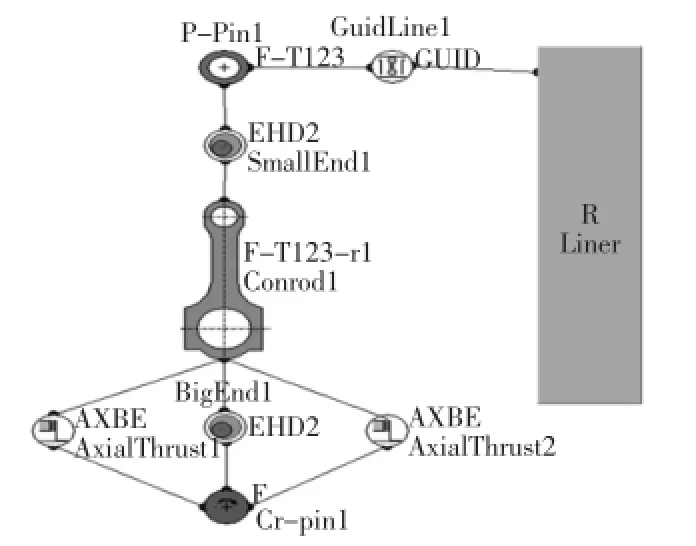
图1 曲柄连杆机构二维模型

1.3 多体动力学计算结果

基于某发动机不同转速下缸压测试数据，选取转速1000 r/min、2000 r/min、3000 r/min、4000 r/min四个转速，缸压曲线如图2所示：

图2 缸压曲线

最大爆发压力发生在4000 r/min，最大接近16 MPa。在AVL-EXCITE软件中将机油类型，缸内压力曲线和供油压力等数据输入后进行计算。仿真一个工作循环，仿真步数720步，得到连杆小头的载荷曲线如图3所示。

图3 连杆载荷曲线

2 有限元仿真

有限元计算模型包括活塞、连杆体、连杆盖、活塞销、衬套、轴瓦、螺栓、曲轴。由于分析对象为连杆体与连杆盖，建模时除连杆体与连杆盖，其它部件做必要的简化。选取最大拉伸、最大压缩、装配三个工况进行相应计算。

2.1 网格划分

运用ABAQUS前处理模块对各部件进行网格划分。在网格划分时，对于形状较简单的活塞销、曲柄销采用六面体网格进行划分。其他的零件皆采用一阶四面体网格进行划分。由于连杆在小头与杆身过渡处、大头与杆身过渡处、小头油孔和大头凸台存在应力集中，此处采用较精细的网格来提高网格质量，使计算结果更趋精确。为加快收敛速度和降低对计算机的硬件要求，其他部件则采用相对较大的网格来划分。建立接触对如表1所示。

表1 创建的接触对

2.2 装配工况计算

连杆组件只受连杆螺栓预紧力、衬套过盈装配预紧力、轴瓦过盈装配预紧力，观察在非工作状态下连杆大小头的变形模式。

2.2.1 螺栓预紧力

通过均匀分布在连杆螺栓螺杆端面的力模拟螺栓预紧力。螺栓拧紧力矩计算公式为：

式中：T为螺栓安装时的拧紧力矩，kt由经验得到，d为螺栓的直径，通过计算得到螺栓的预紧力F= 41602 N。

2.2.2 连杆小头过盈量

连杆小头直径为a，上偏差为0.01 mm，下偏差为-0.01 mm；连杆小头衬套直径为a，上偏差为0.062 mm，下偏差为0.046 mm。计算并取平均值可得连杆小头径向过盈量为0.054 mm。

2.2.3 连杆大头过盈量

轴瓦压缩量计算公式为：

式中：F为轴瓦装配力，d为大头轴孔内径，公差为Δ，E为材料弹性模量，f为摩擦系数，余面高度：u= 0.08～0.12 mm，轴瓦宽度为L，轴瓦厚度为t。计算并取平均值可得轴瓦径向过盈量为0.0956 mm。

2.3 边界约束与载荷的施加

装配工况过盈量通过计算得到，从多体动力学计算结果提取最大拉压载荷。在活塞顶面建立MPC，通过MPC约束，将一个点上的受力传递给活塞顶面的每一个节点，由活塞与活塞销、活塞销与连杆小头的接触将力传递给连杆小头，从而引起连杆体的应力和形变。这种加载方法有助于载荷的施加，并且与连杆受力的真实情况相近。

计算模型的刚体位移约束采用如下方法：连杆大头孔通过轴瓦与曲轴连接，曲轴两端面采用全约束；对活塞销断面一节点施加点对地的Z方向上的弹性约束来进行位移协调。结果如图4所示：

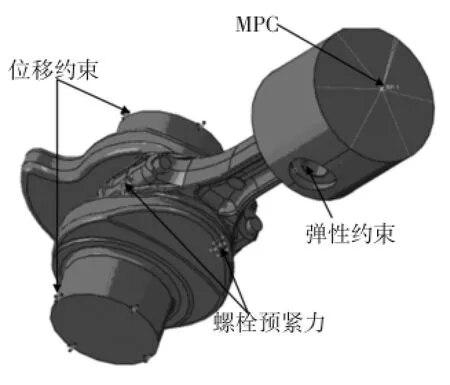
图4 边界条件及载荷

3 计算结果分析

在4000 r/min时连杆承受载荷情况最为恶劣，得到4000 r/min时三种受力工况下连杆大小头和连杆盖的应力云图和位移云图，根据材料属性判断危险截面，并求得危险截面的疲劳安全系数。材料属性见表2。

表2 材料属性

3.1 装配工况

图5为装配工况下的连杆体和连杆盖的应力云图，从图中可以看出连杆小头处的油孔和连杆盖跟螺栓连接的位置应力较为集中。

图5 装配应力

图6是连杆大头孔在预紧力和轴瓦过盈配合作用下的变形趋势。从中可以看出，连杆大头孔在轴瓦过盈预紧力和螺栓预紧力的作用下，大头孔呈现出沿连杆纵向压扁，横向伸长的变形模式，但整个大头孔的变形量较小。

图6 大头变形

图7为在衬套过盈预紧力的作用下，连杆小头的受力云图。从图中可以看出，在衬套过盈预紧力作用下，连杆小头受力主要集中在连杆小头油孔处，小头孔内部上半部分受力比下半部分大，油孔处的等效应力最大值为424 MPa。

图7 油孔应力

3.2 最大拉伸工况

在最大拉伸工况下，连杆最大集中应力发生在连杆小头油孔处、连杆盖和螺栓连接的位置。图8是连杆在最大拉伸工况下，小头油孔处的应力云图。

从图中得出油孔处的最大应力值为142.3 MPa，并且在小头与杆身过渡处的应力也相对较大。

3.3 最大压缩工况

图9是连杆在最大压缩工况下的应力图。在最大压缩工况下，连杆最大应力发生在连杆小头孔下部，其值为641.5MPa，同时连杆小头与杆身过渡处、大头与杆身过渡处应力也都较大，应力值为481.6MPa左右。连杆的材料采用调制钢，许用应力为735 MPa，危险截面的最大应力值均小于材料的许用应力。

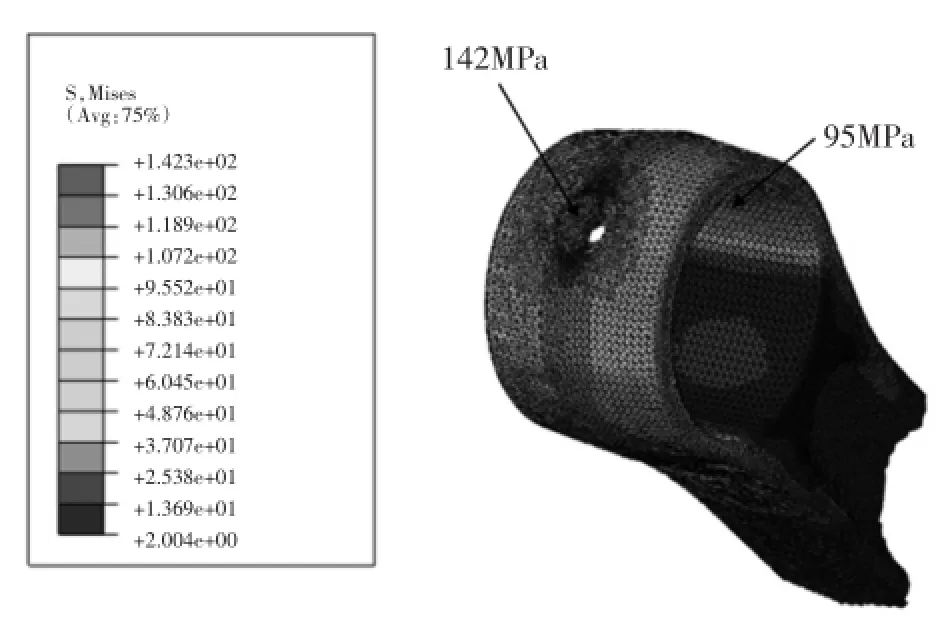
图8 小头应力

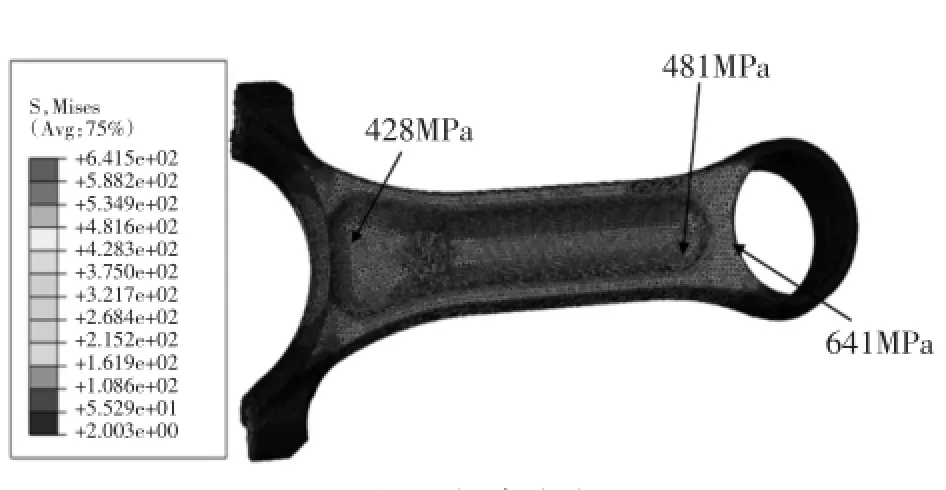
图9 杆身应力

3.4 安全系数计算

连杆失效多为在周期性变化的外力作用下所产生的疲劳破坏。根据计算结果可知，连杆小头油孔、小头与杆身过渡处、大头与杆身过渡处所受的应力水平比较大，因此对这几个地方疲劳强度进行校核。用基于Von Mises屈服条件计算小头的疲劳安全系数。

所使用的安全系数求解公式为：

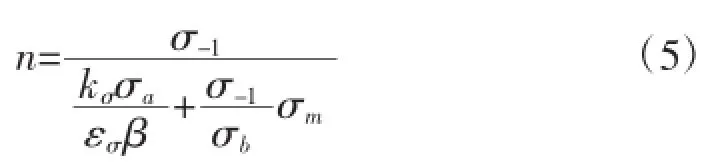
其中：σb为材料的抗拉强度；σs为材料的屈服强度；σ-1为材料的疲劳极限，应力幅σa；σm为平均应力；kσ为应力集中系数，油孔处取为2，过渡处取为1；表面工艺影响系数β为1.5；尺寸影响系数εσ为1。

通过计算得到几个危险截面的安全系数见表3。

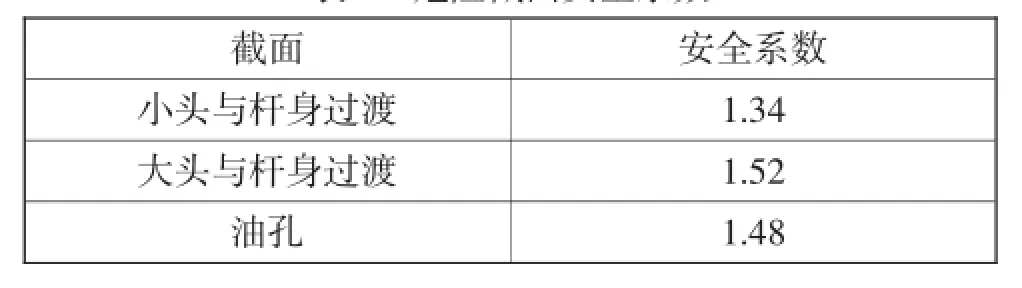
表3 危险截面安全系数

抗疲劳许用安全系数值取决于应力计算的可靠性、材料的均匀性、零件的制造工艺水平及其他一些因素，这里安全系数许用值取n=1.0～1.2。通过比较，几个危险截面处的疲劳安全系数皆大于该许用值，即可以判断连杆工作可靠。所以连杆的结构设计满足疲劳强度的要求。

4 结论

多体动力学计算忽略了连杆的一些特征，比如油孔等。有限元静强度计算的边界条件不太准确。将两种方法结合在一起，能更有效地仿真连杆工作情况。

1）在装配工况下，连杆盖的凸台和连杆小头油孔是应力较为集中的地方，最大应力出现在连杆凸台位置，大小为424 MPa，小于材料的许用应力值。在拉伸工况下，连杆小头油孔是应力较为集中的部位，大小为424 MPa，在材料的许用应力之内。在最大压缩工况下，连杆小头内部下半圆、大小头与杆身过渡处是应力集中的地方，最大应力出现在小头内部下半圆，大小为641 MPa，在材料的许用应力范围之内。

2）计算了疲劳载荷作用下三个危险截面的安全系数，连杆小头与杆身处的安全系数为1.34，油孔处的安全系数为1.52，大头与杆身处的安全系数为1.48，均大于最大安全系数许用值1.2。证明了连杆各个部分的安全系数均在设计允许范围内，连杆的结构设计是安全的，并且具有一定的强度储备。

3）针对此次有限元的分析结果，在以后设计连杆结构的时候，重点考虑连杆三个受应力较为严重的部位，通过相应结构优化来减少此处的应力集中。比如小头壁厚加大，大小头与杆身过渡圆弧适当地加大一些。

1吕彩琴，苏铁熊.柴油机连杆的有限元疲劳强度分析[J].华北工学院学报，2002，23（1）：15～19

2宋晋宇.柴油机连杆螺栓预紧力的数值分析[J].柴油机设计与制造，2006，14（2）：27～31

3李燕，袁志华，曾俊华.基于ABAQUS的4V-105柴油机连杆有限元分析[J].机械传动，2010，34（8）：39～42

4屠丹红，姜树李，曹茉莉.498连杆组件的有限元分析[J].内燃机学报，2004，22（2）：176～181

5王晓.曲柄连杆机构多体系统动力学与油膜动力润滑耦合仿真研究[J].内燃机，2010（1）：1～3

6何柏岩，陈寺专，裴毅强，等.基于多体动力学的479Q发动机连杆载荷与强度分析[J].内燃机工程，2011，32（4）：39～45

7Knoll G，Lang J，Rienäcker A.Transient EHD connecting rod analysis：full dynamic VS.Quasi static deformation[C]. 1995 STLA/ASME Tribology Conference，Kissimmee，Florida，Oct 8.1995

8Kim B J，Kim K W.Thermo-elastic hydrodynamic analysis of connecting rod bearing in internal combustion engine[J]. Journal of Tribology，2001，123（3）：444～454

The Strength Analysis of Connecting Rod Based on Multi-body Dynamics

Qin Fei，Jia Dewen，Bi Yuhua，Shen Lizhong
Yunnan Key Laboratory of Internal Combustion Engine，Kunming University of Science and Technology（Kunming，Yunnan，650500，China）

Connecting rod is one of the most important parts of engine，and it works under a sharp change of dynamic load，which makes it easy to fracture failure，it is very serious.Therefore，connecting rod must have high strength and reliability.This article adopts the method of multi-body dynamics，to determine the maximum compression conditions and the maximum tensile conditions，and calculate safety factor of several dangerous section.The results show that the maximum force is at 4000rpm，and the concentration section appears at the transition area for big end of connecting rod and shaft，small end of connecting rod and shaft，the lower half of the oil hole and small end.Maximum stress value is 641Mpa，it is under the range of allowable stress value.The minimum safety factor is 1.34 in the several dangerous section，the design has some strength reserve.

Connecting rod，Multi-body dynamics，Strength，Safety factor

TK412+.4

A

2095-8234（2014）05-0055-05

2014-09-01）

秦飞（1987-），男，硕士研究生，主要研究方向为连杆断裂失效仿真与试验研究。

贾德文（1977-），男，副教授，博士后，主要研究方向为内燃机结构设计与优化。