基于突变理论的滑坡危险性评价

宋盛渊，王 清，潘玉珍，陈剑平，项良俊

（1.吉林大学 建设工程学院，长春 130026；2.长江三峡勘测研究院有限公司，武汉 430010）

1 引言

随着我国西南地区水电工程的发展和人类经济活动不断加剧，滑坡灾害的发生给人类生命和财产造成了严重的危害，如何科学有效地评价滑坡的危险性，是滑坡灾害研究中的一个重要课题。1994年初乔建平等[1]采用数学统计的方法，对长江上游滑坡进行了危险度区划研究。1994年底唐川等[2]采用模糊综合分析法对云南省滑坡进行了危险度区划研究。两项研究均是对区域滑坡危险性的评价研究，未对单体滑坡危险性进行评价。

为了评价单体滑坡的危险性，王成华等[3]建立了高速滑坡危险度判别模型。樊晓一等[4]利用层次分析法，建立了滑坡危险度评价指标，确定了滑坡危险度等级。杨宗佶等[5]利用信息熵原理，求取各评价指标的客观权重，并以此建立了滑坡危险性评价模型。李军霞等[6]采用组合赋权与未确知测度理论建立了滑坡危险性评价模型。上述研究都是对滑坡评价因子赋予了权系数或作用指数之后综合评价的，在赋予权系数或作用指数的过程中都具有不同程度的主观性，本文引入了一种新的滑坡危险性评价方法——突变级数法。

突变级数法将突变理论与模糊数学结合起来，故又称突变模糊隶属函数[7]。这种方法虽然没有对各评价指标采用权重值，但权衡了各评价指标的相对重要性。采用定性与定量相结合的方法，既减少了主观人为性，又不失科学性和合理性，且该方法简单、准确，可适用于多目标的评价与决策。

2 突变级数法的基本原理

突变级数法的基本思想是将所研究系统的评价指标进行多层次分解，排列成倒立的树枝状结构。将最底层的控制变量代入相应的突变模型中进行归一化计算，并按照“互补”或“非互补”原则计算出该层的突变级数。最后，逐层向上计算各层的突变级数，并根据最高层的突变级数将所研究的系统分级。突变级数法的主要步骤如下[8－9]。

（1）建立逐层结构模型

根据系统的内在作用机制，将总指标进行多层次主次矛盾分解，先主后次排列成倒立的树枝状结构。逐层向下分解，直至分解到可以计量的指标为止。常用的分解形式如图1所示。图中，x为状态变量；u、v、w、t为控制变量。

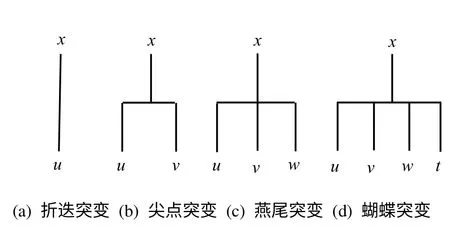
图1 突变模型系统Fig.1 Catastrophe model system

（2）评价指标的无量纲化处理

由于最底层评价指标之间的取值范围和单位量纲均不相同，各指标之间无法进行比较，需将其转变为0～1之间的无量纲数据。同时，还需将所有的评价指标数据转化为“越大越好”型数据，对“越小越好”型数据可采用倒数法进行标准化处理。

（3）归一化公式的推导

突变系统的势函数为F(x)。通过对F(x)求一阶导数，并令 F ′(x)=0，可得到它的平衡曲面；通过对F(x)求二阶导数，并令 F ′(x)=0，可得到平衡曲面的奇点集；由方程 F ′(x)=0和 F ′(x)=0联立求解，可得分歧方程。当各控制变量满足分歧方程时，系统将发生突变。通过分解形式的分歧方程可导出归一化公式，由归一化公式将各控制变量的不同质态化为同一质态，即化为由状态变量表示的质态。常用的几种突变模型见表1[10]。

表1 初等突变类型Table 1 Catastrophe model

（4）突变级数的计算

确定控制变量的数目后就可以选择对应的初等突变模型，根据不同模型的归一化公式和最底层评价指标的无量纲数据，可计算诸控制变量的中间值，即突变级数值，计算过程中若指标之间无相关性采用“非互补”原则，即“大中取小”；若指标之间具有相关性应采用“互补”原则，即“取平均数”。逐层向上计算突变级数，最终求出总突变级数进行评价。

3 研究区概况及滑坡影响因素

3.1 研究区概况

岩桑树水电站位于云南省保山市境内的怒江下游干流上，工程区范围上游至三达地漫海桥（怒江大桥），下游至三江口一带。库区为横断山系切割山地狭谷区，属中山-高山地貌，怒江位于南北向延伸的山脉间，其东侧为怒山山脉，西侧为高黎贡山山脉。山岭高程大多集中在1 600～2 600 m。河谷高程为605～650 m，切割深度一般都大于1 000 m，属于深切割河谷。库区内地下水根椐地下水赋存条件、水力学特征和水理性质，划分为松散岩类孔隙水、碳酸盐岩类喀斯特水、基岩裂隙水3种类型。库区内褶皱主要分布于怒江左岸，有湾子铺-上新寨向斜、金刚园背斜、大坪子背斜、大井脚向斜和垭口向斜，多呈南北向展布，右岸仅发育一个褶皱，为团树梁子向斜。工程区域内的地层按照岩石的成因分为变质岩分布区、花岗岩分布区及沉积岩分布区，其中沉积岩按沉积分带及沉积环境的变化特征可大致分为绕廊街等养沉积区、怒江河谷沉积区、牛旺街沉积区及海相侏罗系沉积区。通过现场调查，综合确定库区两岸分布有22个潜在滑坡，包括古(老)滑坡、崩堆积体、具有滑坡趋势的斜坡，比传统滑坡概念更加广泛，岩桑树区域地层分布图见图2。

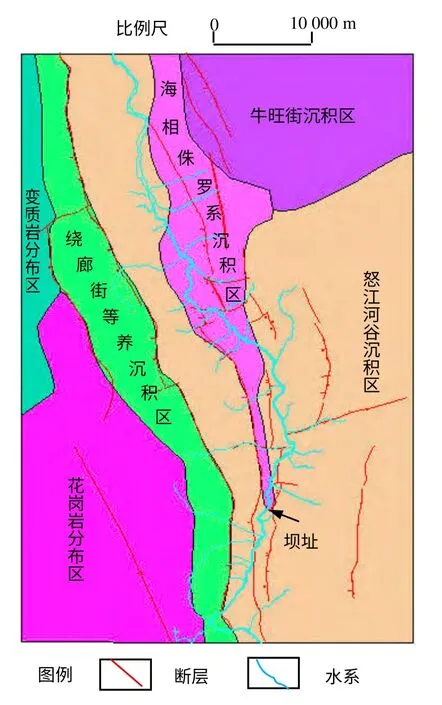
图2 岩桑树区域地层分布图Fig.2 Formation distribution map of Yansangshu area

3.2 评价指标的选取

影响滑坡危险性的因素众多，为了体现出评价指标的选取具有全面性、代表性、科学性和实用性的原则，本文参照国内外专家常采用的滑坡影响因素[11]，综合考虑研究区内滑坡成因、空间分布的特征，同时兼顾选取的评价指标易于定量化，从地质条件、滑坡特征、诱发因素为基本出发点，提取了具有普遍意义的9个因素作为滑坡危险性评价指标。各影响因子的选取依据如下。

（1）坡体风化程度（D1）

坡体风化程度越高，表明岩体相对破碎，节理裂隙发育，坡体稳定性差，同时为地下水提供流通路径，进一步促进坡体不稳定性。

（2）地层岩性（D2）

作为坡体的物质组成，岩层性质及其组合形式对坡体稳定性起到很大的控制性，尤其要注意区分岩层软硬组合形式。

（3）坡体到断层距离（D3）

断层的存在会使附近一定范围内的岩体遭到破坏，从而降低了坡体的完整性，同时作为重要的地下水通道，会给坡体的变形和破坏带来不利影响。

（4）坡面倾向（D4）

滑坡发育的坡向不同，受太阳光照的时间不同，地表温度导致的风化作用与程度也不同。相同的岩性条件，阳坡风化程度会强于阴坡和半朝阳坡。

（5）植被覆盖率（D5）

当坡面植被大量发育时，植物的根系加强了坡体的整体性，同时植被发育，可防止坡面松散物质流失，阻止降雨入渗，有利于坡体的稳定。

（6）斜坡坡度（D6）

坡体的坡度对滑坡失稳的发生具有很大的控制性作用。坡度不同，不仅会影响坡体内部沿已有的或潜在的滑动面的剩余下滑力的大小，而且在很大程度上决定了坡体变形和破坏的形式与机制。

（7）斜坡高度（D7）

坡体高度是分析滑坡稳定性的重要影响因素，当其他条件基本相同时，坡高越大，剩余下滑力就越大，越容易产生滑坡。

（8）滑体体积（D8）

滑坡体积是表征滑坡特征的重要参数，研究表明，滑坡体积越大，其潜在的危险性越大。

（9）正常蓄水后坡体被浸没比例（D9）

水位变幅越大，作用范围也越大，则塌岸速率越大。

这9个评价指标对滑坡的危险性均起着关键的作用，且有些指标之间是互相影响、互相作用的，因此需要分析各评价指标间的相关性。研究区滑坡的各评价指标值见表2。

3.3 评价指标的相关性

科学合理地确定评价指标是评价工作的基础和关键，为计算突变级数时采用“互补”或“非互补”原则提供依据，应注意分析评价指标间的相关性。本文采用皮尔逊积矩相关系数法进行评价指标间的相关性检验。

（1）对评价指标值的标准化

由于各评价指标值的取值范围和单位量纲均不同，需消除不同计量单位对检验结果的影响，所以要对各评价指标值进行标准化处理，标准化计算式为

式中：xi为评价指标值；为评价指标标准化值；xmax、xmin分别为评价指标的最大值和最小值。评价指标中植被覆盖率D5和正常蓄水后坡体被浸没比例D9可以直接用小数表示，无需标准化。

表2 研究区滑坡的各评价指标值Table 2 Evaluation indices of landslide in study area

对于定性指标的标准化可以采用赋值的方式，如坡体风化程度越严重，岩体质量越差，所形成滑坡的危险性也越大。对于风化程度严重的坡体应赋予较大的值，反之，则赋予较小的值。同理，影响滑坡危险性从强到弱的岩层组合形式为软岩、软岩夹硬岩、硬岩夹软岩、硬岩[12]。根据有关研究，对于坡体风化程度D1和地层岩性D2的赋值见表3。

表3 定性指标的标准化值Table 3 Standardized values of qualitative indices

对于坡面倾向D4，属于适度指标，应采用式（2）进行标准化：

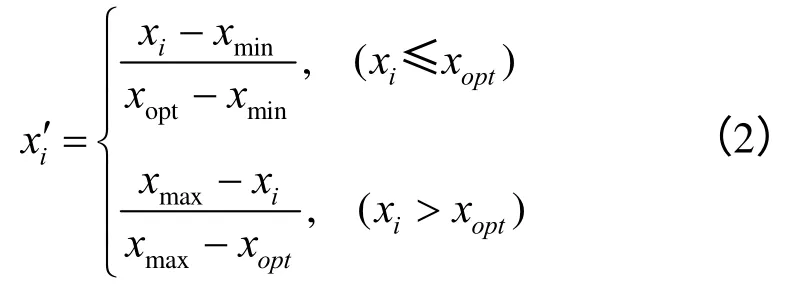
式中：xopt为适度指标的适度值。由于研究区滑坡沿近南北向的怒江两岸分布，因此坡面倾向的适度值取180°。

（2）计算各评价指标间的相关系数

计算两两评价指标之间的相关系数，皮尔逊积矩相关系数计算公式为[13]

表4 各评价指标间的相关系数Table 4 Correlation between every evaluation index

4 基于突变理论的滑坡危险性评价

4.1 建立滑坡危险性评价的突变模型

突变级数法的优点是无需计算各评价指标的权重值，只需将各层次评价指标按照相对重要程度进行排序。各层次评价指标的相对重要程度主要通过相应的归一化公式体现，相对重要的指标排在前面，次要的置于后面。

根据滑坡的现场调查资料、研究区的工程地质条件、滑坡的形成机制以及相关的参考文献，建立滑坡危险性评价的多层次突变模型见表5。

滑坡危险性评价的各评价指标取值范围和单位量纲均不相同，不能够相互比较，需对其进行标准化处理。同时，突变级数法要求最底层指标需转化成“越大越好”型指标。对于正指标，采用式（1）进行标准化；对于负指标，采用下式进行标准化：

式中：xi为评价指标值；为评价指标标准化值；xmax、xmin分别为各评价指标的最大值和最小值。坡体到断层距离D3、植被覆盖率D5属于负指标，应采用式（4）进行标准化。对于其他指标，应参照章节3.3进行标准化，但应注意的是 xmax和 xmin所指的最大值和最小值不再是仅待评价各滑坡的评价指标实测值中最大值和最小值，而是包括单指标各评价等级之间阈值在内的最大值与最小值。

4.2 确立评价等级标准

对于滑坡危险性等级的划分，尚未形成统一的标准。因此，本文参照国内外评价标准[5－6，14]，结合研究区滑坡实际地质特征，将滑坡危险性划分为轻度危险、中度危险、重度危险和极度危险4个等级，滑坡危险性评价指标的单指标危险性划分标准见表6。

表5 滑坡危险性评价突变模型Table 5 Catastrophe model of landslide susceptibility assessment

表6 研究区滑坡危险性分级标准Table 6 Classification standard of landslide susceptibility degree in study area

将滑坡危险性各等级的单指标值进行标准化，然后将其带入到滑坡突变模型中进行归一化计算，最终得到滑坡危险性的突变级数评价标准：轻度危险0～0.541，中度危险0.541～0.894，重度危险0.894～0.944，极度危险0.944～1.000。

4.3 突变级数的计算与评价结果

利用突变模型的归一化公式计算各层评价指标的突变级数，下面以1号滑坡的归一化为例进行阐述。

对于D1与D2有X1D=(0.625)1/2=0.791，X2D=(0.625)1/3=0.855。因为D1与D2间基本无相关性，按“非互补”原则，采用“大中取小”：

对于D6与D7有X6D=(0.140)1/2=0.374，X7D=(0.021)1/3=0.277。因为D6与D7间基本无相关性，按“非互补”原则，采用“大中取小”：

对于D3、D4、D5、D8、D9分别采用折迭型突变模型，有：C2=(D3)1/2=0.980，C3=(D4)1/2=0.866，C4=(D5)1/2=0.316，C6=(D8)1/2=0.224，C7=(D9)1/2=0。

同理，对于C1、C2、C3与C4采用“非互补”蝴蝶型突变模型，有B1=min{(C1)1/2、(C2)1/3、(C3)1/4、(C4)1/5}=0.794。

对于C5与C6采用“互补”尖点型突变模型，有：B2=average{(C5)1/2、(C6)1/3}=0.567。

对于C7采用折迭型突变模型有B3=(C7)1/2=0。

同理，对于B1、B2与B3采用“互补”燕尾型突变模型，有A1=average{(B1)1/2、(B2)1/3、(B3)1/4}=0.573，所以1号滑坡的总突变级数为0.573，属于中度危险。同理，其他滑坡总突变级数的计算结果见表7。由表可以看出，突变级数评价结果与现场调查结果基本吻合，准确率可达91%，证明该方法是可行的。虽然13、16号滑坡判别等级偏高于现场调查结果，但对于滑坡灾害防治而言，结果偏于安全，可提高防灾意识。并且突变级数法可以根据突变级数值将待评滑坡的危险性排序，为滑坡的防治提供依据。

5 结语

本文引入了一种新的滑坡危险性评价方法——突变级数法，该方法不仅减少了目前评价方法中由于权重确定带来的主观性，而且权衡了各层次评价指标的相对重要性。采用定性与定量相结合的方法，由归一化公式对目标进行评价与决策更为科学合理。

表7 研究区滑坡危险性评价结果Table 7 Evaluation results of landslide susceptibility degree in study area

为了使所选取的评价指标既全面又不重复，应注意分析评价指标间的相关性，本文应用皮尔逊积矩相关系数法求取了各评价指标间的相关系数，为计算突变级数时采用“互补”或“非互补”原则提供了依据，使得计算结果更为准确。

实例分析结果表明，基于突变级数法的滑坡危险性评价结果准确率高，而且可以根据突变级数值将待评滑坡的危险性排序，为滑坡的防治提供依据。

[1]乔建平，张小刚，林立相.长江上游滑坡危险度区划[J].水土保持学报，1994，8(1):39－44.QIAO Jian-ping，ZHANG Xiao-gang，LIN Li-xiang.Division of landslide danger degree on the upper reaches of the Yangtze River[J].Journal of Soil and Water Conservation，1994，8(1):39－44.

[2]唐川，周钜，朱静.云南崩塌滑坡危险度分区的模糊综合分析法[J].水土保持学报，1994，8(4):48－54.TANG Chuan，ZHOU Ju，ZHU Jing.The method of fuzzy comprehensive analysis of the risk zoning of rockfall and landslide in Yunnan[J].Journal of Soil and Water Conservation，1994，8(4):48－54.

[3]王成华，孔纪名.高速滑坡发生的危险斜坡判别[J].工程地质学报，2001，9(2):127－132.WANG Cheng-hua，KONG Ji-ming.The differentiating danger slope occurring high-speed landslide[J].Journal of Engineering Geology，2001，9(2):127－132.

[4]樊晓一，乔建平，陈永波.层次分析法在典型滑坡危险度评价中的应用[J].自然灾害学报，2004，13(1):72－76.FAN Xiao-yi，QIAO Jian-ping，CHEN Yong-bo.Application of analytic hierarchy process to assessment of typical landslide danger degree[J].Journal of Natural Disasters，2004，13(1):72－76.

[5]杨宗佶，乔建平.基于熵权的典型滑坡危险度评价[J].自然灾害学报，2009，18(4):31－36.YANG Zong-ji，QIAO Jian-ping.Entropy weight-based hazard degree assessment of typical landslide[J].Journal of Natural Disasters，2009，18(4):31－36.

[6]李军霞，王常明，王钢城.基于组合赋权-未确知测度理论的滑坡危险性评价[J].岩土力学，2013，34(2):468－474.LI Jun-xia，WANG Chang-ming，WANG Gang-cheng.Landslide risk assessment based on combination weighting-unascertained measure theory[J].Rock and Soil Mechanics，2013，34(2):468－474.

[7]梁桂兰，徐卫亚，何育智，等.突变级数法在边坡稳定综合评判中的应用[J].岩土力学，2008，29(7):1895－1899.LIANG Gui-lan，XU Wei-ya，HE Yu-zhi，et al.Application of catastrophe progression method to comprehensive evaluation of slope stability[J].Rock and Soil Mechanics，2008，29(7):1895－1899.

[8]安玉华，王清，张晨，等.基于突变模型的泥石流危险度评价[J].吉林大学学报(地球科学版)，2012，42(增刊1):355－361.AN Yu-hua，WANG Qing，ZHANG Chen，et al.Risk degree evaluation of debris flows based on catastrophic theory[J].Journal of Jilin University (Earth Science Edition)，2012，42(Supp.1):355－361.

[9]都兴富.突变理论在经济领域的应用[M].成都：电子科技大学出版社，1994.

[10]何平，赵子都.突变理论及其应用[M].大连：大连理工大学出版社，1989.

[11]乔建平，赵宇.滑坡危险度区划研究述评[J].山地学报，2001，19(2):157－160.QIAO Jiang-ping，ZHAO Yu.Review on risk degree regionalization of landslide[J].Journal of Mountain Science，2001，19(2):157－160.

[12]周福军.日冕水电站库区滑坡稳定性早期智能判别及危害模糊综合预测研究[博士学位论文D].长春:吉林大学，2013.

[13]梁飞豹，吕书龙，薛美玉，等.应用统计方法[M].北京：北京大学出版社，2010.

[14]VARNES D J.Landslide hazard zonation:a review of principles and practice[M].Paris:Unesco Press，1984.