基于GOCE卫星数据的重力场模型比较研究

郑增记 曹建平 范丽红 韩美涛

1)陕西省地震局，西安 710068

2)长安大学，西安710054

自2009年GOCE 卫星发射以来，基于GOCE 卫星重力数据，已经建立了多个高精度、高分辨率的静态地球重力场模型［1－8］。本文研究了近两年公布的基于GOCE 卫星数据的重力场模型的精度，比较了它们之间的差异，并分析了原因，为利用该重力场模型研究相关地球科学问题及利用GOCE 卫星数据进一步恢复地球重力场提供了科学依据。

1 评定重力场模型精度的方法

评定地球重力场模型本身的精度通常有两种方法:一种是比较重力场模型位系数误差的阶方差，另一种是比较重力场模型位系数差的阶方差。二者都可以以大地水准面高的形式表示［9－10］:

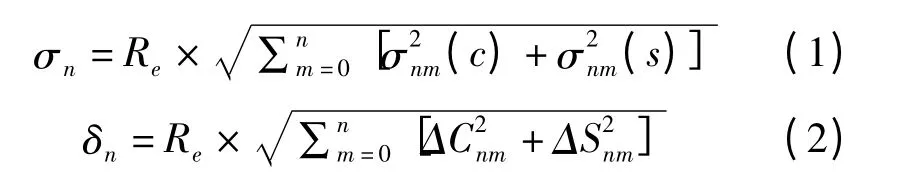
其中Re表示地球平均半径，σnm(c)、σnm(s)分别表示位系数Cnm、Snm的误差，ΔCnm、ΔSnm分别表示不同模型位系数之差。由式(1)、(2)，可以得到位系数误差的累计阶方差和位系数差的累计阶方差:

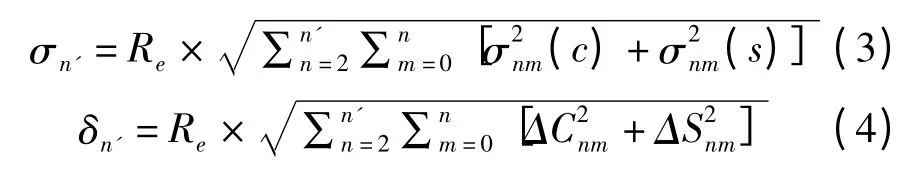
其中n'=n。

2 各模型比较分析

迄今为止，德国地学研究中心(GFZ)、德国波恩大学大地测量与地理信息研究所(IGG)、欧洲重力联合观测计划工作组(GOCO)和欧空局(ESA)等众多科研机构基于GOCE 卫星实测重力数据建立了多种高精度的地球重力场模型(表1)。表2、3 列出了本文所涉及的基于GOCE 卫星数据所建立的地球重力场模型的大地水准面起伏误差阶方差以及累计阶方差统计。为了比较，增加了EGM2008 模型和基于GRACE 卫星数据建立的ITG-GRACE2010S 模型。

2.1 基于单一卫星数据的重力场模型比较

图1、2 为GOCE-only 与卫星重力场模型大地水准面起伏误差的阶方差以及累计阶方差图。

从表2、3 和图1、2 可知:

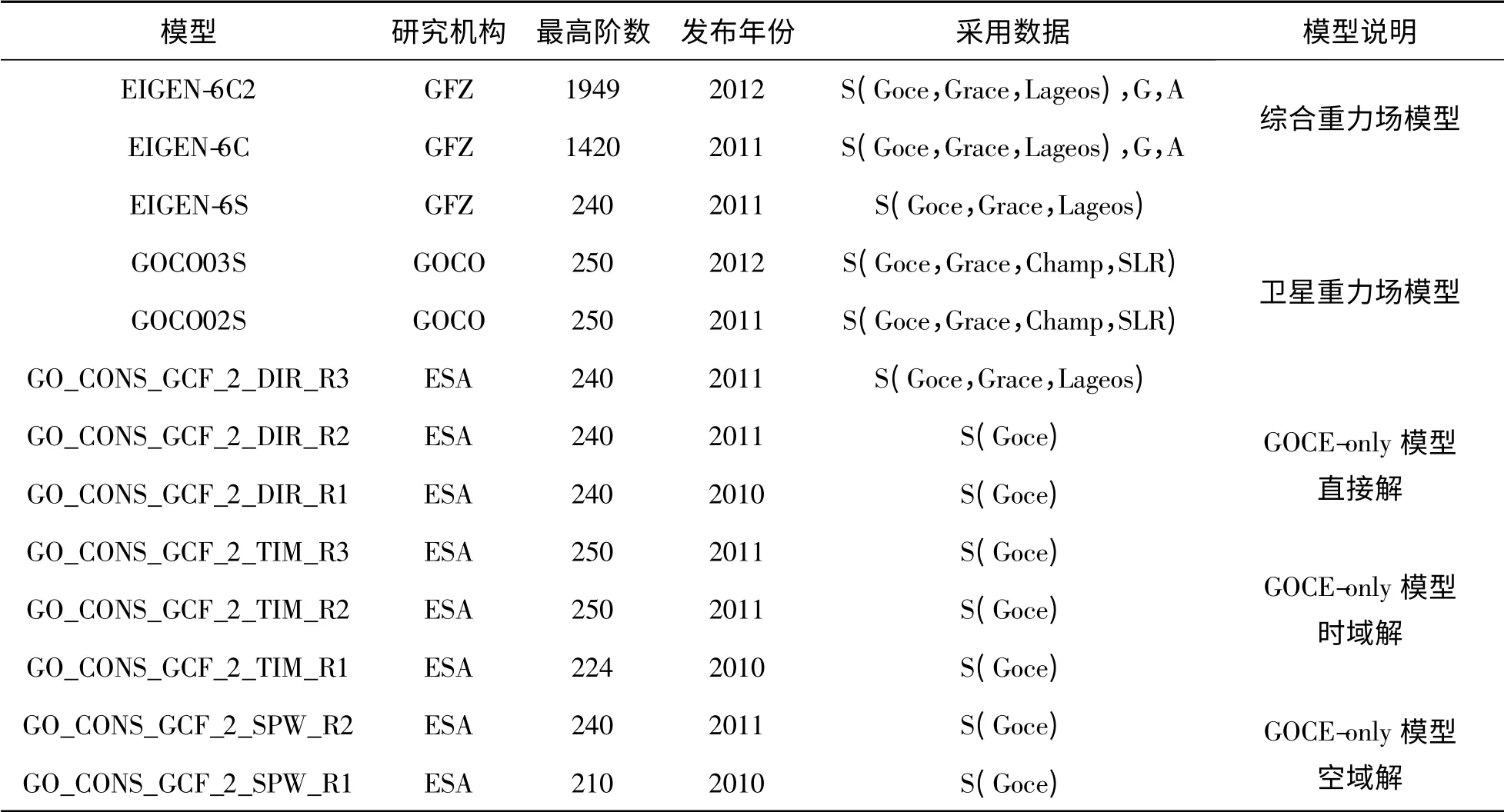
表1 基于GOCE 卫星数据重力场模型统计Tab.1 Statistics of gravity field models based on GOCE data

表2 各模型大地水准面起伏误差阶方差统计Tab.2 Statistics of geoid error degree variance of different models

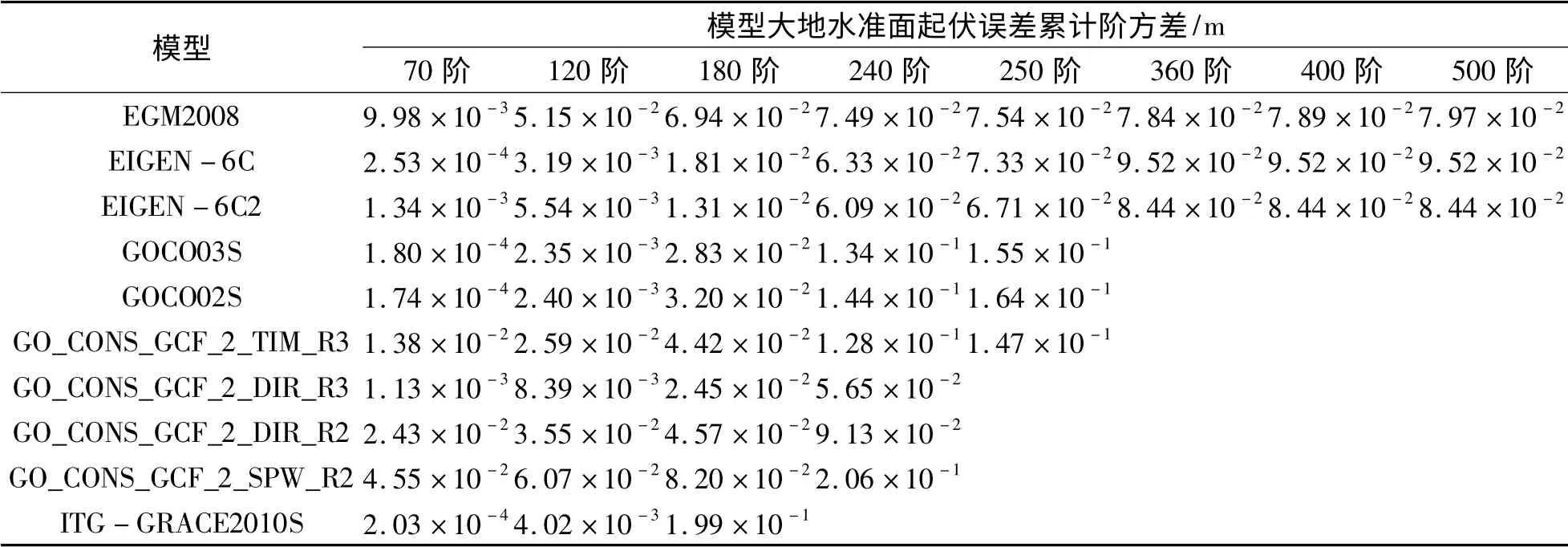
表3 各模型累计大地水准面精度统计Tab.3 Precision of accumulative geoid error degree variance of different models

图1 GOCE-only 模型与卫星重力场模型大地水准面起伏误差阶方差Fig.1 Geoid error degree variance of GOCE-only and satellite gravity models

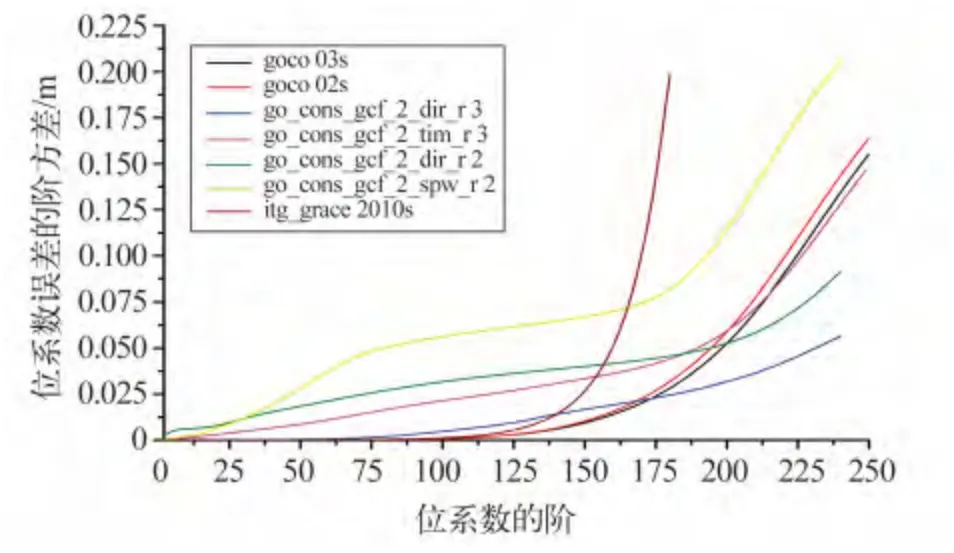
图2 GOCE-only 模型与卫星重力场模型大地水准面起伏误差累计阶方差Fig.2 Accumulative geoid error degree variance of GOCEonly and satellite gravity models

1)对于GOCE-only 重力场模型GO_CONS_GCF_2_TIM_R3、GO_CONS_ GCF_2_DIR_R2、GO_CONS_GCF_2_SPW-_R2 而言，解算方法不同，所得到的重力场模型的精度也不同。相对而言，GO_CONS_GCF_2_DIR_R2 模型精度最好，这是由于直接法［11］求解过程更加严密，并且解算中采用了精度更高的简化动力学轨道数据和先验重力场信息［12］;其次是时域法［13－15］解算的GO_CONS_GCF_2_TIM_R3 模型;精度最差的是空域法［16－18］解算的GO_CONS_GCF_2_SPW_R2 模型。

2)3 个GOCE-only 重力场模型在150 阶之后的大地水准面起伏误差阶方差为mm级，而GRACEonly 重力场模型ITG-GRACE2010S 为cm级，GOCE较GRACE 提高了一个数量级，这主要是由于GOCE重力卫星搭载的重力梯度仪可直接测定卫星轨道高度处引力位的二阶导数，将球谐系数放大了12 倍，可有效抑制地球引力位随高度的衰减效应，更高精度地感测中长波重力场。

3)目前，利用GOCE 卫星数据恢复重力场模型的最高能力为250 阶，GO_CONS_GCF_2_TIM_R3模型在250 阶处的累计大地水准面精度为14.7 cm。

4)GO_CONS_GCF_2_DIR_R3 虽然也是直接解，但由图2 可知，其精度优于GO_CONS_GCF_2_DIR_R2，这是由于该模型不仅采用了GOCE 卫星重力数据，而且采用了GRACE 卫星和LAGEOS 卫星重力数据，这说明综合各种卫星数据有利于进一步提高重力场模型中长波信息的精度。

2.2 基于多种卫星数据的重力场模型比较

由表2、3 和图1、2 可知:

1)虽然GOCO03S 与GOCO02S 模型所采用的数据种类、解算方法完全相同，但GOCO03S 较GOCO02S 精度高，这是由于GOCO03S 比GOCO02S 采用的GOCE 卫星数据多出10 个月，适当增加卫星重力数据的观测时间有利于提高重力场恢复的精度。

2)在前180 阶，GO_CONS_GCF_2_D-IR_R3 模型与GOCO03S、GOCO02S 模型精度相当，但180 阶之后，GO_CONS_GCF_2-_DIR_R3 模型精度较高，这可能与GOCO03S、GOCO02S 模型从180 阶开始进行Kaula 正则化有关。从图1、2 及表3 可以看出，卫星重力场模型GOCO03S、GOCO02S 在前240阶与GOCE-only 重力场模型模型GO_CONS_GCF_2_TIM_R3、GO_CONS_GCF_2_DIR_R2 精度相当。由此可得出，GOCE 卫星在探测地球中长波信息方面精度较高，由其重力数据得出的重力场模型有时可以与综合利用GRACE/CHAMP/SLR 等卫星数据得出的重力场模型相媲美。

由于在上述卫星重力场模型中，GO_CONS_GCF_2_DIR_R3 精度最高，故将其与综合重力场模型进行比较，见图3、4。

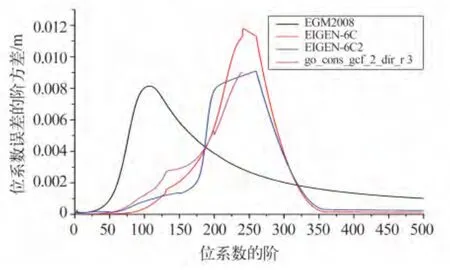
图3 GO_CONS_GCF_2_DIR_R3 与综合重力场模型大地水准面起伏误差阶方差Fig.3 Geoid error degree variance of GO_CONS_GCF_2_DIR_R3 and comprehe-nsive gravity models

3)从表2 和图3、4 看出，GO_CONS_GCF_2_DIR_R3 模型大地水准面起伏误差的阶方差在180阶之前低于EGM2008 模型，而大地水准面起伏误差的累计阶方差在240 阶之前要优于EGM2008 模型。这是因为EGM2008 模型在低阶部分采用了GRACE数据，而GO_CONS_GCF_2_DIR_R3 模型主要基于GOCE 卫星数据解算而得。另外，综合重力场模型EIGEN-6C、EIGEN-6C2 在这一低阶部分比EGM2008 模型精度高同样是由于这方面的原因。

4)从图4 可知，模型大地水准面起伏误差累计阶方差在120 阶以内较为平缓，120 阶之后急剧上升，250 阶以后又平缓变化。原因是:在低阶位系数部分，EGM2008 模型主要采用GRACE 卫星的中长波信息计算而得，EIGEN-6C、EIGEN-6C2 模型主要采用GOCE 卫星中长波信息。此外在高阶部分这3个模型主要采用地面重力数据，精度较高，反映在图像上是120 阶之前和250 阶之后较为平缓;120 ～250 阶之间急剧上升，可能是由于在确定地球重力场模型时采用不同方法(如Kaula 正则、Tikhonov 正则)使奇异阵可求逆导致的［19－20］。

2.3 综合重力场模型比较分析

图5、6 为EIGEN-6C、EIGEN-6C2 与EGM2008位系数差的大地水准面起伏阶方差及累计阶方差图。从表2、3 和图5、6 可知:

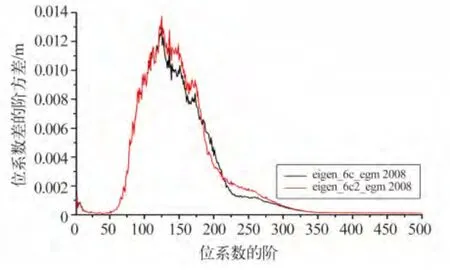
图5 综合重力场模型位系数差的大地水准面起伏阶方差Fig.5 Geoid degree variances of potential coefficient difference between EGM2008 and EIGEN-6-C，EIGEN-6C2

图6 综合重力场模型位系数差的累计大地水准面起伏阶方差Fig.6 Accumulative geoid degree variance of potential coefficient difference between EGM2008 and EIGEN-6C，EIGEN-6C2

1)EIGEN-6C、EIGEN-6C2 与EGM2008 模型位系数差的大地水准面起伏阶方差在125 阶时达到最大值，分别为1.30、1.37 cm，350 阶之后相差较小，其中350 阶时分别为0.162、0.171 mm。

2)EIGEN-6C、EIGEN-6C2 与EGM2008 模型位系数差的累计大地水准面起伏阶方差在200 阶之后趋于稳定，大致为0.101、0.105 m。

3 结 论

1)相较于GRACE 卫星，GOCE 重力卫星所获得的重力场信息更为丰富，也更为精确，并且在150 阶之后，GOCE 较GRACE 提高了一个数量级。

2)在利用相同卫星重力数据恢复地球重力场时，解算方法不同得到的重力场模型精度也不同，其中直接法精度最高，时域法次之，空域法最差。

3)目前，GOCE 卫星恢复地球重力场模型的最大能力为250 阶次，在250 阶处的累计大地水准面精度约为14.7 cm。

4)EIGEN-6C、EIGEN-6C2 与EGM2008 模型位系数差的累计大地水准面起伏阶方差在200 阶之后大致为0.1 m。

致谢感谢欧空局(ESA)、德国地学研究中心(GFZ)、德国波恩大学大地测量与地理信息研究所(IGG)及欧洲重力联合观测计划工作组( GOCO)提供本文计算所需的重力场模型数据!

1 许厚泽.卫星重力研究:21世纪大地测量研究的新热点［J］.测绘科学，2001，26(3):1－3.(Xu Houze.Satellite gravity missions-new hotpoint in geodesy［J］.Science of Surveying and Mapping，2001，26(3):1－3)

2 许厚泽，周旭华，彭碧波.卫星重力测量［J］.地理空间信息，2005，3(1):1－3.(Xu Houze，Zhou Xuhua，Peng Bibo.Satellite gravity measurement［J］.Geospatial Information，2005，3(1):1－3)

3 Simons M，Hager B H.Localization of the gravity field and the signature of glacial rebound［J］.Nature，1997，390(6659).

4 Zhong M，Naito I，Kitoh A.Atmospheric，hydrological and ocean current contributions to Earth’s annual wobble and length-of-day signals based on output from a climate model［J］.Journal of Geophysical Research，2003，108(B1).

5 Tapley B D，Bettadpur S，Ries J C，et al.GRACE measurements of mass variability in the Earth system［J］.Science，2004，305(5 683).

6 Han S C，Shum C K，Bevis M，et al.Crustal dilatation observed by GRACE after the 2004 Sumatra–Andaman earthquake［J］.Science，2006，313(5 787).

7 Pollitz F F.A new class of earthquake observations［J］.Science，2006，313(5 787).

8 Chen J L，Wilson C R，Tapley B D.Satellite gravity measurements confirm accelerated melting of the Green-landice sheet［J］.Science，2006，313(5 795):1958－60.

9 周旭华，吴斌，彭碧波，等.利用CHAMP 科学轨道数据和星载加速度计数据反演地球重力场［J］.武汉大学学报:信息科学版，2006，31(2):172－175.(Zhou Xuhua，Wu Bin，Peng Bibo，et al.Earth’s gravity field recovered from CHAMP science orbit and accelerom-eter data［J］.Geomatics and Information Science of Wuhan University，2006，31(2):172－175)

10 周旭华，许厚泽，吴斌，等.用GRACE 卫星跟踪数据反演地球重力场［J］.地球物理学报，2006，49(3):715－723.(Zhou Xuhua，Xu Houze，Wu Bin，et al.Earth’s gravity field derived from GRACE satellite tracking data［J］.Chinese Journal of Geophysics，2006，49(3):715－723)

11 Bruinsma S L，Marty J C，Balmino G，et al.GOCE gravity field recovery by means of the direct numerical method［C］.The ESA Living Planet Symposium，Bergen，2010.

12 Pail R，Bruinsma S，Migliaccio F，et al，First GOCE gravity field models derived by three different approaches［J］.Journal of Geodesy，2011，85(11):819－843.

13 Reguzzoni M.From the time-wise to space-wise GOCE observables［J］.Adva-nces in Geo-sciences，2003(1).

14 Sneeuw N.Space-wise，time-wise，torus and rosborough representations in gravity field modeling［J］.Space Science Revie-ws，2003，108(1).

15 Pail R，Goiginger H，Mayrhofer R，et al.GOCE gravity field model derived from orbit and gradiometry data applying the time-wise method［C］.The ESA Living Planet Symposium，Bergen，2010.

16 Migliaccio F，Reguzzoni M，Sanso F.Space-wise approach to satellite gravity field deter mination in the presence of coloured noise［J］.Journal of Geodesy，2004，78(4).

17 Reguzzoni M，Tselfes N.Optimal multi-step collcation:applicaltion to the space-wise approach for GOCE data analysis［J］.Journal of Geodesy，2009，83(1):13－29.

18 徐天河，贺凯飞，吴显兵.CHAMP 重力场恢复时域法和空域法比较研究［J］.地球物理学进展，2009，24(2):456－461.(Xu Tianhe，He Kaifei，Wu Xianbing.Comparison of time-wise approach and space-wise approach for CHAMP gravity field recovery［J］.Progress in Geophysics，2009，24(2):456－461)

19 罗佳，姜卫平，汪海洪，等.中国区域SST 卫星重力场模型精度分析［J］.武汉大学学报:信息科学版，2006，31(3):199－202.(Luo Jia，Jiang Weiping，Wang Honghai，et al.Precision analysis of SST gravity field model in China［J］.Geomatics and Information Science of Wuhan University，2006，31(3):199－202)

20 宁津生，王正涛.地球重力场研究现状与进展［J］.测绘地理信息，2013，38(1):1－7.(Ning Jinsheng，Wang Zhengtao.Prograss and present status of research on earth’s gravitational field［J］.Journal of Geomatics，2013，38(1):1－7)