时序干涉测量中大气垂直分层延迟校正研究

顾兆芹 宫辉力 张有全 杜钊锋 刘欢欢 王 洒 卢学辉

1)首都师范大学三维信息获取与应用教育部重点实验室，北京 100048

2)中国科学院成都山地灾害与环境研究所，成都610041

合成孔径雷达干涉测量中的大气延迟误差主要由电离层离散效应和对流层折射效应引起［1－2］。电离层引起的相位延迟在高纬度地区或长波长(L 波段)图像［3－4］中比较明显，而当图像尺度＞100 km［1－2］时，亦不容忽视;对流层引起的相位延迟在几km 至几十km 的图像中显著［1］。

在量化和缓解大气垂直分层延迟方面，国内外学者开展了大量工作:一类是基于各误差组分信号的时空分布及变化特征进行评估，主要是基于相位延迟模式的统计特性［6］，构建协方差矩阵，用以从干涉相位中分离随机噪声信号。此外，由于大气延迟信号在时间尺度上不相关［7］，采用相位累积方法［8］、时域低通滤波方法或永久散射体技术(PS-In-SAR)和小基线技术(SB-InSAR)所采用的时间-空间滤波方法［9－11］都可有效地抑制形变相位的噪声。这3 种方法适用于地表形变速率变化相对平缓的地区，但应用受SAR 数据采样密度及大气垂直延迟的影响。其他方法包括直接分析InSAR 干涉相位与高程关系，评估大气垂直分层延迟［12］;或者借助外部数据，例如气象监测站数据，利用大气折射计算公式［2］评估大气垂直分层延迟组分，并进行空间插值［13］，但易受近地表强边界效应尤其是湿度的影响。MODIS［14］、MERIS［15－17］或者高密度的GPS 网数据［18－19］已经成功应用于地表到卫星的水汽制图，可获取非均质各向异性的水汽变化特性，但这些外部数据的主要限制因素是:GPS 监测站空间分布密度低，SAR 影像与MODIS 数据获取时间不同步，MODIS 和MERIS 易受数据校正、云层的影响。中尺度大气动力学气象模型可评估区域天顶静力学延迟、天顶湿延迟［20－23］，但由于天气预测能力低和模型边界条件比较敏感等，应用受到限制。

本文在识别研究区大气垂直分层延迟幅度及特征的基础上，采用多尺度分解方法评估高程-相位比例系数及最佳分解尺度，校正Las Vegas 地区时序干涉测量结果中的大气垂直分层延迟，从而验证了该方法的有效性。

1 多尺度分解方法

1.1 高程-相位关系

SAR 干涉测量中，大气延迟可分解为大气垂直分层延迟和水平紊乱延迟两部分［5］。相对于水平紊乱延迟随机分布引起的不确定性，大气垂直分层延迟在一定时间段及区域内是相对稳定的［3，5，24］。重复轨道干涉测量中，相邻干涉图中的大气垂直分层延迟幅度不同。将干涉相位按照泰勒级数展开至一次项，忽略高次项影响，可获取高程与干涉相位的关系:

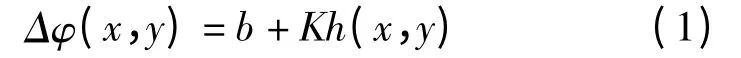
其中，Δφ(x，y)为干涉相位，h(x，y)为坐标(x，y)处高程，K 为高程-相位比例系数，b 为常数。该高程-相位的线性模型建立在最小二乘拟合的基础上，适用于常规天气、中低纬度地区。采用全景干涉图而不是全局分块方式评估高程-相位比例系数，可以更好地考虑形变区影响［24］，此时的高程-相位比例系数在干涉图中具有全局特性及唯一性。简单的线性回归评估高程-相位关系易引起误差传递，因此需要更可靠的方法评估高程-相位比例系数。

1.2 永久散射体技术中多尺度分解校正方法

干涉相位中各误差组分在不同图像尺度(L)上敏感性不同。例如，当图像尺度L ＞100 km 时，轨道误差影响在干涉测量中误差不容忽视［1，25］;而L 小于2 km 时，大气延迟影响则较小可以忽略［3］。也有研究表明，若地形高程差Δh ＞500 m，大气垂直分层延迟有时可以达到1 cm［5］。因此，由图像尺度L 确定合适的高程-相位比例系数K，有助于更好地校正大气垂直分层延迟误差。

假设图像尺度空间L(x，y，λ)定义为原始图像I(x，y)与一个可变尺度的2 维高斯函数G(x，y，λ)卷积运算［26］:

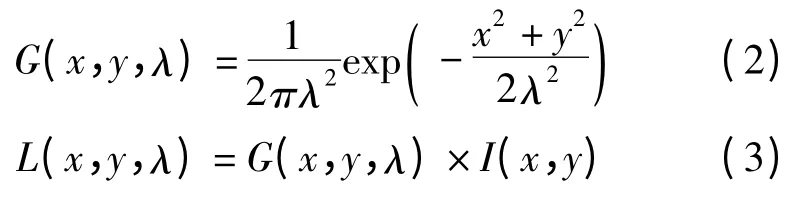
其中，λ 为图像分解尺度，是可变的。多尺度变换中图像分解尺度依次取值(λ，kλ，k2λ…kn－1λ)，本次研究中令k=2，代表相邻图像尺度为2 倍关系。

将DEM、时序干涉测量结果(相干点)在多尺度(λ，kλ，k2λ，…，kn－1λ)进行分解，即高斯滤波，可得到低通、高通滤波图像。在此基础上，获取带通滤波图像B(x，y，λ):

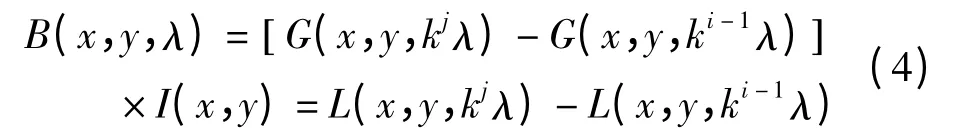
此时，大气垂直分层延迟模型可进一步表示为:

其中，Δφigram为第i 次低通、高通滤波后的干涉图像，ΔφBgram为第i 次带通滤波后的干涉图像，x、y 代表低通、带通、高通滤波图像中相干点的坐标，i 取值0，1，2…n－1。

对m 景SAR 影像干涉图进行n 次高斯滤波(低通滤波、高通滤波)、高斯差分滤波(带通滤波)，利用干涉相位构建协方差矩阵，统计分析高程-相位比例系数Kmn，见公式(6)，其中，bmn、Kmn、hm(x，y，λn)、Δφm(x，y，λn)分别代表第m 景影像第n 次滤波后干涉图像中常数、高程-相位比例系数、高程、干涉相位，结合高程-相位的最大相关系数Rmn(公式为第m 景影像第n 次滤波后x、y 坐标的算术平均值，j 为第m 景影像第n 次滤波后图像中的永久散射体点)确定最佳高程-相位比例系数K，评估m 景干涉图中大气垂直分层延迟量，进而从干涉相位中校正缓解大气垂直分层延迟:

2 数据选取与大气垂直分层延迟识别

2.1 研究区及数据处理

研究区选择美国拉斯维加斯地区，覆盖面积为80 km×80 km(图1)。SAR 数据采用Envisat 卫星C 波段降轨单视复图像(SLC)，获取时间为2002-10～2009-10;外部DEM 采用美国宇航局(NASA)和国防部国家测绘局(NIMA)提供的1 s SRTM 高程数据;轨道数据采用2002 ～2010年的CEOS 精密轨道数据文件;差分干涉处理采用Doris 软件;永久散射体干涉处理采用StamPS 软件。

选取影像时考虑了时空基线最优原则［27］:1)垂直基线B⊥＜500 m;2)时间基线T ＜5 a;3)多普勒质心频率Fdc＜300 Hz;4)季节相干性＞0.5。分析4 个因子相干性影响，摒弃相干性低的影像，共选取27 景图像(表1)。相干性最高的2007-11-23 的SAR 影像为最佳公共主图像，进行永久散射体干涉处理，共识别了48 万个相干点。

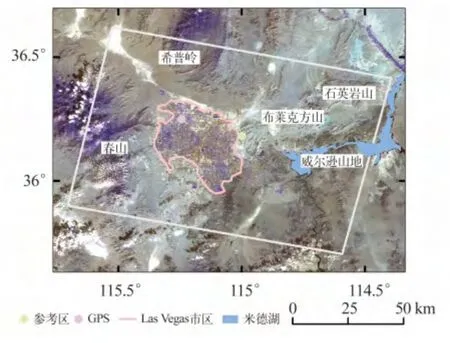
图1 研究区位置Fig.1 Location map of Las Vegas

表1 SAR 影像干涉参数Tab.1 Parameters of INSAR data

2.2 大气延迟组分识别与分析

为了更好地了解拉斯维加斯地区大气延迟特征，根据气象监测站点2002 ～2010年的监测数据(温度T，压强P，海拔H，湿度W)，利用北美大气模型NARR 计算拉斯维加斯地区海拔748 m 处气象点(114.957°W，36.319°N)300 ～2 400 m 压力面处大气延迟［2］，进而统计分析大气延迟各组分的幅度、周期及季节性变化规律(图2)。

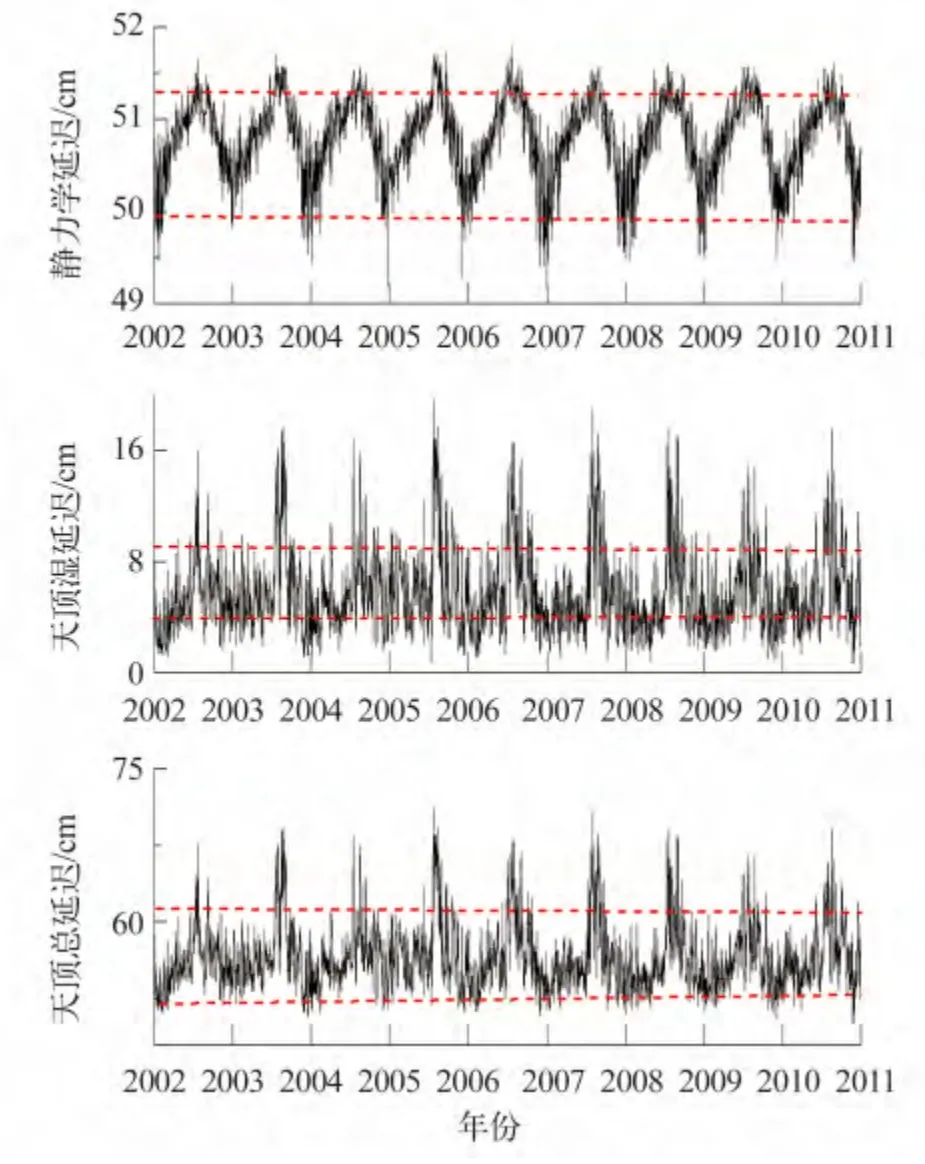
图2 NARR 气象模型大气延迟分析图Fig.2 Single path propagation delay computed using NARR

对流层中的大气延迟(天顶总延迟)主要由两部分组成:静力学延迟和天顶湿延迟［28］。静力学延迟主要受近地表压强P、湿度W、温度T 影响，其年际变化曲线呈现很好的周期性，波动幅度约为1.8 cm，该变化量大于该地区形变的幅度，在InSAR 形变结果中不容忽视［24］。天顶湿延迟主要受近地表湿度W 的影响，短期平均波动幅度约为9 cm，同时季节性波动幅度约为4.1 cm，最大延迟发生在7 ～10月季风季节，最小延迟在1 ～3月。统计研究区天顶总延迟，发现部分静力学延迟和天顶湿延迟相互抵消。天顶总延迟波动幅度约为6 cm，季节性波动主要受天顶湿延迟影响。最小延迟在1月，最大延迟在8月。

InSAR 干涉测量中通常将大气延迟分解为大气垂直分层延迟和水平紊乱延迟。其中，大气垂直分层延迟主要由静力学延迟组成，同时小部分天顶湿延迟也有贡献;水平紊乱延迟则主要由天顶湿延迟组成。水平紊乱延迟在时间上呈现随机性特征，在SAR 影像不足的情况下，不能简单地采用相位累积方法去除，以免滤去部分形变。大气垂直分层延迟与地形有较强的相关性，受限于数据收集量，本文只校正大气垂直分层延迟。

本次工作曾尝试采用大气模型方法校正研究区内的大气垂直分层延迟，但结果不理想。分析其原因，可能是大气模型的空间分辨率太低(北美大气模型网格分辨率为32 km)，但大气模型结果可以辅助分析拉斯维加斯地区的大气延迟各组分及特征。

3 校正结果及分析

依据大气模型统计的拉斯维加斯地区大气延迟特点，采用§1.1 高程-相位模型与§1.2 多尺度分解方法，将干涉图、DEM(高程)进行多尺度分解，初始分解尺度为1.6 km，分解尺度从低频到高频为＞25.6 km、12.8 ～25.6 km、6.4 ～12.8 km、3.2 ～6.4 km、1.6 ～3.2 km、＜1.6 km，分离长波长信号中的大气垂直分层延迟信号。共获取多尺度分解干涉图156 景，高程-相位比例系数K 值156 个。由于大气垂直分层延迟具有长波长特征及全局特性，易受波长相对较长的形变信息干扰，故采用形变区外的相干点评估高程-相位比例系数。

利用干涉图自身数据评估高程-相位比例系数的误差来源主要有:1)残余轨道或地形误差;2)大气垂直分层延迟;3)水平紊乱延迟。InSAR 数据集的选取及研究区内的地形都会影响干涉图的主要误差。选取影像2009-07-10、2002-11-29、2009-06-05影像与公共主图像2007-11-23 干涉结果图，其主要误差分别为大气垂直分层延迟、轨道误差、水平紊乱延迟，统计高程-相位相关性及比例系数，见图3。

从图3 可以看出，相对于低通、高通滤波图像，带通滤波图像的高程-相位相关性R 更大，线性关系更明显，因此选择带通滤波图像统计的高程-相位比例系数校正研究区大气垂直分层延迟。根据相关性影响，确定研究区高斯多尺度分解的最佳尺度为12.8 ～25.6 km，进而获取26 景干涉图最佳高程-相位比例系数K 值(图4)。高程-相位的相关性越大，干涉图中大气垂直分层延迟越明显;相关性越小，大气垂直分层延迟越不明显，干涉图越有可能叠加水平紊乱延迟或轨道误差信息。

依据地形-相位比例系数最佳K 值(图4)，对2002-10 ～2009-10 拉斯维加斯地区大气垂直分层延迟进行校正，进而提取该区域年平均形变速率图(图5(a)、(c)，红色表示沉降，蓝色表示上升)和大气延迟图(图5(b))。

图3 多尺度分解后干涉图中高程-相位散点图Fig.3 Scatter plots between phase and elevation after corrected by multi-scale technology

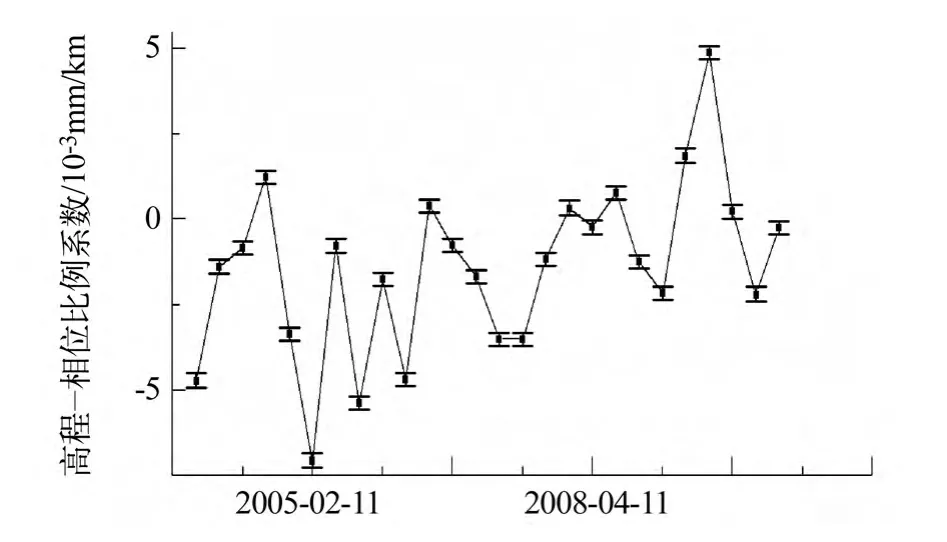
图4 高程-相位比例系数K 值Fig.4 Proportional coefficient K between phase and elevation

1)由于过去持续过量开采地下水，拉斯维加斯市区地表形变信息明显，城市中心明显形成1个上升漏斗，2 个下降漏斗(5(a))。1 ～6 区属于山区，这些地区几乎没有形变。由于大气垂直分层延迟的影响，年平均形变速率图中出现不同程度的“形变”信息，分析主要为大气垂直分层延迟信息。对比图1、3，这些延迟信息与地形即高程具有一定的相关性，高程越大，大气垂直分层延迟越明显，延迟幅度越大。

2)大气延迟幅度在整个研究区内是不同的(图5(b))，根据§2.2 大气延迟组分的识别与分析，利用北美大气模型统计，该区大气延迟波动幅度约为6 cm，经永久散射体干涉处理后，干涉图中的大气延迟幅度约为－0.7 ～2 rad(－9 ～3.2 mm)，相对于该区域地表形变每年约为－4.2 ～5.7 mm，大气延迟幅度达到形变幅度，容易被误解为形变信息。

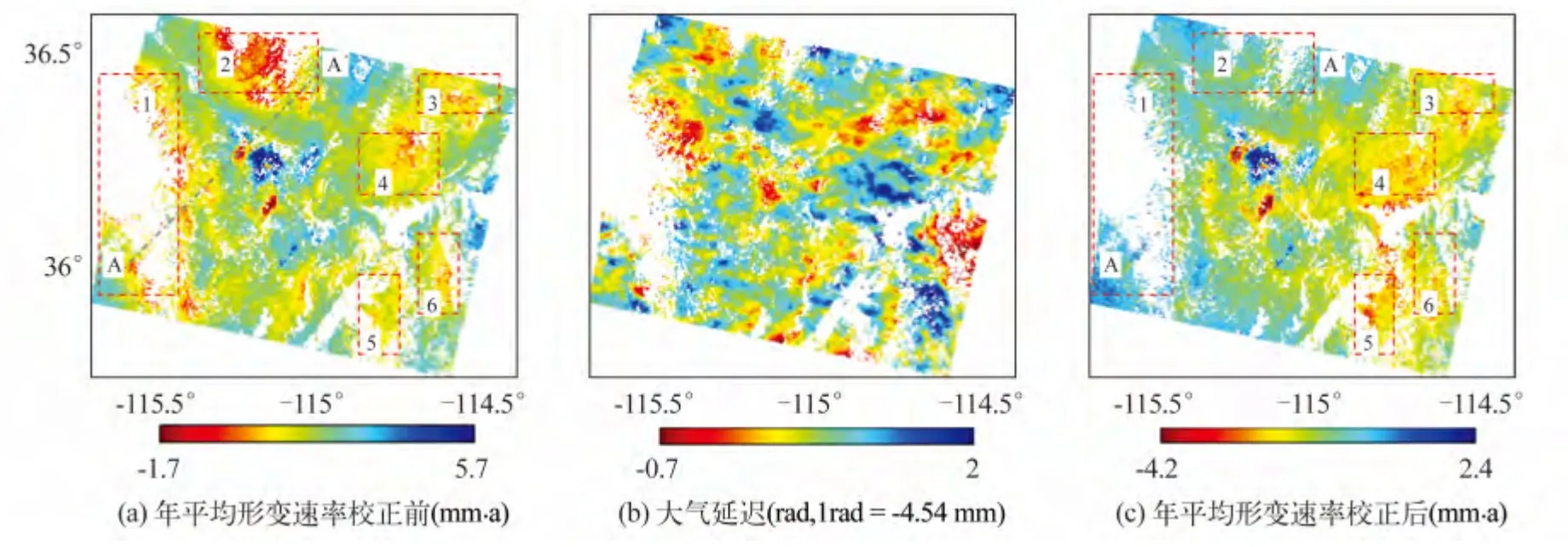
图5 拉斯维加斯地区2002 ～2009年地表形变速率大气垂直分层延迟校正效果(高斯多尺度技术)Fig.5 Deformation rate during 2002 to 2009 in Las Vegas before and after correcting

3)采用高斯多尺度分解方法校正后的年平均速率图中(图5(c))，在1、2 区，大气垂直分层延迟得到成功缓解，年平均形变速率从－1.6 ～0.1 mm/a 降为－0.2 ～0.1 mm/a;A－A'线段穿越了1 区、下降漏斗、2 区，其校正前后形变速率如图6，校正后的山区及其他非形变区域形变量均在0 值上下波动，形变速率波动较大地区为沉降漏斗区。

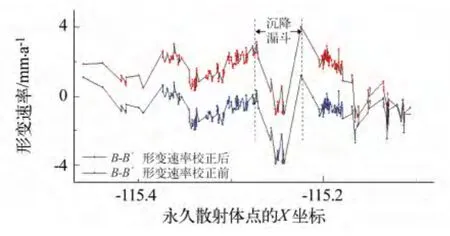
图6 形变速率校正前后结果对比Fig.6 Comparison rate of deformation before and after correction

校正后研究区内大气垂直分层延迟有一定减弱，但仍存在部分残余信息，如图5 中3 ～6 区。从图5 中可以看出，3 区校正效果不理想，在InSAR 干涉测量中形变速率校正后从－0.3 ～1.3mm/a 变为－2 ～－1.2mm/a，校正前后的形变速率图中，干涉测量结果均未显示真实的形变信息。这可能与高程相位比例系数评估方式有关，在这个地区需要考虑局部分区方法评估大气垂直分层延迟。4 区位于米德湖北方，即Black Mesa 山区，形变速率从－0.5 ～0.8mm/a 变为－1.2 ～2.4mm/a，由于在1992 ～2002年米徳湖区域形变约为－11.5 ～3mm，其形变速率约为－1.15 ～0.3mm/a［24］，由此推断校正后相位信息主要包括两个部分:一部分是形变信息，受米徳湖蓄水、载荷的影响，该区岩层呈现回弹、下降变化趋势;另一部分是水平紊乱延迟信息，从大气延迟图5(b)中可以看出，大气延迟幅度可达9 mm 左右，校正后除了真实的形变信息外，可能存在残余的大气垂直分层延迟，同时水平紊乱延迟幅度亦不容忽视。5 区位于新的开采水源地，超量开采地下水可能导致新的沉降区域，该区相位信息需要进一步核实。6 区校正前后都未显示真实的形变信息，对比图1 发现，该区位于米徳湖泄水区域，同时图5(b)中大气延迟幅度约为6.2 ～8.0 mm，推测误差主要为水平紊乱延迟误差。

对比图5(a)、(c)发现，左侧山区大气垂直分层延迟成功缓解，而右侧米徳湖周边地区校正效果不理想，分析其原因为水平紊乱延迟影响。可见，多尺度分解方法评估大气垂直分层延迟适用于干旱少雨地区，对于复杂气候地区，则需要一种更合适的方法。

4 结 论

1)将多尺度分解方法成功应用到美国Las Vegas 地区，大气垂直分层延迟校正后年平均形变速率从－1.6 ～0.1mm/a 降为－0.2 ～0.1mm/a;同时发现，在气象条件变化剧烈、地形复杂地区，需要采用局部分区方法评估高程-相位比例系数。

2)多尺度分解方法可以有效缓解干涉测量中的大气垂直分层延迟，提高干涉测量精度。但需注意，若研究区中有明显复杂的水平紊乱延迟，多尺度分解方法校正大气垂直分层延迟将受到一定的限制，需要考虑其他方法去除水平紊乱延迟。

3)针对大气垂直分层延迟校正中出现的误差，文中给予了合理解释。采用线性模型可能过低评估永久散射体干涉测量中的大气垂直分层延迟，下一步将开展非线性模型、指数模型评估大气延迟。

致谢感谢弗吉尼亚理工大学Thomas J Burbey 博士提供的合作研究机会; 感谢荷兰Delft 理工大学Hopper 博士提供的StamPS 干涉测量软件及美国宇航局( NASA)提供轨道星历。

1 Hooper A，Bekaert D，Spaans K，et al.Recent advances in SAR interferometry time series analysis for measuring crustal deformation［J］.Tectonophysics，2012，514－517:1－13.

2 Doin M P，Lasserre C，Peltzer G，et al.Corrections of stratified tropospheric delays in SAR interferometry:Validation with global atmospheric models［J］.Journal of Applied Geophysics，2009，69(1):35－50.

3 Lin Y N，Simons M，Hetland E A，et al.A multiscale approach to estimating topographically correlated propagation delays in radar interferograms［J］.Geochemistry Geophysics Geosystems，2010，11(9):1－17.

4 Gray A L，Mattar K E，Sofko G.Influence of ionospheric electron density fluctuations on satellite radar interferometry［J］.Geophys Res Lett，2000，27(10):1 451－1 454.

5 Hanssen R F.Radar interferometry:data interpretation and error analysis［M］.Dordrecht:Kluwer Academic Publishers，2001.

6 Lohman R B，Simons M.Some thoughts on the use of InSAR data to constrain models of surface deformation:Noise structure and data downsampling［J］.Geochemistry Geophysics Geosystems，2005，6(1):1－12.

7 Zebker H A，Rosen P A，Hensley S.Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps［J］.Journal of Geophysical Research，1997，102(B4):7 547－7 563.

8 Schmidt D A.Distribution of aseismic slip rate on the Hayward fault inferred from seismic and geodetic data［J］.Journal of Geophysical Research，2005，110(B8):1－15.

9 Ferretti A P C，Rocca F.Permanent scatterers in SAR interferometry［J］.IEEE Transactions on Geoscience and Remote Sensing，2001，39(1):8－20.

10 Berardino P，Fornaro G，Lanari R，et al.A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms［J］.IEEE Transactions on Geoscience and Remote Sensing，2002，11(40):2 375－2 383.

11 Hooper A S P，Zebker H.Persistent Scatterer interferometric synthetic aperture radar for crustal deformation analysis，with application to volcan Alcedo，Galapagos［J］.Journal of Geophysical Research，2007，112(B7):1－21.

12 Elliott J R，Biggs J，Parsons B，et al.InSAR slip rate determination on the Altyn Tagh fault，northern Tibet，in the presence of topographically correlated atmospheric delays［J］.Geophys Res Lett，2008，35(L12309).

13 Delacourt C，Briole P，Achache J A.Tropospheric corrections of SAR interferograms with strong topography application to Etna［J］.Geophysical Research Letters，1998，25(15):2 849－2 852.

14 宋小刚，李德仁，单新建，等.基于GPS 和MODIS 的ENVISAT ASAR 数据干涉测量中大气改正方法研究［J］.地球物理学报，2009，52(6):1 457－1 464.(Song Xiaogang，Li Deren，Shan Xinjian，et al.Correction of atmospheric effect in ASAR interferogram using GPS and MODIS data［J］.Chinese Journal of Geophysics，2009，52(6):1 457－1 464)

15 许文斌，李志伟，丁晓利，等.利用MERIS 水汽数据改正ASAR 干涉图中的大气影响［J］.地球物理学报，2010，53(5):1 073－1 084.(Xu Wenbin，Li Zhiwei，Ding Xiaoli，et al.Correcting atmospheric effects in ASAR interferogram with MERIS integrated water vapor data［J］.Chinese Journal of Geophysics，2010，53(5):1 073－1 084)

16 Li Z，Fielding E J，Cross P，et al.Interferometric synthetic aperture radar atmospheric correction:medium resolution imaging spectrometer and advanced synthetic aperture radar integration［J］.Geophys Res Lett，2006，33.

17 Li Z，Muller J，Cross P，et al.Assessment of the potential of meris near-infrared water vapour products to correct ASAR interferometric measurements［J］.International Journal of Remote Sensing，2006，33.

18 Li Z，Fielding E J，Cross P，et al.Interferometric synthetic aperture radar atmospheric correction:GPS topography-dependent turbulence model［J］.J Geophys Res，2006，111:B02404.

19 常亮.基于GPS 和美国环境预报中心观测信息的InSAR大气延迟改正方法研究［J］.测绘学报，2011，40(5):1 001.(Chang Liang.InSAR atmospheric delay correction based on GPS observations and NCEP data［J］.Acta Geodaetica et Cartographica Sinica，2011，40(5):1 001)

20 Wadge G.Atmospheric models:GPS and InSAR measurements of the tropospheric water vapour field over mount Etna［J］.Geophysical Research Letters，2002，29(19).

21 林乐科，张业荣，赵振维，等.基于天顶湿延迟的GPS 大气折射率剖面反演研究［J］.全球定位系统，2007，32(3):1－4.(Lin Leke，Zhang Yerong，Zhao Zhenwei，et al.Study on retrieving atmosphere refractivity profiles using zenith wet delay(ZWD)of GPS［J］.GNSS World of China，2007，32(3):1－4)

22 Puyssegur B，Michel R，Avouac J P.Tropospheric phase delay in interferometric synthetic apertur radar estimated from meteorological model and multispectral imagery［J］.J Geophys Res，2007，112(B05419).

23 Foster J，Brooks B，Cherubini T，et al.Mitigating atmospheric noise for InSAR using a high resolution weather model［J］.Geophys Res Lett，2006，33(L16304).

24 Cavalié O，Doin M P，Lasserre C，et al.Ground motion measurement in the Lake Mead area，Nevada，by differential synthetic aperture radar interferometry time series analysis:Probing the lithosphere rheological structure［J］.Journal of Geophysical Research，2007，112(B3):1－18.

25 Dicaprio C，Simons M.The importance of ocean tidal load corrections for differential InSAR［J］.Geophys Res Lett，2008，35(L22309).

26 Lee J S，Papathanassiou K P.A new technique for noise filtering of SAR interferometric phase images［J］.IEEE Trans GRS，1998，36(5):1 456－1 465.

27 王洒，宫辉力，杜钊峰，等.永久散射体干涉测量中最佳主图像选取［J］.测绘学报，2013，42(1):87－93.(Wang Sa，Gong Huili，Du Zhaofeng，et al.Optimal selection of master image in permanent Scatterer InSAR technigue［J］.Acta Geodaetica et Cartographica Sinica，2013，42(1):87－93)

28 Baby H B，Golé P，Lavergnat J，et al.A model for the tropospheric excess path length of radio waves from surface meteorological measurement［J］.Radio Sci，1988，23:1 023－1 038.