基于桥式柔性铰链多误差源的数学建模*

周欢伟，陈 新，陈新度，李克天

（1.广东工业大学，广东广州 510663；2.广州铁路职业技术学院，广东广州 510430）

基于桥式柔性铰链多误差源的数学建模*

周欢伟1,2，陈 新1，陈新度1，李克天1

（1.广东工业大学，广东广州 510663；2.广州铁路职业技术学院，广东广州 510430）

利用快刀伺服系统加工可获得纳米级的微结构，桥式柔性铰链是最关键的零件之一，其柔性铰链的误差度直接影响零件的加工精度。通过对多误差源的分析，探索每个误差源对精度的影响程度。包括过对桥式柔性铰链关键尺寸的加工误差，特别是对敏感度较高的长度、宽度、厚度加工误差的分析，建立起关键尺寸与加工精度的数学模型；分析温度变化，建立基于神经网络的加工误差数学模型，并提出温度补偿的策略；分析重力等原因引起的误差变形，建立由于重力引起变形量与加工精度的数学模型。将上述的多误差源的数学建模运用到设计和制造中，能从源头上减少误差对加工精度的影响程度，提高快刀伺服系统加工微结构零件的尺寸精度和表面粗糙度。

柔性铰链；误差；加工精度；微结构；神经网络

0 引言

柔性铰链是快刀伺服系统中实现微位移的关键零件之一，桥式柔性机构具有拓扑结构简单、应力分布均匀以及固有频率高等特点，目前关于桥式柔性机构的研究报道多见于运动放大机构，Lobontiu等[1]利用卡氏第二定理推导了桥式柔性放大机构刚度的闭环解析公式，并研究了相关几何参数对刚度的影响趋势。Ryu[2]采用矩阵分析的方法对桥式柔性放大机构的变形进行分析，理论结果同实验结果的误差小于10%；Kim等[3]利用同样的方法对空间桥式柔性放大机构(两个二维桥式柔性机构交叉联接)的变形进行分析，通过实验测试，其分析误差也小于10%。柔性铰链的精度包括尺寸精度、表面粗糙度、形位公差等，合理控制零件的加工精度，有利于保证减小加工误差。很多学者对柔性铰链机构的精度进行了较为详细和深入的研究[4-5]，包括制造公差和装配误差的影响，并对误差建模及精度标定等。Niaritsiry等[6]列出了柔性铰链几种缺口的误差，并将这些误差代入整个平面少自由度机构模型进行有限元仿真。叶鑫[7]等人以一种3-PPTTRS微动工作台为例，利用矢量闭环，在微动工作台单支链标准模型的基础上建立基于杆长的误差模型和基于柔性铰链的误差模型。

本文以特定的桥式柔性铰链为研究对象，分析多误差源可能给定位精度带来影响，研究由于加工、温度、重力等的影响，建立与加工精度对应的数学模型，提炼出影响加工精度的敏感元素，从而减少由于误差给精度带来的精度误差。

1 柔性铰链加工误差分析

桥式柔性铰链具有结构对称性强，运动平稳，消除了X、Y轴的耦合性，并且具较大的放大倍数，其具体的拓朴结构示意图如图1所示。

图1 桥式柔性铰链的示意图

1.1 角度误差建模

如图1所示，第1到第8个柔性铰链缺口按直角型设计，第9到第12个柔性铰链按半圆性柔性铰链进行设计。设计时要求柔性铰链l67、l18与水平成72°夹角，左边固定，l12和l56成平行状沿X轴进行移动，由l39、l910、l104、l43构成的驱动刀架部分沿X轴正向平移产生微位移。

但是由于以下制造因素会造成柔性铰链产生的微位移产生误差：（1） l67、l18与水平夹角误差，设计要求成72°夹角，但由于加工为线切割加工，会产生Δα的角度误差；（2）柔性铰链缺口厚度误差，直角缺口设计要求为1.3 mm，半圆缺口设计要求为1.5 mm，但其厚度造成的误差直接影响其刚度；（3）对称度误差分析，设计要求l911、l1012长度相等，达到平行移动，但由于加工误差使得刀架不能完全以水平方式进行平移，会造成位移误差。

由于逆压电效应而产生的微位移为Δh（如图2所示），设计角度为α，由于加工误差，使得本来B点变为B‴，其角度由原来的α变为α-Δα。

图2 角度误差

通过分析可得：按设计要求时，工作微位移为：

压电陶瓷工作微位移为：

ABcosα-ABcosα=x。

由于角度存在误差，工作微位移为：

AB(cosα″-cos(α-Δα))=x′

由于加工误差产生角度误差，使得：

将式（1）、（2）代入（3）得位移误差与角度之间的关系：

1.2 宽度和厚度的误差建模

由于缺口制造过程中产生误差，根据刚度计算能分析出其宽度b对柔性铰链的影响，设计厚度为b，实际加工厚度为b′。根据材料力学的要求，以AB杆的第8点缺口为例进行研究。由于极惯性矩，其刚度为EI，E为该材料的弹性模量，设计厚度b≪t，故此处只研究厚度b对压柔性铰链的影响。如图3所示，其加工厚度误差Δb=b-b′。

图3 宽度加工误差

根据式计算可得：

根据所选材料为304不锈钢时，E为206 GPa，l12=58.9 mm，α=72°，可得出：Δx与Δb的关系。

1.3 长度误差建模

加工过程中，柔性铰链的长度l12与位移的行程相关，通过建模，可得:

当长度由l12变为时，其长度变化为：

2 热误差补偿的数学模型

2.1 基于RBF的神经网络模型的热误差模型

（1）RBF的神经网络模型的数学模型

RBF（Radical Basis Function）神经网络即径向基函数神经网络是一种高效的前馈式神经网络，它具有其他前向网络所不具有的最佳逼近性能和全局最优特性，并且结构简单，训练速度快。同时，它也是一种可以广泛应用于模式识别、非线性函数逼近等领域的神经网络模型。

在理论上，RBF网络和BP（Back Propaga⁃tion）多层前馈网络都是以任意精度逼近任何非线性函数。它们使用的中隐层节点的基函数都采用了“高斯条函数”，但RBF网络将每个输入维的高斯响应加权求和，使得其成为具有唯一最佳逼近的特性的神经网络系统，且无局部极小问题存在。

式中：i表示第i个高斯条单元(即隐层节点i)； j表示输入维， M为其维数； xj、cij、σij、wj分别是输入向量X和第i个高斯条函数的中心ci、宽度σj以及权矢量Wi的第 j项。

（2）热应力的产生原因

桥式柔性铰链热应力变形的主要来源为：1）在桥式柔性铰链内，当温度场的变化时，金属外表面与内部之间因膨胀不同而相互牵制，引起强迫膨胀或约束，使得尺寸变化不一致产生变形；2）当温度场均匀时，对于同一物体由于热胀冷缩的原因，促使产生热变形，几何尺寸发生变化。

柔性铰链在不同方向上的变形位移分量ux、uy、uz是连续存在的。应变分量是两部分之和：一部分由应力引起的，一部分由温度变化引起的，根据虎克定律有：

上式可用矩阵形式表示为：

εx、εy、εz：分别表示x、y、z三个方向的应变量；

σx、σx、σx：分别表示x、y、z三个方向的应力；

γxy、γyz、γzx：分别在xy、yz、zx三个平面的剪切应变量；

τyz、τyz、τzx：分别在xy、yz、zx三个平面的剪应力；

G：剪切弹性模量；T：变温；

α：热膨胀系数。

2.2 热误差计算

金属具有热胀冷缩的属性，柔性铰链由于温度变化使得缺口加工精度对定位精度产生影响。由于柔性铰链各部分结构尺寸不同，环境温度的变化结构膨胀大小不一，具体伸长长度如下：

根据304钢的热膨胀系数为 α=170×10-7/℃，根据设计，铰链固定端7、8点，构成3、4、9、10的平台的，7点到10点的距离l1= 128.2 mm。根据式（6）所示，温度升高1°C，则ΔL=2.179 4 μm。

2.3 基于RBF的热误差补偿方法

快刀伺服系统的误差受加工条件以及周围环境等多种因素的影响，呈现非线性及交互作用。为提高加工精度，需采取有效的措施减少热误差，通过温度传感器而在实时补偿过程中用机床温度值来预报热误差。

神经网络理论是利用工程技术手段模拟人脑神经网络结构和功能的一种非线性动力学系统[8]。以神经网络为代表的智能补偿技术已运用到热误差建模中[9-11]，一般采用BP算法的前传多层感知器网络，根据感知器网络权重初始化的随机性，难以根据热误差的实际情况确定一组较好的初始值。而RBF理论提供了一种新颖而有效的手段，能有效地将BF结合起来，把由于温度误差通过神经网络有效地进行补偿。

3 缺口处重力变形的误差模型

3.1 重力对加工误差的影响规律

快刀伺服系统中桥式柔性铰链、拉杆1、拉杆2、压电陶瓷、刀具等存在本身的重力（如图4所示），使缺口部分受重力因素产生变形，引起位移刀尖位移的定位精度产生误差，而对工件的加工精度影响是很难进行修改和补偿的，所以分析缺口处重力变形的误差是十分重要的。

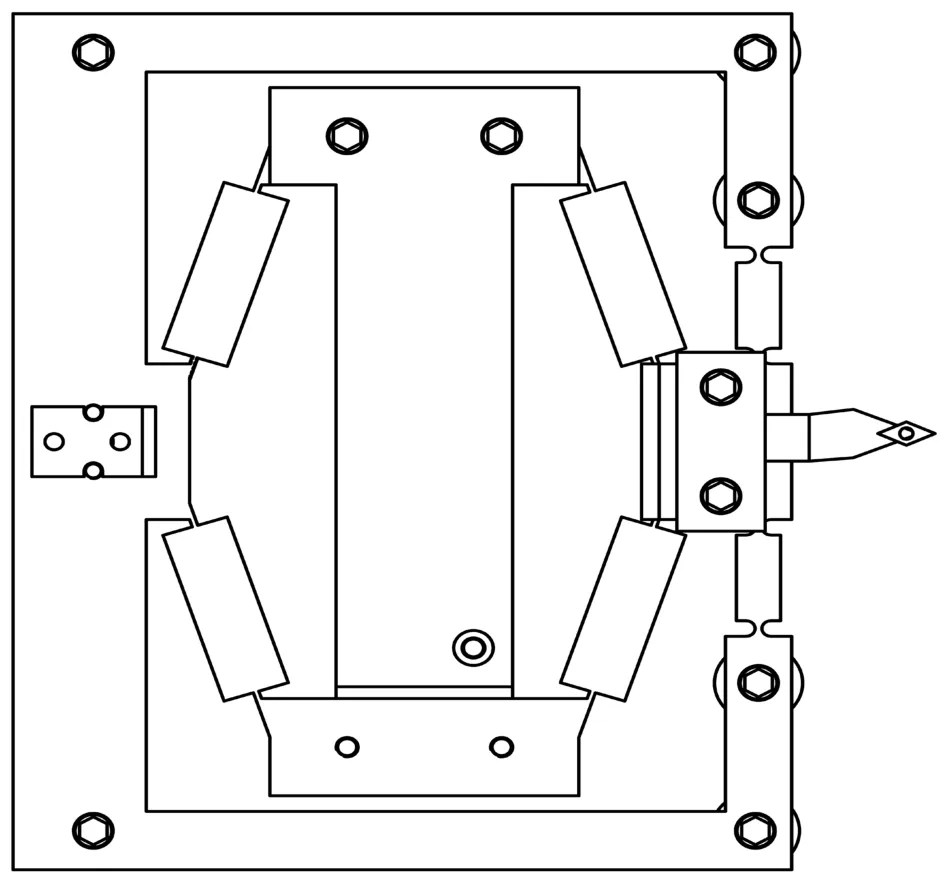
图4 快刀伺服系统的重力变形模型

假设零件的重力为G，长度为l，刚度为EI，根据材料力学公式可得：

快刀伺服系统中，直接由于重力影响桥式柔性铰链变形的零件有桥式柔性铰链、上拉杆、下拉杆、刀具、刀具固定板、螺栓等。其重力可进行等效，并针对10个缺口处计算变形量，通过式（7）可计算获得变形量。

3.2 重力误差仿真分析

将快刀伺服系统用Pro/Engineer进行三维数字建模，利用Ansys仿真软件，得到如图5所示的变形量。从图5中可得出最大处变形量为4.4μm，并且在拉杆中部，对刀具的加工精度影响不大。

图5 重力仿真分析

4 小结

本文通过对快刀伺服系统的由于加工精度误差、温度变化而引起的定位误差进行分析。首先对柔性铰链的转角误差进行分析，建立由于加工误差而引起的转角误差和刀尖处定位精度的关系。然后探索柔性铰链缺口宽度、厚度的误差引起刀尖处定位误差的关系，建立了它们的数学模型，最后分析柔性铰链的杆长误差，建立长度误差与定位精度的数学模型。

探索温度的变化引起定位精度变化的规律，建立虎克定律方程的数学模型，根据温度变化程度，构建温度误差引起的定位精度误差的数学模型。根据重力大小，用Ansys对得力进行分析，得出因重力引起的变形误差方向。

［1］Lobontiu N，Garcia E.Analytical model of displacement amplification and stiffness optimization for a class off 1ex⁃ure based compliant mechanism［J］.computers and structures，2003（81）：2797-2810.

［2］Ryu Jw.6-Axis Ultra-precision Positioning Mechanism Design and Positioning Control［D］.Daeje 0n：Korea Advanced Institute of Science and Technology，1997.

［3］Kim J H，Kims H，Kwak Y K.Development and optimi⁃zation of 3-D bridge type hinge mechanisms［J］.Sen⁃sorsand ActuatorsA： Physical， 2004（116）：530-538.

［4］Wang Jian.MASORY O on the accuracy of a stewart plat⁃form-Part l： the effect of manufacturing tolerances［A］./IEEE International Conference on Robotics and Automation Los［C］，May 2-6，1993，Atlanta，GA，USA.New York：IEEE，203：114-120.

［5］李嘉.6-Pss并联微动机器人设计研究［D］.北京：清华大学，2000.

［6］NIARITSIRY T F，FAZENDAT N，CLAVELR.Simula⁃tion analysis of the sources of inaccuracy of a parallel ma⁃nipulator［A］./IEEE International Conference on Ro⁃botizes， IntelligentSystems and signalProcessing［C］，October 2003，Changsha，China.New York：IEEE，2 004：266-271.

［7］叶鑫，张之敬，万毕乐，等.微动工作台的误差源分析［J］.机械工程学报，2009，45（1）：258-266.

［8］焦李成.神经网络系统理论［M］.西安：西安电子科技大学出版社，1990.

［9］Yang S，Yuan J，Ni J.The improvement of thermal error modeling and compensation on machine tools by cams neural net work［J］.International Journal of Machine Tools and Manufacture，1996，36（4）：527-537.

［10］Vanherck P，Dehaes J，Nuttin M.Compensation of thermal deformations in machine tools with neural nets［J］.ComputersinIndustry， 1997， 33（1）：119-125.

［11］Mize C D，Ziegert J C.Neural network thermal error compensation of a machining center［J］.Precision Engi⁃neering，2000，24（4）：338-346.

The Mathematical Modeling of Multi-Error Source Based on Bridge Type Flexure Hinge

ZHOU Huan-wei1，2，CHEN Xin1，CHEN Xin-du1，LI Ke-tian1
（1.Guangdong University of Technology，Guangzhou510663，China；2.Guangzhou Institute of Railway Technology，Guangzhou510430，China）

Using fast tool servo system to machine the nanometer grade micro-structure，the bridge flexure hinge is a key part.The error of flexure hinge directly affects the machining accuracy of micro-structure.This paper explores the influence degree on the accuracy through analyzing all kinds of error source.The mathematical model of key dimension and machining accuracy is established including the machining error of bridge flexure hinge，which includes the sensitive size of length，width and thickness.After analyzing temperature change，the mathematical model of machining error is established based on neural network and the temperature compensation strategy is put forward.After Analyzing the reasons of deformation error caused by gravity，the mathematical model of deformation and machining precision is established.The above mathematical modeling applied for the design and manufacturing process can reduce their influence on machining accuracy，and it also can help the fast tool servo system to improve micro-structure size precision and surface roughness.

flexure hinge；error；machining accuracy；micro-structure；neural networks

TP391.7

A

1009－9492(2014)09－0009－05

10.3969/j.issn.1009-9492.2014.09.003

周欢伟，男，1977年生，江西九江人，博士研究生，副教授。研究领域：快刀伺服系统，纳米加工。

(编辑：阮 毅)

*广东省引进创新科研团队计划（编号：201001G0104781202）

2014－07－28