利用高阶累积量实现数字调制信号的识别*

郭娟娟,尹洪东,姜 璐,梅恒芳

(中国石油大学(北京) 地球物理与信息工程学院,北京102249)

利用高阶累积量实现数字调制信号的识别*

郭娟娟,尹洪东,姜 璐,梅恒芳

(中国石油大学(北京) 地球物理与信息工程学院,北京102249)

文中提出一种基于高阶累积量识别多种数字调制信号的算法。首先推导计算各信号的八阶累积量,从二、八阶累积量中提取一个特征参数,实现以更少参数识别更多信号的目的;然后,为提高MFSK的识别率,从微分后MFSK信号的四、六阶累积量中提取一个特征参数完成识别。仿真结果显示,通过利用这两个参数可以实现2ASK/BPSK、4ASK、8ASK、QPSK、8PSK、2FSK、4FSK、8FSK、16QAM、64QAM等多种数字调制信号的识别。

调制识别 高阶累积量 特征参数

0 引 言

随着全空域信号复杂度的增高,信号的调制方式也趋于多元化,对信号调制方式识别的研究具有更加重要的意义。调制识别在军用和民用领域都有很高的实用价值:军用方面,调制识别是通信电子战中的关键技术,利用它可实现对敌方的干扰和监听;民用方面,采用调制识别可以实现无线电监测的智能化。

数字调制信号的识别技术是以未知调制信息的内容为前提的,即确定信号所采用的调制方式以及估计出信号的某些调制参数,为信号的后续处理提供依据。目前识别调制信号的方法多种多样:通过计算5个瞬时特征参数,实现6种典型信号的调制识别[1];利用小波系数作为特征值信号进行调制识别[2];利用高阶累积量和支持向量机相结合的方法来识别调制信号[3]。由于高斯白噪声高于二阶的累积量恒为零,因此基于高阶累积量的数字调制信号的识别方法具有良好的抗噪性能,在调制识别领域受到了广泛的重视。

就高阶累积量识别调制信号的技术而言,利用高阶累积量和分形盒维数相结合实现2ASK、4ASK、BPSK、4PSK、2FSK、4FSK、16QAM七种信号的识别[4];利用四、六阶累积量和支持向量机的方法实现2ASK、4ASK、8ASK、4PSK、8PSK信号的识别[5];对比分析四阶和六阶累积量识别MPSK信号,证明六阶具有更好地抗多径干扰的能力[6];利用四阶和八阶累积量的特征对π/4-QPSK、8PSK信号进行识别[7]。本文主要推导计算了各类调制信号的八阶累积量,从而解决了二、四、六阶累积量未能识别8ASK信号和MQAM信号的问题;此外,为提高MFSK的识别率,从微分后MFSK信号的四、六阶累积量中提取一个特征参数完成MFSK信号的类间识别。通过理论推导以及仿真验证,实现2ASK/BPSK、4ASK、8ASK、QPSK、8PSK、2FSK、4FSK、8FSK、16QAM、64QAM等多种数字调制信号的识别。

1 高阶累积量调制识别分析

1.1 高阶矩和高阶累积量

对于平稳连续随机信号X(t),令X1=X(t),X2=X(t+τ1),…Xk=X(t+τk-1),则随机信号X(t)的k阶累积量可定义为[8]:

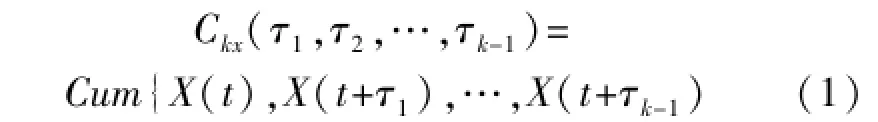
对于平稳复随机过程{X(t)},其k阶混合矩可表示为[9]:

式中,X*(t)表示函数X(t)的共轭。

随机信号的矩和累积量存在如下的转换关系[10]:

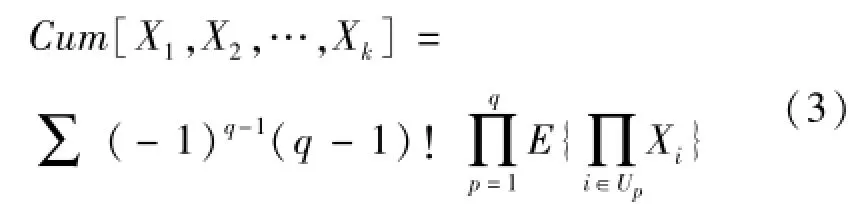
式中,∑(·)表示在所有的互不连通有序分割合集X=(X1,X2,…,Xk)内求和,q表示分割的子集数,Up表示在q个子集当中第p个子集中元素的下标集。

因此,具有零均值的平稳复随机过程X(t)的高阶累积量可表示为:

1)二阶累积量:

2)四阶累积量:

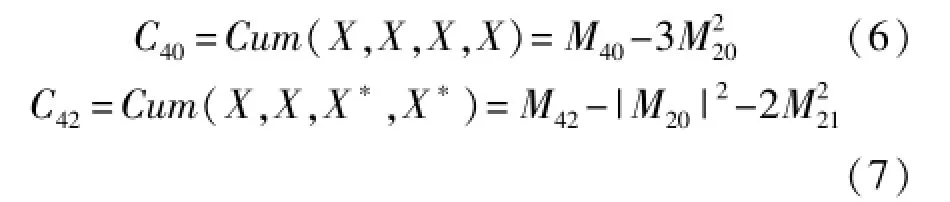
3)六阶累积量:

4)八阶累积量:

1.2 数字调制信号模型描述

通常接收到的受到噪声污染的数字调制信号的复数形式可表示为[11]:

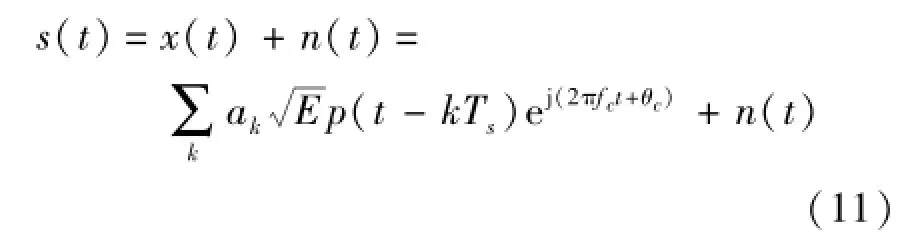
式中,k=1,2,…,N,N为发送码元序列的长度,ak表示码元序列;p(t)为基带码元波形,Ts为码元宽度,fc为载波频率,θc为载波相位,E为信号的能量;n(t)为零均值的复高斯白噪声,与发送信号x(t)相互独立。

在接收端,对已调信号经过预处理,在实现载波频率、相位、定时同步的前提下,下变频后的复基带信号可表示为:

式中,Δθc为载波相位差。

根据数字调制信号的原理,将式(12)中各类数字调制信号中的ak表示为

MASK信号:

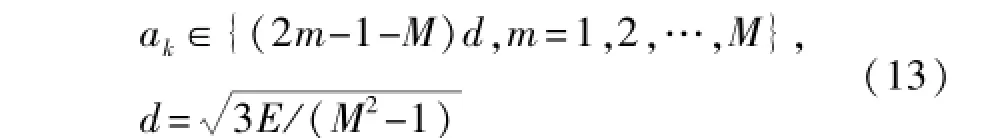
MPSK信号:

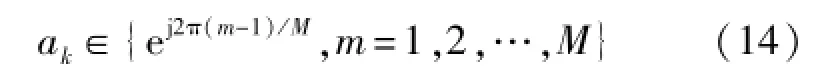
MFSK信号:

式中,fk∈{(2m-1-M)Δf/2π,m=1,2,…,M},Δf为MFSK信号的频偏。

MQAM信号:

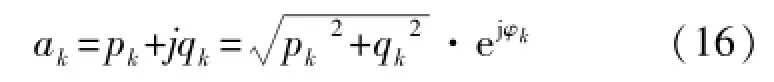
式中,pk,qk∈{(2m-1-)d,m=1,2,…,},,φk=arctan(qk/pk)。

1.3 数字调制信号高阶累积量的理论值

对于任何零均值高斯随机过程,其高阶(高于二阶)累积量恒为零[8],并且累积量相对其变元具有可加性,因此,接收信号的累积量可用发送信号的累积量代替,而不受高斯白噪声的影响。

假设信号的能量为E,依据文献[12]中提出的利用算数平均来代替统计平均的方法,计算数字调制信号的高阶累积量,各类信号的高阶累积量的理论值如表1所示。

表1 数字调制信号的累积量值Table 1 High-order cumulants of digital modulation signals

由表1可知2ASK信号和BPSK信号的累积量相同,即无法用累积量进行识别,所以后续研究中将这两种信号看为一类。累积量只包含幅度和相位信息,无法体现频率上的差异,由表1亦可知MFSK的各阶累积量相同,无法利用累积量直接实现MFSK的类间识别,因此需要把MFSK信号的频率信息转化为含有幅度信息的信号。因此,将式(15)代入式(12),并对其求一阶导数,可得[13]:

式中,第一项是一个冲击函数,第二项则是一含有幅度信息的频率调制信号,对式(17)进行中值滤波,滤除冲击函数的影响,可得:

式中,n′(t)依然近似是高斯白噪声。计算s′(t)的高阶累积量,如表2所示。

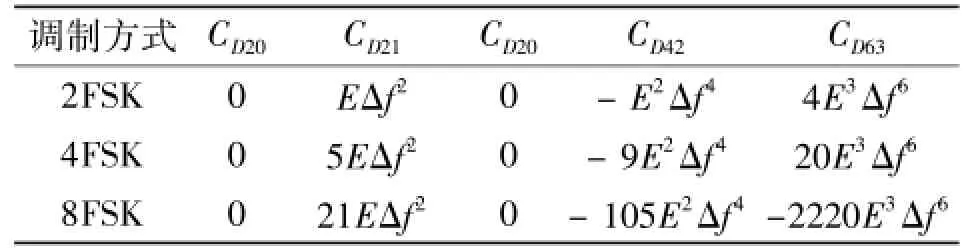
表2 微分后MFSK信号的高阶累积量Table 2 High-order cumulants of MFSK signal after differential calculation

由表2可见,MFSK信号经微分后,各阶累积量有明显的差别,所以可以利用高阶累积量对MFSK信号实现类间识别。

2 特征参数选取

选取特征参数时,一方面,使用信号各阶累积量的绝对值,能减弱相位抖动对特征参数的影响;另一方面,特征参数均采用比值的形式,可消除幅度对特征参数的影响[14]。经过分析,各种调制信号的八阶累积量C80的理论值存在较大的差别,所以可以利用C80完成除MFSK信号之外的数字调制信号的识别,选取如下的特征参数:

因此,各数字调制信号的特征参数fs1的理论值如表3所示。

表3 各调制信号的特征参数理论值Table 3 Theoretical value of the characteristic parameter of digital modulation signals

对于MFSK信号,微分后进行中值滤波,再选取一个特征参数:

因此,MFSK信号的特征参数fs2的理论值如表4所示。

表4 微分后MFSK信号的特征参数理论值Table 4 Theoretical value of the characteristic parameter of MFSK signal after performing differential

由表4可知利用特征参数fs2可以实现MFSK信号的类间识别。由于高斯白噪声三阶及三阶以上的累积量恒为零,为提高信号的识别率,从微分后信号的四阶和六阶累计量中提取特征参数。

3 算法步骤及验证

3.1 算法步骤

利用上述两个参数完成数字调制信号的识别,算法的具体步骤如下:

1)对接收到的信号通过下变频变换到基带,再通过低通滤波器滤除信号的2倍频分量。

2)计算基带信号的二、四、六、八阶累积量,并求特征参数fs1。

3)利用特征参数fs1,通过设置合适的阀值,将各数字调制信号区分为以下几类:2ASK/BPSK, 4ASK,8ASK,QPSK,8PSK,MFSK,16QAM,64QAM。

4)若fs1的值为0,对信号微分处理后进行中值滤波,计算其二、四、六阶累积量,求出特征参数fs2,实现MFSK的类间识别。

3.2 算法仿真验证

根据上述分析,对本文提出的识别算法采用Matlab仿真进行验证,分别对特征参数和识别性能进行仿真及分析。

实验一:各调制信号的两个特征参数随信噪比变化的情况研究。

采用Matlab中产生的随机序列作为信号源,设定信号的载波频率为10 kHz,采样频率为60 kHz,码元速率为1 000 b/s,MFSK信号的频偏为5 kHz,数据长度为3 000个,噪声为高斯白噪声,信噪比从0～30 dB(步长为1 dB)。同一信噪比下,对两个特征参数进行100次仿真计算后取平均值。

由于特征参数fs1的幅值范围较大,为了便于观察仿真结果,将其划分为3段([0,3]、[3,40]、[40, 300]),分别画出各调制信号的特征参数fs1随信噪比的变化曲线,如图1所示。

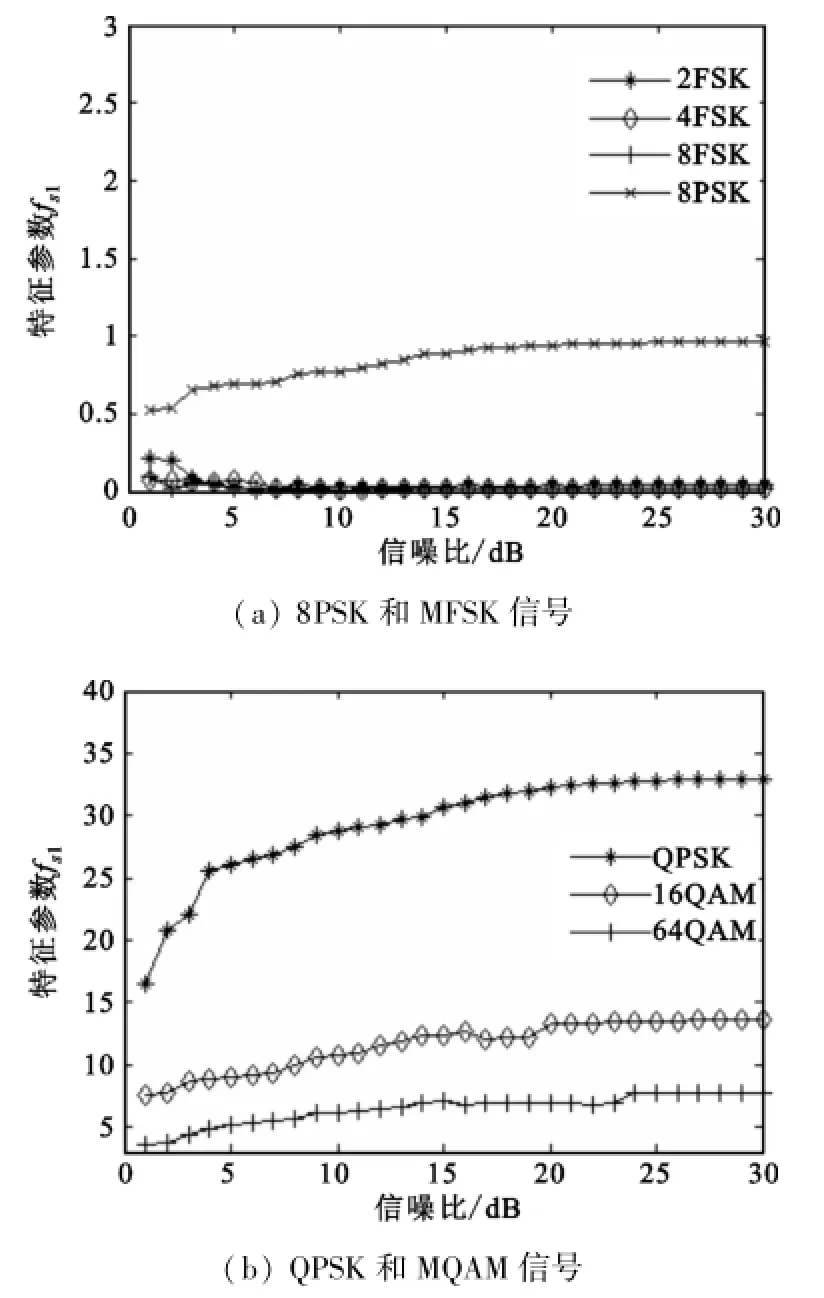
图1 不同信噪比下特征参数fs1的值Fig.1 Values of fs1 with different SNRs

由图1看出,除MFSK信号以外,各类数字调制信号的特征参数fs1的仿真值有明显的差别,分别都与各自的理论值相近,证明了从八阶累积量中选取的特征参数fs1的正确性。对比文献[15],本文特征参数的选取可实现更少参数识别更多调制信号的目的,并且证明八阶累积量比六阶累积量具有更好的识别效果。

微分后MFSK信号的特征参数fs2随信噪比的变化曲线如图2所示。

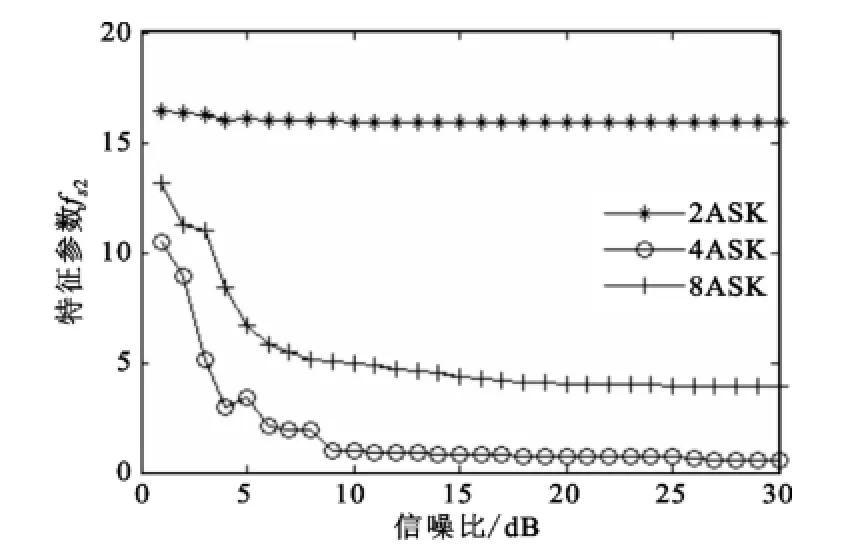
图2 不同信噪比下MFSK信号特征参数fs2的值Fig.2 Values fs2 of MFSK with different SNRs

由图2可知,MFSK信号的特征参数fs2的仿真值接近于理论值,不同信噪比下有明显的差别,证明了利用特征参数fs2实现MFSK信号类间识别的正确性。由于高斯白噪声的二阶累积量不为零,文献[15]中从二、四阶累积量中选取的特征参数受噪声的影响较大,而本文从四、六阶累积量中选取的特征参数fs2,能消除噪声对实现MFSK信号类间识别产生的影响。

实验二:各调制信号识别性能的仿真研究。

根据实验一的仿真结果,确定各种信号的判别阀值,特征参数fs1的阀值按照仿真值的大小依次选为:0、1、6.5、12、34、70、120、260,特征参数fs2阀值选为:0.5、4、16。依照算法步骤进行Matlab仿真,设信号的载波频率为10 kHz,采样频率为60 kHz,码元速率为1 000 b/s,MFSK信号的频偏为5 kHz,数据长度为3 000个,噪声为高斯白噪声,信噪比为0～30 dB(步长为1 dB)。同一信噪比下,对所有信号分别进行1 000次仿真,取识别正确的次数和总仿真次数的比值作为识别率。仿真结果如图3所示。

图3 识别率随信噪比的变化Fig.3 Recognition rates with different SNRs

由图3可知,采用本文提出的识别算法,MASK信号和BPSK信号7 dB以上的识别率达到91%以上,QPSK和8PSK信号6 dB以上识别率能达92%以上,MFSK信号和MQAM信号5 dB以上识别率能达94%以上,8 dB以上所有的信号识别率都能达到较高水平。本文中提出的特征参数可以识别文献[15]未能识别的8ASK信号、8PSK信号和64QAM信号,采用四、六阶累积量,使MFSK信号在低信噪比下具有更高的识别率;对比文献[16],本文选取的特征参数更少、识别复杂度更低,并且能更多地识别出8ASK、8FSK以及MQAM信号,信噪比低于8 dB时各类调制信号的识别率也能达到更高。

4 结 语

本文基于高阶累积量的理论基础,推导计算数字调制信号的八阶累积量,从中选取特征参数实现数字调制信号的识别,对于MFSK信号,微分后计算四、六阶累积量并提取特征参数,有效的抑制了噪声的影响并且提高了低信噪比下的识别率,经实验仿真证明该算法能有效的识别2ASK/BPSK、4ASK、8ASK、QPSK、8PSK、2FSK、4FSK、8FSK、16QAM、64QAM等多种数字调制信号。该算法选取的特征参数少,降低了识别的复杂度,并得到了更高的识别率,充分证明改进后的特征参数具有更高的实用价值,为信号的后续处理提供参考。然而本文的信号模型假设信道是高斯噪声信道,后续研究需要考虑实际复杂噪声通道以及多路径通道的影响。

[1] 付仕平,杨丽,邵伟.基于瞬时特征参数的数字信号调制识别算法[J].现代防御技术,2013,41(06):71-75.

FU Shi-ping,YANG Li,SHAO wei.Digital Signal Modulation Classification Algorithm Based on Instantaneous Parameter[J].Modern Defense Technology,2013,41 (06):71-75.(in Chinese)

[2] Ho K C,Prokipiw W,Chan Y T.Modulation Identification of Digital Signals by the Wavelet Transform[J].Radar,Sonar and Navigation,IEEE Proceeding,2000,147 (04):169-176.

[3] Li Pei-hua,Zhang Hong-xin,Wang Xu-ying,et al. Modulation recognition of communication signals based on high order cumulants and support vector machine[J]. The Journal of China Universities of Posts and Telecommunications,2012,19(Suppl.1):61-65.

[4] 党月芳,徐启建,张杰,等.高阶累积量和分形理论在信号调制识别中的应用研究[J].信号处理,2013,29(06):761-765. Dang Yue-fang,Xu Qi-jian,Zhang Jie,et al..Research on Modulation Classification Based on High-order-Cumulants and Fractal Theory[J].Journal of Signal Processing,2013,29(6):761-765.(in Chinese)

[5] 王兰勋,任玉静.基于累积量和SVM的数字调制识别[J].通信技术,2009,42(11):46-47,51.

WANG Lan-xun,REN Yu-jing.Recognition of Digital Modulation Signals Based on High-Order Cumulants and Support Vector Machines[J].Communications Technology,2009,42(11):46-47,51.(in Chinese)

[6] 孙钢灿,王忠勇,刘正威.基于高阶累积量实现数字调相信号调制识别[J].电波科学学报,2012, 27(04):825-831.

SUN Gang-can,WANG Zhong-yong,LIU Zheng-wei.Performance Analysis of Modulation Recognition of MPSK Signal based on High-order Cumulants[J].Chinese Journal of Radio Science,2012,27(04):825-831.(in Chinese)

[7] 陆凤波,黄知涛,易辉荣,等.一种基于高阶累积量的数字调相信号识别方法[J].系统工程与电子技术, 2008,30(09):1611-1615.

LU Feng-bo,HUANG Zhi-tao,YI Hui-rong,et al.. Recognition algorithm of phase shift keying signals by higher-order cumulants[J].Systems Engineering and E-lectronics,2008,30(09):1611-1615.(in Chinese)

[8] 张贤达.现代信号处理[M].第2版.北京:清华大学出版社,2002:263-274.

ZhANG Xian-da.Modern Signal Processing[M].Second Edition.Beijing:Tsinghua university,2002:263-274.(in Chinese)

[9] Shermeh A.E,Ghazalian R.Recognition of Communication Signal Types Using Genetic algorithm and Support Vector Machines based on the Higher-order Statistics[J]. Digital Signal Processing,2010,20(06):1748-1757.

[10] 池文静.复杂调制信号调制样式识别方法的研究[D].西安:西安电子科技大学,2011:17-21.

CHI Wen-jing.Research on Modulation Classification of Complexly Modulated Signals[D].[Master dissertation], Xi'an:Xidian University,2011:17-21.(in Chinese)

[11] Proakis J G.Digital Communication[M].4thed.New York:McGraw-HillBook Co.,2001:169-201.

[12] Swami A,Sadler B M.Hierarchical Digital Modulation Classification Using Cumulants[J].IEEE Transactions on Communications,2000,48(03):416-429.

[13] 吕新正,魏平,肖先赐.利用高阶累积量实现数字调制信号的自动识别[J].电子对抗技术,2004,19 (06):3-6.

LV Xin-zheng,WEI Ping,XIAO Xian-ci.Automatic Identification of Digital Modulation Signals Using High Order Cumulants[J].Electronic Information Warfare Technology,2004,19(06):3-6.(in Chinese)

[14] 位小记,谢红,郭慧.基于高阶累积量和星座图的调制识别算法[J].哈尔滨商业大学学报:自然科学版, 2011,27(04):609-613.

WEI Xiao-ji,XIE Hong,GUO Hui.Algorithm of Modulation Recognition based on High order Cumulant and Constellation[J].Journal of Harbin University of Commerce(Natural Sciences Edition),2011,27(04):609 -613.(in Chinese)

[15] 包锡锐,吴瑛,周欣.基于高阶累积量的数字调制信号识别算法[J].信息工程大学学报,2007,80(04): 463-467.

BAO Xi-rui,WU Ying,ZHOU Xin.Algorithm of Digital Modulation Recognition Based on Higher-Order Cumulants[J].Journal of Information Engineering University,2007,8(04):463-467.(in Chinese)

[16] 张弛,吴瑛,周欣.基于高阶累积量的数字调制信号识别[J].数据采集与处理,2010,25(05):575-579.

ZHANG Chi,WU Ying,ZHOU Xin.Digital Modulation Recognition Based on High-Order Cumu lants[J]. Journal of Data Acquisition&Processing,2010,25 (05):575-579.(in Chinese)

GUO Juan-juan(1989-),female,graduate student,majoring in signal detection and processing.

尹洪东(1963-),男,博士,副教授,主要研究方向为信号检测采集与处理;

YIN Hong-dong(1963-),male,Ph.D.,associate professor,majoring in signal detection acquisition and processing.

姜 璐(1989-),男,硕士研究生,主要研究方向为信号检测与采集;

JIANG Lu(1989-),male,graduate student,majoring in signal detection and acquisition.

梅恒芳(1989-),男,硕士研究生,主要研究方向为信号检测与采集。

MEI Heng-fang(1989-),male,graduate student,majoring in signal detection and acquisition.

Recognition of Digital Modulation Signals via High-Order Cumulants

GUO Juan-juan,YIN Hong-dong,JIANG Lu,MEI Heng-fang
(College of Geophysics and Information Engineering,China University of Petroleum,Beijing 102249,China)

An algorithm based on HOC(high-order cumulants)for recognizing multiple digital modulation signals is proposed.The eight-order cumulants are firstly deduced and calculated,and one feature parameter extracted from two-order and eight-order cumulants is used to recognize more signals with less parameter.Then,in order to increase the recognition rate of MFSK signals,another feature parameter is picked up from four-order and six-order cumulants of MFSK signal.Simulation shows that numerous digital modulation signals such as 2ASK/BPSK,4ASK,8ASK,QPSK,8PSK,2FSK,4FSK,8FSK,16QAM, 64QAM can be identified by these two parameters.

modulation recognition;high-order cumulant;feature parameter

TN911.72

A

1002-0802(2014)11-1255-06

10.3969/j.issn.1002-0802.2014.11.004

郭娟娟(1989-),女,硕士研究生,主要研究方向为信号检测与处理;

2014-08-08;

2014-09-15 Received date：2014-08-08;Revised date：2014-09-15