基于改善Tent混沌映射的宽间隔跳频序列的构造*

马世旺,陆锐敏,赖 平,张严平

(1.解放军理工大学通信工程学院,江苏南京210007;

2.南京电讯技术研究所,江苏南京210007; 3.中国人民解放军63981部队,湖北武汉430311)

基于改善Tent混沌映射的宽间隔跳频序列的构造*

马世旺1,陆锐敏2,赖 平3,张严平1

(1.解放军理工大学通信工程学院,江苏南京210007;

2.南京电讯技术研究所,江苏南京210007; 3.中国人民解放军63981部队,湖北武汉430311)

跳频序列是跳频通信的关键技术之一,基于混沌映射产生跳频序列是目前较为常用的一种方式。针对单一映射产生的跳频序列存在抗预测能力不强和有限精度的问题,文章采用Jacobi序列扰动级联Logistic映射和Tent映射产生的跳频序列,并利用模d加余算法进行宽间隔处理的方法。仿真分析表明,文章所得到的跳频序列在均衡性,随机性,汉明相关性,复杂度以及平均跳频间隔等方面能够较好满足跳频通信对跳频序列的要求。

跳频序列 宽间隔 级联映射 序列扰动

0 引 言

跳频序列用来控制跳频通信中载波频率跳变的伪随机序列,通常产生跳频序列的方法有基于有限域、基于分组密码、基于混沌映射以及差分跳频序列的方法[1]。上世纪60年代混沌映射理论进入人们的研究领域,凭借其良好的初值敏感度和任意周期的特点在跳频序列的设计中得到了关注。已经有诸多文献研究了基于混沌映射产生跳频序列,此类文献可以参考[2-4]。对产生的跳频序列宽间隔处理可以有效提升序列的抗窄带干扰、部分频带阻塞干扰、跟踪干扰以及多径效应[5]。序列宽间隔处理的一些方法可以参考文献[5]。

目前,为了克服混沌序列的有限精度问题,通常采用添加扰动的方法,如利用m序列对混沌序列进行扰动[6]。但是,对于m序列的研究已经很多,而且m序列的生成多项式较固定,容易被穷举攻击。因此,文章采用具有更高的复杂度和安全性的Jacobi序列对基于级联改善Tent混沌映射和Logistic映射产生的序列进行扰动。最后利用模d加余算法对产生的跳频序列进行宽间隔处理。

文章的安排如下,在第1部分介绍了级联混沌映射、Jacobi序列、模d加余算法;第2部分对文章产生的序列进行性能仿真;最后对文章做了总结性表述并对后续工作进行了说明。

1 基于级联混沌映射产生跳频序列

1.1 级联混沌映射

选用Tent映射是因为其具有良好的遍历均匀性,但是其随机性并不是很理想,因此,文献[7]提出了分段Tent混沌映射,并证明其性能得到了改善。同时,由于计算机运算的精度有限,混沌吸引子轨迹的周期不可能无限长,文献[8]经过分析证明,使用级联的混沌映射可以避免这种情况以产生更长的序列,而且级联的次数越高,产生的跳频序列的周期越长。因此,文章采用分段Tent混沌映射与常用的改进的Logistic映射进行级联产生混沌序列。

Logistic映射定义为:

通用Tent混沌映射定义为:

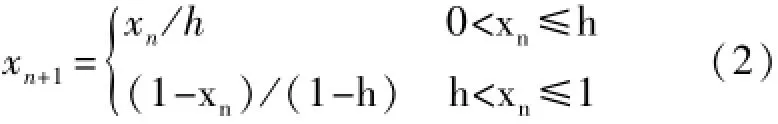
经过改善的2N分段Tent映射表达式为(3):

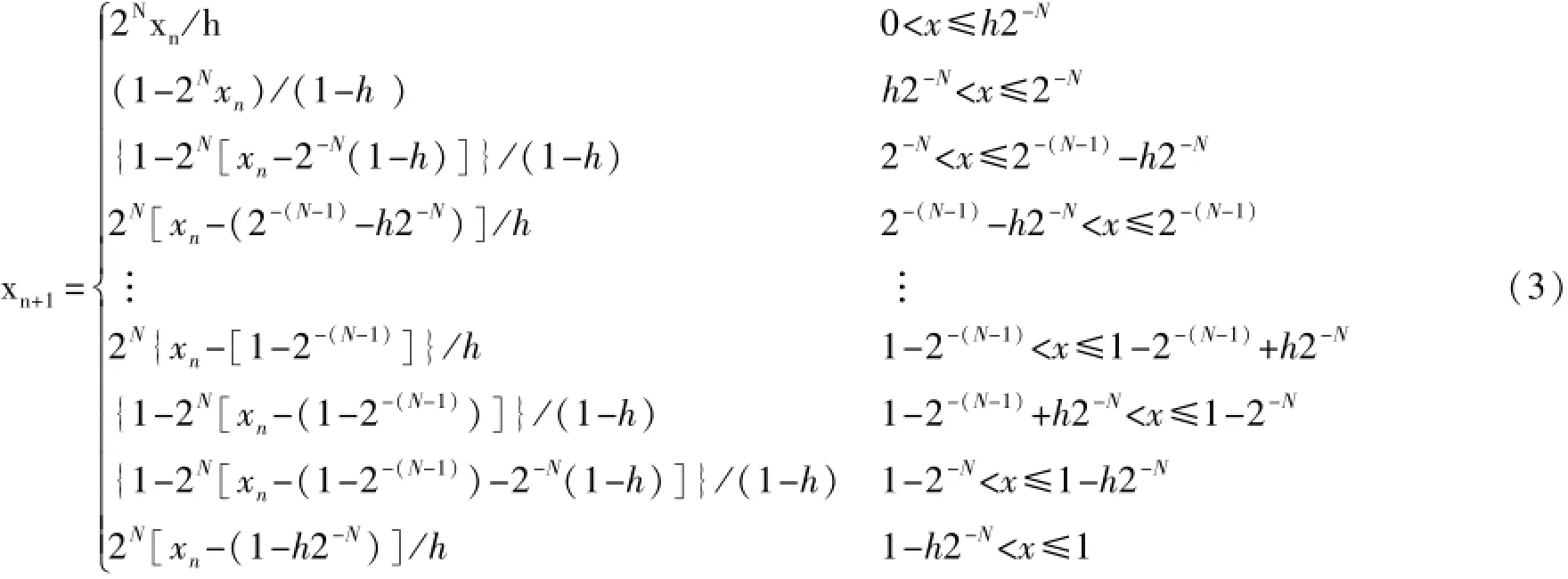
1.2 Jacobi序列

首先介绍二次剩余、Legendre符号和Legendre序列的概念。

1)二次剩余:设p＞1,若x2≡n(modp),同时gcd (p,n)=1有解,则n叫做模数p的二次剩余;若无解,则n叫做模数p的二次非剩余。

2)Legendre符号:设p为奇素数且gcd(p,n)= 1,则Legendre符号定义如下:

3)Legendre序列:设p为任意素数,周期为p的Legendre序列s′=(s0′,s1′,…,sp-1′)定义为si′=。习惯将s'转化为0,1序列s:

将Legendre序列拓展到n=pq(p、q为任意素数)的情况,便产生了Jacobi序列。目前Jacobi序列主要有四种:Jacobi序列,修改的Jacobi序列,多值Jacobi序列及广义Jacobi序列,它们都具有很好的伪随机性能。周期n=pq的Jacobi序列s=(s0,s1,…,sn-1,)定义为:

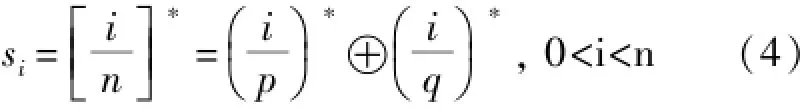
选用m序列对产生的跳频序列进行扰动可以得到性能优良的跳频序列。但是m序列生成多项式是固定且有限的,而基于Jacobi序列产生的扰动序列具有灵活的选择与组合形式,同时Jacobi序列具有优良的汉明相关性能以及较高的线性复杂度[9],选用Jacobi序列对级联混沌映射产生的序列进行扰动能有效的提高系统的安全性。

1.3 模d加余算法

此算法在文献[10]中提出,该算法是对目前常用的对偶频带法的有效改进,在频隙总数为q,最小频隙间隔为d,序列长度为N的条件下,该算法可以表述如下:

1)依据混沌映射产生的序列建立频带F1和F2

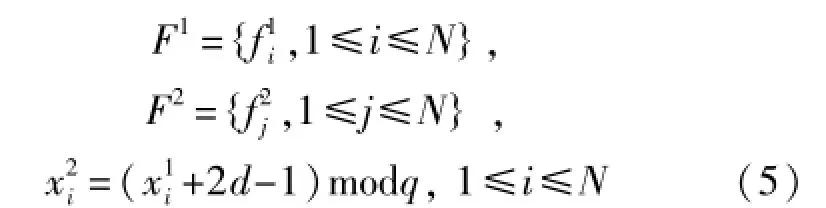
1.4 跳频序列的产生

1)以TOD为初始迭代点,利用8分段Tent映射产生N0+N1个迭代点,若TOD的值用n位二进制数表示为TOD=bn-1,bn-2,…,b2,b1,b0。则当前TOD0的获得可以参考下式;

2)舍弃1)中产生的前N0个迭代值,将之后的N1个迭代值作为Logistic映射的初始迭代值,产生N1×N2个迭代点;

3)将2)产生的值量化为二进制序列,以产生的Jacobi序列对其进行扰动;

4)将最终得到的N1×N2个比特进行映射。{0,1}→{0,1,2…,q-1}

2 跳频序列性能检测

对跳频序列性能的检测通常会采用均衡性、随机性、汉明相关性、复杂度以及平均间隔等参数,下面对文章产生的跳频序列的上述性能进行检测。同时对比未添加序列扰动、添加m序列扰动与添加Jacobi序列扰动所产生的三种跳频序列的性能。

2.1 序列均衡性和随机性检测

跳频序列的均衡性是衡量跳频序列中个频隙出现的次数的参数,理想跳频序列各频隙出现的次数应当相同,这样可以实现最大的处理增益。而随机性与均衡性类似,反映了跳频序列内部不同跳频码之间的统计相关特性,良好的随机性保证跳频码的不可递推。均衡性与随机性均可以用卡方检验的方法来进行统计。设序列长度为N,频隙数为q,每个频隙出现的次数为Ni(i=0,1,…,q-1)。

均衡性可以用下式进行计算:

令nij表示(xi,xi+e)在序列组合{(xi,xi+e)|xi、xi+e∈X,i=0,1,...,L-1}中累计出现的次数,其中e为一个自然数,通常取e=1,i+e的值遵从模N运算,ni*、nj*分别表示理想状态下每个频隙出现的次数。那么序列随机性可以用下式进行计算:

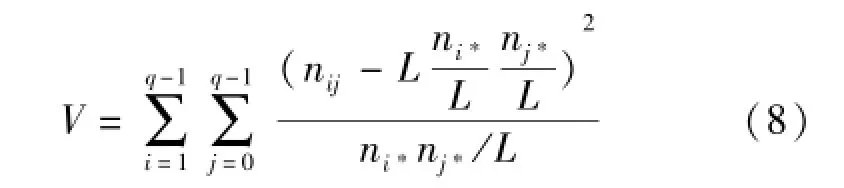
式(7)中用于计算均衡性的统计量服从χ2(q-1)分布,也称一维卡方统计,而式(8)中用于计算随机性的统计量服从χ2((q-1)2)分布,也称二维卡方统计。在置信度α=0.05的条件下,一维卡方检验的统计量理论参考值为82.53,二维卡方检验的统计量理论参考值为4 246.0。在序列长度为N=64 000,频隙q=64,初始迭代值为0.800 006的条件下序列的一维和二维卡方检验值如下表。

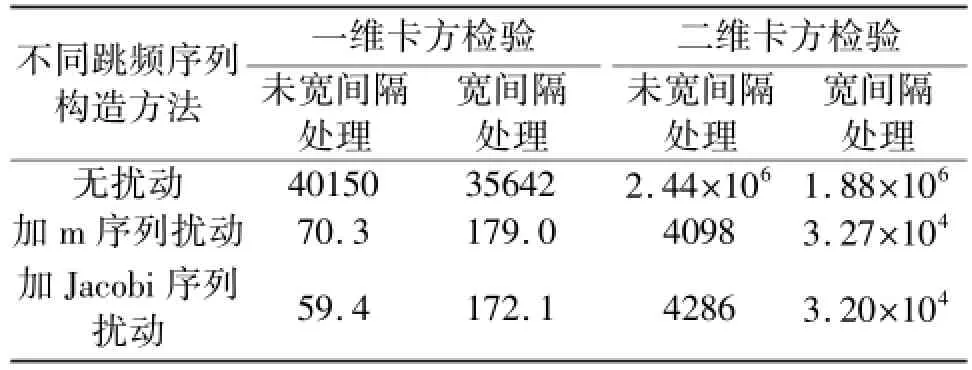
表1 置信度α=0.05时的一维、二维卡方检验值Table 1 Value of 1-demension and 2-dimension Chi-test with confidence level α=0.05

由上表可以看出,经过扰动之后序列的卡方检验值与理论参考值相相近,其性能明显优于未加扰动的混合混沌产生的序列。但是,经过宽间隔处理之后,序列的性能均下降,因此对序列进行宽间隔处理会降低序列性能。验证序列长度N=3 200、频系数q=64的条件之下,1 000个序列的卡方检验通过率,结果如表2所示。

表2 置信度α=0.05时的一维、二维卡方检验通过率Table 2 Passing ratio of 1-demension and 2-dimension Chi-test with confidence level α=0.05

由上表可以看出,未加扰动的级联混沌映射产生的跳频序列无论是否进行宽间隔处理,均衡性、随机性都未能通过检验。而添加扰动后,宽间隔处理只影响了序列的随机性检验,序列的均衡性得到了较好的保证,综上Jacobi序列扰动得到的跳频序列与m序列扰动的跳频序列在均衡性与随机性上差异不大。

2.2 序列汉明相关性检测

汉明相关性用来衡量跳频序列内部以及序列之间相互影响的程度,跳频序列的汉明相关性影响跳频多址组网的性能与对抗多径传播的能力。频隙数为q、长度为N的两个跳频序列X={xi}和Y={yj},在相对时延为τ时,非周期汉明相关定义为:

式中

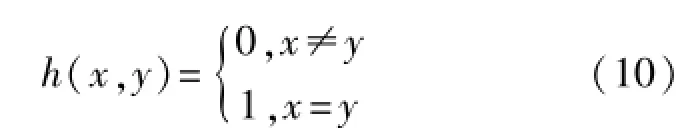
定义两个参量

分别表示跳频序列汉明自相关的最大旁瓣和汉明互相关的最大值,这两个参数与序列长度之比称作归一化汉明相关系数,分别用下式表示:

归一化汉明相关系数的理论参考值为

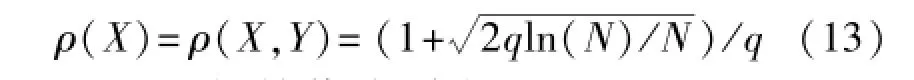
取q=64,初始值分别为0.800 006和0.800 007的条件下,计算不同长度序列的汉明相关系数,结果如图1和图2所示。

图1 频隙数为64,序列的汉明自相关特性Fig.1 Hamming auto-correlation of the sequence with 64 different frequencies

图2 频隙数为64,序列的汉明互相关特性Fig.2 Hamming cross correlation of the sequence with 64 different frequencies

由上图可以看出,Jacobi序列扰动得到的跳频序列的汉明相关性能与理论参考值接近,与m序列扰动得到的跳频序列的汉明相关性能接近,明显优于未经过扰动的跳频序列。

2.3 序列复杂性检测

序列复杂度是指跳频序列的复杂性水平,有限长序列的复杂度反映了其与真随机序列的相似程度。复杂度在一定范围内决定了跳频序列的抗破译能力和安全性能。文章采用文献[11]中提出的近似熵(ApEn,Approximate Entropy)准则衡量所产生序列的复杂度。图3是在序列长度为N=200的条件下,Ap-En随r值变化的曲线,图4是在r=1的条件下,不同序列长度的ApEn值。由图中曲线可以看出,Jacobi序列扰动得到的跳频序列的序列复杂度性能较好。

图3 ApEn随r值变化的曲线Fig.3 Curve of ApEn changing with the value of r

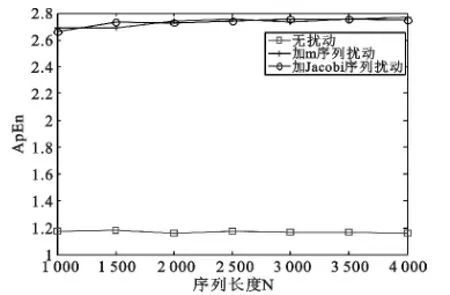
图4 不同序列长度的ApEn值Fig.4 ApEn value of sequence with various lengths

2.4 序列的平均间隔

序列X={xi}的跳频间隔定义为d=。跳频通信常希望跳频序列满足宽间隔跳频的要求,即相邻跳频时隙里发射的两个载波的频率间隔大于某特定值。具有宽间隔性能的跳频序列能有效应对阻塞式干扰和跟踪式干扰。因此,经常会对产生的初始跳频序列进行宽间隔处理。文章在选取q=64,初始值为0.800 006的条件下,将不同长度序列的跳频间隔进行了仿真计算,结果如图5所示。

由图5可以看出,经过宽间隔处理后的跳频序列其跳频间隔要明显大于未经宽间隔处理的,然而无扰动序列的宽间隔性能最好。因此,经过扰动之后的序列其跳频间隔性能略有下降,这也是说明了,为了获得均衡性、复杂性、汉明相关性等性能的提高,会使跳频间隔性能有所下降,但是依旧优于参考值。

图5 跳频序列跳频间隔Fig.5 Interval of the adjacent FH sequence

3 结 语

过上述仿真结果分析,文章所采用方法产生的跳频序列具有较好的均衡性,汉明相关性以及较大的复杂度和平均跳频间隔,能够满足跳频通信的要求。由于m序列的数量极其有限,且现有文献对m序列的研究与破译已趋于成熟。因此与添加m序列扰动产生的跳频序列相比,文章产生的跳频序列在数量与抗破译性上具有优势。另外,文章所采用算法更加适合于产生迭代式跳频序列,下一步将会研究如何对该算法进行必要的改善以适应实时性对于算法的要求。

[1] 梅文华,杨义先,周炯槃.跳频序列设计理论的研究进[J].通信学报,2003,24(02):92-101.

MEI Wen-hua,YANG Yi-xian,ZHOU Jiong-pan.Survey of Theoretical Bounds and Practical Constructions for Frequency Hopping Sequences[J].Journal of China Institute of Communications,2003,24(2):92-101.

[2] 胡雁,贺知明.混沌宽间隔跳频序列构造方法的比较[J].通信技术,2010,43(09):1-3.

HU Yan,HE Zhi-ming.Comparisons on Two Constructions of FH Sequences with Given Minimum Gap based on Chaos [J].Communications Technology,2010,43(09):1-3.

[3] 米良,朱中梁.一种基于Logistic映射的混沌跳频序列[J].电波科学学报,2004,19(03):333-337.

MI Liang,ZHUZhong-liang.ChaoticFrequency Hopping Sequences Based on Logistic Map[J].Chinese Journal of Radio Science,2004,19(3):333-337.

[4] 王喜风,王可人,金虎,基于Tent映射双向耦合映象格子的宽间隔跳频序列及其性能分析[J].电讯技术, 2011,51(05):17-22.

WANG Xi-feng,WANG Ke-ren,Jin Hu.Wide gap Frequency Hopping Sequences Based on Tent Double Coupled Map Lattice and Its Performance Analysis[J]. Telecommunication Engineering,2011,51(5):17-22.

[5] 张鸿儒.构造宽间隔跳频序列方法的研究[D].成都:西南交通大学,2011.

ZHANG Hong-ru.Research on Frequency-Hopping Sequence with Given Minimum Gap[D].Chengdu:Southwest Jiaotong University,2011.

[6] 张硕,张炜,高凯.一种混沌差分跳频序列的产生及性能分析[J].信息化研究,2010,36(02):16-18.

ZHANG Shuo,ZHANG Wei,GAO Kai.A Method to Generate Chaotic DFH Sequence and Its Performance Analysis [J].Informatization Research,2010,36(2):16-18.

[7] 刘金梅,张卫,丘水生,一种改善Tent混沌序列随机性的方法[J].计算机工程,2012,38(06):10-12.

LIU Jin-mei,ZHANG Wei,QIU Shui-sheng.Method for Improving Randomness of Chaotic Sequences[J].Computer Engineering,2012,38(6):10-12.

[8] 李文化,王智顺,何振亚.用于跳频多址通信的混沌跳频码[J].通信学报,1996,17(06):17-21.

LI Wen-hua,WANG Zhi-shun,He Zhen-ya.Chaotic FH Codes for FH-SSMA Communications[J].Journal of China Institute of Communications,1996,17(6):17-21.

[9] 张海艳.基于Legendre和Jacobi序列的研究[D].上海:上海交通大学,2011.

ZHANG Hai-yan.Research on Legendre and Jacobi Sequences[D].Shanghai:Shanghai Jiaotong University,2011.

[10] ZHANG Hua-qing.Design and Performance Analysis of Frequency Hopping Sequences with Given Minimum Gap [C]//International Conference on Microwave and Millimeter Wave Technology(ICMMT).China:IEEE Press, 2010:1271-1274.

[11] LI Zan,CAI Jue-ping,CHANG Yi-lin.Determining the Complexity of FH/SS Sequence by Approximate Entropy[J].IEEE Transactions on Communications, 2009,57(03):812-820.

MA Shi-wang(1989-),male,graduate student,mainly working at satellite FH communication.

陆锐敏(1963—),男,硕士,研究员,主要研究方向为卫星通信; LU Rui-min(1963-),male,M.Sci.,research fellow,mainly working at satellite communication.

赖 平(1989—),男,硕士,主要研究方向为卫星通信、扩频通信;

LAI-Ping(1989-),male,M.Sci.,mainly working at satellite communication and SSC.

张严平(1990—),男,硕士研究生,主要研究方向为卫星通信;

ZHANG Yan-ping(1990-),male,graduate student, mainly working at satellite communication.

Construction of Wide Interval Frequency-Hopping Sequence based on Improved Tent Chaotic Mapping

MA Shi-wang1,LU Rui-min2,LAI Ping3,ZHANG Yan-ping1
(1.Institute of Communication Engineering,PLA University of Science&Technology,Nanjing Jiangsu 21000,China; 2.Nanjing Telecommunication Technology Institute,Nanjing Jiangsu 21000,China; 3.Unit 63981of PLA,Wuhan Hubei 430311,China)

Frequency-hopping(FH)sequence is one of the key technologies for FH communications.FH sequence generated from chaotic mapping is now a frequently-used method.Aiming at the problem of weak ability in anti-prediction and limited precision caused by single mapping,Jacobi sequences is adopted to perturb the FH sequence generated from cascaded Logistic mapping and Tent mapping,then by using the algorithm of mod d plus remainder,the wide interval is processed.Simulation analysis indicates that the proposed FH sequence could fairly satisfy the requirements of FH communication in balance,randomness, Hamming correlation,complexity and average FH interval.

frequency-hopping sequence;wide interval;cascade mapping;sequences disturbance

TN918

A

1002-0802(2014)11-1271-05

10.3969/j.issn.1002-0802.2014.11.007

马世旺(1989—),男,硕士研究生,主要研究方向为卫星跳频通信;

2014-08-28;

2014-09-28 Received date：2014-08-28;Revised date：2014-09-28