DSSS系统频域干扰抑制算法的信噪比损耗分析*

李健伟,李志强,朱文明

(解放军理工大学通信工程学院,江苏南京210007)

DSSS系统频域干扰抑制算法的信噪比损耗分析*

李健伟,李志强,朱文明

(解放军理工大学通信工程学院,江苏南京210007)

以DSSS系统中频域干扰抑制算法为研究对象,针对干扰抑制模块的引入会给通信系统带来信噪比损耗的问题,首先介绍了频域干扰抑制技术的基本思想,其次重点分析了频域干扰抑制算法影响信噪比损耗的具体因素,主要包括窗函数类型、窗长度、加窗重叠度、阈值处理以及IFFT变换后的数据处理方式,然后对各个影响因素进行理论推导,并结合仿真分析,给出了各种情况下信噪比的损耗值,为干扰抑制算法的参数设计提供了依据。

DSSS 干扰抑制 加窗 阈值处理 信噪比损耗

0 引 言

DSSS是一种有效的抗干扰通信体制,在军事通信中一直备受重视,DSSS抗干扰[3]主要是利用扩频码的相关性在解扩时把不相关的干扰信号能量扩散,把相关的有用信号能量聚集。但由于处理增益[1-2]的限制,其抗干扰能力有限。当干扰信号很强时,仅靠对干扰信号进行能量扩散,会无法满足解扩解调器正常工作要求,对此有必要采取有效的干扰抑制技术提高系统的抗干扰能力。

常见的干扰抑制算法主要有时域预测技术[4]、变换域技术[5]和码辅助技术[6]。近年来,针对直接序列扩频干扰抑制技术有大量研究,其中频域抗干扰算法具有许多优点,被认为是一种极具潜力的抗干扰策略。频域干扰抑制技术利用直扩信号在频域上为白化的宽带功率谱,而窄带干扰信号功率谱占用频带很窄的特点,在接收端,将接收到的信号和干扰由时域变换到频域,检测出干扰的位置,按照设置的门限将受干扰的频带阈值处理,而后将信号反变换到时域进行解扩处理。频域干扰抑制算法能够有效抑制强干扰,但不可能彻底剔除干扰信号,且不可避免的会消掉部分有用信号,引起信噪比的损耗,因此干扰抑制算法的设计需要在剔除干扰和减小信噪比损耗之间折衷。

本文主要针对频域干扰抑制算法的信噪比损耗进行研究,首先对频域干扰抑制算法进行介绍,然后重点分析影响算法信噪比损耗的因素,主要包括窗函数类型、窗长度、加窗重叠度、阈值处理以及IFFT变换后的数据处理方式,最后通过理论推导结合仿真分析,得出各种因素对信噪比损耗的情况,为频域干扰抑制算法参数的最优设计提供了依据。

1 插损因素分析

频域干扰抑制技术[7]基本思想是对数字采样信号重叠加窗后进行FFT运算,把信号变换到频域,根据估计的背景噪声功率确定一个判决门限,大于门限的分量判为干扰信号,然后对变换域中的干扰信号分量进行修正,以消除干扰信号能量,再经过IFFT还原为时域信号。频域干扰抑制算法流程如图1所示。

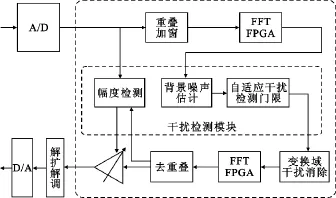
图1 频域干扰抑制算法流程Fig.1 Flow chart of frequency-domain interference suppression

由图1可看出,干扰抑制算法的处理步骤主要包括重叠加窗、FFT变换、背景噪声估计、干扰门限确定、干扰消除、IFFT变换和去重叠。

文献[8]对加窗做了详细分析,如果对接收到的信号不做加窗处理,直接进行N点的FFT运算,等效于加N点的矩形窗。矩形窗的第一旁瓣比主瓣低13 dB,即旁瓣抑制度只有-13 dB,对于干信比为几十dB的干扰,干扰的旁瓣仍然会污染整个信号频域。因而需要进行加窗处理,使主瓣聚集更多能量,同时旁瓣幅度减小。从时域上看,加窗就是对输入数据进行加权,窗函数系数从中心向两端逐渐衰减,保证数据段两端平滑,从而减小频谱泄漏。但由于窗函数向两端衰减,导致输入信号发生畸变,会带来额外的信噪比损失。

为了补偿加窗造成的信噪比损耗,需要对输入数据进行重叠加窗,文献[9]对重叠加窗技术进行了说明。重叠加窗后,需要考虑的是如何将干扰抑制后的两路数据合成一路作为最终的输出结果。目前主要有两种方法:选择法和相加法。以1/2重叠加窗为例,选择法的基本思想是取每路信号的窗口中心的1/2块的数据,舍弃左右两边各1/4块的数据,将上下两路1/2块的数据组成一个完整的数据序列。相加法则是将两段数据的重叠部分相加作为最终输出信号。重叠加窗以增加运算复杂度为代价,减小了加窗对信噪比的损耗。

在频域干扰消除子模块中,当检测到干扰频点后,就需要对干扰频点的幅值进行阈值处理[10],这个过程在处理干扰的同时会不可避免的对有用信号带来损耗,导致输出信噪比降低。

综合上述分析,影响干扰抑制算法信噪比损耗的主要因素有窗函数类型、窗长度、加窗重叠度、阈值处理以及IFFT变换后的数据处理。因此,如何设计算法参数使各种因素对输出信噪比损耗最小是值得研究的问题。

2 窗函数的损耗分析

假设x(k)是接收序列的样本序列,x(k)=Ap(k)+n(k),p(k)是等概率取值±1的PN码序列,其长度为N;n(k)为均值为零、方差为的高斯白噪声序列。A为信号幅度;对x(k)进行加窗处理,窗函数为w(k),加窗后的序列:

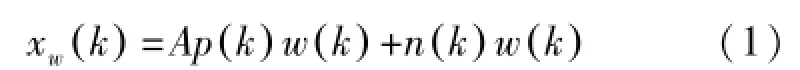
对xw(k)进行长度为N的相关解扩并积分得:

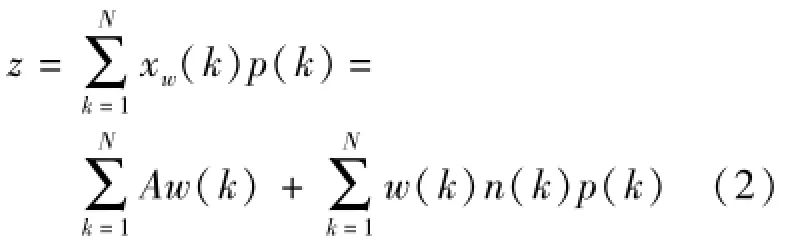
该序列的均值与方差:

由式(3)和式(4),可得加窗后的序列信噪比为:

不加窗的相关输出信噪比为:

由式(5)和式(6),可得加窗带来的信噪比损失为:

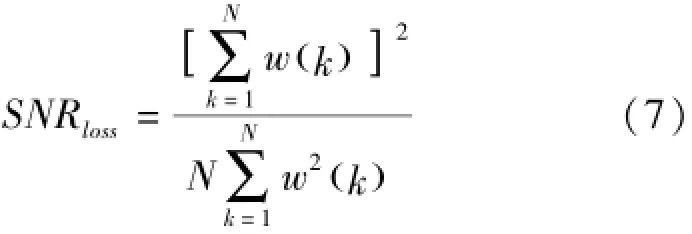
由式(7)可知,加窗引起的信噪比的损失主要由窗函数系数和窗函数点数决定。由式(7)计算,得出了当窗长度为1024时,常用几种窗函数的特性及其引起的信噪比损失,具体见表1。

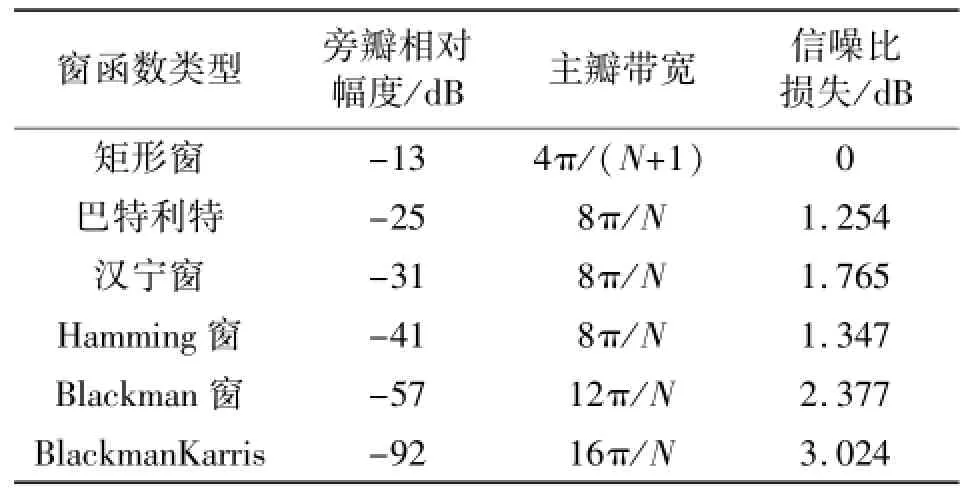
表1 窗函数基本特性及引起的信噪比损失Table 1 Basic characteristics of window function and SNR loss

3 加窗重叠度的损耗分析

假设加窗重叠因子是α,下面分析选择法和相加法重叠输出的信噪比损失。

选择法输出方式下,重叠加窗后的输出序列为:

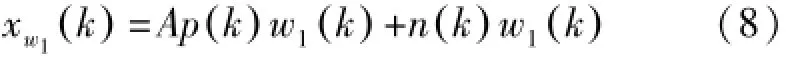
式中,w1(k)是选择法输出下的信号加权值:

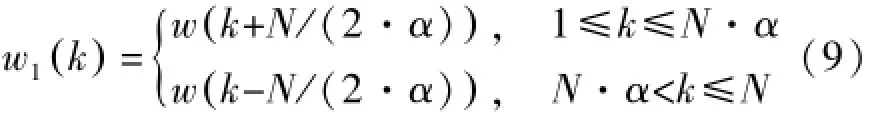
由信噪比损失的推导结果可知,选择法输出方式下的信噪比损失为:

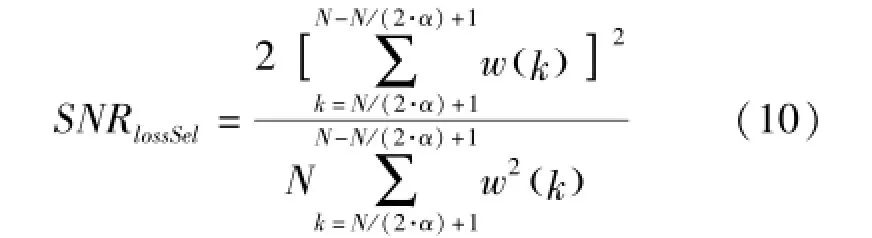
相加法输出方式下,重叠加窗后的输出序列为:

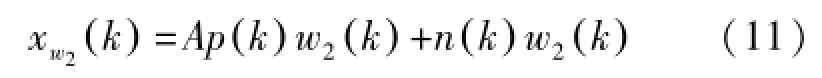
式中,w2(k)是相加法输出下的信号加权值:

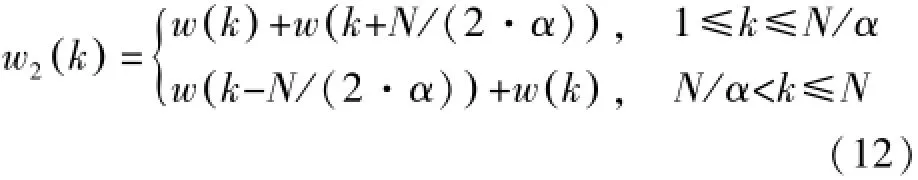
相加法的信噪比损失如下式:

由式(10)和式(13)可知,不同的加窗重叠度和输出数据处理方式对信噪比的损失不同。由式(10)和式(13)计算,得出了当窗长度为1 024时,对于各种窗函数的类型,不同的重叠因子下的选择输出和相加输出带来的信噪比损失情况,具体见表2。

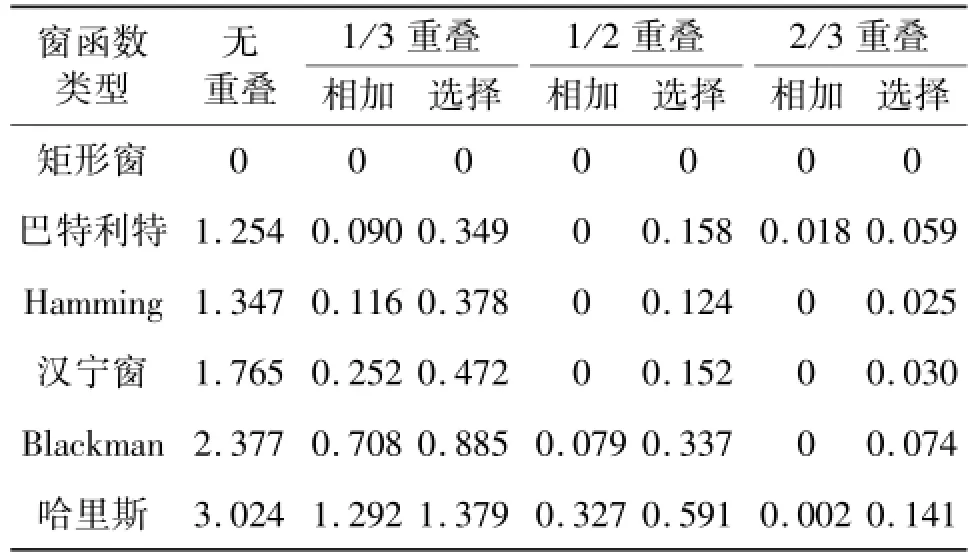
表2 两种数据合成方式不同重叠因子的信噪比损失Table 2 Different compound methods of two data and SNR loss

4 阈值处理损耗分析

检测到干扰频点后需要对谱线进行阈值处理,工程上常用的阈值处理算法主要有干扰归零算法、干扰钳位算法、干扰衰减算法。

(1)干扰归零法

算法基本思想是把幅度高于干扰消除门限的频谱分量归零,完全消除频点上的干扰能量,同时也消除了频点上扩频信号的能量,干扰归零算法对FFT变换后谱线做如下处理:

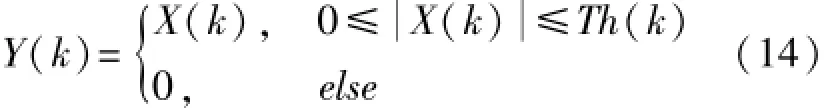
式中,Y(k)为干扰抑制后的频谱,经IFFT后输出信号为y(n),|X(k)|示离散谱线的模,Th(k)表示自适应的干扰门限阈值。

(2)干扰钳位算法

算法基本思想是使经过FFT变换后的频谱中干扰谱线的幅度保留在门限值Th(k)上,抑制了干扰谱线的大部分能量,同时保留了干扰谱线中扩频信号的相位信息。干扰钳位算法对FFT变换后谱线做如下处理:

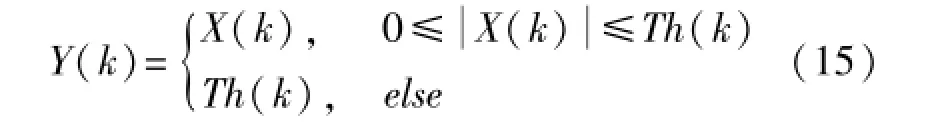
式中,Y(k)为干扰抑制后的频谱,|X(k)|示离散谱线的模,Th(k)表示自适应的干扰门限阈值。

(3)干扰衰减算法

算法基本思想是把确定为干扰的谱线按照一定比例进行衰减,使处理后的干扰谱线幅度与背景噪声相近,保持了该谱线的相位不变同时保留了部分扩频信号的能量,干扰衰减算法对FFT变换后谱线做如下处理:

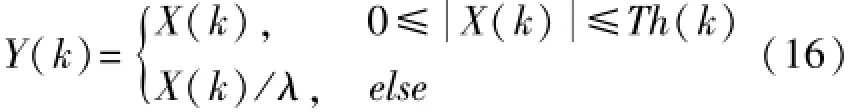
式中,Y(k)为干扰抑制后的频谱,|X(k)|示离散谱线的模,Th(k)表示自适应的干扰门限阈值,λ为衰减因子。

由上述分析可知,干扰归零算法、干扰钳位算法、干扰衰减算法在处理干扰的同时都不可避免的对信号带来了损耗,降低了输出信噪比。下面通过仿真分析比较各种算法的性能。

5 仿真分析

仿真一:假设信息速率为1 kbps,码片速率为1.024 Mcps,采样频率为10 Mhz,窗长度为1 024,仿真分析各种窗函数类型对信噪比损耗情况,仿真结果如图2所示。

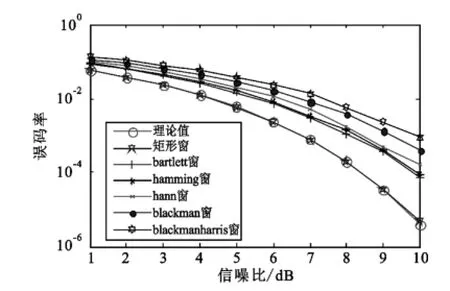
图2 各种窗函数在不同信噪比时的误码率Fig.2 Signal power vs.BER

由图2可知,不同的窗函数带来的信噪比损失不同,在窗长度一定时,对信噪比损失由大到小的窗函数依次是矩形窗、barllett窗、hamming窗、hann窗、blackman窗和blackmanharris窗。矩形窗的信噪比损失最小,主瓣最窄,但其相对旁瓣幅度最大;blackharris窗的信噪比损失最大,主瓣最宽,但其相对旁瓣幅度最小。旁瓣较低的窗函数可以将窄带干扰信号的大部分能量限定在有限的几根谱线之内,从而减少需要抑制的谱线的根数,最大程度地减小干扰对有用信号的影响,但旁瓣越低的窗函数,主瓣越宽,抑制窄带干扰的同时对有用信号的损伤也越大,因此,窗函数的选择应根据需要抵抗的干扰指标确定,选取既能达到抗干扰指标又能使信噪比损失最小的窗函数。

仿真二:假设信息速率为1 kbps,码片速率为1.024 Mcps,采样频率为10 Mhz,窗长度为1 024,加Blackman窗,仿真分析加窗重叠度和数据输出方式对信噪比损耗情况,仿真结果如图3和图4所示。

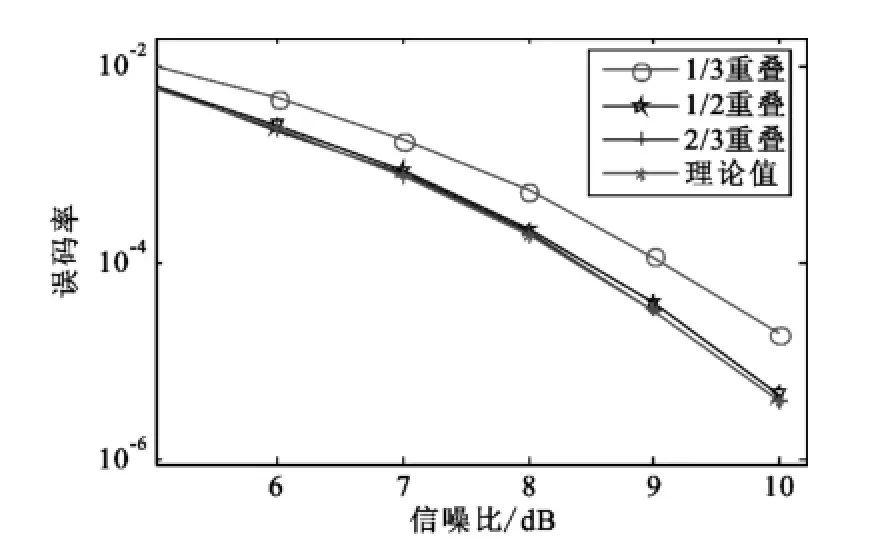
图3 相加输出时各种重叠因子在不同信噪比时的误码率Fig.3 Signal power vs.BER

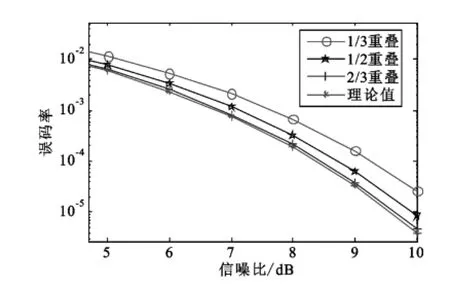
图4 选择输出时各种重叠因子在不同信噪比时的误码率Fig.4 Signal power vs.BER

由图3和图4比较分析可知,以Blackman窗作为研究对象,IFFT后的两路数据采取相加法的信噪比损耗要比选择法小,同时,加窗重叠比例越大,引入的加窗损耗越小,但相应的运算量越大,因此,加窗重叠比例应根据算法性能指标和硬件资源要求进行折衷选取。

仿真三:假设信息速率为1 kbps,码片速率为1.024 Mcps,采样频率为10 Mhz,窗长度为1 024,加Blackman窗,仿真分析阈值处理对信噪比损耗的影响情况,仿真结果如图5所示。

图5 各种阈值算法在不同干信比时的误码率Fig.5 Interference power vs.BER

由图5可知,在相同的参数设置条件下,干扰归零法、干扰钳位法、干扰衰减法对信噪比的损耗依次减小。干扰归零法在消除干扰的同时将该频点的信号一并滤除,对信号信噪比损失最大,同时也完全消除了干扰频谱上有用信号的相位信息,不利于后续捕获跟踪,但算法硬件实现简单;干扰钳位法将干扰频点的幅度陷为门限值,保留了部分有用信号能量和相位信息,对信号信噪比损失较小;干扰衰减法把干扰谱线按照一定比例进行衰减,使处理后的干扰谱线幅度与背景噪声相近,保持了该谱线的相位不变同时保留了部分扩频信号的能量,对信号信噪比损失最小,但该算法硬件实现复杂度高。

6 结 语

影响干扰抑制算法信噪比损耗的主要因素有窗函数类型、窗长度、加窗重叠度、阈值处理以及IFFT变换后的数据处理。由于窗函数的旁瓣相对幅度低时主瓣带宽更宽,需要处理的频点更多,而主瓣带宽窄时旁瓣相对幅度高,频谱泄露严重,被污染的频点更多,在选择窗函数时,要考虑接收信号的动态范围以及需要抑制的窄带干扰强度,选择合适的窗函数,减小对信噪比的损耗;加窗重叠比例越大,对信噪比损耗越小,但实现复杂度大和硬件资源消耗多,需要折中考虑;对于干扰频点阈值处理,干扰衰减法虽然效果优于干扰钳位法和干扰归零法,但实现复杂且会占用过多的运算资源,一般采用干扰钳位法;IFFT变换后的数据处理,一般情况下,相加法较选择法对信噪比的损耗更小,实际应用中更多采用相加法。

[1] POISEL A.Modern Communications Jamming Principles and Techniques-Richard[M]Beijing:Publishing House of Electronics Industry,2005:91-102.

[2] 查光明,熊贤祚.扩频通信[M].西安:西安电子科技出版社,2003:6-63.

CHA Guang-ming,XIONG Xian-zhe.Spread Spectrum Communication[M].Xi'an:Xi'an Electronic Science and Technology Press,2003:6-63.

[3] 李博,肖立民.基于最大输出信噪比的自适应置零陷波干扰抑制算法[J],通信技术,2010,43(04):46-49.

LI Bo,XIAO Li-ming.Adaptive Zero-set Interference suppression Algorithm Based on Maximal SNR Output[J], Communications Technology,2010,43(04):46-49.

[4] MASRY E.Closed-form Analytical Results for the Rejection of Narrow-band Interference in PN Spread Spectrum Systems-Part:Linear Prediction Filter[J].IEEE Transaction on Communication,1985,33(01):10-19.

[5] SAULNIER G J.Suppression of Narrowband Jammers in aSpread Spectrum Receiver Using Transform Domain A-daptive Filtering[J].IEEE Journal on Selected Areas in Communication,1992,10(04):742-749.

[6] VINCENT P.H..Code-Aided Adaptive Narrow-Band Interference Suppression for Direct Sequence Spread Spectrum Communications[J].IEEE Military Communications Conference,1997(02):575-579.

[7] YONG J A,LEHNERT J S.Analysis of DFT-based Frequency Excision algorithms for direct-sequence spreadspectrum Communications[J].IEEE Transactions on Communications,1998,5(03):203-217.

[8] 曾祥华,李峥嵘,王飞雪.扩频系统频域窄带干扰抑制算法的加窗损耗研究[J].电子与信息学报,2004,26 (08):1276-1281.

CENG Xiang-hua,LI Zheng-rong,WANG Fei-xue. The Frequency Domain Narrowband Interference Suppression Algorithm for Spread Spectrum System[J].Journal of Electronics&Information Technology,2004,26(08): 1276-1281.

[9] 王坚,刘伟,柳彦.一种基于加窗的窄带干扰抑制技术仿真与硬件实现[J].电讯技术,2008,48(01):82-85.

WANG Jian,LIU Wei,LIU Yan.A Window-based Narrow Band Interference Suppression Technology Simulation and Hardware Implementation[J].Telecommunication Technology,2008,48(01):82-85.

[10] 王世练,邬书跃.DS/FH中窄带干扰的变换域处理方法研究[J].国防科技大学学报.2001,23(04):98-101.

WANG Shi-lian,WU Shu-yue.Method of Transform Domain Narrowband Interference on DS/FH[J].Journal of National University of Defense Technology,2001,23 (04):98-101.

Li Jian-wei(1990-),male,graduate student,majoring in satellite communications.

李志强(1974—),男,博士,教授,主要研究方向为卫星通信;

Li Zhi-qiang(1974-),male,Ph.D., professor,majoring in satellite communications.

朱文明(1979—),男,博士,讲师,主要研究方向为卫星通信。

Zhu Wen-ming(1979-),male,Ph.D.,lecturer,majoring in satellite communications.

SNR-Loss Analysis of Frequency Domain Interference Suppression Algorithm in DSSS System

LI Jian-wei,LI Zhi-qiang,ZHU Wen-ming
(Institute of Communications Engineering,PLA University of Science and Technology,Nanjing Jiangsu 210007,China)

With frequency domain interference suppression algorithm in DSSS system as the research object,and aiming at the problem that the introduction of interference suppression module would result in SNR loss in communication system,this paper firstly describes the basic idea of frequency domain interference suppression,then principally analyzes the specific factors of SNR loss affected by the algorithm,including the types of window function,window length,window overlap,threshold processing and data processing method after IFFT transformation,and then provides the theoretical derivation of each affecting factors.Finally,in combination of simulation analysis,the paper gives the value of SNR loss and provides a reference for the design of interference suppression algorithm.

DSSS;interference suppression;windowing;threshold processing;SNR loss

TN91

A

1002-0802(2014)11-1266-05

10.3969/j.issn.1002-0802.2014.11.006

李健伟(1990—),男,硕士研究生,主要研究方向为卫星通信;

2014-08-21;

2014-10-13 Received date：2014-08-21;Revised date：2014-10-13

国家自然科学基金(No.61032004,No.91338201);国家高技术研究发展计划(“863”计划)(No.2012AA121605,No.2012AA01A510)

Foundation Item：National Natural Science Foundation of China(No.61032004,No.91338201);The National High Technology Research and Development Program(“863”program)(No.2012AA121605,No.2012AA01A510)