二维MMSE信道估计算法研究与FPGA实现*

梁 尧,周明宇,何 丽

(1.深圳空天通信终端应用技术工程实验室,广东深圳518057; 2.哈尔滨工业大学电子与信息工程学院,黑龙江哈尔滨150006; 3.深圳市无线宽带信号传输与处理技术重点实验室,广东深圳518057)

二维MMSE信道估计算法研究与FPGA实现*

梁 尧1,2,周明宇3,何 丽1

(1.深圳空天通信终端应用技术工程实验室,广东深圳518057; 2.哈尔滨工业大学电子与信息工程学院,黑龙江哈尔滨150006; 3.深圳市无线宽带信号传输与处理技术重点实验室,广东深圳518057)

OFDM把宽带频率选择性衰落划分为多个窄带平坦衰落,能有效地对抗衰落信道符号间干扰,广泛应用于数字电视、无线局域网以及4G移动通信领域。信道估计作为OFDM关键技术之一,针对给定信道的最大多普勒频移、最大多径时延条件下,利用二维MMSE算法设计最优导频图案以及维纳滤波插值阶数,并且在FPGA中进行实现。与常规二维维纳滤波相比,其具有硬件复杂度低,接近理想估计性能的特点,具有一定的工程参考和应用价值。

OFDM 二维MMSE 信道估计 FPGA

0 引 言

正交频分复用技术[1]把宽带频率选择性衰落划分为多个窄带平坦衰落,能有效地对抗衰落信道多径引起的符号间干扰,广泛应用于数字电视、无线局域网以及4G移动通信领域[2]。信道估计作为OFDM关键技术之一,其估计精度是影响整个系统误码性能的重要参数。本文讨论给定信道先验知识最大多普勒频移fDmax、最大多径时延τmax下,如何合理设计OFDM的训练序列(导频)和决定维纳滤波插值阶数,以及根据导频图案和信道统计特性计算二维Wiener[3]滤波插值矩阵,简化成硬件可实现的LMMSE信道估计等问题。最终在FPGA中利用本文的设计方法和仿真得到的最优解,实现了LMMSE信道估计,进一步验证了本方案的可行性。

1 MMSE信道估计原理

文献[4]给出了LS即最小平方意义下的信道估计方法:

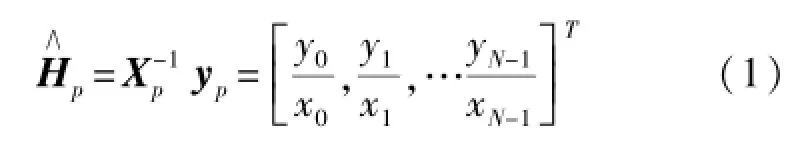
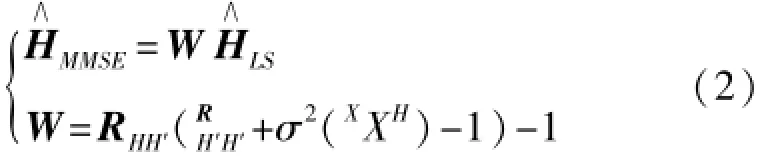
式中W为Wiener滤波插值矩阵,RH′H′为导频间的自协方差矩阵,RHH′为导频与信号子载波之间的互协方差矩阵。为避免W随输入信号X变化而变化,取E{(XXH)-1}代替(XXH)-1,式2进一步化简为:

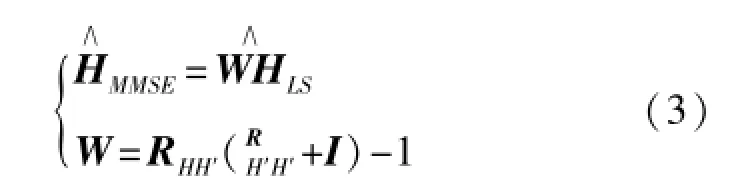
2 信道相关矩阵的求解

式(3)只是从理论给出了计算LMMSE信道估计方法,具体工程实现时需要针对不同的信道环境对信道相关矩阵RH′H′与RH′H进行求解。文献[6]给出了信道的时频二维相关矩阵具有在频域与时域统计特性的相互独立性,利用这一特性可将原来二维Wiener滤波插值转化为频域与时域两个独立的一维Wiener滤波插值过程。

在已知信道最大多径τmax下,利用信道的时延功率谱密度[6-8]

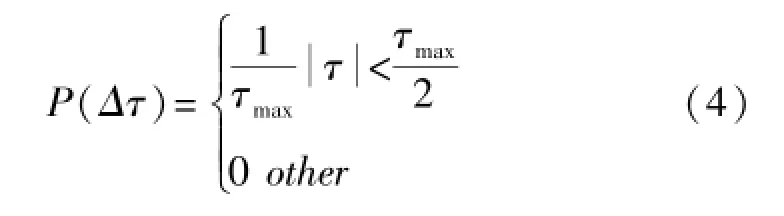
可以计算离散频率互相关函数:

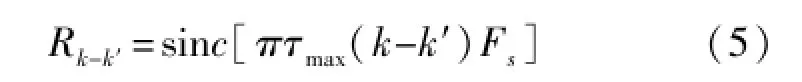
式中Fs为系统采样频率。

在已知信道最大多普率频移fDmax下,利用信道多普勒谱[6-8]

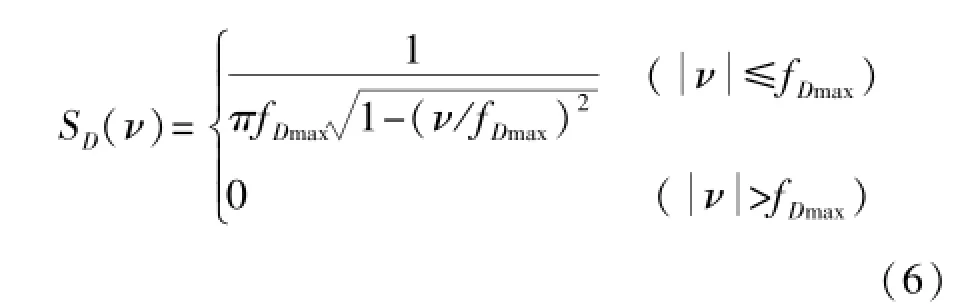
可以计算离散时域互相关函数:

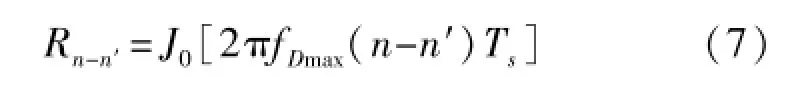
式中Ts为一个OFDM符号(包含CP)的周期。

以频域插值滤波为例,在已知最大多径时延τmax,频域导频间隔n,以及频域插值滤波阶数p,进行维纳滤波插值的信道估计过程,等价于利用相邻位置已知的p个导频信息(利用LS信道估计获得),通过n倍插值,还原得到n-1个信道估计信息以及对其中1个导频位置的信道估计进行修正。因此,计算信道相关矩阵RH′H′与RH′H的过程,即为根据n个待插值位置信息,以及相邻的p个导频位置信息,利用式(5)计算可以得到n×p阶互协方差矩阵RH′H。根据p个导频位置信息,用式(5)计算可以得到p×p阶导频自协方差矩阵RH′H′

同理,已知最大多普勒频移fDmax,时域导频间隔m,以及时域插值滤波阶数q,利用式(7)可计算得到时域信道相关矩阵RH′H′与RH′H。

分别将频域和时域计算的信道相关信息RH′H′与RH′H,代入式(3)即可分别完成时频二维LMMSE信道估计过程。

3 导频设计与LMMSE性能仿真

上文推导给出了计算LMMSE信道估计方法,以及信道相关矩阵RH′H′与RH′H计算方法,余下的问题是导频插入间隔以及Wiener滤波抽头数的选取问题。特别是在工程实现时需要在系统性能与硬件资源利用之间做出平衡。不失一般性,本文在给定如表1所示系统参数后,对不同导频插入间隔、不同插值滤波抽头数进行仿真,最终确定最优解。

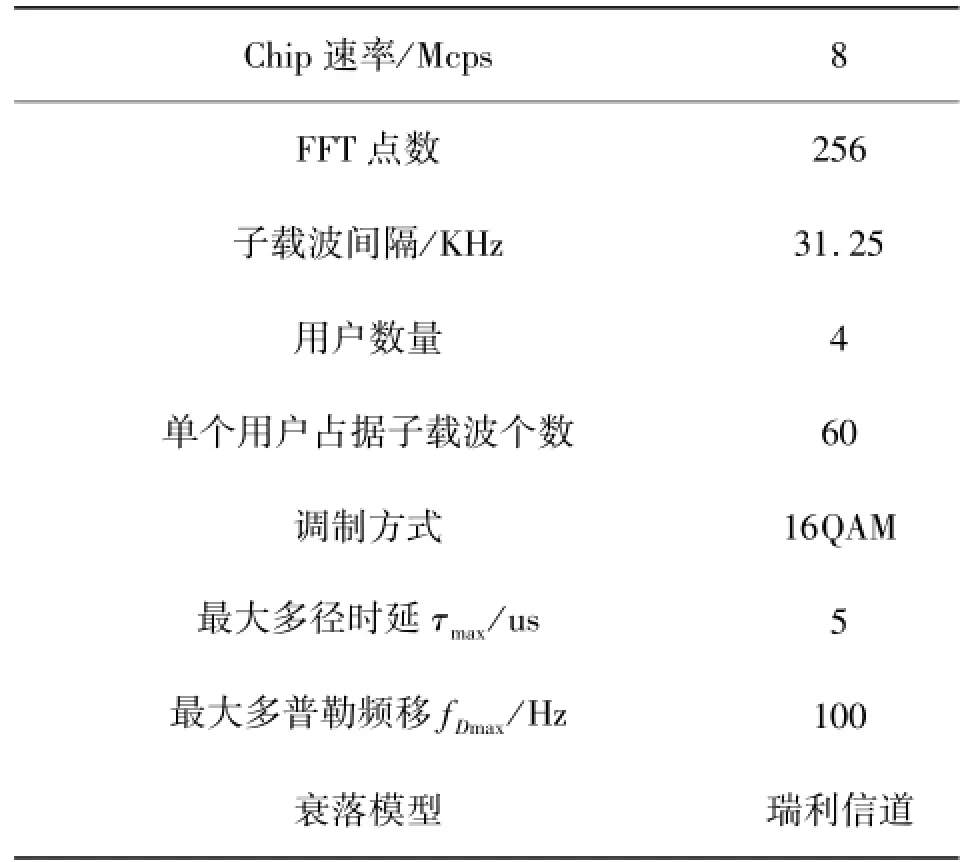
表1 OFDMA系统参数Table 1 Parameters of OFDMA system

3.1 导频的时频域间隔选取与性能仿真

根据二维Nyquist采样定理,导频间隔需满足相干时间与相干带宽的限制[9]:

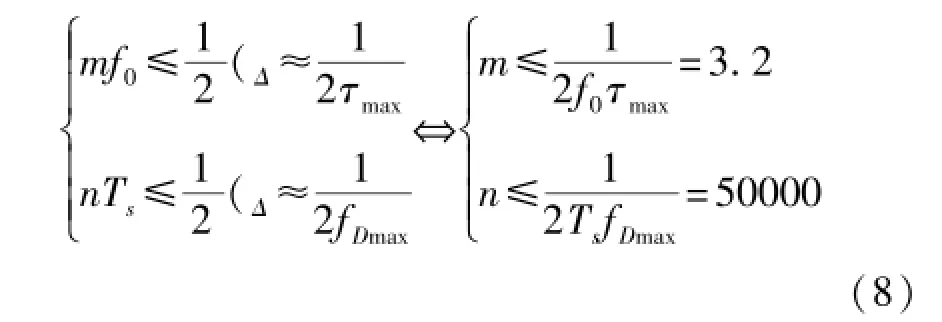
式中m表示频域导频间隔,n表示时域导频间隔,f0为子载波的间距,Ts为单个OFDM符号的持续时间。固定Wiener滤波器阶数p=q=7,针对不同导频插入间隔m×n,采用LMMSE算法仿真结果如图1所示。当m=n=5时,明显不满足式(8),因此通过Wiener滤波恢复的信道估计结果与理想值存在很大的偏差。取m=n=3时,满足式(8),LMMSE仿真结果已经非常接近理想信道估计,可取其作为本系统的最优导频间隔。

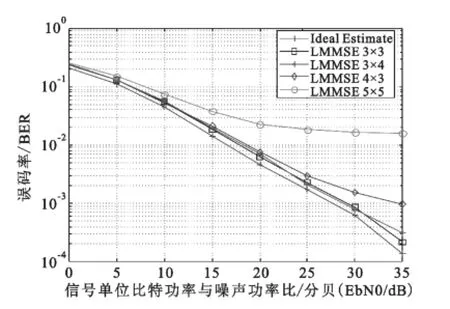
图1 16QAM在不同插值间隔下LMMSE误码性能Fig.1 Performance for different pilot patterns based on 16QAM LMMSE

3.2 不同Wiener滤波器阶数对MMSE性能影响

理论上Wiener滤波抽头越高,系统可利用的信道相关信息就越多,信道估计结果越精准,但硬件计算消耗的复数乘法器也将越多。根据3.1仿真得到的导频插值最优解m=n=3,针对不同的时域和频域Wiener滤波器抽头数p×q,其中p表示频域滤波抽头数,q表示时域频域滤波抽头数,仿真得到误码性能曲线如图2所示。当p=q=3时,在Eb/N0＞20 dB时,误码曲线将出现平顶,原因是此时信道相关信息已经利用到极限,无法再通过LMMSE插值获得增益;当p=q=5时,LMMSE仿真结果非常接近理想信道估计性能,可作为本系统最优滤波抽头数解。

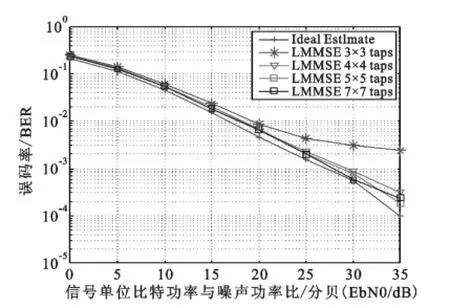
图2 16QAM在不同Wiener滤波阶数下LMMSE误码性能Fig.2 Performance for different wiener filtering taps based on 16QAM LMMSE

3.3 不同调制方式下系统性能

根据前面两个仿真结果,在系统性能与硬件资源利用率间作出平衡,决定选取块状导频方式,并且频域导频间隔为3,时域为3,时域插值滤波抽头数为5,频域抽头数为5作为本系统最优解。针对不同调制方式,采用LMMSE算法仿真得到误码率曲线如图3所示,系统的MSE曲线如图4所示。仿真结果显示本设计的导频和滤波抽头数,采用LMMSE估计,在不同调试方式下均接近理想信道估计的性能,具有很大的鲁棒性。

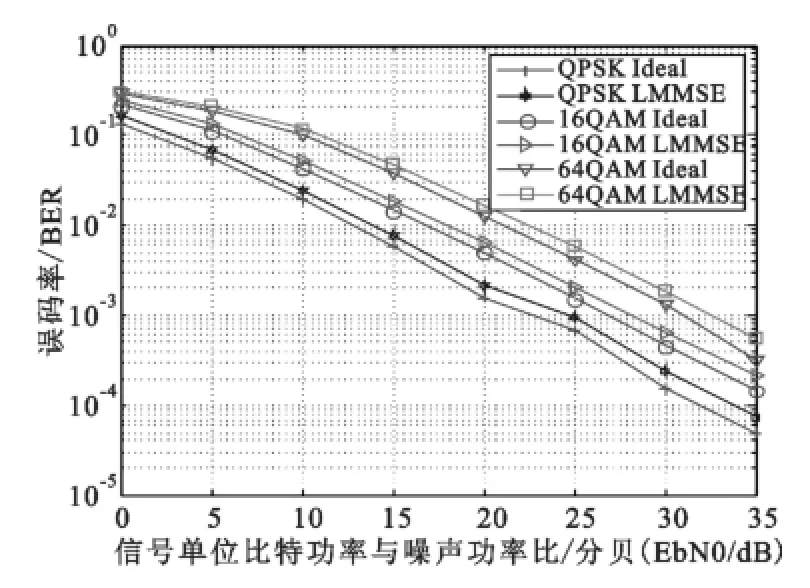
图3 不同调制方式下LMMSE误码率曲线Fig.3 Performance for different modulations base on LMMSE

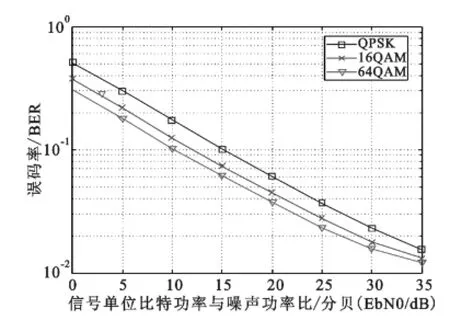
图4 不同调制方式下LMMSE估计值的均方误差曲线Fig.4 MSE for different modulations based on LMMSE

3.4 信噪比SNR不匹配对MMSE性能影响

观察式子(3)中维纳滤波插值矩阵W的计算,其中,时域信道相关矩阵RH′H′与RH′H由导频位置与插值滤波器阶数决定,可以视为常量;β为信号的平均能量,由调制方式决定,实现上通常将能量归一化为1。剩下的只有信噪比SNR为变量。真实的通信非扩频高阶调制系统通常SNR＞0 dB。图5为固定几种不同的信噪比,利用式(3)对维纳滤波插值矩阵W进行计算,最终得到16QAM下信噪比SNR不匹配对MMSE性能影响。

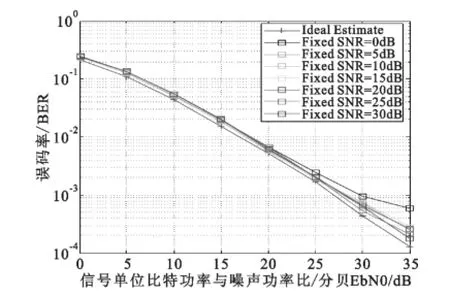
图5 16QAM在SNR不匹配下的性能Fig.5 Performance oncalculatingWwith unmatched SNR

从图5可以看出,信噪比不匹配对系统误码率的影响不大,硬件实现时为了避免矩阵求逆,降低硬件复杂度,可固定一个SNR=15 dB,此时W可视为常量,直接通过在Matlab中脱机将其计算得到,并保存到硬件的ROM中,作为硬件的计算结果。

4 LMMSE信道估计FPGA硬件实现

4.1 LMMSE硬件系统架构

利用3.4的结论,为了避免矩阵求逆,降低硬件复杂度,首先在软件Matlab中利用式(3)、式(5)、式(7),固定一个SNR=15 dB计算出频域插值矩阵FreqCoff和时域插值矩阵TimeCoff。然后,将插值系数矩阵FreqCoff和TimeCoff存入FPGA中RAM中,作为Wiener滤波器抽头矩阵。LMMSE信道估计在硬件中实现过程最终等效为提取特定位置导频信息作为行向量分别与插值矩阵FreqCoff和TimeCoff中特定的列向量相乘(卷积滤波)过程,硬件系统架构如图6所示。

图6 LMMSE硬件FPGA实现架构Fig.6 Architecture of LMMSE hardware implementation based on FPGA

如图6,根据导频表RAM内容将经过FFT的频域信号进行提取,分别获得用户导频和用户数据。然后,对提取到的导频分别进行频域和时域插值滤波即可得到LMMSE信道估计结果,再进行重新排序。同时,另一路用户数据经过硬件延迟后,与其对应的LMMSE结果进行复数域相除,最终得到MMSE均衡结果。详细的频域插值滤波过程如图7所示,

图7 频域Wiener插值滤波器硬件实现流程Fig.7 Flow diagram of frequency domain wiener interpolation filters in FPGA for LMMSE

时域插值过程与频域插值滤波过程同理。其中,频域插值过程根据插入位置样式的不同分为头部、中间、尾部3个部分,并且都是通过找出对应位置的插值滤波抽头系数与导频数据进行卷积过程,最终对数据进行重新的整理,输出插值滤波结果,并且产生相应的帧同步和数据使能信息。

4.2 LMMSE硬件仿真结果分析

根据表1给定的OFDMA系统参数,结合前面仿真得到最优解:频域导频间隔为3,时域为3,时域插值滤波抽头数为5,频域抽头数为5,在FPGA中编写Verilog代码,并利用Modelsim进行时序仿真得到结果如图8所示。从硬件仿真图可以大概看出,经过LMMSE均衡后的IQ数据明显更加集中在正负几个取值。这说明硬件均衡后结果大致收敛为星座图上映射的若干个点。

图8 LMMSE硬件时序仿真Fig.8 Simulation chart for LMMSE in FPGA

进一步将FPGA硬件处理数据导入到Matlab中进行分析。最终得到无LMMSE均衡的16QAM星座图如图9所示,经过LMMSE均衡的星座图如图10所示。明显经过硬件LMMSE均衡后,星座图的点分布更加集中,系统误码率得到了极大的改善。

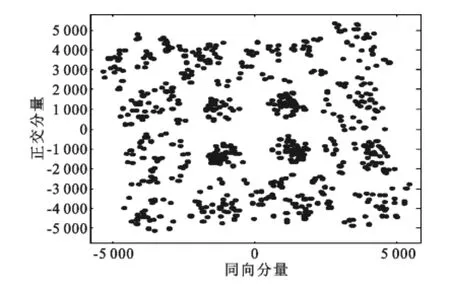
图9 不经过信道估计的16QAM星座图Fig.9 16QAM constellation without LMMSE

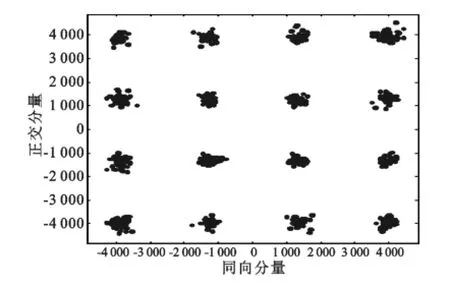
图10 经过FPGA硬件LMMSE信道估计的16QAM星座图Fig.10 16QAM constellation after LMMSE in FPGA

5 结 语

本文从MMSE信道估计基本原理出发,围绕信道相关矩阵求解问题,研究在给定OFDM系统信道先验知识最大多普勒频移fDmax、最大多径时延τmax条件下,通过理论推导和仿真得到OFDM导频的时频域插值间隔以及插值滤波器抽头数的最优解。然后利用最优导频间隔和插值抽头数计算时域和频域滤波矩阵,并将其导入硬件中,最终在FPGA中实现了LMMSE过程。该设计具有硬件复杂度低、信道估计精度接近理想估计性能的特点,具有一定的理论参考和工程应用价值。

[1] 程履帮.OFDM系统中基于LMMSE信道估计算法的改进及其性能分析[J].电子学报,2006,36(09): 1782-1785.

CHENG Lv-bang,An Improved LMMSE Channel Estimation Method and Its Performance[J].Acta Electronica Sinica,China,Sep 2006,36(9):1782-1785.

[2] 张建康,穆晓敏,陈恩庆等.OFDM系统基于导频的信道估计算法分析[J].通信技术,2009,8(42):91-98.

ZHANG Jian-kang,MU Xiao-min,CHEN En-qing.Pilot-based Channel Estimation Algorithms for OFDM System[J].Communications Technology,2009,8(42): 91-98.

[3] WIENER N.The Wiener RMS(Root Mean Square)Error Criterion in Filter Design and Prediction[M].Edition 1.America:MIT Press,1949:129-48.

[4] YANG Lihua.Novel Noise Reduction Algorithm for LS Channel Estimation in OFDM System with Frequency SelectiveChannels[C]//CommunicationSystems (ICCS).Singapore:IEEE,2010:478-482.

[5] MOON.J and CHOI S.Performance of Channel Estimation Methods for OFDM Systems in A Multiple Fading Channels[J].IEEE Transactions on Consumer Electronics,2000,46(01):161-170.

[6] HASHEMI.H.Impulse Response Modeling of Indoor Radio Propagation Channels Selected Areas in Communication[J].IEEE Journal,1993,11(07):967-978.

[7] REESJ.V..Measurements of the Wide-band Radio Channel Characteristics for Rural,Residential,and Suburban Areas.[J]IEEE Trans on Vehicular Technology,1987,36(01):2-6.

[8] CULLENP.J.,P.C.Fannin and A.Molina.Wide-band Measurement and Analysis Techniques for the Mobile Radio Channel[J].IEEE Trans on Vehicular Technology, 1993,42(04):589-603.

[9] 张丽,匡麟玲,倪祖耀,等.单载波频域均衡中的二维MMSE信道估计[J].清华大学学报:自然科学版, 2010,50(10):1680-1683.

ZHANGLi,KUANG Lin-ling,NI Zu-yao,LU Jianhua.Two Dimensional MMSE Channel Estimation for Single-carrier Frequency Equalization[J].Tsinghua University:Sci&Tech,2010,50(10):1680-1683.

LIANG Yao(1984-),male,M.Sci.,engineer,majoring in wireless communication algorithm and FPGA hardware development.

周明宇(1987—),男,硕士,工程师,主要研究方向为无线通信算法及FPGA硬件实现;

ZHOU Ming-yu(1987-),male,M.Sci.,engineer,majoring in wireless communication algorithm and FPGA hardware development.

何 丽(1986—),女,硕士,工程师,主要研究方向为无线通信及嵌入式系统。

HE Li(1986-),female,M.Sci,engineer,majoring in wireless communication and embedded system..

2D MMSE Channel Estimation Algorithm and FPGA Implementation

LIANG Yao1,2,ZHOU Ming-yu3,HE Li1
(1.Shenzhen Engineering Laboratory of Aerospace Communication Endpoint Application Technology, Shenzhen Guangdong 518057,China;2.School of Electronics and Information Engineering,Harbin Institute of Technology,Harbin Heilongjiang 150006,China;3.Shenzhen Key Laboratory of Wireless Broadband Communication and Signal Processing,Shenzhen Guangdong 518057,China)

OFDM technology divides the broadband frequency selective fading channel into several narrowband flat fading channels,and this may efficiently resist the inter-symbol interference of fading channel. This technology is widely used in the field of digital TV,wireless local area network and 4G mobile communications.Channel estimation is a key technology of OFDM(Orthogonal Frequency Division Multiplexing).Aiming at the maximum Doppler frequency and maximum multipath delay of given channel and with 2D MMSE algorithm an optimal pilot pattern and Wiener filtering taps is designed,and implemented in FPGA.Compared with regular 2D Wiener filtering,it enjoys the characteristic of low complexity in hardware and approaches the ideal estimation performance,and thus is of certain engineering reference and application value.

OFDM;2D MMSE;channel estimation;FPGA

TN929.5

A

1002-0802(2014)11-1249-06

10.3969/j.issn.1002-0802.2014.11.003

梁 尧(1984—),男,硕士,工程师,主要研究方向为无线通信算法及FPGA硬件开发;

2014-07-02;

2014-09-17 Received date：2014-07-02;Revised date：2014-09-17