非对称视角下我国通货膨胀的动态行为分析

聂飒

（云南民族大学经济学院，云南 昆明 650031）

非对称视角下我国通货膨胀的动态行为分析

聂飒

（云南民族大学经济学院，云南 昆明 650031）

该文在非对称性视角下构建分位数自回归模型，实证检验我国1990年1月到2013年5月的月度通货膨胀率的动态发展趋势，研究得出，在较低的分位区间里，通货膨胀受到一个负向冲击以后便可调整到一个稳定水平，而在较高的分位区间里，通货膨胀受到一个正向冲击以后便表现为一个单位根过程，这说明通货膨胀的动态调整行为具有非对称性。另外，考虑到结构断点来重新估计模型可知，从总体来看通货膨胀的动态行为是一个平稳过程，但在不同的时期里通货膨胀的动态行为仍具有非对称性。上述实证检验结果可为国家出台治理通货膨胀、促进物价稳定的宏观调控政策提供现实依据。

通货膨胀；非对称视角；动态行为；分位数自回归模型

URI：http://www.cnki.net/kcms/detail/65.1210.C.20141121.1555.009.html

【经济研究】

中国自改革开放以来经历了多次通货膨胀过程，由于剧烈的通胀现象不利于宏观经济的稳定发展，于是国家逐渐把保持较低的通货膨胀水平或促进物价水平平稳提升作为国家宏观调控的主要目标之一。近十几年来，通货膨胀在许多宏观经济模型中发挥着十分重要的作用，通货膨胀的持久性成为货币政策的间接后果，于是了解通货膨胀持久性的类型以及决定因素对于经济学家和政策制定者来说就变得极为重要。通货膨胀的持久性是指通货膨胀受到一个冲击以后缓慢地收敛于其长期水平的趋势。当收敛于均衡水平的速度很低时，说明通货膨胀具有持久性。反之，当这种速度很快时，说明通货膨胀是不持久的。有很多因素可能会导致这种调整速度的下降，例如通胀预期、相对价格调整、工资指数化、货币与汇率政策等（Ozcan et al.，2004）[1]。与通货膨胀的动态性相关，本文的主要目的就是了解通货膨胀对于不同冲击的反应而做出动态变化的速度及形式。为了分析这种通货膨胀的动态行为，目前实证研究中一般使用的是单位根检验方法、向量自回归模型（VAR）以及误差修正模型（ECM），上述方法基本潜含着以下两个假设：一是不管通货膨胀是高于或低于其稳定状态水平，也不管其受到的冲击大小及方向，通货膨胀这种向其均衡状态变化的速度是不变的；另一个假设是通货膨胀变量分布是正态分布。上述两个假设存在以下问题，第一个假设仅是将通货膨胀过程分为单位根过程和平稳过程，这就阻碍了对于通货膨胀动态性的进一步探索；第二个假设则是由于异常值的存在，通货膨胀率并不总是呈正态分布，因此标准的单位根检验方法可能会产生有偏差的估计量。尽管我国目前的通货膨胀率基本上是处于一种相对较低且稳定的状态，但是由于经历过几次剧烈的通货膨胀过程，因此通货膨胀率可能存在着一些异常值。从而运用传统方法来分析就会存在一定的偏差，而分位数自回归方法则可在存在异常值或非正态分布相关设定误差的情况下，给出一种稳健的估计量（Koenker&Xiao，2004）[2]。同时，分位数自回归方法允许通货膨胀在其不同的分位数区间具有不同的或是非对称的调整速度，这说明通货膨胀向其长期均衡状态调整的速度可能由于受到冲击大小而不同。本文中所要检验的就是通货膨胀受到冲击时向其均衡状态动态变化的行为是否存在这种非对称性。因此，本文参考（Cicek&Akar,2013）[3]运用分位数自回归方法来研究我国通货膨胀的动态行为，这对于国家准确地把握宏观经济形势从而制定合适的宏观调控政策具有重要的参考意义。

一、国内外文献综述

国外学术界对于通货膨胀的动态行为进行了大量实证研究，早期的研究中重点考察的是运用单变量单位根检验来判断通货膨胀率是否是一个单位根过程，其中一些研究并未考虑通货膨胀的持久性程度，并且未能提供支持通货膨胀向均衡状态调整的经验数据（Ng&Perron,2001;O’Railly&Whelan,2005;Ho,2009等）[4][5][6]；其他一些研究则认为通货膨胀是平稳的（Bailie et al.,1996; Rose,1998）[7][8]。Levin&Piger(2004)研究认为，由于货币政策框架的变化而未考虑结构断点的通货膨胀持续性模型，可能会导致存在一个单位根，而这个检验结果是有偏误的[9]。学者们通过Chow检验方法来考虑结构断点已经为发现通货膨胀向其均衡水平调整提供了强有力的支持，其中Cechette&Debelle（2006）运用该方法考虑结构断点的Quandt-Andrews检验，研究结果表明，通货膨胀受到冲击时向其均衡水平的调整是不持久的[10]。除此之外，Taylor（2000）和Ball&Sheridan（2003）也得到了同样的结果[11][12]。相反，O’Reilly&Whelan(2005)和Pivetta&Reis（2007）运用滚动窗口估计法研究发现，通货膨胀接近于一个单位根过程，并且通货膨胀持续性的减少也是不明显的[5][13]。从其他国家来看，对于通货膨胀是否具有持续性也尚未达成一致意见。Alper&Ucer（1998）运用VAR模型研究认为通货膨胀具有持续性[14]。Tutar（2001）运用ECM模型研究表明，以PPI计算的通货膨胀率是一个单位根过程[15]。Baum et al.（1999）研究发现，以CPI和PPI计算的通货膨胀率均是单位根过程[16]。而Erlat（2001）运用分整自回归移动平均（ARFIMA）模型检验通货膨胀持续性的动态性，研究表明，CPI和PPI均是平稳的，但是一般存在显著的长记忆部分[17]。上述研究重点在于考虑通货膨胀率的平均行为，未能捕捉冲击的大小及符号对通货膨胀的影响效应，或者说未表明通货膨胀是否存在非对称的均值回归过程。基于此，Cicek&Akar（2013）[3]运用分位数自回归方法检验了通货膨胀均值回归问题，这个方法同时允许我们去量化各种冲击对通货膨胀的影响，并且可以捕捉通货膨胀向其稳定状态调整可能存在的非对称性。

国内近年来对通货膨胀调整的动态性方面的研究较少，对通货膨胀调整的非对称性方面也只是略有涉及。其中，赵留彦等（2005）使用两区制马尔柯夫转移模型，研究了我国高水平通胀与低水平通胀的非线性转移特征[18]。王少平等（2006）使用两区制的STAR模型研究了我国1952-2004年的通货膨胀率，研究结果表明，我国通胀率具有明显的非线性调整机制，通货膨胀与通货紧缩相互转移的临界水平为3.3%[19]。张屹山等（2008）使用门限自回归模型的研究结果表明，我国通胀率变化可以划分为加速通胀与减速通胀两种状态，并且两种状态具有很高的持续性[20]。另外，张凌翔等（2011）[21]运用多区制平滑转移自回归模型（STAR）来划分通货膨胀的周期，并采用集中非线性单位根检验方法检验通货膨胀率的平稳属性，归纳了通货膨胀在各区制中相互转移的典型路径，最后使用广义脉冲响应方法分析了通胀率各区制非线性的动态调整特性及政策含义。该文研究得出，冲击对通胀系统不具有持久性影响，但正向冲击与负向冲击的影响则具有非对称性。目前，最新的研究中陈雄强、张晓峒等（2013）运用分位数自回归模型考察通货膨胀的持久性问题并探讨了通货膨胀调整的非对称性，研究得出中国的通货膨胀率具有高持久性，从低分位区间到高分位区间持久性逐渐增强。该文章也得出了通货膨胀率的动态调整具有非对称性的特征，并且得出该模型可以有效区分均衡点和非均衡点，从而为央行构建预警机制，监测和调控通货膨胀提供依据[22]。

综上所述，国内外学者关于通货膨胀动态行为方面的研究主要集中在通货膨胀的平稳性和持续性方面，并且相关研究尚未达成一致意见，而关于通货膨胀变化的非对称性或者说通货膨胀的均值回归过程方面的研究则较少。与国外研究不同，国内学者研究通货膨胀调整的非对称性问题主要选择的是马尔柯夫转移模型方法，这一方法的主要问题在于仅能给出各区制之间相互转移的概率，并不能明确给出不同的区制里通货膨胀受到不同冲击的反应情况。同时，最新的研究中，如陈雄强、张晓峒等（2013）虽然使用的是分位数自回归模型来判断通胀动态行为的持久性和非对称性，但并未考虑结构断点问题。因此，本文将在该研究的基础上，参考Cicek&Akar（2013）的研究，运用分位数自回归方法，考虑结构断点，从非对称性视角来检验我国通货膨胀率的动态行为。

二、计量经济方法介绍

如上文所述，本文运用分位数自回归方法（Quantile Autoregression Method）来捕捉不同冲击大小及符号下通货膨胀的调整速度。下面具体介绍这一方法。首先，考虑一个简单的高阶自回归模型作为ADF模型形式如下：

由上式可以看出，可以将yt的条件分位表示成一个线性函数。令，定义然后可以得到如下形式：

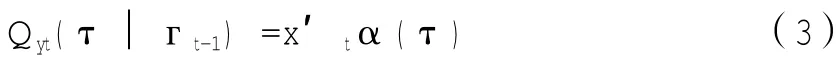
式（3）中的参数向量α(τ)可通过最小化下式得到：

本文中τi∈ψ，我们选择ψ=（0.1，0.2…，0.9）。上述tn(τ)统计量可以用来检验序列在每一个分位的持续性行为。另外，为了观察调整的速度，我们计算在每个分位区间里通货膨胀受到冲击的半衰期（Half Lives，简称HLs）。HLs值越高，说明调整的时期越长，其计算公式为HLs=log(0.5)/log (α1(τ))，其中α1(τ)为自回归系数。

本文中基于分位数方法的单位根检验需要检验所有分位区间的单位根性质。与此相关的用来检验原假设为各区间是常数单位根过程的是基于τ∈ψ的分位数自回归过程的Kolmogorov-Smimov（简称“KS”）统计量。Koenker&Xiao(2004)提出Quantile Kolmogorov-Smimov（QKS）检验统计量如下所示：

上式中，tn表示公式（5）中所定义的t-ratio统计量，tn(τ)由τ∈ψ计算，因此取其中最大值来构建QKS统计量。

三、实证分析结果

（一）数据和样本统计量

本文基于月度CPI数据来计算通货膨胀率指标，如图1所示，时间跨度为1990年1月至2013年5月，样本量为279，相关数据来源于国家统计局网站（http://www.stats.gov.cn/）。

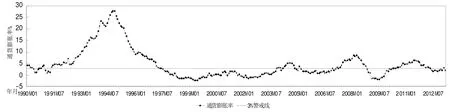
图1 中国通货膨胀率趋势图（1990-2013）

由图1可以看出，20世纪90年代以来我国通货膨胀率呈现了一种剧烈的波动趋势，基本上可以划分为高通货膨胀、通货紧缩和低通货膨胀三个时期，因此本文计算了不同时期中月度通货膨胀率的均值、中位数、标准误差、偏度、峰度以及Jarque-Bera（JB）正态性检验等统计量，结果如表1所示。

表1 样本统计量

表1中，偏度和峰度表明通货膨胀率可能并不服从于正态分布。一般情况下，峰度测量值高于3才与正态分布相关，上述结果说明分布为厚尾。JB检验表明在1%的显著性水平下拒绝正态分布假设。由于这种分布厚尾的特点，因此本文运用分位数自回归方法来进行实证研究是非常适合的。

（二）实证检验结果

本文基于通货膨胀率构建分位数自回归模型，我们事先假定通货膨胀的稳态水平为3%，运用STATA软件进行分位数单位根检验，得到各分位数τ=[0.1,…，0.9]的常数项[α0(τ)]和AR系数[α1(τ)]的估计值，以及具有一致性的HLs和QKS检验结果。其中，常数项[α0(τ)]的估计值可捕捉不同分位区间内通货膨胀冲击的大小，为负数表明负向冲击可能是由于紧缩性货币政策或经济衰退导致的（Tsong&Lee，2011）。AR系数[α1(τ)]的估计值可反映通货膨胀向其均值调整的速度。本文根据AR项系数的估计值计算HLs值，τ越大，AR系数越大，HLs值就越大，且HLs∈（0，∞），HLs值越大，表明调整所需的时间越长。例如在较高的分位区间里，α1(τ)系数接近于1或者略大于1，此时HLs值趋向于无穷，表明通货膨胀所受到的冲击是长期的，尤其是在较大的分位区间里。相反，通货膨胀在相对较小的分位区间里则是向均值调整的。换句话说，τ的最大分位数反映最大的正向冲击；最小的分位数反映最大的负向冲击。α1(τ)系数是随着分位区间的上升而增加的，通货膨胀所受冲击的符号对其向均值调整的速度来说是非常重要的。

表2 全样本模型估计结果

如表2所示，AR项[α1(τ)]的估计值提供了关于通货膨胀调整的重要细节。在不同分位区间里，通货膨胀调整过程具有非对称性。例如，在较小的分位区间里，通胀率受到负向冲击时就可以向其均值调整。同理，在较大的分位区间里，则不可行。由于正向冲击会降低向其均值调整的能力，同时HLs是无限大的，通货膨胀率表现为单位根行为。由表2所示，反映通货膨胀冲击的常数项值在至少60%分位区间以上均是大于0的，而通货膨胀的调整系数同样呈现一种正向趋势，其调整过程在较低分位区间里是加速的，在较高分位区间里是减速的，而且一直具有非对称性。

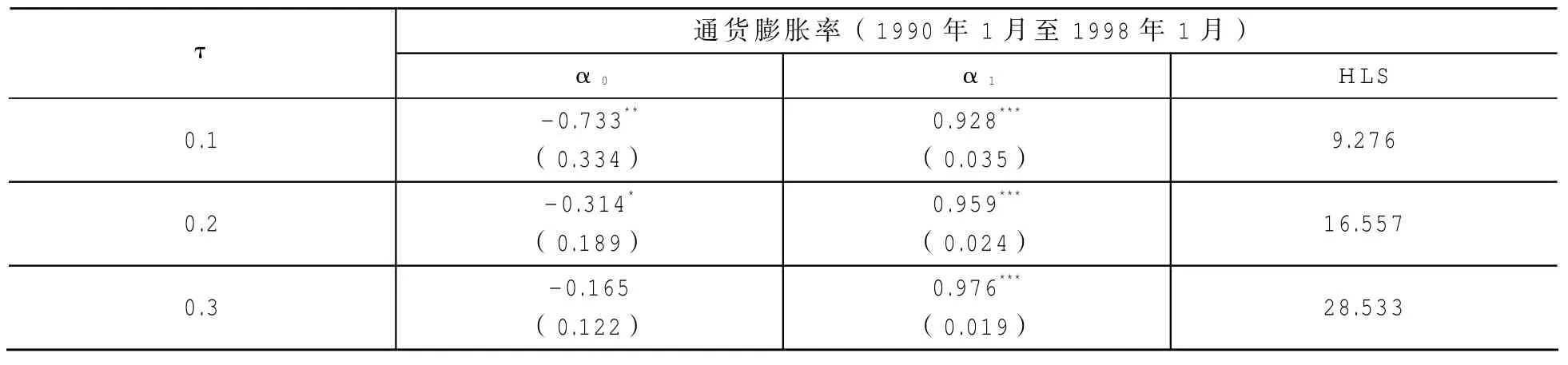
表3 高通胀时期模型估计结果

近年来，我国的货币政策调整较为频繁，可能存在若干个结构断点。本文运用Chow检验方法确定结构断点可知，我国通货膨胀率可能存在两个断点。我们将1998年和2002年作为结构断点，重新估计模型结果如表3、表4、表5所示。考虑结构变化，Oquz（2010）认为通货膨胀持续性是下降的。通胀预期也许是通胀持续性非对称性的最初原因，在高通胀预期情况下，工人期望更高的名义工资从而维持以前的财富水平，这可能会导致公司提高商品价格从而导致总体价格水平的提高。然而，在轻微通胀预期情况下，工人和公司也许不会去寻求更高的工资和价格，这就会导致通货膨胀有一个稳定的调整过程。由表3、表4、表5所示，除了在高通货膨胀时期的60%分位区间和低通货膨胀时期的80%分位区间外，在结构断点前后，虽然通胀的动态行为仍具有非对称性，但是持续值

是随着分位区间的上升而下降的。因此，在较高的分位区间里，通胀受到正向冲击以后便向其稳定水平调整。尽管从表2来看，通货膨胀率表现出了单位根行为，但是在不同的通货膨胀时期里，模型估计结果拒绝存在单位根的假设，即表明通货膨胀是一种平稳过程。

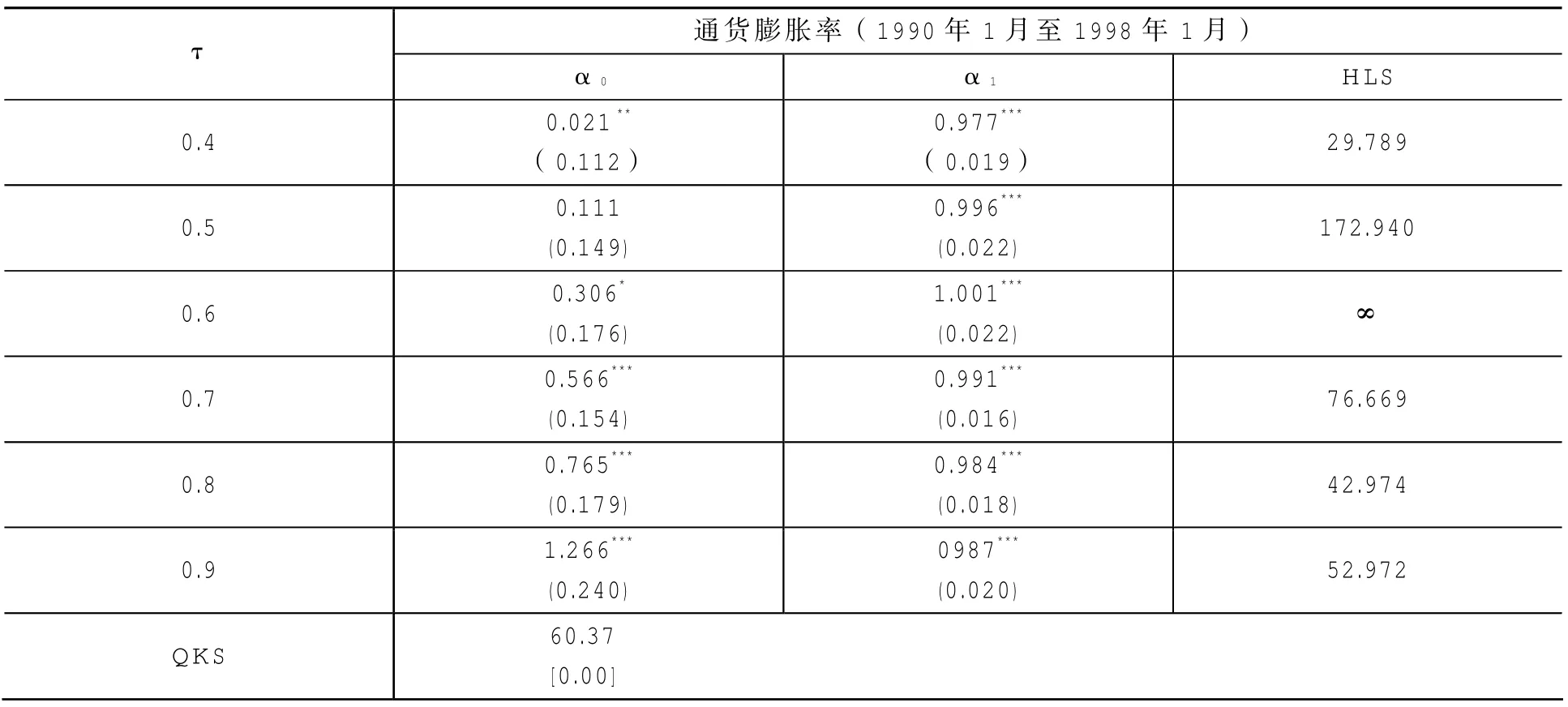
续表3

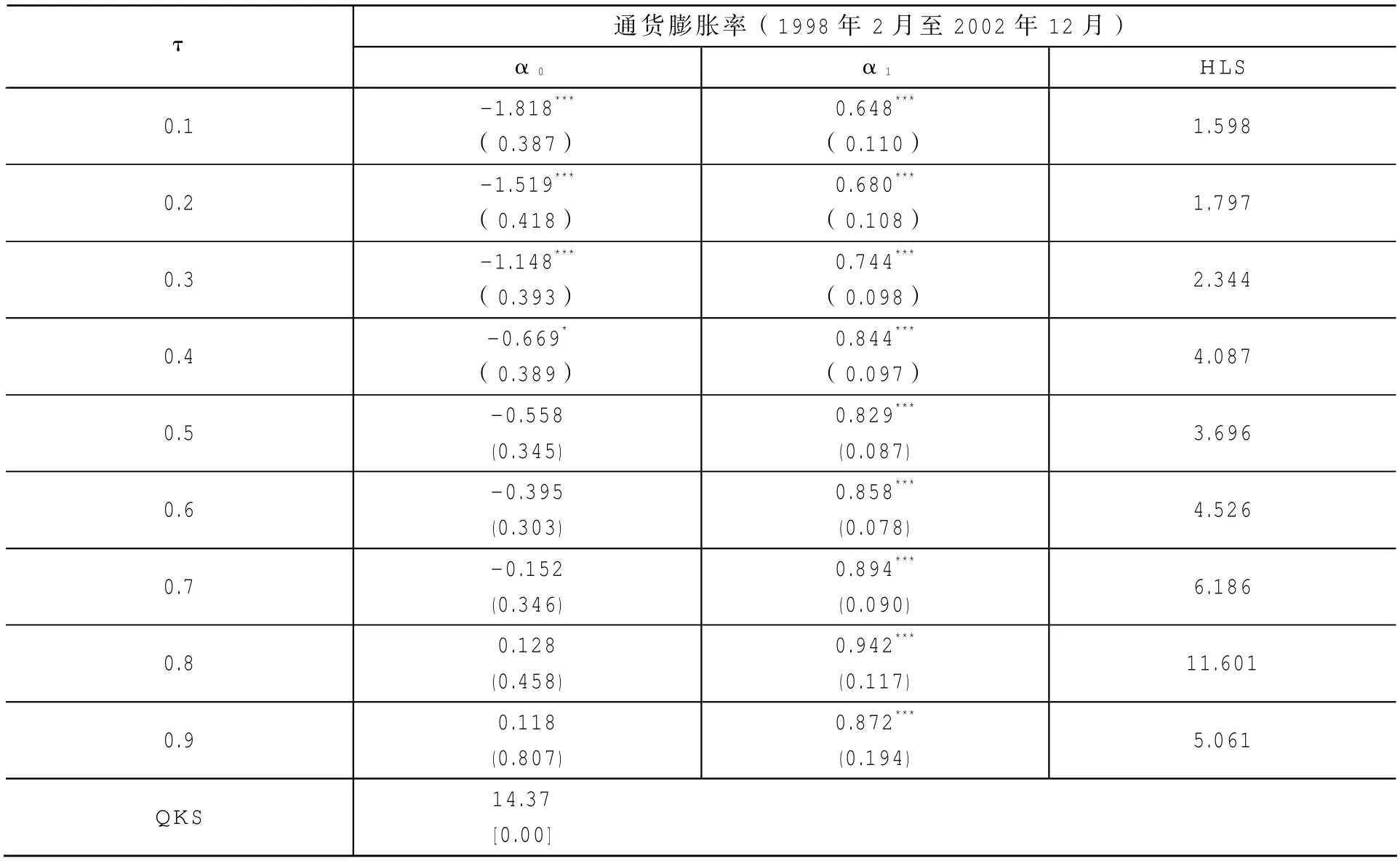
表4 通货紧缩时期模型估计结果

上述不同通货膨胀时期的模型估计结果表明，从整体来看，在较小的分位区间里，通货膨胀受到一个负向冲击以后，便可调整到一个稳定水平，而在较高分位区间里，受到一个正向冲击以后便表现为一个单位根行为，这说明通货膨胀的动态调整行为具有非对称性（这与现有文献研究结果相一致）。然而，考虑结构断点重新估计模型可知，在高通货膨胀时期与通货紧缩时期的结构断点前后，持续系数值有所降低，而在通货紧缩时期与低通货膨胀时期的结构断点前后，持续系数值则有所上升。持续系数值的下降表明在高通货膨胀时期，当经济受到过热冲击时，政府可以将通货膨胀相对较快地调整至长期均衡水平。而持续系数值的上升则表明在通货紧缩时期，当经济受到衰退冲击时，政府很难将通货膨胀相对较快地调整至长期均衡水平。但是除极个别分位区间的通货膨胀服从单位根过程外，在其他分位区间里通货膨胀不管受到正向还是负向的冲击，其向均值的调整均是一个平稳过程，但通货膨胀向其均值的调整过程仍具有非对称性。

表5 低通胀时期模型估计结果

四、结论

本文运用分位数自回归方法来研究通货膨胀率的动态行为，该方法可以不用事先假定时间序列的分布状况，并且允许在分布的不同分位区间存在不同的或非对称的调整速度。这种不同的或非对称性的存在表明通货膨胀向其长期均衡状态调整速度可能因所受冲击的大小及符号而不同。本文的实证研究结果验证了这种非对称性，从而可以为国家制定政策提供参考。因此，考虑我国通货膨胀动态调整行为的这种非对称性，在经济出现过热的时期，国家应出台较为缓和的紧缩性宏观调控政策，以免造成经济过快地下降，而在经济出现衰退的时期，国家应出台较为扩张性的宏观调控政策，从而促进整体经济恢复正常水平。

[1]Ozcan,K.M .,Berument,H .,Neyapti,B.,2004.Dynamics of infl-ation and inflation inertia in Turkey.Journal of Economic Cooperation25(3):63-86.

[2]Koenker,R.,Xiao,Z.,2004.Unit root quantile autoregression inference.Journal of the American Statistical Association99 (467),775-787.

[3]Serkan iek,Cüneyt Akar.,2013.The asymmetry of inflation adjustment in Turkey.Economic Modeling 31(3),104-118.

[4]Ng,S.,Perron,P.,2001.Lag length selection and the constru-ction of unit root tests with good size and power.Econo-metrica 69,1519-1554.

[5]O’Reilly,G.,W helan,K.,2005.Has Euro area in flation per-sistence change over time The Review of Economics and Statistics 87,709-720.

[6]Ho,T.W .,2009.The inflation rates may accelerate after all:panel evidence from 19 OECD economies.Empirical Eco-nomics 36,55-64.

[7]Baillie,R.T.,Chung,C.F.,Tieslau,M .A.,1996.Analysing infla-tion by the fractionally integrated ARFIMA-GARCH model. Journal of Applied Econometrics 11,23-40.

[8]Rose,A.K.,1998.Is the real interest rate stable Journal of Finance 43,1095-1112.

[9]Levin,A.Piger,J.,2004.Is inflation persistence intrinsic in industrial economies.ECB W orking Papers,No: 334.

[10]Cechette,S.G.,Debelle,G.,2006.Has the inflation process ch-anged Economic Policy46,311–352.

[11]Taylor,J.B.,2000.Low in flation pass-through and pricing power of firms.European Economic Review 44,1389-1408.

[12]Ball,L.,Sheridan,N.,2003.Does inflation targeting matter IMF W orking Paper,No: 129.

[13]Pivetta,F.,Reis,R.,2007.The persistence of inflation in the United States.Journal of Economic Dynamics and Control 31,1326-1358.

[14]Alper,C.E.,Ucer,M .,1998.Some observations on Turkish in-flation:a ‘random walk’down the past decade.Bogazici Jour-nal: Review of Social,Economic and Administrative Studies 12(1),7-38.

[15]Tutar,I.,2001.Inertial inflation and exchange rate based an-choring,Unpublished PhD Thesis,The Middle East Technical University,Ankara.

[16]Baum,R.T.,Barkoulas,J.T.,Caglayan,M .,1999.Persistence in in-ternationalinflation rates.Southern Economic Journal65,900-913.

[17]Erlat,H .,2001.Long memory in Turkish inflation rates.http://www.lu c.edu/orgs/meea/volume3/herlat/.

[18]赵留彦,王一鸣,蔡婧.中国通胀水平与通胀不确定性：马尔柯夫域变分析[J].经济研究,2005，(8):60-72.

[19]王少平,彭方平.我国通货膨胀和通货紧缩的非线性转换[J].经济研究,2006，(8):35-44.

[20]张屹山,张代强.我国通货膨胀率波动路径的非线性状态转换——基于通货膨胀持久性视角的实证检验[J].管理世界,2008，(12):43-50.

[21]张凌翔,张晓峒.通货膨胀率周期波动于非线性动态调整[J].经济研究,2011，(5):17-31.

[22]陈雄强，张晓峒，张庆昌.通货膨胀持久性及其非对称性研究——基于分位数自回归模型[J].经济与管理研究，2013，（3）：10-18.

（责任编辑：吴凌霄）

Dynamic Behavior Analysis of China’s Inflation in an Asymmetric Perspective

NIE Sa
(School of Economics,Yunnan Minzu University,Kunming 650031,Yunnan,China)

The quantile regression model is constructed to analyze the dynamic development trend of inflation rate in an asymmetric perspective based on monthly data from January 1990 to May 2013 in China.These results show that inflation rate can revert to the stable level after a negative impact in the lower quantile interval,while the inflation rate is a unit root process after a positive impact in the higher quantile interval. These show that inflation rate's dynamic adjustment behavior is asymmetric.Then,according to the structural breakpoints,the reestimate model shows that the inflation rate's dynamic adjustment behavior is a stationary process in most ways,while the inflation rate's adjustment is still asymmetric in different periods. Those empirical test results can be introduced to provide a realistic basis for the nation to manage inflation, promote the stable prices of macro-control policies.

inflation；asymmetric perspective；dynamic behavior；quantile auto regression model

F822.5

A

1671-0304（2014）06-0064-08

10.13880/j.cnki.cn65-1210/c.2014.06.009

2014-08-28

时间］2014-11-21 15:55

聂飒（1982-），女，辽宁铁岭人，云南民族大学经济学院讲师，博士，主要从事宏观经济分析与预测方面的研究。