基于MCI患者脑功能网络的分类研究

梁 红，相 洁

（太原理工大学计算机科学与技术学院，山西太原030024）

0 引 言

阿尔茨海默病（Alzheimer’s disease，AD）是一种神经退行性疾病，发病率高，病因和发病机制尚不明确，目前还没有有效的治疗方法。轻度认知障碍（mild cognitive impairment，MCI）是AD的前期阶段，每年以10%－l5%的高转化率发展为AD，而正常老年人每年的转化率仅为1%－2%。因此，对MCI的早期诊断或预测对延迟疾病进展至关重要［1，2］。然而，相比于AD患者，MCI患者的认知损伤程度较轻微，并没有明显的认知下降症状，采用目前的神经心理学测验和影像学检查等临床诊断方法难以确诊。如何识别出能用于早期发现的诊断标志物，尽可能地延迟MCI到AD的转化是目前的一个重要问题。

随着磁共振技术的发展，机器学习的方法已逐步应用于MCI功能磁共振（functional magnetic resonance imaging，f MRI）数据的研究中。已有研究表明，MCI与正常老年人的脑网络拓扑结构之间存在差异，全局属性表现为MCI的特征路径长度比正常人有所增加［3］，聚类系数也有所不同，局部属性表现为单个阈值下一些脑区的节点属性值显著高于或低于正常人［4］。一些学者将异常的聚类系数和功能连接值作为分类特征，运用支持向量机（support vector machine，SVM）算法，对MCI和正常人进行了分类研究［5，6］。

但目前MCI脑功能网络的研究都是对全局属性或者单一阈值下的局部属性进行的，尚没有在连续阈值空间下对MCI脑功能网络节点属性的相关研究。

本文分析了不同病程的MCI及正常人在连续阈值空间内脑功能网络节点属性的差异，将具有显著差异的节点属性作为分类特征，运用SVM分类算法进行了分类研究，以此来辅助MCI的诊断，为MCI的诊断提供新的视角。

1 支持向量机的基本原理

支持向量机是由Vapnik等提出的一种机器学习算法，以统计学和结构风险最小化为理论基础，不存在一般神经网络的局部极值问题，能很好的解决小样本、非线性和高维学习问题，在f MRI数据分析中表现出很大的优势，是当前比较主流的机器学习方法之一［7］。其基本思想是:将输入向量通过核函数映射到一个高维特征空间，然后在特征空间求最优分类面，即找到能把两类样本正确分开且分类间隔最大的分类面。

对于线性可分问题，设样本集为｛（xi，yi），xi∈Rm，yi∈｛1，－1｝，i＝1，2，…n｝，SVM的线性判别函数为g（x）＝（w·xi）＋b，对应的分类面为w·x＋b＝0。求最优分类面即找到满足条件

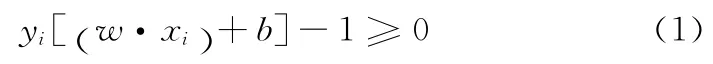
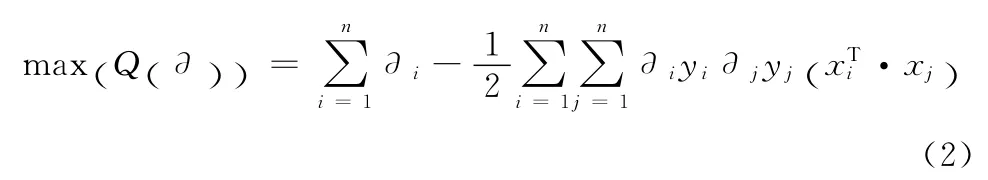
该函数为一个不等式约束下的二次函数寻优问题，有唯一解。求解上述问题后可得到最优分类函数

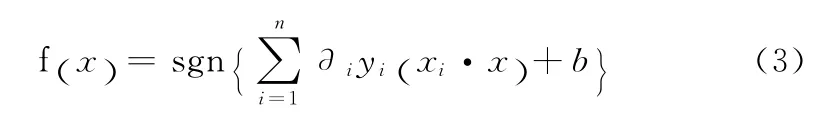
对于线性不可分问题，可以增加惩罚参数c（c为一个大于零的常数）和松弛变量ξi≥0，将约束条件（1）放松到

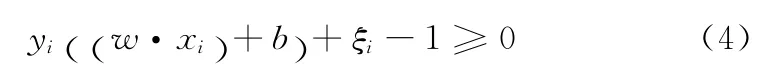
在条件（4）下求解下式

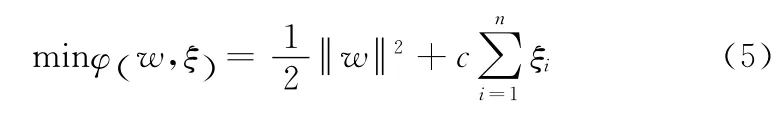
对于非线性问题，可通过非线性变换将输入空间变换到一个高维特征空间，继而在此空间中构造最优分类面。上述对偶问题只涉及样本间的内积运算（·xj），可以引入核函数K（x，y）替代上述的内积运算，因此，SVM的最优决策函数为

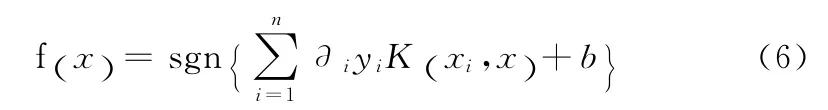
不同的核函数可以构造不同的支持向量机算法。目前比较常用的核函数有4类，包括线性核函数，径向基（ra－dial basis function，RBF）核函数，多项式核函数和S型核函数。

2 数据采集与预处理

2.1 被试

本实验的所有数据来源于ADNI（Alzheimer’s disease neuroimaging initiative）数据库。ADNI是由美国国立老年研究所（national institute on aging，NIA）于2003年创建的，旨在通过分析各种医学成像数据来研究老年痴呆疾病的发病机理及预防治疗手段。该数据库首次引入了早期轻度认知障碍（Early MCI，EMCI）和晚期轻度认知障碍（late MCI，LMCI）的概念，两者都是AD的早期阶段，区别在于逻辑记忆延迟回忆的损伤程度，目的是能在AD的更早期阶段就发现病情并给予有效的干预治疗。

参与实验的所有被试的年龄均介于55－90岁，有精神药物治疗的被试已排除在外。被试的入组标准描述如下:①正常对照（normal controls，NC）:简明精神量表（minimental state examination，MMSE）得分介于24－30，临床老年痴呆量表（clinical dementia rating，CDR）得分为0，非抑郁，非MCI，非痴呆；②EMCI:MMSE得分介于24－30，CDR为0.5，由韦氏记忆量表的延迟记忆部分测得客观的记忆丧失为（教育年限得分:（16年:9－11分；8－15年:5－9分；0－7年:3－6分），基本日常生活能力正常，无痴呆；③LMCI:除了韦氏记忆量表的延迟记忆部分测得的客观记忆丧失得分与EMCI不同（教育年限得分:（16年:（8分；8－15年:（4分；0－7年:（2分），其余标准同EMCI［8，9］。

本实验总共收集了70名被试，包括25名LMCI患者，16名EMCI患者和29名正常对照。被试的基本信息见表1。

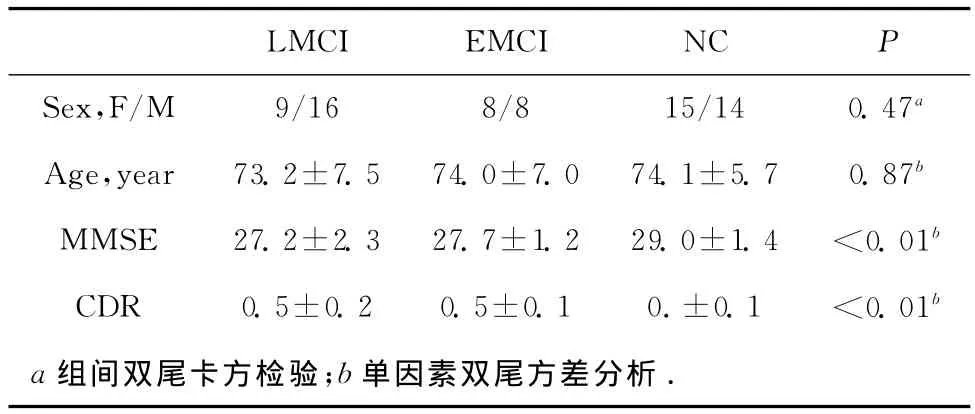
表1 被试基本信息

2.2 数据预处理

本实验的所有静息态f MRI数据及其对应的T1结构像数据均采用Philips 3.0T磁共振设备完成。整个扫描过程中，被试需睁眼保持清醒，放松，尽量不要动。为了便于预处理，下载的数据均为Analysis格式，具体采集过程及扫描参数详见ADNI网站（http://www.loni.ucla.edu/ADNI）。

对获得的原始数据采用DPARSF（data processing assis－tant for resting－state f MRI）［10］软件进行数据预处理。首先去除每个被试的前10个时间点，然后对剩余的130幅图像进行时间片校正和头动校正，去除水平头动大于3mm且转动大于3度的被试。接着对头动校正后的f MRI图像进行空间标准化，图像进行12维度的优化仿射变换，将其标准化到3mm体素的MNI标准空间中。之后对图像数据以4mm的全宽半高（full－width at half maxi－mum，FWHM）进行高斯平滑，以提高图像的信噪比。最后进行低频滤波（0.01－0.08Hz），以降低低频漂移及高频的生物噪音。

3 网络构建及特征提取

预处理完的f MRI图像，采用国际脑成像领域广泛使用的AAL（automated anatomical labeling）［11］模板，将大脑分割为90个（左右半脑各45个）感兴趣区（regions of interest，ROI），每个ROI定义为一个节点。一个ROI内所有体素的时间序列的均值定义为该节点的时间序列。计算任意两节点的平均时间序列之间的偏相关系数，得到90×90的关联矩阵。通常，根据设定的阈值，将关联矩阵转化为二值矩阵。即当相关系数大于该阈值时，二值矩阵的对应元素为1，否则为0。但如果对每个被试设置相同的阈值，被试网络中边的数量可能会不一致，这将导致脑功能网络的节点属性分析上存在差异。因此，本文采用稀疏度来确定阈值。稀疏度是指网络中实际存在的边数与可能存在的最大边数的比值。本实验选择一个较宽的连续的稀疏度范围8%～40%（间隔0.01），该范围内每个被试的网络都是连通的［12，13］。

完成网络的构建后，针对每个选定的稀疏度，计算每个被试的节点属性值，包括度、中间中心度及节点效率［14，15］。

节点i的度定义为与该节点相连的边的数目，其公式可表示为

式中:aij——网络中第i个节点与第j个节点之间的连接数。

节点i的中间中心度定义为网络中所有的其它节点对之间最短路径中通过该节点的最短路径数，其公式可表示为

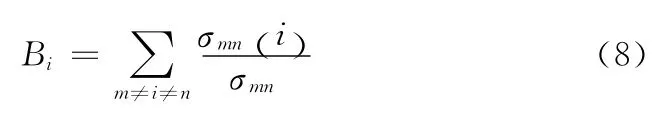
式中:σmn——节点m和n之间的最短路径数，σmn（i）——节点m到n经过的最短路径数，反映了节点i在网络中的重要性。

节点i的节点效率定义为该节点与网络中其它节点的最短路径倒数之和的平均值，其公式可表示为

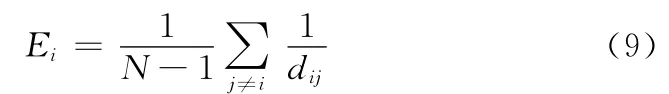
式中:dij——节点i和j之间的最短路径长度，反映了该节点到网络中其它节点的难易程度。这里的最短路径长度是指两个节点之间最短的那条路径的长度。

为表征这3个节点属性在所选的连续阈值空间内的整体特性，对每个节点特征计算其稀疏度空间下的曲线下面积（area under the curve，AUC），AUC是在特定的稀疏度空间内某个网络属性值的曲线下面积，其公式可表示为

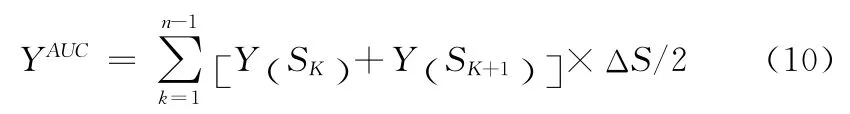
式中:S1、Sn——稀疏度的上下边界，ΔS——稀疏度间隔。本文中S1为0.08，Sn为0.40，ΔS为0.01。已有研究已证实该特征对脑网络拓扑属性的改变是非常敏感的［16，17］。

4 分 类

4.1 统计分析

采用非参数置换检验方法对任意两组被试的每个节点属性的AUC值进行统计分析。与参数检验方法相比，这种检验方法可以不用对AUC值的分布作任何的假设。各组间具有显著差异（p＜0.05）的脑区如图1所示。该图采用了Brain Net Viewer（http://www.nitrc.org/projects/bnv）软件绘制。表2为图1对应的脑区的英文名称和中文名称。具有显著组间差异的节点属性的AUC值作为这两组待分类样本的特征。

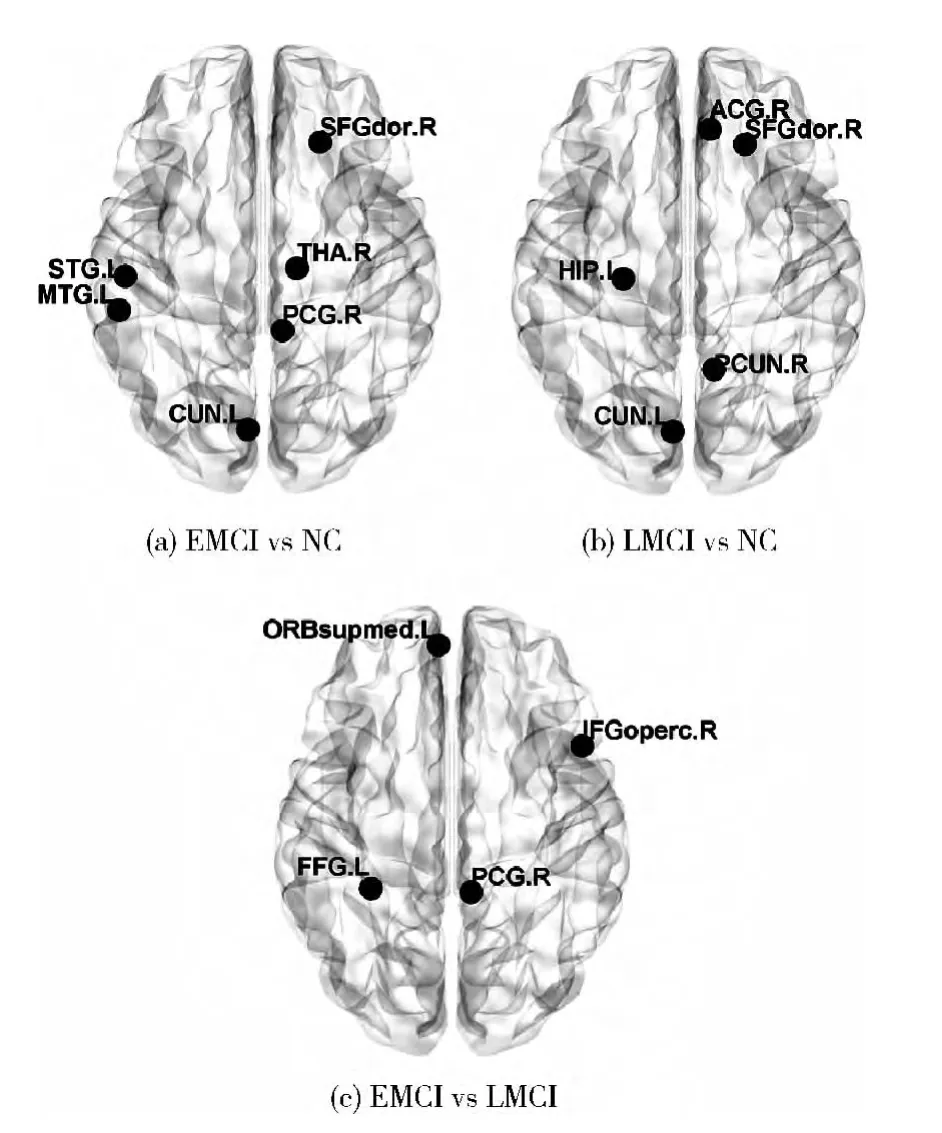
图1 组间差异脑区

4.2 分类过程及结果

本实验包括3个任务，分别为采用SVM算法对EMCI和NC，LMCI和NC及EMCI和LMCI进行分类判别，具体过程如下:

首先，从待分类样本中随机抽取2/3的被试作为训练集，剩余的1/3作为测试集。对训练集和测试集的特征数据进行归一化处理，取值范围为［－1，1］。

其次，选取RBF函数作为SVM算法的核函数。关于核函数参数的优化，国际上并没有公认统一的最好的方法，目前常用的是网格搜索和交叉验证相结合的方法，即让惩罚因子c和核函数参数g在一定范围内取值，对于每一组取定的c和g，在训练集上采用交叉验证的方法得到在此组c和g下训练集的分类正确率，最终选取使得训练集分类正确率最高的那组c和g作为最佳参数。本文中取c＝［2－10，2－9，…，29，210］，g＝［2－10，2－9，…，29，210］，交叉验证取10－Fold交叉验证。

最后，在训练集上用得到的最佳参数c和g进行样本训练，得到SVM分类模型，之后将测试样本输入到SVM分类模型中进行判别。实验结果见表3。

表2 脑区名称

表3 分类正确率

5 结束语

本文以复杂网络理论为基础，构建了EMCI，LMCI和NC三组被试在连续阈值空间下的静息态脑功能网络，利用统计学方法对该阈值范围内的节点属性的AUC值进行了差异分析，将具有显著组间差异的AUC值作为分类特征，运用SVM机器学习算法对任意两组被试进行了分类研究。实验结果表明，具有显著组间差异的脑区，包括扣带回，颞叶，额叶，顶叶的一些区域，与前人的研究结论一致［3，4］，这些异常的脑功能网络节点属性作为分类特征可以区分不同病程的MCI患者和正常被试，及不同病程的MCI患者。因此，该方法可以用于MCI的辅助诊断，以及时发现早期病情。

［1］Misra C，Fan Y，Davatzikos C.Baseline and longitudinal patterns of brain atrophy in MCI patients，and their use in prediction of short－term conversion to AD:Results from ADNI［J］.NeuroImage，2009，44（4）:1415－1422.

［2］Ron B，Elizabeth J，Kathryn Z G，et al.Forecasting the global burden of Alzheimer's disease［J］.Alzheimer's and Dementia，2007，3（3）:186－191.

［3］Wang J H，Zuo X N，Dai Z J，et al.Disrupted functional brain connectome in individuals at risk for Alzheimer's disease［J］.Biological Psychiatry，2013，73（5）:472－481.

［4］Liu Zhenyu，Zhang Yumei，Yan Hao，et al.Altered topological patterns of brain networks in mild cognitive impairment and Alzheimer＇s disease:A resting－state f MRI study［J］.Psychiatry Research:Neuroimaging，2012，202（2）:118－125.

［5］Li Y，Wang Y，Wu G，et al.Discriminant analysis of longitudinal cortical thickness changes in Alzheimer's diseaseusing dynamic and network features［J］.Neurobiology of Aging，2012，33（2）:427.e15－427.e30.

［6］Wee Chong－Yaw，Yap Pew－Thian，Zhang Daoqiang，et al.Identification of MCI individuals using structural and functional connectivity networks［J］.NeuroImage，2012，59（3）:2045－2056.

［7］Kohannim Omid，Hua Xue，Hibar Derrek P，et al.Boosting power for clinical trials using classifiers based on multiple biomarkers［J］.Neurobiology of Aging，2010，31（8）:1429－1442.

［8］Aisen P S，Petersen R C，Donohue M C，et al.Clinical core of the Alzheimer's disease neuroimaging initiative:Progress and plans［J］.Alzheimer's Dementia，2010，6（3）:239－246.

［9］Michael W Weiner，Paul S Aisen，Clifford R Jack Jr，et al.The Alzheimer's disease neuroimaging initiative:Progress report and future plans［J］.Alzheimer's Dementia，2010，6（3）:202－211.

［10］Yan C G，Zang Y F.DPARSF:A MATLAB toolbox for“Pipeline”data analysis of resting－state f MRI［J］.Front Syst Neurosci，2010，4:13.

［11］XUE Shaowei，TANG Yiyuan，LI Jian，et al.Method for constructing brain functional networks based on f MRI data［J］.Application Research of Computers，2010，27（11）:4505－4507（in Chinese）.［薛绍伟，唐一源，李健，等.一种基于f MRI数据的脑功能网络构建方法［J］.计算机应用研究，2010，27（11）:4405－4407.］

［12］Yao Zhijun，Zhang Yuanchao，Lei Lin，et al.Abnormal cor－tical networks in mild cognitive impairment and Alzheimer's disease［J］.PLoS Computational Biology，2010，6（11）:e1001006.

［13］He Y，Chen Z，Evans A.Structural insights into aberrant topological patterns of large－scale cortical networks in Alzheimer's disease［J］.The Journal of Neuroscience，2008，28（18）:4756－4766.

［14］TIAN Lixia.Analysis of complex brain networks based on graph theory［J］.Beijing Biomedical Engineering，2010，29（1）:1－7（in Chinese）.［田丽霞.基于图论的复杂脑网络分析［J］.北京生物医学工程，2010，29（1）:1－7.］

［15］Sophie Achard，Ed Bullmore.Efficiency and cost of economical brain functional networks［J］.PLoS Computational Biology，2007，3（2）:e17.

［16］Zhang Junran，Wang Jinhui，Wu Qizhu，et al.Disrupted brain connectivity networks in drug－naive，first－episode major depressive disorder［J］.Biological Psychiatry，2011，70（4）:334－342.

［17］Wang Jinhui，Wang Liang，Zang Yufeng，et al.Parcellation－dependent small－world brain functional networks:A resting－state f MRI study［J］.Human Brain Mapping，2009，30（5）:1511－1523.