读懂学生困惑 巧妙提出问题
魏艳红
一节课是否有效,关键要看问题的设计是否有效,是否能够激发学生的兴趣,引起学生积极的思考,达到让学生掌握并理解知识的目的。而一个智慧的教师如果仅仅抓住课堂的主问题是远远不够的。主问题是课堂的好问题,那些在学生思维的拐角处、困惑处设计的小问题也可以是课堂的好问题。我们要能够机智地发现并抓住来自学生中的真问题,了解学生思维的生长点,挖掘埋藏于学生背后的知识,才能真正地发挥学生的潜力,才能彰显课堂的魅力,才能使课堂变得更加丰厚。
例如,在教学小数乘法,探究积与自己本身大小关系的规律时,课堂上就出现了意想不到的精彩场面:2.8×1.5○2.8。
师:猜一猜,你认为谁大?
生1:我认为2.8大,因为2.8乘的是一个小数,积就一定比它自己要小,所以2.8大。
生2:(立刻反驳)不对,2.8×1.5的积大。因为2.8×1就已经是2.8了,那么2.8×1.5就是2.8的1倍都多了,所以2.8×1.5的积大。
听着两位同学的观点,大家觉得说的都有道理,也弄不清楚到底是哪个观点是正确的。在这种争执不休的情况下,我顺水推舟:
师:那该怎么办?怎样才能比出它们的大小呢?
生3:(过了片刻)我们可以算一算。
受了生3的启发,学生立刻计算起来,不一会儿,得出了结论:2.8×1.5=4.2,4.2>2.8,证实生2的观点是正确的,但是学生并不理解生2的想法,不知道他要表达的意思是什么。此时,如果教师小结“一个数乘一个大于1的数,积一定比它自己要大”的规律而结束这个环节,势必会让学生机械地加以记忆,并不能够真正理解规律的内涵。为了挖掘这道题背后隐藏的价值,使学生更深入地理解这一规律,我没有急于总结,而是做了机智的处理,我把生2请到了讲台上。
师:有没有更好的方法能让大家听明白你的想法?
听了我的问话,生2若有所思地低头思考起来。这时,我心里想:如果生2交流时,大家仍不明白他的想法,我会做他的小助手,帮他在黑板上画图来理解。可是出乎我意料的是,经过短暂思考的生2竟然边说想法边画出了线段图:
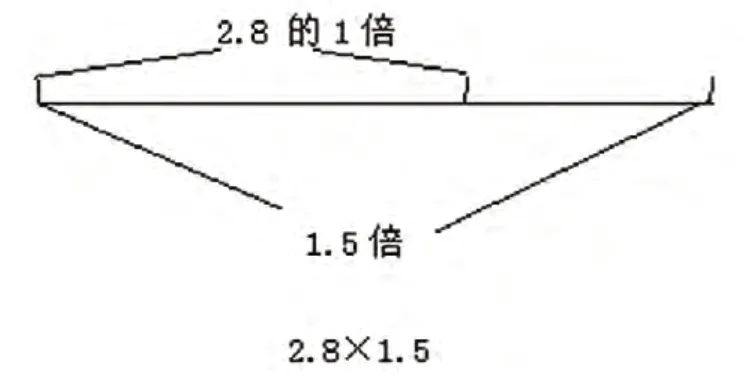
生2:用一条线段表示2.8,那么2.8的1.5倍就是2.8的1倍还多出半倍,也就是2.8的1倍半,肯定比2.8要大,而且大出了它的半倍,所以不用计算就可以知道2.8×1.5的积比2.8大。
听着生2的解释,看着他画的线段图,大家都豁然开朗了,不由得鼓起掌来。
我随后出示了第二题:2.8×1○2.8。借助线段图学生理解起来就很轻松了:2.8×1就是2.8的1倍,大小相等,不存在任何争议。而第三题2.8×0.7○2.8的出现,则把学生的思维又一次引向了深入:依据第一题和第二题的经验,学生不难判断2.8×0.7的积肯定比2.8小,但是如何能像前两题一样也用线段图清晰地表示出来呢?这是学生思维困惑的地方,也是把学生思维引向深入的转折点,我抓住这个契机,做了巧妙的点拨。
师:大家回想一下,0.7可以转变成我们以前学过的什么数?
生4:(激动地)可以变成分数,0.7就是7/10。
生5:(受生4启发)7/10就是把2.8平均分成10份,占其中的7份。
生6:我可以画出它的线段图了。
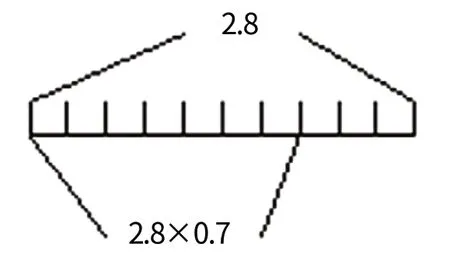
随着交流的深入,学生自然而然地便理解了“一个数如果乘一个大于1的数,则积比它自己大;如果乘一个等于1的数,则积和它自己相等;如果乘一个小于1的数,则积比它自己小”这一规律,应用起来也更加自如。我想,这样一个启发式的问题,不仅使学生理解掌握了规律,而且还沟通了分数与小数之间的联系,更重要的是架起了新旧知识之间的桥梁,为今后学习分数乘法应用题奠定了一个良好的基础,可谓是一举三得。

