三角形边的关系

设计：李建娜 点评：侯艳红

【教学背景分析】

1.教材分析。《三角形边的关系》是人教版实验教科书·数学四年级下册的一个章节，是在学生已经初步了解三角形基本概念基础上，进一步研究三角形的组成特征。教材重视体现知识的形成过程，而且留给学生充分进行自主探究的空间，让学生在动手操作、合作交流中发现并形成结论。

2.学情分析。学生已经知道三角形有三个边、角、顶点等知识，为研究边的关系做好了知识准备。学生生活中已积累了一些三角形三边关系的感性经验，但学生虽知道三角形有三条边，却不知道边的长短之间有怎样的关系。

3.我的思考。本节课教学活动主线是：什么样的三根小棒能围成三角形？围绕着这一主线引发学生探究的欲望，让学生通过猜一猜、摆一摆、想一想多种感官参与，重点研究能围成三角形的三条边之间到底有什么关系。

【前测题目】

1.填一填

（ ）的图形叫作三角形。

三角形有（ ）条边，（ ）个角。

调研目的：了解学生三角形的已有知识情况。

2.量一量

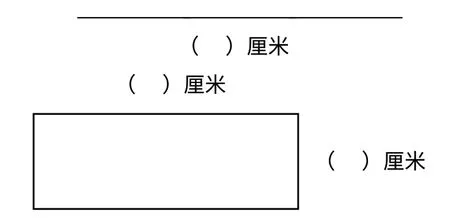
调研目的：了解学生对线段的测量方法是否准确。

3.想一想 鼠巢

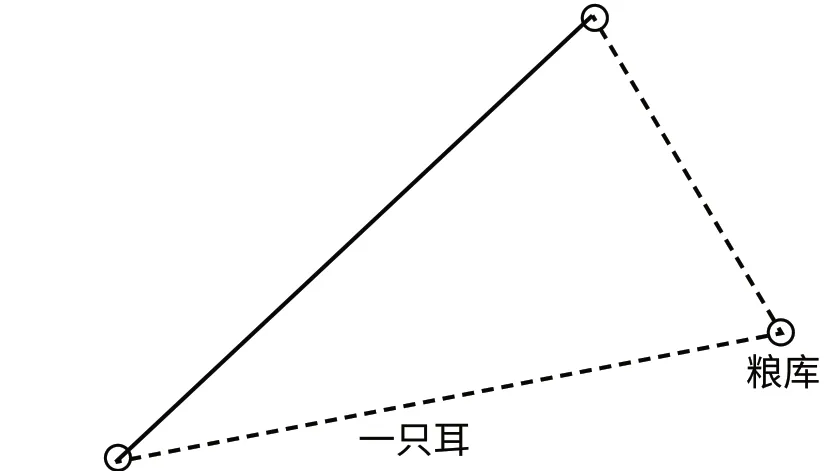
黑猫警长警局

一只耳逃离警局去粮库偷粮食，却被黑猫警长堵了个正着。虚线逃跑路线与实线抓捕路线谁近？

调研目的：了解学生实际生活中有关两边的和与第三边的比较方法。

4.我的再思考

三角形边的关系比较抽象，如何才能把知识的具体与抽象、静态与动态有机地呈现出来呢？关键是抓住“任意的三条线段能不能围成三角形？”引发学生探究的欲望，围绕这个问题让学生自己动手操作，发现有的能围成，有的不能围成，再由学生自己找出原因。

【教学目标】

1.通过猜、摆、算、想等活动，探究并发现“三角形任意两边的和大于第三边”的关系。

2.经历操作、发现、应用的过程，渗透数学思想与方法，培养自主探索、合作交流的能力。

3.激发学生探究的愿望和兴趣，培养参与数学活动的积极性和严谨的科学态度。

【教学重难点】

1.重点：探究并发现“三角形任意两边的和大于第三边”。

2.难点：理解“两条线段的和等于第三条线段时不能围成三角形”。

【教具准备】

课件，每小组5、8、10、12、20cm的小棒、实验报告单 。

【教学过程】

一、创设情境，激发兴趣

师：同学们，你们喜欢看动画片吗？羊村正在进行一场拼三角形比赛，谁先用这根小棒拼成三角形谁就获胜！

懒羊羊想也不想咔、咔剪成三段，“嗯？怎么围不成三角形呢？”

美羊羊先把小棒一分为二，再剪断其中一根，“咦？怎么也围不成？”

喜羊羊自信地说：“我知道一个有关三角形的奥秘，看我的！”他很轻松就围成了三角形！

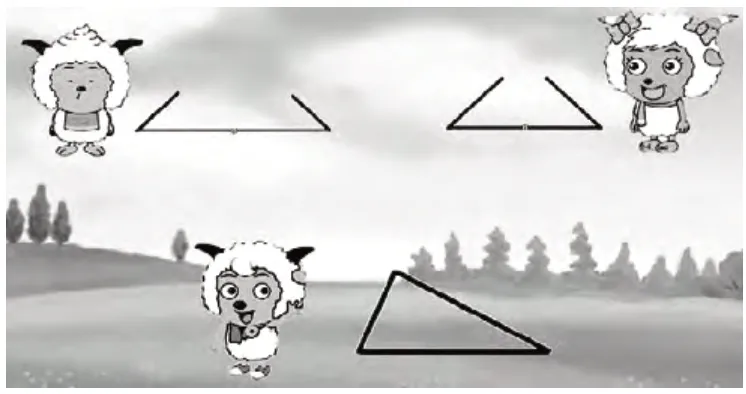
师：同样长的小棒，都是剪成了三截，为什么有的能围成三角形，有的却围不成？喜羊羊知道的有关三角形的奥秘是什么？看来能否围成三角形，与三条边的长短关系密不可分。今天我们就来研究：三角形边的关系。（由此揭示课题并板书：三角形边的关系。）

二、合作学习，探究新知

1.动手操作

师：三角形的三条边有什么关系呢？让我们通过摆三角形的实验亲自发现吧！我为每一小组准备了5根长度不同的小棒和一份实验记录单。

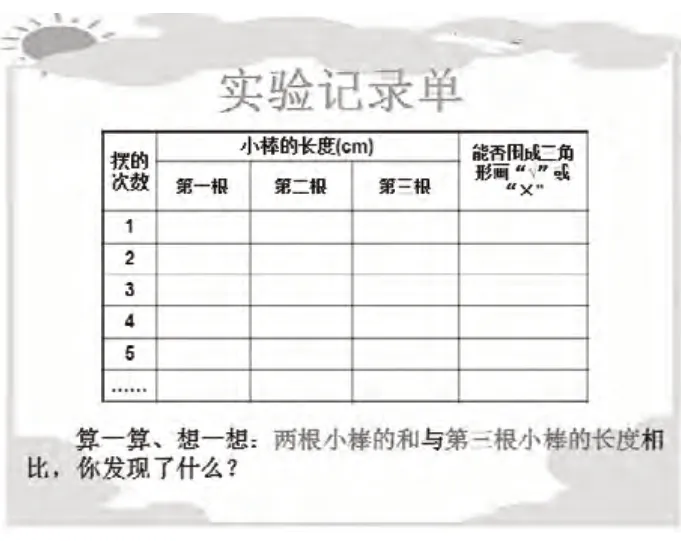
师：光有要求，从哪入手啊？实验要求会告诉你！来读一读吧！实验要求如下：

师：活动要求清楚了，接下来的时间交给你们自己动手发现吧！

学生在明晰活动要求后进行操作活动。

2.交流解惑

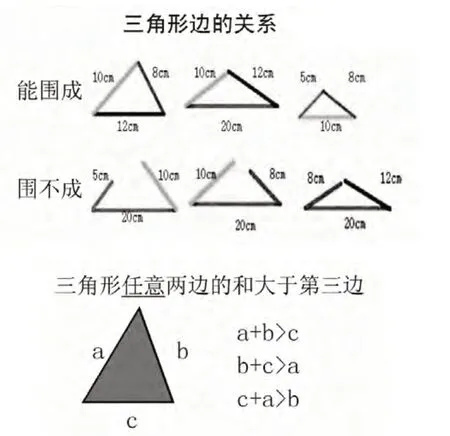
师：哪些小棒能围成三角形？哪些小棒围不成？（学生汇报，及时贴出图例。）

这组小棒20厘米、8厘米、12厘米引起学生的争议。

师：看来这组数据有争议，先把它放一边做个记号（？），一会儿再研究。

（1）观察这些能围成的三角形中三根小棒的长度有什么特点。

生1：两根小棒加起来比另一根长；

生2：我计算了 8+5>12，12+5>8，8+12>5。

追问：这个三角形的边有这样的关系，其他的呢？算一算吧！

小结：两边的和大于第三条边就能围成三角形。

构成过腔的不同音乐材料，无意间为过腔构筑起了多种不同的结构样式，使得过腔充满了无穷的活力，更重要的是，将过腔的结构与字腔本身固有的头、腹、尾腔的结构结合起来形成的字腔+（或 0）过腔①所谓“（或0）过腔”是说，不一定每个字腔都要带过腔，过腔的出现也根据艺术的需要。即使是0过腔，对每一个字腔来说，这个位置却是不可替代的。就像剧场中的座位，即使没人坐，但这个位置照样存在一样。这种结构，不仅是对传统曲牌音乐结构的重大突破，更是世所未见的、崭新的昆曲曲牌唱调的基本结构。

追问：只要有两边的和大于第三边就能围成三角形吗？

（2）引导学生观察围不成的情况。

这个△里也有两边的和大于第三边，可是还有5+8<20，所以围不成三角形。

对比明晰：必须是任意两边的和大于第三边才能围成三角形。

（3）到底两边的和等于第三边能不能围成三角形？

让持不同意见的学生到实物投影仪下，充分地展示交流。

由于小棒有一定的宽度，拼摆小棒的过程中总会有误差，说服力还不够。请孩子想象：当两根小棒的和与第三条边相等时，如果小棒变细一点，再细一点，会围成三角形吗？

课件演示突破难点：

演示一：这两条线段与第三条线段相接，向上一抬，就会出现缺口，不能首尾相连。

小结：两边的和等于第三边不能围成三角形。

（设计意图：本环节为学生提供足够的时间与空间，让学生亲自动手操作、观察、判别、表达、感受、理解三角形的三边关系。）

3.构建模型

师：在三角形中，能用字母表示三角形的三条边关系吗？

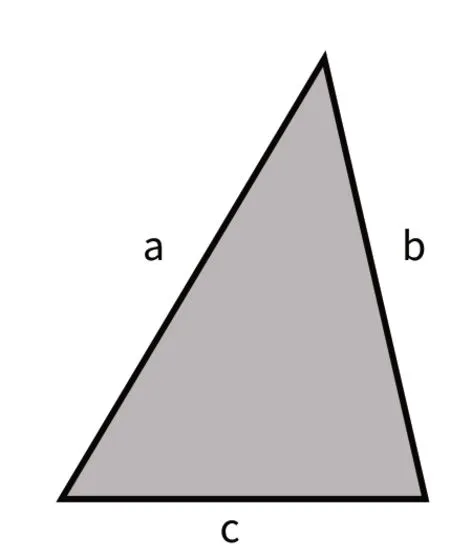
生：a+b>c，b+c>a，c+a>b。

（设计意图：在数学课程中，应当注重发展学生的符号意识和模型思想。通过字母表示使学生理解符号的使用是进行数学思考和数学表达的重要形式。）

三、联系生活，拓展应用

1.独立判断：这些小棒能拼成三角形吗？

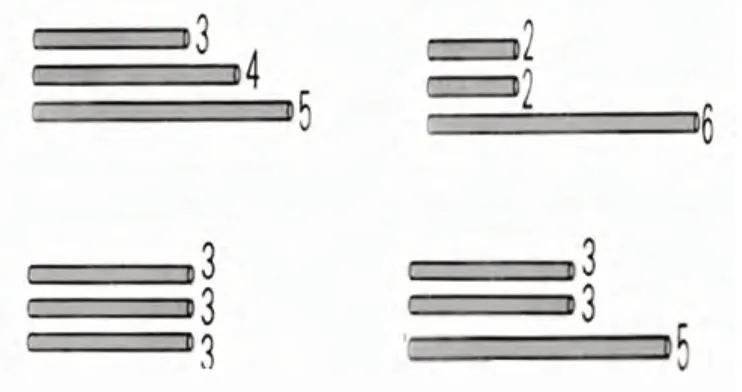
引导：最短的两条边3+4>5就能判断围不成三角形。

2.给小狗做一个三角形的房顶，两根木条分别是3分米、5分米，那么第三根可以是多少分米呢？（取整分米数）

3.过马路的学问：从A走到C，你建议大家怎么走？

为什么不直接从A走到C？为了人们安全便捷地出行，设计师设计了对角斑马线。

四、课外拓展，积淀文化

谁最早研究了三角形边的关系？欧几里得，最早对三角形边的关系做了深入研究，并给出完整证明的数学家！

（设计意图：引入课外知识，激发学生学习兴趣，使学生在获得知识的同时积淀数学文化。）

五、全课总结，完善新知

师：你在这堂课中有什么收获？

（设计意图：在课的结尾用这样的谈话的方式引导学生交流自己的收获和感受，将知识与情感融为一体。）

【板书设计】

【后测题目】

1.判断以下几组小棒能否围成三角形，能的打“√”

（1）3cm 4cm 5cm （ ）

（2）3cm 3cm 3cm （ ）

（3）2cm 2cm 6cm （ ）

（4）3cm 3cm 5cm （ ）

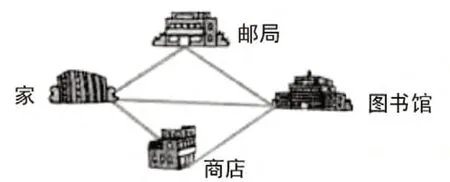
2.从家到学校哪条路最近？为什么？

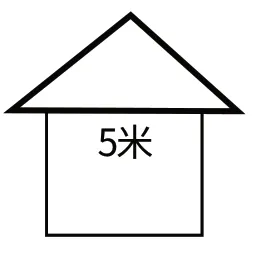
3.小小设计师

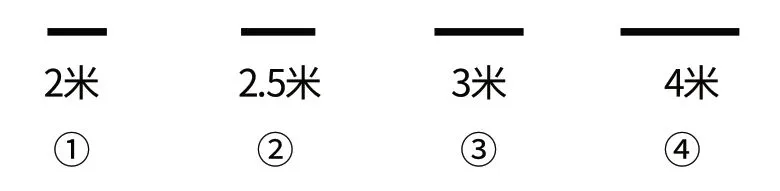
设计一个三角形屋顶，横梁长5米，下面的木料中，哪种长度的两根木料能与这根横梁组成三角形屋顶？

教学点评

预设是前提，生成是关键，将预设和生成结合起来不仅是一种教育的科学，更是一种教育的艺术。本节课很好地体现了“预设与生成”的有效结合，展现了“探索、发现”的全过程，使数学来源于生活、回归于生活，主要体现在：

一、有备而来，以预设为基础

在本节课中，李老师对教学内容、教学过程、教学方法等进行了充分的预设。

在引入环节设计的动画故事，一下吸引了孩子的注意力，拉近了距离；预设的问题：“同样的小棒，剪成了三段，为什么有的能围成三角形，有的却围不成？”激起学生的好奇心，从而激发学习欲望，为探究打下基础。在探究新知的过程中，李老师为学生提供了不同长度的小棒、实验要求和记录单等丰富的探究材料，并有目的、有意识地引导学生主动参与实践活动、经历知识的形成过程。对学生可能会遇到的问题和争议，做足了充分的预设，并制作动画，适时地给孩子们解惑。教师有备而来，顺势而导，这种预设越充分，生成就越有效。

二、即席创造，以生成为导向

生成是师生的“即席创造”，是“无法预约的美丽”。本节课李老师深入思考课堂教学的大方向、大环节，给学生提供了探究的时间，为生成腾出了时间和空间。李老师精当的点拨、讲解，对学生生成资源的适时运用，使课堂闪光，使学生顿悟，实现了学生在知识、方法的自我建构。

在学生产生争执时，李老师没有立刻作出明确的判断，而是肯定学生实事求是的态度和质疑的精神，解决了两边的和大于、小于第三边这两个问题之后，让持不同意见的学生到实物投影仪下展示交流，并从闭眼想象、课件演示两个角度突破此教学难点。

三、互动交流，以尊重为前提

新课标中指出：“学生是学习的主人，教师是学习的组织者、引导者和合作者。”本节课，在李老师的引导下学生积极参与，在探究新知的过程中互相提问、接纳、辩论、质疑，教师实时追问和点拨。师生互动、生生互动课堂上的主角不是教师而是学生，使课堂教学的有效性在无形中得到了提高。