季节性SARIMA模型在实验室开放管理中的应用
王法玉, 王静超
(天津理工大学 计算机实验教学示范中心; 智能计算及软件新技术重点实验室, 天津 300384)
0 引 言
高校实验室是高校从事实验教学、进行人才培养的重要场所[1]。为了进一步培养大学生的创新和实践能力,近年来,各高校纷纷建立了创新实验室,为学生提供课外第二课堂创新实践平台[2]。工程类实验教学不仅是教学的重要的组成部分,多样性的实验教学和开放性实验室也是教育改革的一项基本任务[3-5]。目前大多数学校都在实施实验室开放,对实验室管理也做了很多研究,并开发了一些实验室开放管理系统,但是多数管理系统都是只注重便捷,而对资源的利用率的研究比较少。
为了给学生提供一个开放自由的学习环境和足够的学习资源,培养学生的创新实践能力,我院自2000年以来实施了实验室开放政策,得到了广大学生的欢迎,学生的学习热情更加浓厚。但在实验室管理上,实验室上机人数的随机性和值班人员如何安排,却难以权衡,为了充分满足学生的需求,值班人员配备和开放实验室数量总是大于实际需求,造成值班人员安排和实验房间开放的数量难以确定,造成人力、物力和财力的浪费。为了更加有效利用和挖掘实验室资源,提高实验室和实验设备的利用率[6]。通过对几年来的实验室上机人数研究,发现实际的上机人数具有长期相关性, 也称自相似性, 即统计意义下的自相似性,具有成长性[7]。因此,本文利用时间序列分析法对实验室日常上机人数进行分析、研究和建模,进而对上机人数进行预测,旨在通过合理安排值班人员和开放实验室数量,达到节约资源的目的。
1 理论基础
时间序列分析是处理动态数据的一种比较有效的时域分析方法,通过观察动态数据的变化规律,对数据进行拟合,并对未来数据做出预测。在许多实际问题中,所观测到的数据序列{xt}常不是平稳序列,但如果将其做有限次差分处理后,可转化差分序列{Sn},是平稳序列,那么可用平稳信号序列模型来做研究[8]。
1.1 ARIMA模型
自回归移动平均(Auto-Regressive Integrated Moving Average,ARIMA)模型是由美国统计学家Box 和Jenkins 共同提出的,又叫B-J 模型[9]。该模型拟合的是差分平稳序列,实际上就是差分运算和ARMA 模型的结合。其基本建模思想和建模步骤可总结为:① 通过差分使非平稳过程变成平稳过程;② 建立描述该平稳过程的合适模型;③ 使用构建好的模型,预测将来值。ARIMA 模型是时间序列分析中重要的模型之一,目前广泛应用于各种领域[10-12]。
假设{xt/t=0,1,…}为非平稳随机序列,则ARIMA的一般形式为:

(1)
其中:
Φ(B)=1-φ1B-φ2B2-…-φpBp
Θ(B)=1-θ1B-θ2B2-…-φqBq

1.2 季节性SARIMA模型
季节性SARIMA 建模是在ARIMA 模型基础上发展起来的,用于具有周期性变化的序列的建模。在周期内,它提取当前时刻数据与前期数据的关联特征;在周期间,它提取当前时刻数据与前几个周期相同时刻的数据的关联特征[13]。将周期内特征和周期间特征结合起来,更加全面地描述序列的变化规律,得到的模型,对于序列变化情况的刻画也更加准确。因此,使用季节ARIMA 模型对季节性数据进行研究也是目前时序分析的热点[14-16]。

(2)
Θ(Bs)=1-Θ1Bs-Θ2B2s-…-ΘpBps
Φ(Bs)=1-Φ1Bs-Φ2B2s-…-ΦqBqs
式(2)的模型中季节差分仅仅消除了周期间相同周期点之间具有的相关部分,时间序列还可能存在长期趋势,一个周期内的不同周期点之间也具有一定的相关性,因此,由式(1)、(2)可得季节性ARIMA(p,d,q)(P,D,Q)s模型为:
1.3 ADF检验
ADF(Augmented Dickey-Fuller)检验是增项DF检验,ADF检验不仅可以检验AR(1)的平稳性,而且可以检验AR(P)过程的平稳性。
对于任意AR(P)过程,
Xt=φ1Xt-1+…+φpXt-p+εt
(3)
如果方程所有特征根都在单位圆内,则序列平稳;如果有一个特征根存在且为1,则序列为非平稳序列。
对式(3)进行变形简化后得:

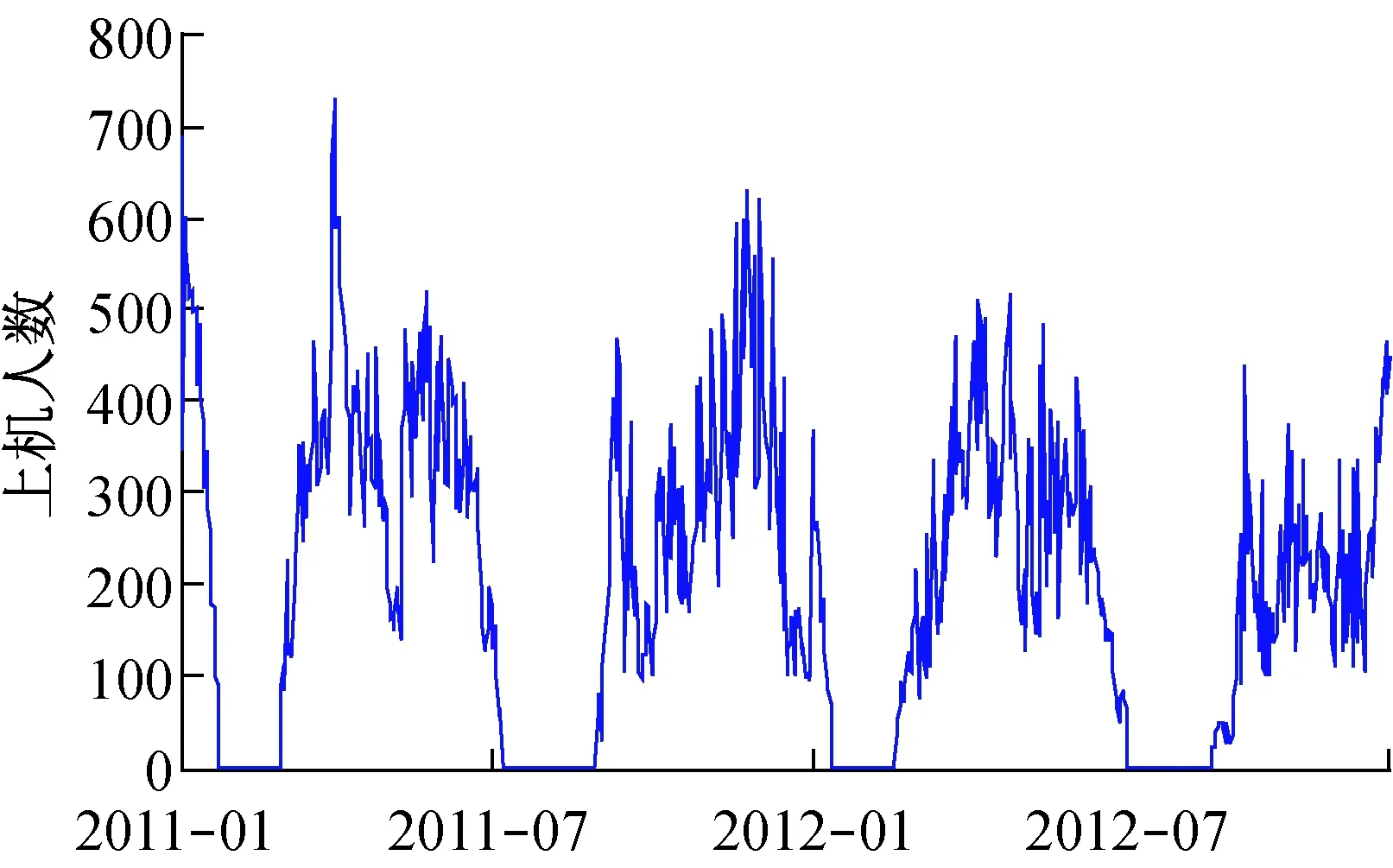
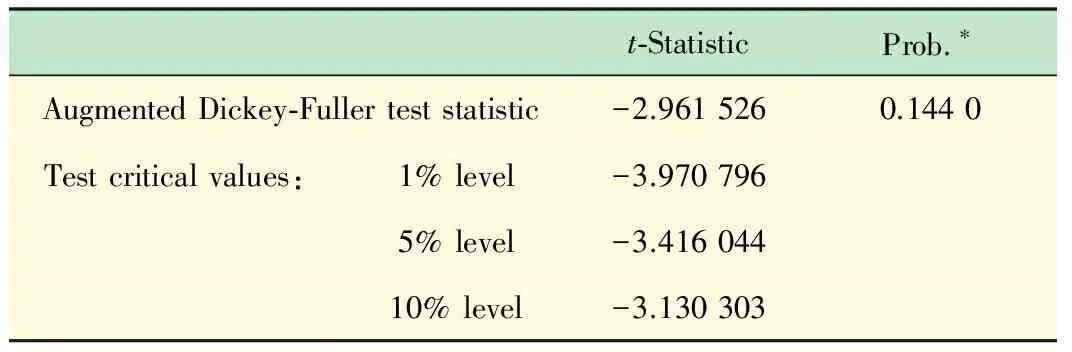
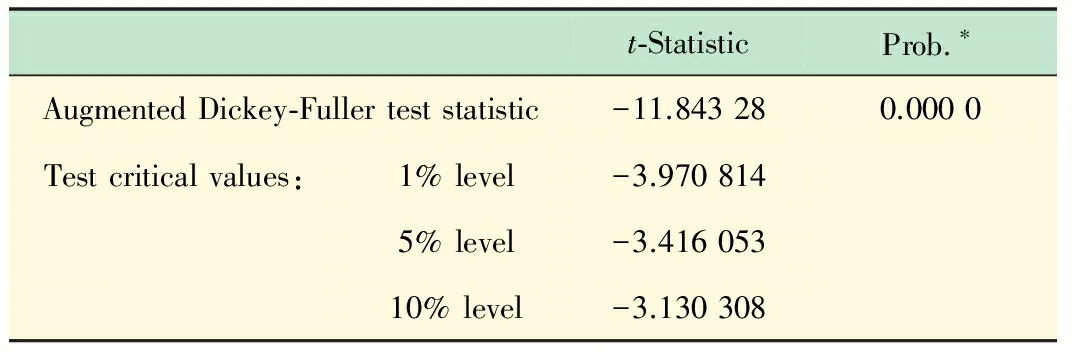
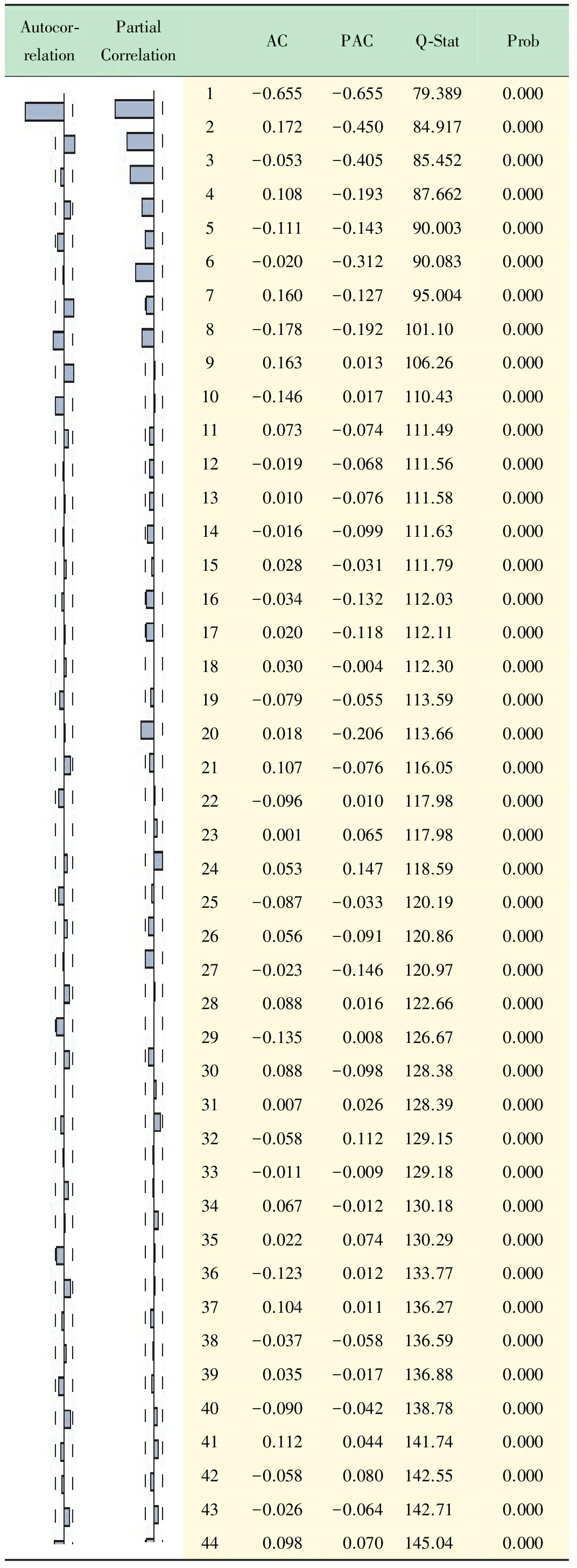
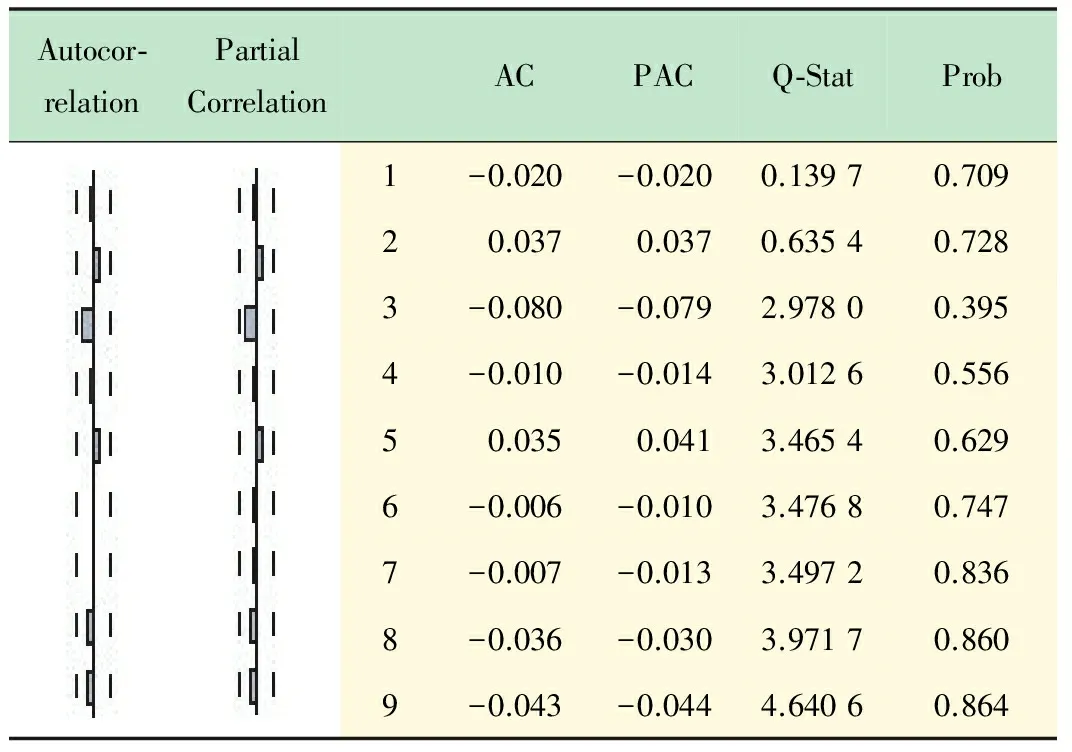
H0∶ρ=o↔H1∶ρ 构造ADF检验统计量: 通过Monte Carlo方法,可以得到ADF检验统计量的临界值表。 本文在季节性SARIMA模型构建过程中主要分为以下几步: (1) 平稳性检验。检验时间序列的平稳性,即确定d、D的大小,最直观的识别方法是自相关图法。如果自相关系数迅速趋于零,即自相关系数具有截尾性,则时间序列为平稳时间序列;如果时间序列存在一定的趋势性,则需要对原序列进行差分处理;如果时间序列存在异方差性,则需先对数据进行对数转换。 (2) 模型识别。模型识别即确定相应季节ARIMA模型的阶数p、q、P、Q的取值。一般情况下,可通过观察相关图估计模型阶数p、q、P、Q的可能取值,然后通过AIC、SC准则等,确定最合适的模型阶数,AIC值和SC值都是越小越好。 (3) 用最小二乘法进行模型估计。最小二乘法估计是线性模型中最常用的估计方法,具有良好的统计性质,且计算简便。 (4) 白噪声检验。对残差进行白噪声检验,由定义可知白噪声序列的任意两个时序值之间都是完全不相关的。但在实际中,完全的不相关是不可能的。由于序列的长度都是有限的,故自相关系数不可能都是零。可以认为自相关系数总是在零附近上下浮动,且浮动的范围有非常界限的序列为白噪声序列。为了定量准确的判断是否纯随机,Bartlett给出了统计的方法验证序列的白噪声性,此时是将自相关系数放在一起进行整体检验。Bartlett提出如果一个时间序列是白噪声序列,则提取一个观察个数为n的序列,那么该序列的延迟非零期的样本自相关系数将近似服从均值等于零,方差近似为观察序列个数倒数的正态分布。 (5) 预测。本文用Eviews6.0实现整个建模过程,Eviews软件是美国QMS公司推出的计量经济学软件,在对时间序列的数据进行分析,建立序列间的统计关系式,并用该关系式进行预测、模拟等。 图1为2011年1月~2012年11月我院实验室日常上机人数时序图,该时序图以天为单位,实验环境是Eviews6.0。由图1可以看出日常上机人数随机性很大, 观测值序列呈现周期性[16],可初步断定该序列为非平稳序列。 图1 日常上机人数时序图 为了进一步检验序列的平稳性, 本文对原序列进行ADF检验,即如果方程所有特征根都在单位圆内,则序列平稳,如果有一个特征根存在且为1,则序列为非平稳序列。ADF检验结果如表1所示。 由表1的结果可以看出,在10%的显著性水平下可以接受原假设,即原序列有一个单位根,故可以断定原序列具有非平稳性。 表1 ADF检验结果 从图1中可以看出,在每年的5月份和11月份都会有一段连续的峰值出现,表明此段时间内实验室上机人数较多。而8、2月份基本为零,因为这2个月为放假时间。可初步断定周期为6个月,有相关图可得周期为182天。 在一般情况下,周期性序列的季节性差分次数不会超过1[9]。因此,我们首先进行一阶差分消除趋势特征,再进行182步周期差分消除周期信息,并对差分后的序列进行ADF检验,结果如表2。 表2 差分序列ADF检验结果 由表2中的P值可以判断出,在10%的显著性水平下拒绝原假设,即序列对象不存在单位根。因而上机人数是1阶单整,故SARIMA模型的d=1。 通过差分后序列AC和PAC,判断SARIMA模型的阶数p、q、P、Q。由表3可以看出,AC 为一阶截尾,可令q=1。另外,在t=182处,PAC显著不为0,因此,可令P=1。同样观察偏相关系数,可以看出,p在8阶截尾,可得p=8。在t=182处,AC显著为0,因此,可令Q=0。 在EVIEWS 6.0中,对模型进行最小二乘法参数估计并利用模型对差分后的序列进行拟合,经过多次尝试、筛选和剔除所有不显著系数,最终确定结果见表4。 白噪声检验结果如表5所示。由表可知,AC与PAC显著趋于0,因而残差序列不存在自相关,是白噪声序列,故构建的模型是理想的,可用于预测。 表3 差分后序列相关图 表4 最小二乘法参数估计结果 表5 残差相关图 最终可得模型为ARIMA(8,1,1)(1,1,0),表4为相应参数的估计值。故模型方程为: (1-0.313B-0.268B2-0.151B7)(1+ 0.536B182)xt=(1-1.03B)εt 利用模型对2012年12月1日~15日进行预测。 由表6可以看出,预测结果比较接近实际情况。自2012年开始对模型进行研究,并应用于我院实验室开放实际中,一年以来,实验室开放管理水平得到了很大提升。在毫不影响学生充分利用实验室设备的基础上,为学院省下一部分财政支出,大大节约人、财、物的使用。减轻了工作人员的工作强度和工作时间。 ARIMA是一种计算简便、计算精度较高、使用范围很广的时间序列预测模型。季节性SARIMA 模型在原有模型的基础上扩展了对周期性序列的应用,使其范围更加广泛。本文利用季节性SARIMA模型,采用EVIEWS软件对实验室日常上机人数进行预测分析,是我院实验室开放管理的一部分,有效提高了实验室资源的利用率,方便学生学习,同时节省了资源,使我校的实验室管理水平又上了一个台阶。希望本研究对于其他学校实验室开放管理给予一个启发和借鉴。 表6 实际上机人数和预测人数对照表 [1] 蔡海燕,刘 昭.实验室信息化管理初探[J].实验室研究与探索,2010,29(11):373-375. CAI Hai-yan,LIU Zhao.Discussion on the Information Management of Laboratory[J]. Research and Exploration in Laboratory,2010, 29(11):373-375. [2] 王志军,杨延军.开放式教学实验室实时监控系统[J].实验室研究与探索,2011,30(1):158-160. WANG Zhi-jun,YANG Yan-jun. Real Time Monitoring System for Open Teaching Labs[J]. Research and Exploration in Laboratory,2011, 30(1):158-160. [3] Alon Gany. The role of laboratory experiments in engineering education [C]//Proc ASME 2008 9th Biennial Conference on Engineering Systems Design and Analysis (ESDA2008). Haifa, Israel, pp. July 2008:645-647. [4] Richard Chiou, Michael Mauk, William Danley, Robin Kizirian. Innovative engineering technology curriculum integrated with web-based technology in robotics, mechatronics, and equality [C]//Proc ASME 2009 International Mechanical Engineering Congress and Exposition (IMECE2009). Lake Buena Vista, Florida, USA, pp. 2009: 369-376. [5] Frank K. Lu, Philip K. Panicker, M. Byron Webb. Introducing modern laboratory experiences to mechanical and aerospace engineering students [C]//Proc ASME 2007 International Mechanical Engineering Congress and Exposition (IMECE2007). Seattle, Washington, USA, pp. 2007:443-452. [6] 王法玉,张 桦.基于Web 与短信结合的实验室开放管理系统设计与实现[J]. 实验技术与管理, 2011,28(1):104-107. WANG Fa-yu,ZHANG Hua. Design and Implementation of Laboratory Opening Management system based on Web and SMS[J]. Experimental Technology and Management,2011,28(1):104-107. [7] 金 旗,裴昌幸,朱畅华.ARIMA 模型法分析网络流量[J]. 西安电子科技大学学报(自然科学版),2003(2):6-10. JI Qi, PEI Chang-xing, ZHU Chang-hua. ARIMA analysis method in network traffic[J].Jouranl of Xidian University,2003(2):6-10. [8] 王宏禹. 非平稳随机信号分析与处理[M]. 北京: 国防工业出版社, 1999. 293-307. [9] 邹柏贤,刘 强.基于ARMA模型的网络流量预测[J].计算机研究与发展,2002,39(12):1645-1652. ZOU Bo-Xian, LIU Qiang. ARMA-BASED TRAFFIC PREDICATION AND OVERLOAD DETECTION OF NETWORK[J].Journal of Computer Research and Development, 2002,39(12):1645-1652. [10] 杨建萍. 基于ARIMA 模型的用电量时间序列建模和预报[J]. 工程数学学报, 2008,25(4): 611-615. YANG Jian-Ping. ARIMA Time Series Modeling and Forecasting of Electricity Consumption[J]. Chinese Journal of Engineering Mathematics, 2008,25(4): 611-615. [11] 漆 莉,李 革,李 勤. ARIMA 模型在流行性感冒预测中的应用[J]. 第三军医大学学报, 2007,29(3): 267-269. QI Li,LI Ge,LI Qin. Applications of ARMA model on predictive incidence of influenza[J].Acta Academiae Medicinae Militaris Tertiae, 2007,29(3): 267-269. [12] 韩 超, 宋 苏, 王成红. 基于ARIMA 模型的短时交通流实时自适应预测[J]. 系统仿真学报, 2004, 16(7): 1530-1532. HAN Chao,SONG Su,WANG Cheng.A Real-time Short-term Traffic Flow Adaptive Forecasting Method Based on ARIMA Model[J].Journal of System Simulation,2004,16(7): 1530-1532. [13] 周 鑫,张 锦,李 果,等.基于乘积季节模型的GPRS小区流量预测[J]. 计算机工程,2010,36(18):76-78. ZHOU Xin, ZHANG Jin, LI Guo,etc.Traffic Prediction of GPRS Cells Based on Multiple Seasonal Model[J].Computer Engineering,2010,36(18):76-78. [14] 张 蔚, 张彦琦, 杨 旭. 时间序列资料ARIMA 季节乘积模型及其应用[J]. 第三军医大学学报, 2002, 24(8): 955-957. ZHANG Wei,ZHANG YAN-qi,YANG Xu.Model of multiple seasonal ARIMA and its application ot data in time series[J]. Acta Academiae Medicinae Militaris Tertiae, 2002, 24(8): 955-957. [15] 张 伟, 张新波. 移动GSM网话务量的ARIMA模型的建立及其预测[J]. 数学理论与应用, 2008, 28(2): 70-74. ZHANG Wei, ZHANGXin-bo. Modeling and predicting wirless GSM traffic load on the ARIMA model[J].Mathematical Theory and Applications, 2008, 28(2): 70-74. [16] Geoge E,Box P. 时间序列分析预测与控制[M]. 顾岚主, 范金城,译. 北京: 中国统计出版社, 1997:125-126.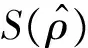
1.4 SARIMA模型建模步骤
2 实例应用
2.1 平稳性检验
2.2 周期性确定
2.3 平稳化处理
2.4 模型定阶
2.5 模型的建立与预测
3 结 语


