水溶液中染料吸光度与浓度的非线性关系

潘中达， 赵保丹， 周 进

(南京大学 固体微结构物理国家重点实验室，物理学院， 江苏 南京 210093)

0 引 言

溶液浓度的测量在化工、印染、制药、环保等行业中有着广泛的应用，通常有多种方法可以对溶液浓度进行测量，提高溶液浓度测量的精度，提出合理化的工作曲线模型，对生产生活与科研都有着重要的意义[1-4]。

利用分光光度计测出溶液的吸光度，通过对比该溶液的最大吸收峰处吸光度随浓度变化的标准工作曲线，是测出未知溶液浓度的一种常用的光度分析方法。在光度分析方法中有一条重要的定律——朗伯-比尔定律，在液层厚度等其他条件一致时，溶液的吸光度A=KC(K为比例系数；C为溶液浓度)，即吸光度与溶液浓度的关系是一条通过原点的直线[5]。但是朗伯-比尔定律的成立往往需要一系列苛刻的条件，实际测量过程中经常不容易满足而出现非线性偏离的现象。

我们在制定用吸光度方法测量一些溶液的染料浓度的工作曲线中，经常发现染料最大吸收峰处吸光度随浓度变化是非线性现关系，于是从分子间相互作用、折射率、染料的光稳定性3方面对该现象进行合理解释，并制定了大范围的吸光度与浓度关系的工作曲线，这些工作曲线可应用于精确测量和分析水溶液中染料的浓度。

1 实验部分

1.1 实验仪器和原料

实验仪器：电子天平；UV-1800PC紫外/可见分光光度计；CEL-HXUV300光催化氙灯光源；100～1 000 μL移液枪；石英比色皿1 cm路径。

原料：罗丹明B、天青1号、结晶紫、亚甲基蓝、荧光素、蒸馏水。

1.2 实验方法

分别准确称取一定量的罗丹明B、天青1号、结晶紫、亚甲基蓝、荧光素，溶于一定量体积的蒸馏水中，配成各自的不同浓度的水溶液。然后以水为基线，用1 cm路径石英比色皿，在400～700 nm波长范围内扫描各种溶液的吸收光谱。染料光降解实验是以石英比色皿为容器，用装有420～650 nm滤镜的氙灯以固定强度光照射已知吸光度的染料溶液一定时间。

2 实验结果

分别测量了天青1号，结晶紫，罗丹明B，荧光素，亚甲基蓝水溶液的吸收曲线，并拟合了它们最大吸收峰处的吸光度与浓度关系。结晶紫和罗丹明B的吸光度和浓度存在很好的线性正比例关系；然而对于低浓度(< 1.5 mg/L)和较高浓度(> 5 mg/L)的天青1号和亚甲基蓝，线性拟合会造成很大误差。特别是荧光素，吸光度的增加率始终随浓度的增加而减小。即在这些浓度区间，溶液浓度和吸光度表现出明显的非线性关系。为准确获得吸光度与浓度的关系，我们把天青1号分为3段进行拟合，在低浓度和较高浓度区内作非线性拟合，在中间浓度区间作线性拟合；而把亚甲基蓝分为两段进行拟合，发现荧光素和亚甲基蓝在测试的所有浓度区间都不能有效进行线性拟合。

2.1 天青1号水溶液最大吸收峰处A与浓度关系

图1(a)为各浓度天青1号溶液在400～700 nm波长范围内的吸收光谱，图1(b)为各浓度天青1号在最大吸收峰611 nm处的吸光度对浓度进行线性拟合后的结果。经过线性拟合的天青1号水溶液吸光度与溶液浓度的拟合度高达0.999，看似很高，但是我们发现它的截距有0.024 54，这就明显偏离了朗伯-比尔定律所要求的过原点的正比例关系。事实上，我们测得浓度C=0.8 mg/L的溶液的吸光度A=0.07，若根据上述获得的线性关系，用测得的吸光度计算得到的C′=0.56 mg/L，与真实浓度的误差达到了30%。

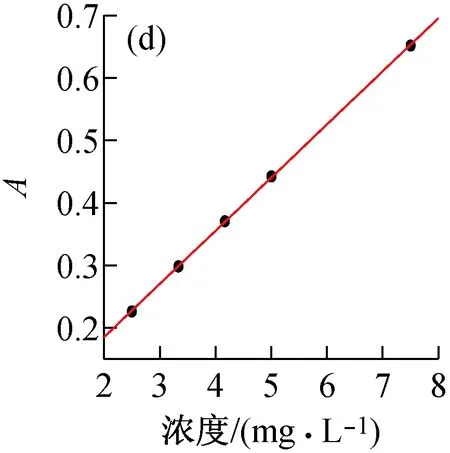
图1 天青1号水溶液的吸收光谱及最大吸收峰吸光度随浓度变化的拟合曲线

为增加拟合的准确性，我们将天青1号水溶液的吸光度与溶液浓度的关系分为如图1(c)～(e)的3段浓度区间进行拟合，其中(c)、(e)段为二次拟合，(d)段为线性拟合。进行上面所示浓度区间划分之后，拟合曲线对各点实际测量值的最大误差仅在2.5%之内。这说明了对于天青1号这种染料，朗伯-比尔定律仅在中间一部分浓度区间适用，溶液浓度很低或较高时，就会偏离朗伯-比尔定律，在精确度要求较高的测量中，必须对其进行非线性拟合。

2.2 结晶紫和罗丹明B水溶液的最大吸收峰处吸光度与浓度的关系

图2(a)为各浓度结晶紫溶液在400～700 nm波长范围内的吸收光谱，图2(b)为各浓度结晶紫在最大吸收峰583 nm处的吸光度对浓度进行线性拟合后的结果。图2(c)为各浓度罗丹明B溶液在400～700 nm波长范围内的吸收光谱，图2(d)为各浓度罗丹明B在最大吸收峰554 nm处的吸光度对浓度进行线性拟合后的结果。

图2 结晶紫和罗丹明B水溶液的吸收光谱及最大吸收峰吸光度随浓度变化的拟合曲线

由图2(b)和图2(d)可知，对于结晶紫和罗丹明B，在溶液浓度小于10 mg/L时，都能较好地符合朗伯-比尔定律，吸光度与浓度的工作曲线成正比例关系，尤其是结晶紫，所测点的实际值与计算值的最大相对误差小于2%。

2.3 荧光素和亚甲基蓝水溶液的最大吸收峰处吸光度与浓度的关系

图3(a)为各浓度荧光素溶液在350～700 nm波长范围内的吸收光谱，显然荧光素溶液随着浓度的变化，峰形发生变化。溶液浓度越高，最大吸收峰所在位置的波长越短。很明显，荧光素吸光度与浓度的工作曲线偏离了朗伯-比尔定律所要求的正比例关系，呈现出典型的非线性关系，故我们对各点进行二次拟合，见图3(b)。

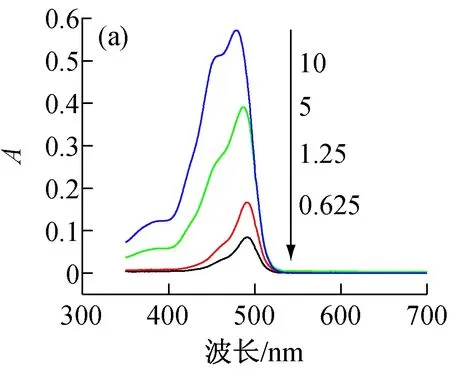
图3 荧光素水溶液的吸收光谱及最大吸收峰吸光度随浓度变化的拟合曲线

图4(a)为各浓度亚甲基蓝溶液在400～700 nm波长范围内的吸收光谱，图4(b)为各浓度亚甲基蓝在最大吸收峰665 nm处的吸光度对浓度进行线性拟合后的结果。由图4(a)可见，亚甲基蓝主峰明显，在其主峰旁有一较宽的肩部。随着溶液浓度的变化，它的峰形基本不变。

观察亚甲基蓝吸光度与浓度的工作曲线各点，可将其分两个浓度区间进行二次拟合，如图4(c)(二次拟合)，4(d)(二次拟合)所示。

3 吸光度与溶液浓度出现非线性现象的原因

我们认为，影响溶液吸光度与溶液浓度之间的线性关系有分子间的相互作用[6-9]、折射率[10-13]、染料的光稳定性等[14-16]，以下分别从这几个方面进行详细讨论。

3.1 分子间相互作用

朗伯-比尔定律是一个理想模型，它忽略了分子间的相互作用。然而，这些染料在水溶液中的相互作用是不能忽略的，不仅有染料分子间的相互作用，还有染料与水分子之间的相互作用。有色质点经常会发生缔合、离解、电离、溶剂作用和产生互变异构体等，从而导致吸收粒子相互间的平均距离发生变化，以致每个粒子都可影响其邻近粒子的电荷分布，这种相互作用可改变它们的吸光度[6]。

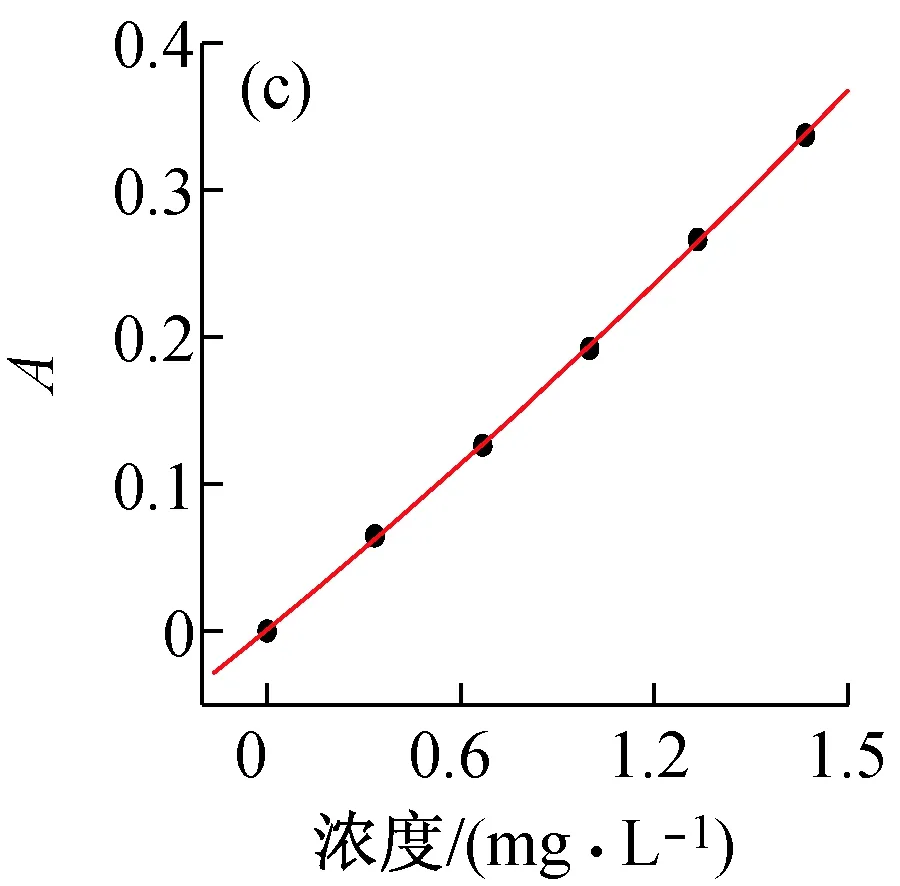
图4 亚甲基蓝水溶液的吸收光谱及最大吸收峰吸光度随浓度变化的拟合曲线

分子间相互作用对染料分子吸光度的影响通常会导致染料吸收光谱峰形的变化。如果2个分子距离过近，它们之间会有能量传输，即共振能量转移[7]，使得系统理化性质改变。当分子间的平均距离小于4.2 nm时(Förster distance)，共振能量转移的效率将超过50%[8]。因为共振能量转移的存在，当溶液浓度增加时，最大吸收峰处吸光度的增长率会变低，甚至使吸收峰峰形发生变化。由于我们所使用荧光素的相对分子质量为333.31 g/mol，假设分子独自占据一小正方体的空间，可计算得，当分子间平均距离为4.2 nm时，溶液浓度约为7.45 mg/L。由于计算时未计入分子本身体积，所以实际所需浓度可能更小。再由图3(a)中，主峰左侧的肩部说明荧光素在水溶液中并不是以单个分子或单个离子的形式存在，有一部分以二聚体的的形式存在，溶液浓度越大二聚体的浓度也越大[9]。以上这些原因导致荧光素溶液在浓度5～10 mg/L时，吸光度的增加率有明显的减小。

3.2 折射率

朗伯-比尔定律认为吸光度与浓度成正比，是建立在摩尔吸光系数ε定值的基础上的，然而ε并非一个定值，而是真实吸光系数ε真和溶液的折射率n的函数：

随着浓度的增大，折射率的变化已经不能忽略。根据文献[10-13]，可从光与物质的相互作用关系,求得溶液浓度与其折射率关系的理论模型。当溶液的浓度较小且作用于溶液的光场频率为一常数时，溶液的浓度与其折射率近似成线性关系，即可以写为：c=an+b。式中：a，b为常系数；c为溶液的浓度；n为溶液的折射率。

水的折射率为1.333，当溶液折射率在百分位有变化时，吸光系数就会有相对1%的变化，对ε函数式求导可得吸光系数在n2> 2/3时单调递减，因此吸光度随浓度变化的曲线在浓度偏大的一段有负偏离的趋势。这就很好地解释了天青1号、亚甲基蓝在高浓度区间，随着溶液浓度的增加，吸光度的增加比率相对减小的现象。

3.3 染料的光稳定性

一般来说，染料分子对近紫外和可见光区的光吸收是由于价电子跃迁引起的，是量子化的，而且染料对光的选择性吸收的性质与染料分子能量、染料所吸收光子的能量有关。

不管怎样，根据能量守恒定律，染料吸收的光能都将转化为其他形式的能量，一定强度的光照射下染料的性质和结构会发生变化，这就是我们在配置染料后都会密封避光保存的原因。不同结构的物质对于光的稳定性不同，而分光光度法的测量本身也需要光源，我们认为，如果所测染料对光的稳定性较差，那么在用分光光度计测量时，虽然不至于使染料变性分解，但也必定会影响吸光度的值[14-16]。

我们取吸光度约为1.0(见表1)和0.5(见表2)的各染料，石英比色皿为容器，分别在装有420～650 nm滤镜的氙灯下以相同强度光照射10 min，从图5和表1中可以看出，经过照射，各种染料都发生了明显的光降解现象(这里的降解率指的是吸光度降低的百分比)。比较表1和表2，可知相同条件下浓度低的染料通常降解率大。

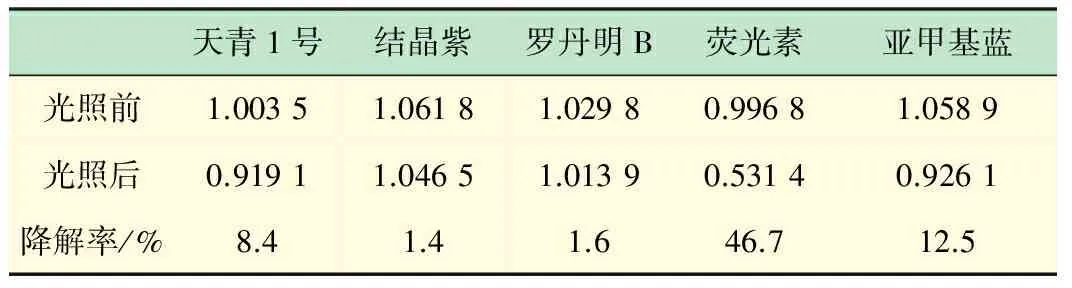
表1 初始吸光度约为1.0的染料在光照前后的吸光度值

注：降解率大于5%的可在图中明显表示

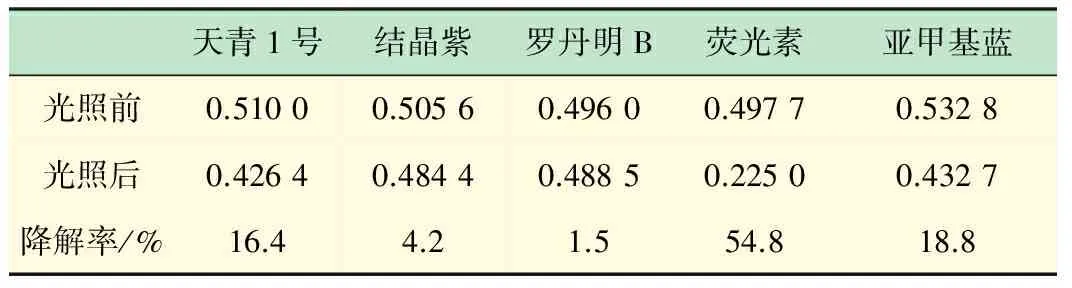
表2 各初始吸光度约为0.5的染料在光照前后的吸光度值

以上结果表明：

(1) 荧光素的光稳定性最差，对应于它的工作曲线的非线性性质最明显，而结晶紫和罗丹明B的光稳定性较好，它们在浓度10 mg/L以下呈现很好的线性性质，符合朗伯-比尔定律要求的正比例关系。

(2) 随着浓度的降低，经过相同时间同种光强照射的染料溶液的降解率一般会增加。对于天青1号和亚甲基蓝而言，它们本身就是光降解明显的染料，在低浓度区间这种降解更加显著，这便解释了这类染料在低浓度区间吸光度和浓度的关系呈现出开口向上的二次曲线现象的原因。

(a) 天青1号

(b) 荧光素

(c) 亚甲基蓝

4 结 论

通过研究大浓度范围内的多种染料水溶液(包括天青1号，结晶紫，罗丹明B，荧光素和亚甲基蓝水溶液)的吸光度与浓度之间的关系，得出以下结论。

(1) 朗伯-比尔定律能够近似地解释染料吸光度与浓度之间的关系。

(2) 由于分子间相互作用、折射率和光稳定性等因素，染料吸光度和浓度之间在浓度较大或较小时呈现非线性关系，尤其是分子间相互作用明显、光稳定性较差的荧光素，这种非线性现象表现得最为明显。

(3) 在运用分光光度法进行实际测量时，必须明确工作曲线的适用区间，尤其在低浓度和高浓度时，必须根据所需精度，拟合合适的工作曲线进行测量计算。

致谢感谢章建辉老师的指导。

[1] 杨燕婷，王 敏，周 莹，等. 超声光栅测量溶液中超声声速与浓度关系研究[J]. 实验技术与管理，2011,28(7):32-35.

YANG Yan-ting, WANG Min, ZHOU Ying,etal. Study on relationship between sound velocity of ultrasonic wave and solution concentration measured by ultrasonic diffraction[J]. Experimental Technology and Management, 2011,28(7):32-35.

[2] 于莲芝，崔晓钰，佘国君，等. LiBr溶液浓度自动测量系统研制[J]. 实验室研究与探索，2010,29(1):6-8.

YU Lian-zhi, CUI Xiao-yu, SHE Guo-jun,etal. Development of the automatic measurement system of LiBr liquor concentration[J]. Research and Exploration in Laboratory, 2010,29(1):6-8.

[3] 金清理. 基于掠入射法溶液浓度测量系统研究[J]. 光子学报，2006,35(1):138-141.

JIN Qing-li. Study of solution concentration measurement system based on a method of glancing incidence[J]. Acta Optica Sinica, 2006,35(1):138-141.

[4] 牛法富，赵继飞，孟军华，等. 利用核磁共振测量乙醇汽油溶液浓度[J]. 物理实验，2011,31(11):37-39.

NIU Fa-fu, ZHAO Ji-fei, MENG Jun-hua,etal. NMR Characterization of ethanol-gasoline[J]. Physics Experimentation, 2011,31(11):37-39.

[5] 殷海青. 光度分析中工作曲线偏离朗伯—比尔定律的原因[J]. 青海师专学报，2004(5):63-66.

YIN Hai-qing. A discussion on work curve deviate the law of Lambert-Beer in the spectrum analysis[J]. Journal of Qinghai Junior Teachers’ College, 2004(5):63-66.

[6] 曹 晖. 偏离朗伯—比耳定律的有关问题[J]. 黔东南民族师范高等专科学校学报，2004,22(3):17-19.

CAO Hui. Study on work curve deviate the law of Lambert-Beer[J]. Journal of Southeast Guizhou National Teachers’ College, 2004,22(3):17-19.

[7] Zhang J H, Thurber A, Tenne D A,etal. Enhanced dye fluorescence in novel Dye-ZnO nanocomposites[J]. Adv Funct Mater, 2010,20:4358-4363.

[8] Lakowicz J R, Malicka J, D’Auria S,etal. Release of the self-quenching of ?uorescence near silver metallic surface[J]. Analytical Biochemistry, 2003,320,13-20.

[9] 毕只初. 荧光素水溶液的吸收光谱和荧光光谱研究及可能的运用[J]. 化学试剂，1986,8(6):324-327.

BI Zhi-chu. Study of aborption and fluorescence spectra of fluorescein in aqueous solutions and its possible application[J]. Huaxue Shiji, 1986,8(6):324-327.

[10] 张志伟，尹卫峰，温廷敦，等. 溶液浓度与其折射率关系的理论和实验研究[J]. 中北大学学报(自然科学版)，2009,30(3):281-285.

ZHANG Zhi-wei, YIN Wei-feng, WEN Ting-dun,etal. Study on the relational expression of solution concentration and Its refractive index[J]. Journal of North University of China (Natural Science Edition), 2009,30(3):281-285.

[11] 戴新宇，闫长春，王 群. 动态判别溶液浓度大小的光电测量方法[J]. 实验室研究与探索，2004,23(12):27-28.

DAI Xin-yu, YAN Chang-chun, WANG Qun. A novel photoelectric measurement method for differentiating the solution concentration[J]. Research and Exploration in Laboratory, 2004,23(12):27-28.

[12] 曾 捷，梁大开，曾振武，等. 基于SPR光谱分析的液体折射率测量研究[J]. 光谱学与光谱分析，2006,26(4):723-727.

ZENG Jie, LIANG Da-kai, ZENG Zhen-wu,etal. Study on measurement of liquid refractive index by analyzing SPR spectrum character[J]. Spectroscopy and Spectral Analysis, 2006,26(4):723-727.

[13] 白泽生，刘竹琴，徐 红. 几种液体的折射率与其浓度关系的经验公式[J]. 延安大学学报(自然科学版)，2004,23(3):33-34.

BAI Ze-sheng, LIU Zhu-qin, XU Hong. An experienced formula about the connection of refraction index and consistence of several liquid[J]. Journal of Yanan University (Natural Science Edition), 2004,23(3):33-34.

[14] 庄德华，陈春宇，张栗源，等. 染料在光照时发生的化学反应及褪色产物[J]. 染料与染色，2007,44(5):33-37.

ZHUANG De-hua, CHEN Chun-yu, ZHANG Li-yuan,etal. The photo-induced reactions of dyes and their fading products[J]. Dyestuffs and Coloration, 2007,44(5):33-37.

[15] 杨松杰，孟凡顺，陈孔常，等. 菁染料和份菁染料的合成及其溶液的光稳定性研究[J]. 感光科学与光化学，2001,19(3):185-192.

YANG Song-jie, MENG Fan-shun, CHEN Kong-chang,etal. Synthesis and photostability of cyanine and merocyanine dyes solution[J]. Photographic Science and Photochemistry, 2001,19(3):185-192.

[16] 唐炳涛，张淑芬，徐 华，等. 高分子染料的光稳定性研究[J]. 染料与染色，2008,45(4):16-22.

TANG Bing-tao, ZHANG Shu-fen, XU Hua,etal. A study on the photostabilization of polymeric Dye[J]. Dyestuffs and Coloration, 2008,45(4):16-22.