稳态法测量导热系数的误操作影响分析

柯 磊， 杨党强， 袁艳红

(上海电机学院 数理研究所， 上海 201306)

0 引 言

导热系数是表征物质热传导性质的物理量，材料的导热系数与材料的组分和结构有关，通常需要采用实验的方法精确确定[1-4]。稳态法测量不良导体的导热系数的目的是让学生应用稳态法进行导热系数的测量，同时学习用物体的散热速率求传导速率的实验方法[5-8]。但我们在近些年的实验教学过程中发现，学生在实验操作中，出现了一系列误操作行为，导致测量的导热系数产生较大偏差。本文模拟实验中一些常见的误操作，并对大量实验结果进行系统的比较，分析引起导热系数出现偏差的主要因素，为实验教学提供参考。

1 稳态法测量导热系数

1898年，Lees首先使用平板法测量不良导体的导热系数。实验中，样品制成平板状，其上端面与一个稳定的均匀发热体充分接触;下端面与一均匀散热体相接触。由于平板样品的侧面积比平板面积小很多，可以认为热量只沿着上下方向垂直传递，横向由侧面散去的热量可以忽略不计，即可以认为，样品内只有在垂直样品平面的方向上有温度梯度，在同一平面内，各处的温度相同[9-10]。

设稳态时，样品上、下平面温度分别为θ1、θ2，根据傅里叶传导方程[11]，在Δt内通过样品的热量ΔQ为

(1)

式中：λ为样品的导热系数；h0为样品的厚度；S为样品的平面面积；实验中样品为圆盘状，直径为D。

图1为稳态法测量导热系数的示意图，当传热达到稳定状态时，样品上下表面的θ1和θ2不变，这时可以认为加热盘通过样品传递的热流量与散热盘向周围环境的散热量相等[12]。因此，可以通过散热盘在稳定温度θ2时的散热速率来求出热流量：

式中:m为散热盘的质量;c为散热盘的比热容。

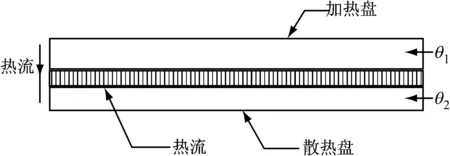
图1 稳态法测量导热系数示意图

在达到稳态过程中，散热盘的上表面并未暴露在空气中，而物体的冷却速率与它的散热表面积成正比，故稳态时散热盘散热速率表达式应作面积修正[13]：

(2)

式中:R为散热盘的半径;h为散热盘的厚度。

由式(1)、(2)可得样品的导热系数为

(3)

2 误操作影响分析

在实际的实验教学中发现，不少学生存在实验误操作，导致测量的导热系数出现偏差，主要误操作包括：样品与加热、散热盘未对齐；样品与加热、散热盘接触过紧；未达到稳态时测试；未进行强迫对流换热；热电偶与加热、散热盘接触不充分等。本文将模拟上述误操作，分析稳态法实验中误操作对测量的导热系数数值的影响。

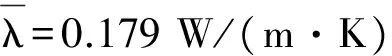
2.1 样品与加热、散热盘未对齐

学生操作时最常见的一类误操作是未将橡皮样品与加热、散热盘对齐，通常未对齐的表面积比例在10%以内。分别将橡皮样品与两盘未对齐比例设置在5%和10%，并设置极端比例50%进行误操作对比实验，实验曲线如图2所示。从图2可见，未对齐实验的曲线和参考曲线相比出现了明显的偏移，在散热盘稳态温度附近的曲率存在一定的偏差。结合表1实验数据，随着样品与两盘未对齐比例的增加，散热盘稳态温度和导热系数均逐渐下降；在常见的未对齐比例10%的实验中，导热系数的百分差为6.7%，偏差较大。

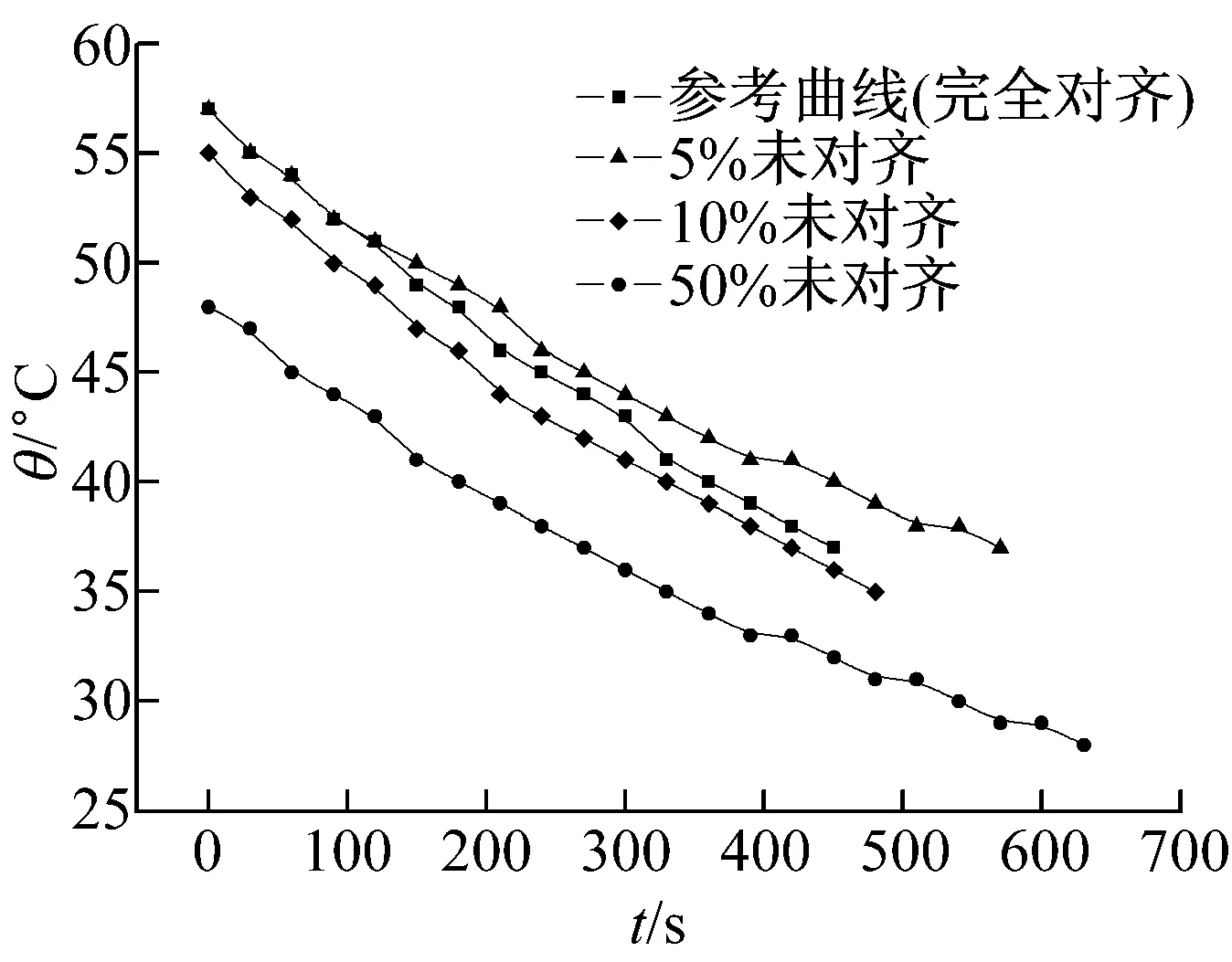
图2 样品与加热、散热盘未对齐对比实验曲线

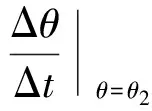
2.2 样品与加热、散热盘接触过紧

为了定量模拟样品与加热、散热盘接触过紧的误操作，采取在加热盘上方添加砝码的方式。实验中，添加的砝码质量分别为0.5、1.0、2.0 kg，3组实验数据高度一致。仅以2.0 kg的额外压力为例来分析样品与两盘接触过紧的误操作，实验曲线如图3所示。从图3可见，压力实验的曲线和参考曲线在散热盘稳态温度附近的曲率较一致，表1中实验数据表明，导热系数的百分差为2.2%，偏差较小。这也表明，2 kg以内的额外压力对实验的影响不大，样品的导热系数误差较小。

2.3 未达到稳态时测试

在操作中未达到稳态时测试也是较常见的一类误操作。根据稳态法的原理，必须得到稳定的温度分布，这就需要较长的时间等待。不少学生在实验中缺乏耐心，在散热盘的温度尚未稳定便进行数据的采集和记录。图4为未达到稳态时测试实验的对比曲线图，图中分别模拟了低于稳态温度1、2、3 ℃的实验结果。从图中可以看出，虽然未达到稳态时测试的曲线相对于参考曲线的偏移不是很大，但在散热盘稳态温度附近的曲率有明显的偏差。结合表1中的实验数据，随着散热盘稳态温度的降低，样品导热系数大幅度下降；当散热盘稳态温度为44 ℃时，样品的导热系数降低到0.115 W/(m·K)，降低了35.8%，偏差非常大。

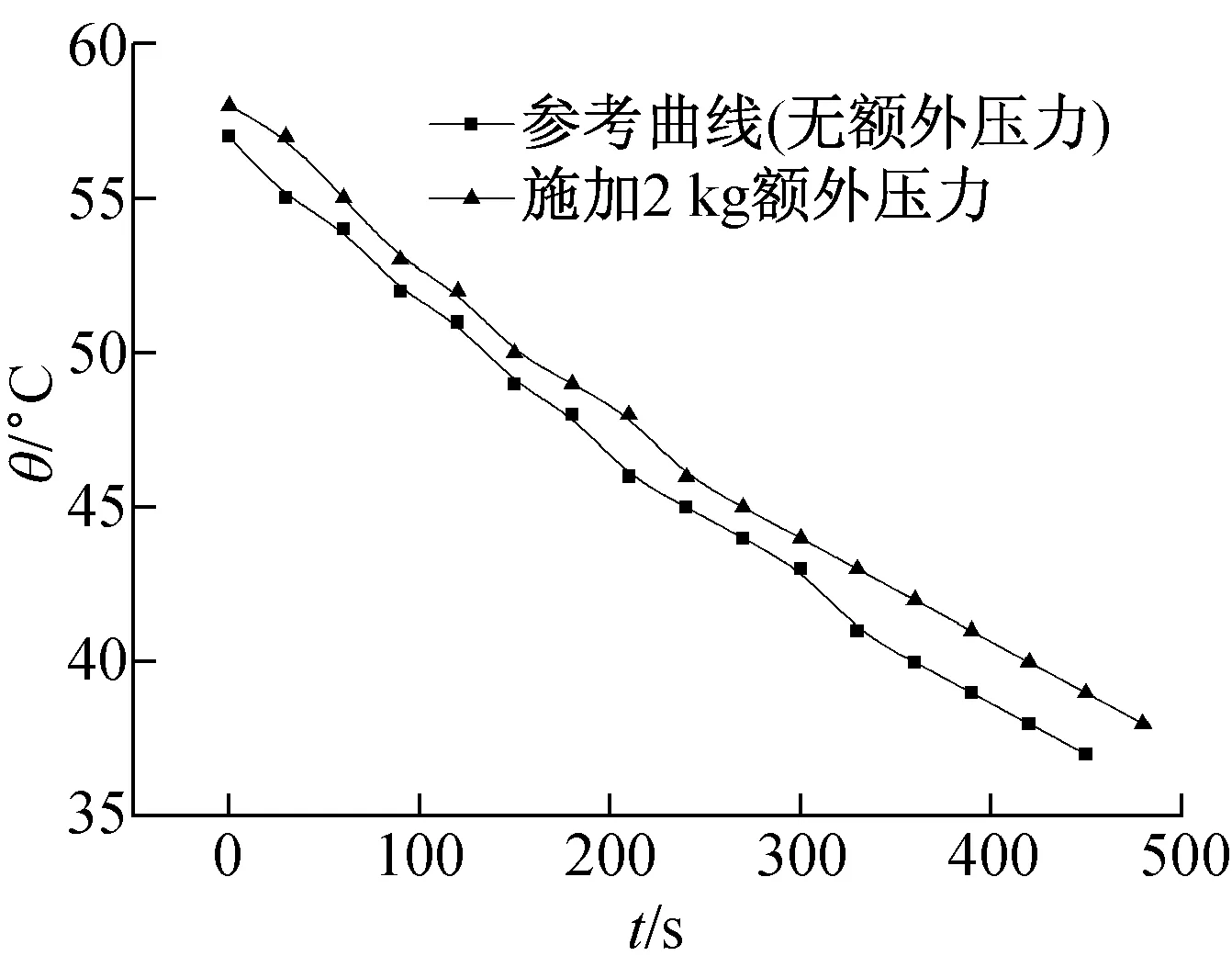
图3 样品与加热、散热盘接触过紧对比实验曲线

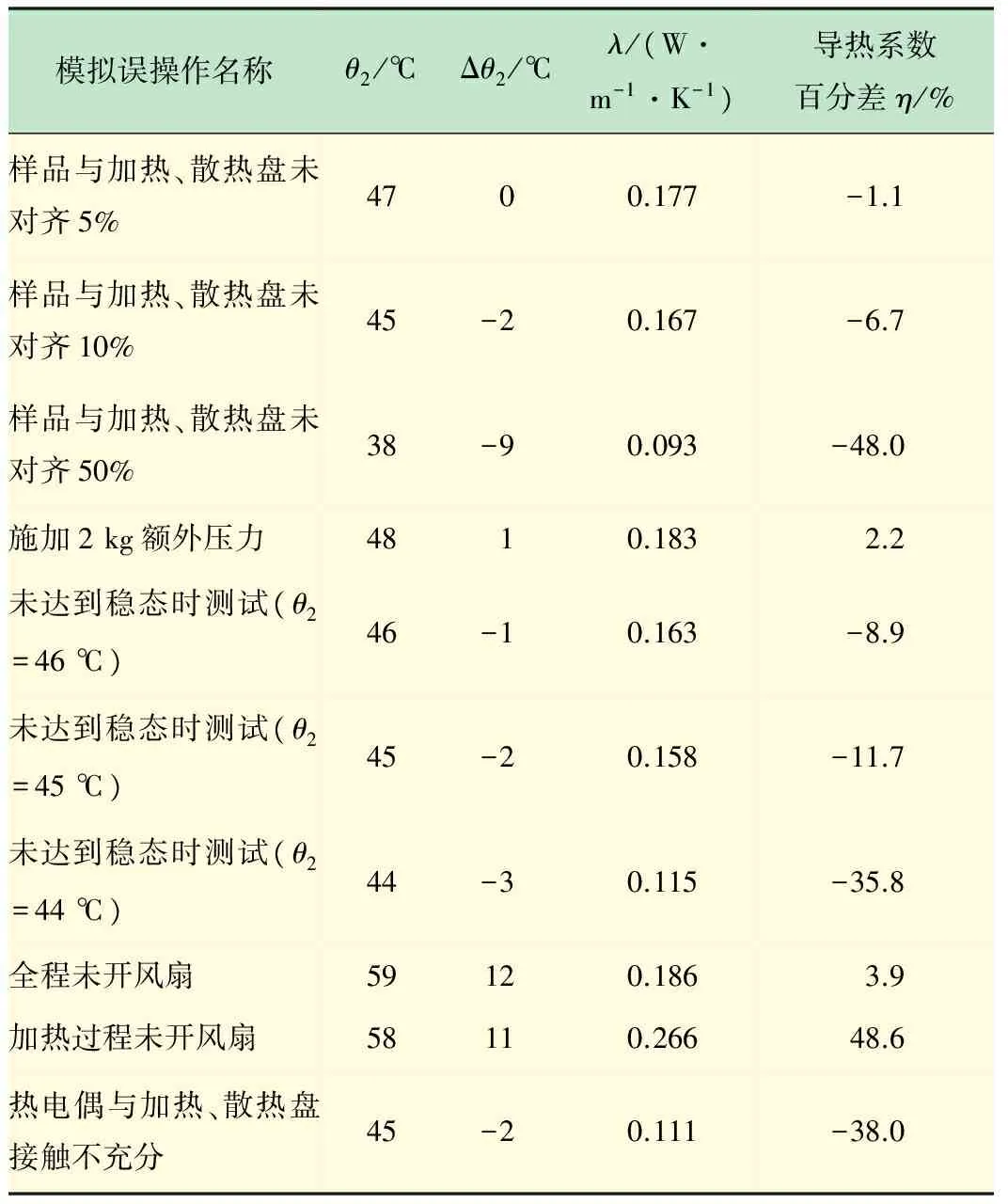
模拟误操作名称θ2/℃Δθ2/℃λ/(W·m-1·K-1)导热系数百分差η/%样品与加热、散热盘未对齐5%4700．177-1．1样品与加热、散热盘未对齐10%45-20．167-6．7样品与加热、散热盘未对齐50%38-90．093-48．0施加2kg额外压力4810．1832．2未达到稳态时测试(θ2=46℃)46-10．163-8．9未达到稳态时测试(θ2=45℃)45-20．158-11．7未达到稳态时测试(θ2=44℃)44-30．115-35．8全程未开风扇59120．1863．9加热过程未开风扇58110．26648．6热电偶与加热、散热盘接触不充分45-20．111-38．0

注：负值表示低于参考值

未达到稳态时测试，一方面使温差θ1-θ2增加，另一方面较低的θ2值引起散热盘稳态点向低温处偏移，曲率(Δθ/Δt)|θ=θ2减小，这两方面都会导致导热系数降低。

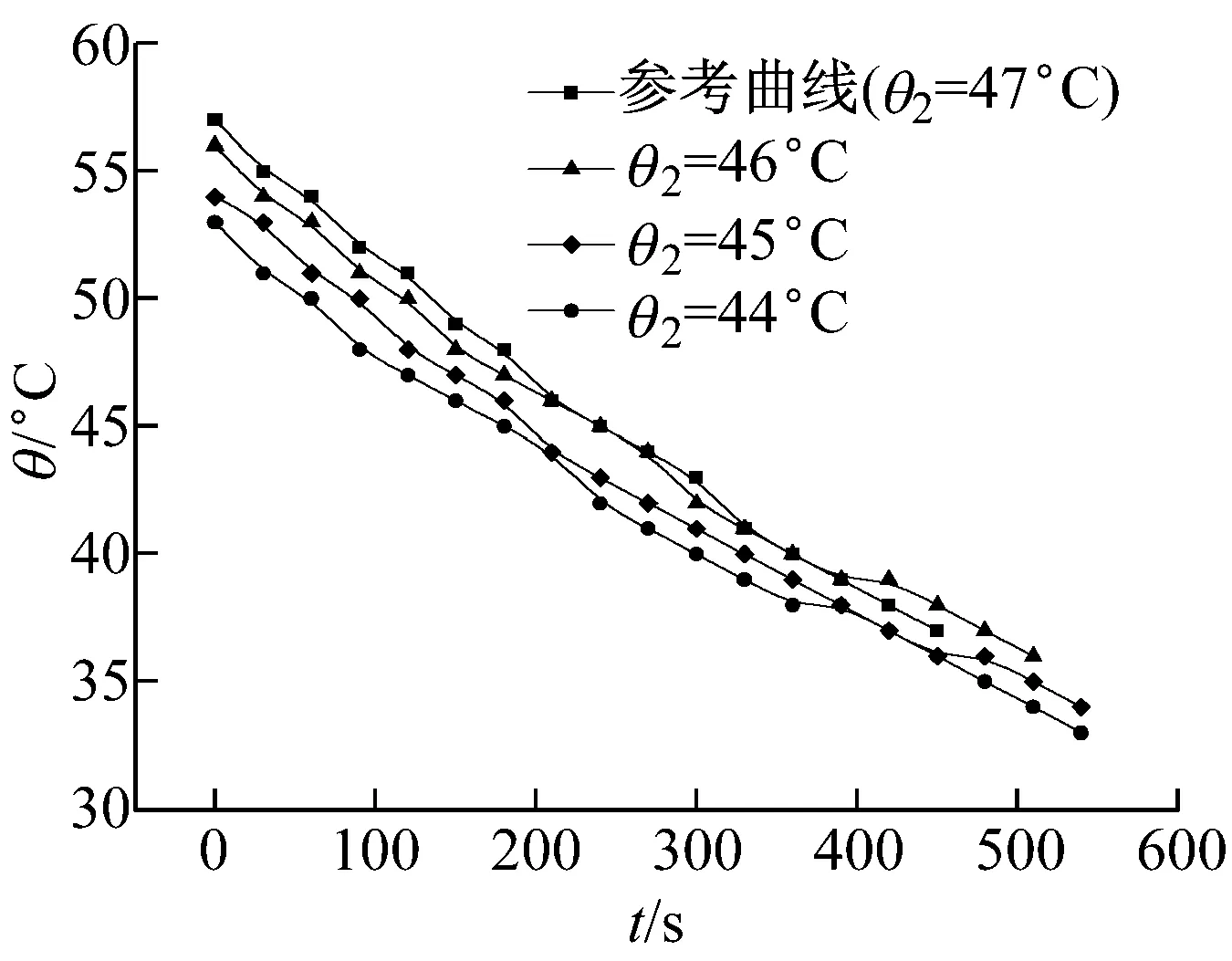
图4 未达到稳态时测试对比实验曲线

2.4 未进行强迫对流换热

在分析未进行强迫对流换热对实验的影响时，采取两种不同的方式进行：全程未开风扇、加热过程未开风扇。这两种方式分别模拟整个实验过程忘记进行强迫对流换热，以及实验过程中记起后再进行强迫对流换热的情况，实验曲线如图5所示。从图5可见，两种方式均对实验结果造成了影响，使曲线向高温方向产生了较大的偏移。从表1的实验数据中可以看出，两种方式使散热盘的稳态温度值升高了11～12℃，其中全程未开风扇引起导热系数的百分差只有3.9%，而加热过程未开风扇对导热系数的影响很大，百分差达到48.6%。

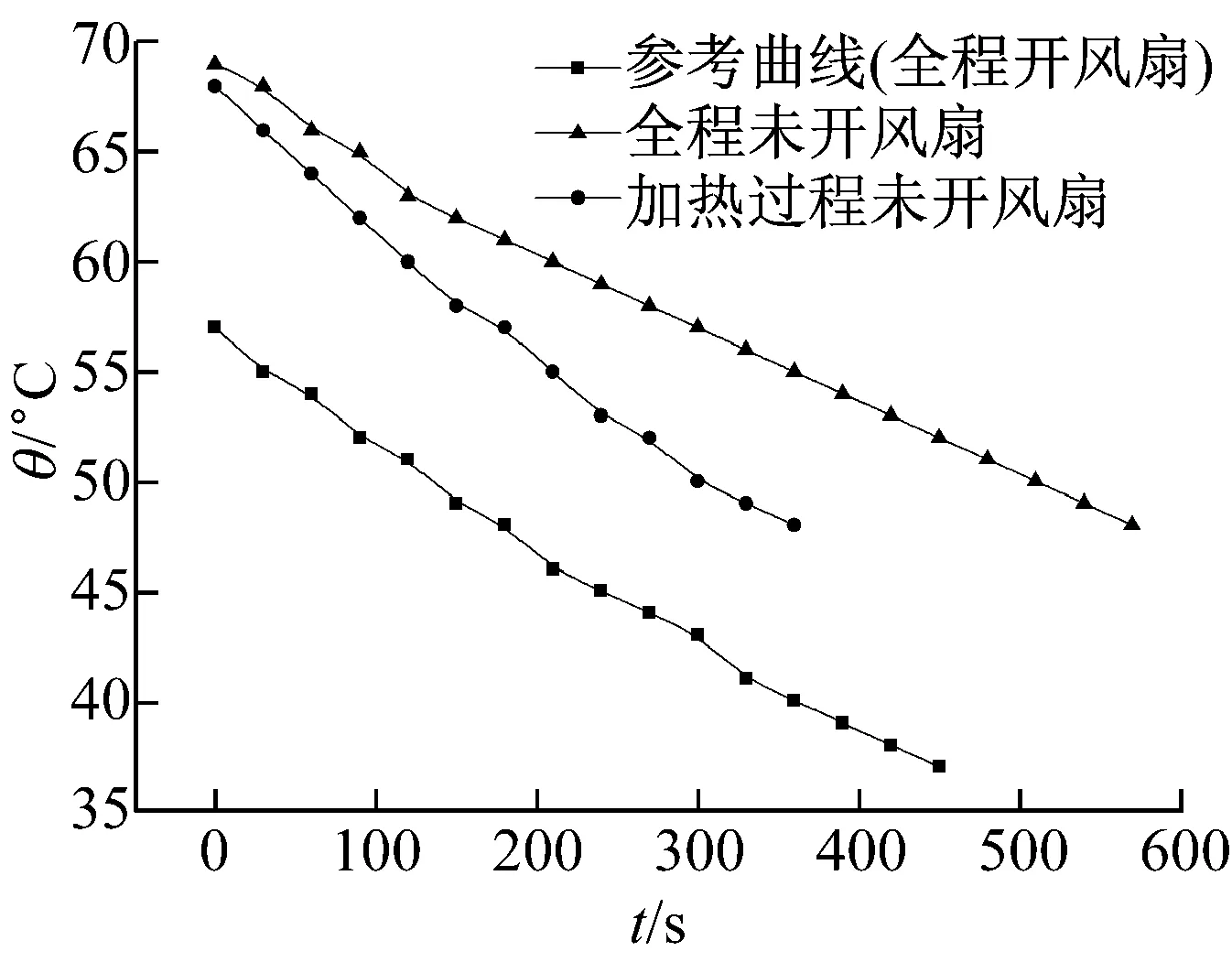
图5 未进行强迫对流换热对比实验曲线

造成上述偏差的原因同样可以从温差θ1-θ2的变化和散热盘稳态点处曲率(Δθ/Δt)|θ=θ2的变化两方面来分析。全程未开风扇和加热过程未开风扇均会使散热盘的稳态温度θ2升高，因此温差θ1-θ2减小，导热系数变大。然而，全程未开风扇的散热过程变缓，散热盘稳态点处的曲率(Δθ/Δt)|θ=θ2减小，导热系数变小，缩小了温差引起的偏差；而加热过程未开风扇的散热过程较快，曲率(Δθ/Δt)|θ=θ2较大，导热系数变大，加剧了温差引起的偏差。

2.5 热电偶与加热、散热盘接触不充分

实验中需在热电偶上均匀涂抹硅脂[15]，并要求插到加热、散热盘洞孔底部，以保证接触良好，提高测试的准确性。但是不少学生忽略了这一点，在实际操作中经常出现热电偶的硅脂涂抹部分裸露在两盘洞孔外。将热电偶搭在两盘的边缘模拟接触不充分的实验操作，实验曲线如图6所示。从图6可见，热电偶接触不充分曲线和参考曲线位置比较接近，但曲线斜率偏差较大。从表1中的实验数据可以看出，散热盘的稳态温度为45℃，但是导热系数百分差为38.0%，偏差非常大。热电偶与两盘接触不充分，导致测试灵敏度降低，测得的散热盘温度变化数据变缓，曲率(Δθ/Δt)|θ=θ2减小，计算出的导热系数值偏低。

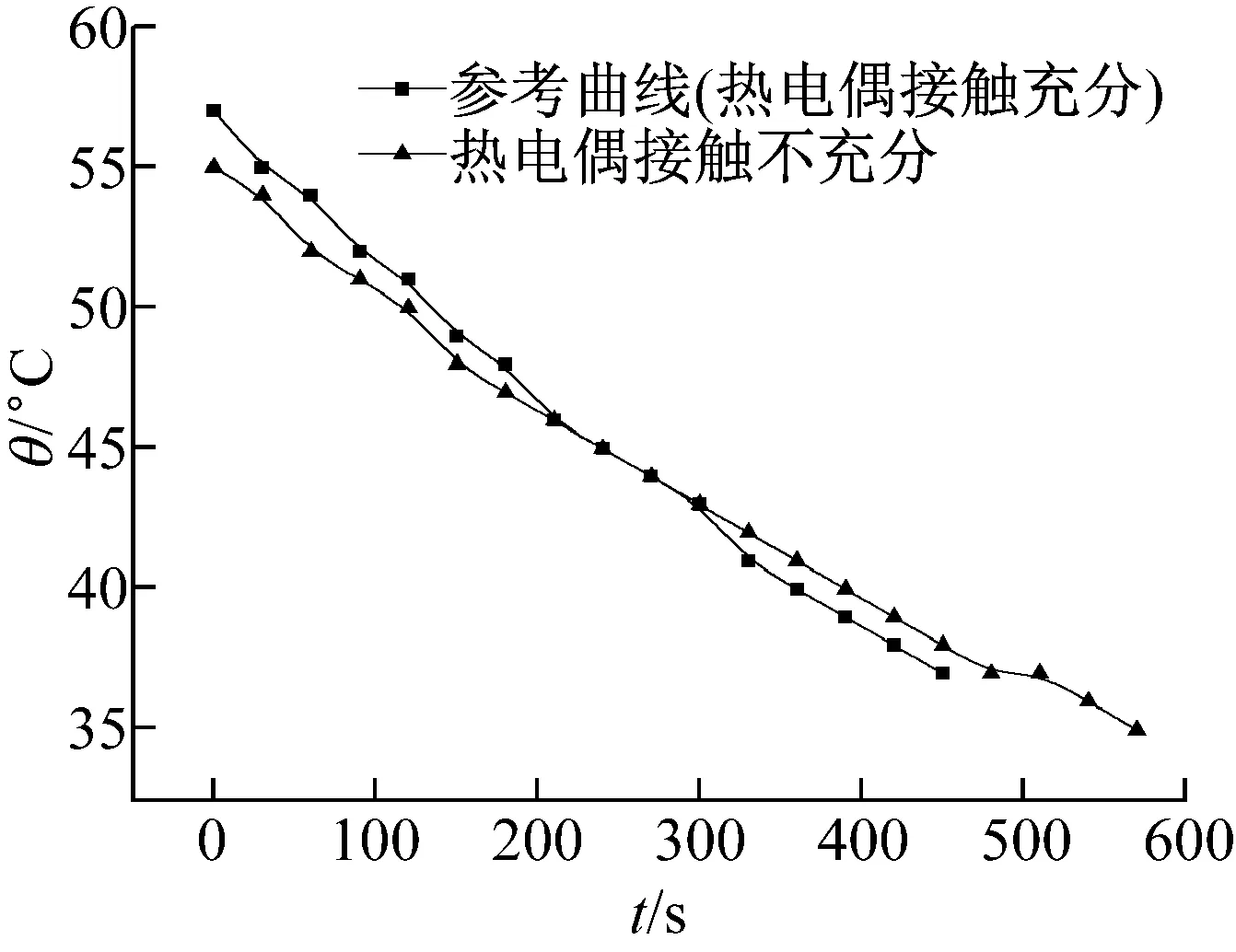
图6 热电偶与加热、散热盘接触不充分对比实验曲线

3 结 语

上述稳态法测量导热系数的模拟误操作实验表明，误操作影响散热盘的稳态温度和样品的导热系数。其中，样品与两盘未对齐10%时，散热盘稳态温度降低2℃，导热系数减小6.7%；施加2 kg额外压力时，散热盘稳态温度升高1℃，导热系数增大2.2%；散热盘稳态温度降低3℃时，导热系数减小35.8%；加热过程未开风扇时，散热盘稳态温度升高11℃，导热系数增大48.6%；热电偶与两盘接触不充分时，散热盘稳态温度降低2℃，导热系数减小38.7%。实验中，误操作对两盘的温差θ1-θ2和以及散热盘稳态点处的曲率(Δθ/Δt)|θ=θ2影响较大。在未达到稳态时测试、热电偶与两盘接触不充分的误操作中，散热盘稳态点处的曲率(Δθ/Δt)|θ=θ2大幅减小，导致导热系数明显减小；在加热过程未开风扇的误操作中，散热盘的稳态温度以及稳态点处的曲率(Δθ/Δt)|θ=θ2均有大幅增加，导致导热系数明显增大。

[1] 朱亚彬, 成正维, 刘依真. 对不良导体导热系数测量实验的改进[J]. 大学物理, 2004, 23(4): 25-27.

Zhu Ya-bin, Cheng Zheng-wei, Liu Yi-zhen. The improvement of the experiment for thermal conductivity of poor conductor[J]. College Physics, 2004, 23(4): 25-27.

[2] 杨永华, 曾 辉, 陈美华. 改进型导热系数测量仪的研制与实验[J]. 实验室研究与探索, 2011, 30(3): 20-23.

Yang Yong-hua, Zeng Hui, Chen Mei-hua. Development and experiment of improved thermal conductivity measurement instrument

[J]. Research and Exploration in Laboratory , 2011, 30(3): 20-23.

[3] 孙庆龙, 王玉梅. 利用稳态法测定不良导体的导热系数[J]. 计量与测试技术, 2010, 37(10): 69-70.

Sun Qing-long, Wang Yu-mei. Measuring the thermal conductivity of poor conductor by using the steady state method[J]. Metrology and Measurement Technique, 2010, 37(10): 69-70.

[4] 解俊梅, 田淑英, 侯方卓. 稳态圆筒法测定材料的导热系数[J]. 实验室研究与探索, 1997, 16(3): 42-45.

Xie Jun-mei, Tian Shu-ying. Measuring the thermal conductivity by using the steady cylinder method[J]. Laboratory Research and Exploration, 1997, 16(3): 42-45.

[5] 张建智, 周孑民, 章世斌. 稳态圆筒壁法自动测量颗粒导热系数的改进[J]. 有色金属, 2004, 56(4): 146-149.

Zhang Jian-zhi, Zhou Jie-min, Zhang Shi-bin. Improvement of particle thermal conductivity automatic measuring with steady cylinder method[J]. Nonferrous Metals, 2004, 56(4): 146-149.

[6] 周其云. 溶液导热系数测定仪的研制[J]. 实验室研究与探索, 1996, 15(3): 60-61.

Zhou Qi-yun. Development of the instrument for measuring the solution thermal conductivity[J]. Laboratory Research and Exploration, 1996, 15(3): 60-61.

[7] 李丽新, 刘圣春, 刘秋菊. 用综合测量方法设计固体导热系数测试实验台[J]. 实验室研究与探索, 2006, 25(4): 435-438.

Li Li-xin, Liu Sheng-chun, Liu Qiu-ju. Design of thermal conductivity test desk for solid materials with multi-measuring method[J]. Research and Exploration in Laboratory, 2006, 25(4): 435-438.

[8] 贾斐霖, 李林, 史庆藩. 稳态法测算导热系数的原理[J]. 材料科学与工程学报, 2011, 29(4): 609-613.

Jia Fei-lin, Li Lin, Shi Qing-fan. Principle of measuring thermal conductivity based on steady-state method[J]. Journal of Materials Science and Engineering, 2011, 29(4): 609-613.

[9] 冯毅, 梁满兵. 稳态平板导热系数测定仪的误差分析[J]. 广州化工, 2006, 34(1): 56-59.

Feng Yi, Liang Man-bing. Error analysis on the stable flat measuring instrument for thermal conductivity[J]. Guangzhou Chemical Industry, 2006, 34(1): 56-59.

[10] 李锋, 邓刚锋. 基于LabVIEW的不良导体导热系数测量系统[J]. 计算机测量与控制, 2009, 17(10): 1928-1930.

Li Feng, Deng Gang-feng. Measuring system of thermal conductivity of poor conductor based on LabVIEW[J]. Computer Measurement and Control, 2009, 17(10): 1928-1930.

[11] 杨世铭, 陶文栓. 传热学[M]. 北京: 高等教育出版社, 2000.

[12] 吴铁山, 李道银. 大学物理实验[M]. 武汉: 湖北科学技术出版社, 2005.

[13] 徐福新, 刘碧兰. 大学物理实验[M]. 长沙: 中南大学出版社, 2011.

[14] 杨党强, 吴纲, 金亚平. 大学物理实验[M]. 北京: 中国电力出版社, 2009.

[15] 赵法刚, 王云霞. 保温材料导热系数的自动化测量[J]. 自动化与仪表, 2009, 24(1): 48-50.

Zhao Fa-gang, Wang Yun-xia. Thermal conductivity automatic measurement of insulated materials[J]. Automation and Instrumentation, 2009, 24(1): 48-50.