基于改进的数学形态学边缘检测算法研究

王东霞, 许伟昶

(济源职业技术学院,河南 济源 459000)

0 引 言

图像边缘一般是指图像中像素灰度有阶跃变化或屋顶状变化的那些像素的集合，可以粗略地分为阶跃边缘和屋顶边缘，它存在于目标与背景、目标与目标、区域与区域、基元与基元之间[1]。边缘检测在图像预处理中有非常大的作用，其在图像处理及人脸识别等方面的应用也是非常广泛。目标对象的轮廓可以被它清晰的描绘出来，所含概的信息量非常大，如阶跃性质、形状等，使读者清晰明了。在边缘检测算法研究中，提出了比较多的检测算法，如: Sobel算子﹑Canny算子[2]和梯度算子等，但这些算法通常较难得到良好的检测结果，往往存在较差的抗干扰能力以及对方向性过于敏感等不足之处。基于小波变换边缘检测方法[3-4]具有良好的局域化特性，它是检测边缘很好的工具，但是该方法边缘信息难以保留完全。数学形态学[5]是一种非线性的滤波方法，应用数学形态学可以简化图像数据，保持他们基本的形状特征。形态学在检测图像边缘的连续性以及各个方向性方面都优于其他的传统方法[6-8]，由于单一的结构元素只能检测出与结构元素同方向的边缘信息，而对其它方向的边缘并不敏感。不过，由于传统的数学形态学检测算法忽略了边缘的方向性，只针对图像边缘的强度信息进行处理。这种处理方式具有一定的局限性，存在图像检测出的边缘相对较宽以及分辨率低的不良现象。而且，使用单一的形态学梯度算法来对边缘信息进行提取，虽然可以抑制噪声，但也会存在对部分形态学梯度幅值与噪声相近或低于噪声的低强度边缘造成损坏。

针对上述传统图像边缘检测算法的不足，文中提出了一种基于改进的数学形态边缘检测算法。实验仿真表明，该算法在检测图像边缘信息的完整性方面具有良好的效果，同时，能确保图像边缘的平滑性。

1 传统形态边缘检测算子

数学形态学是一门建立在严格数学集合论基础上的学科，它的基本思想是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的[11]。数学形态学在图像数据的简化方面具有优势，同时能够确保图像数据的形状特征不改变，并将不相关的结构进行清理。数学形态学可以进行相关的运算，其主要的运算规则有：膨胀、腐蚀、开启以及闭合。

腐蚀运算的主要作用是使物体沿着边界逐渐减小的过程，膨胀则是合并的过程，它们之间的关系是互为对偶运算。

数学运算定义[9]如下：

(1) 腐蚀运算：

FΘB(x,y)=min{F(x-s,y-t)-B(s,t)}

(1)

(2) 膨胀运算：

F⊕B(x,y)=max{F(x-s,y-t)+B(s,t)}

(2)

式中：F(x,y)表示的是灰度图像；B(s,t)表示的是结构元素。

闭运算主要用来对物体内部细小空洞进行填充，开运算的功能则是用来将细小的物体删除，并将边缘某些不必要的内容清除。相应的，闭运算和开运算也是互为对偶的运算。

数学公式定义如下：

(3) 开运算：

F∘B=(FΘB)⊕B

(3)

(4) 闭运算：

F·B=(F⊕B)ΘB

(4)

式中：Θ用来描述的是腐蚀运算；⊕用来描述的是膨胀运算。形状决定图像中的对象及其特征。针对时域空间形状的研究是数学形态学的主要方向，因此，在图像处理方面应用形态学是非常适合的。膨胀运算、腐蚀运算、开启运算以及闭合运算都是基于集合的运算。其中，结构元素用来调节图像特征变换的几何结构，扮演着至关重要的角色。

在膨胀运算、腐蚀运算、开启运算以及闭合运算的基础上，能够推演出灰度形态梯度边缘检测算子、灰度腐蚀边缘检测算子和灰度膨胀边缘检测算子三个常见算子。它们的数学定义如下：

灰度膨胀边缘检测算子

Cgd=(f⊕g)(x,y)-f(x,y)

(5)

灰度腐蚀边缘检测算子

Cge=f(x,y)-(fΘg)(x,y)

(6)

灰度形态梯度边缘检测算子

Cgsun=(f⊕g)(x,y)-(fΘg)(x,y)

(7)

通过分析，可以看出上面的三个算子都是属于非线性差分算子，其本质在某种程度上是对传统线性差分算子的推广应用。式(5)用来描述形态膨胀，这种算子处理得到的图像的边缘比较模糊、产生的边缘信号也比较弱。式(6)用来描述形态腐蚀，这种算子处理得到的图像边缘信号比较强，不过在噪声方面有所增强。文献(10)中修正了灰度形态学梯度边缘检测算子：

(8)

文献中对边缘检测算子进行数学定义：

E(x,y)=Ed(x,y)+0.5Edec(x,y)

(9)

通过上面的公式能够清晰地反映出文献(10)在检测结果的模糊性方面具有一定的优势，能够降低模糊性，是因为该算子对原图像的一些边缘细节信息进行了迭加。因为光源照射等原因，图像中具有更低的噪声梯度幅值以及形态学梯度幅值。因此，在图像处理中提取边缘时，如果只应用式(9)梯度阈值方法进行则往往容易对这类边缘造成损坏。

2 形态边缘检测算子的改进

2.1 算子原理

针对传统的形态边缘检测算子所存在的种种不足，文中提出了一种抗噪型检测算子，是对传统的检测算子的改进。

通过对形态学边缘检测算子的研究可以看出，如果出现噪声点的尺度小于检测算子的结构元尺度的情况，则在去除图像噪声方面形态边缘检测算子可以显现出明显的效果。虽然这种大尺度的结构元素具有很强的噪声去除能力，便于对原图像中对象的整体轮廓进行定位，不过，也存在一定的不足，往往会将原图像中某些细小的边缘信息当作噪声去处理。而如果出现检测算子的结构元尺度小于噪声点的尺度的情况，则存在对图像中的噪声难以消除的现象，虽然其在图像细节保持方面具有很好的效果。

针对上述存在的不足问题，文献中给出了多尺度多结构元边缘检测算子来解决该问题。其数学定义：

(10)

式中：EN(x,y)用来描述多尺度图像边缘检测结果；EM(x,y)用来描述多结构元图像边缘检测结果；ai用来描述加权系数。不过，因为计算复杂度高等因素的影响，该算子一直难以在实际的研究中推广应用。

鉴于此，本文在该算子的基础上进行了改进，即使用双结构不同尺度的两个结构元素来对图像进行交替顺序形态开闭滤波，对噪声采用平滑图像的方式去除处理，对单一结构元素处理所存在的问题进行了根本性的解决。

改进的双结构元素多尺度形态学边缘检测算子的数学定义：

E(F)=(F∘B)⊕A-(F·B)ΘA

(11)

式中，A的用钻石型5×5结构元素来描述，而B用十字型3×3结构元素来描述，它们都是基于不同尺度的结构素。

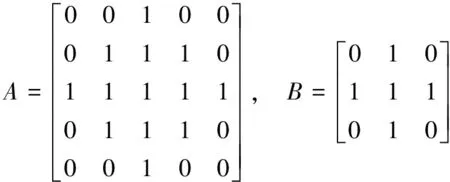
式中：A为小尺度的结构元素，它的优点是能够将图像的边缘信息很好的保持住，但它也存在不足之处，即对噪声去除处理欠缺；而B为大尺度的结构元素，它的优点是对噪声去除处理效果好，但也存在不足之处就是会将一些边缘信息去除。因此，在文中提出的改进算法中，充分的将A、B的优点保存下来，而将其不足去除，这样不但能有效地保持好边缘信息，而且对噪声的处理也非常有效果。

2.2 改进的边缘检测算法的描述

上面对改进的形态边缘检测算子的原理进行了说明。针对该改进的算法的执行流程用图1描述。

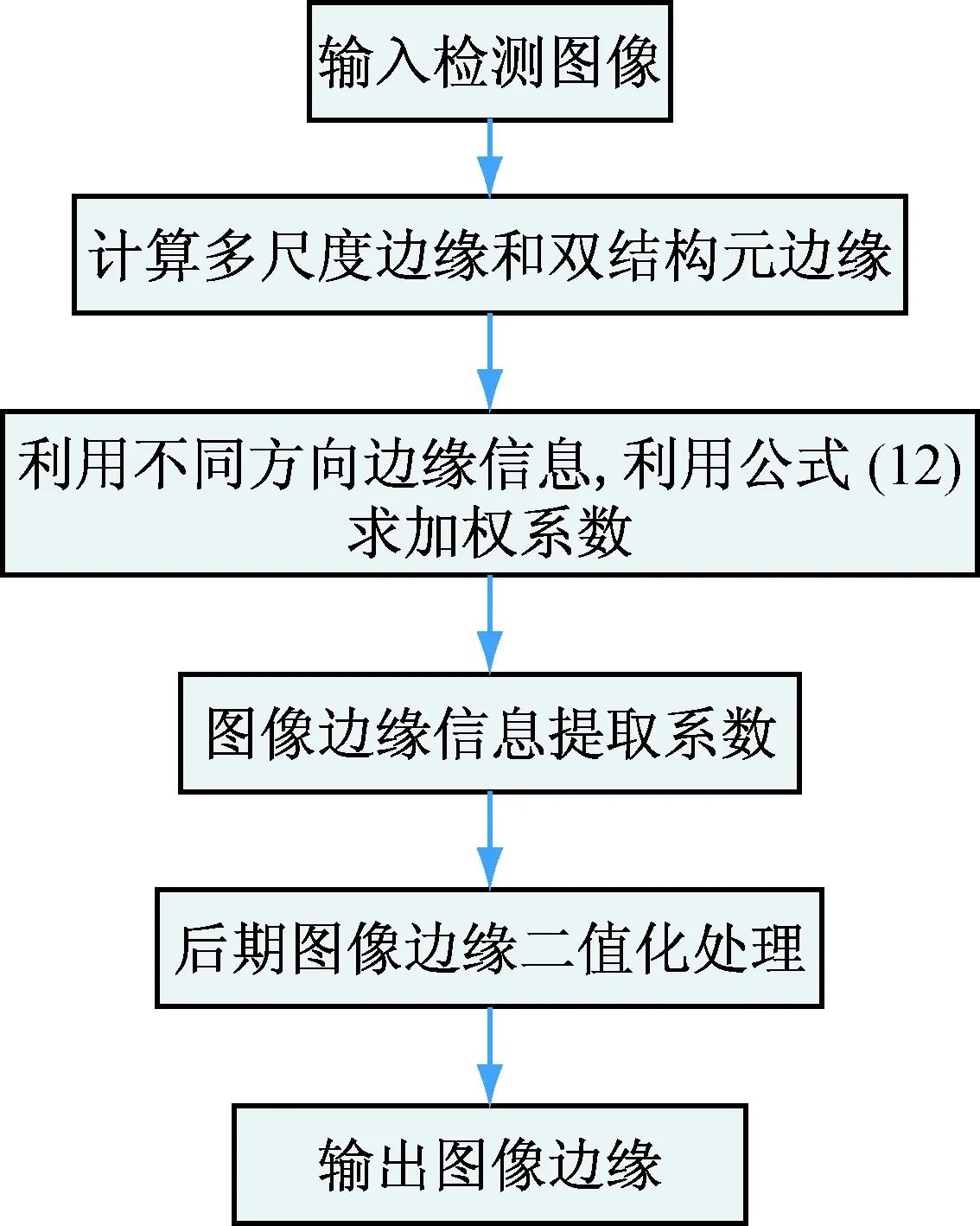
图1 算法流程图

本文改进的算法的执行步骤如下：

Step1：先将图像输入，然后利用形态开闭平滑对图像进行处理，目的是将图像中的噪声进行去除。

Step2：计算多尺度边缘结果以及双结构元素边缘。

Step3：在提取图像的边缘信息时采用不同方向的结构元素。然后将各个方向的边缘进行加权求和处理，最终就可以计算出图像的边缘信息。利用公式(12) 求得加权和结果：

(12)

式中，ai用来描述加权系数。

Step4：二值化处理得到的边缘信息，最后得到检测的边缘。

3 实验结果与分析

在Matlab7.0实验环境下，根据上面所提出的方法，进行图像边缘检测试验，本文算法简单、易于实现。给出了两个实验，① 将算法应用在灰度图像中，② 本文算法应用在彩色图像边缘检测中，其中两幅图像均为噪声图像。为了检测算法的有效性，本文给出了几种常见的边缘检测算法结果图，见图2及图3。在本文仿真实验中，选用两种结构元素类型为十字型结构3×3和钻石型5×5结构型。

从实验结果不难看出，在初始边缘检测结果(边缘图像)中，原始图像模糊的部分边缘像素的连续性较差。在更大尺度上检测到的边缘是对初始检测结果的有效补充。这种补充是建立在利用图像信息基础上的，并且因为尺度较大，在补充边缘信息的同时，有效地抑制了噪声的干扰。

(a) 噪声图像

(b) 小波方法

(c) 传统形态学检测

(d) 文献10检测

(e) 本文算法

(a) 噪声图像

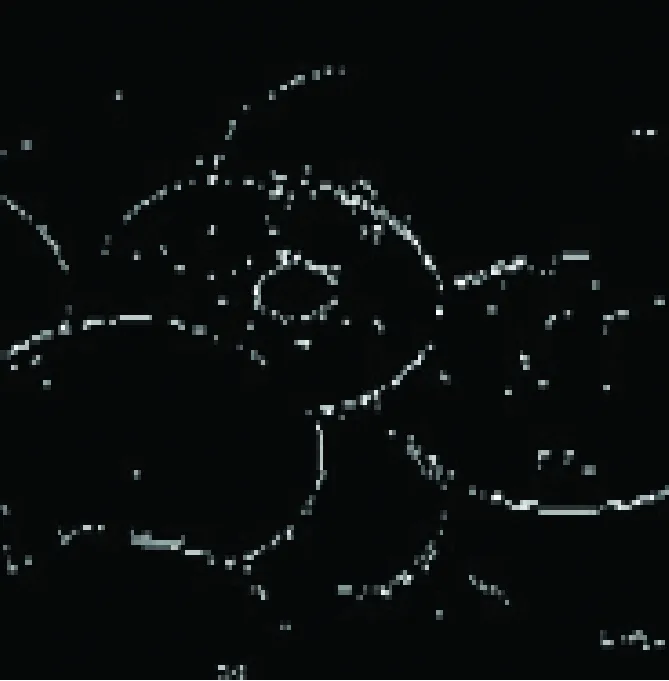
(b) 小波方法

(c) 传统形态学检测

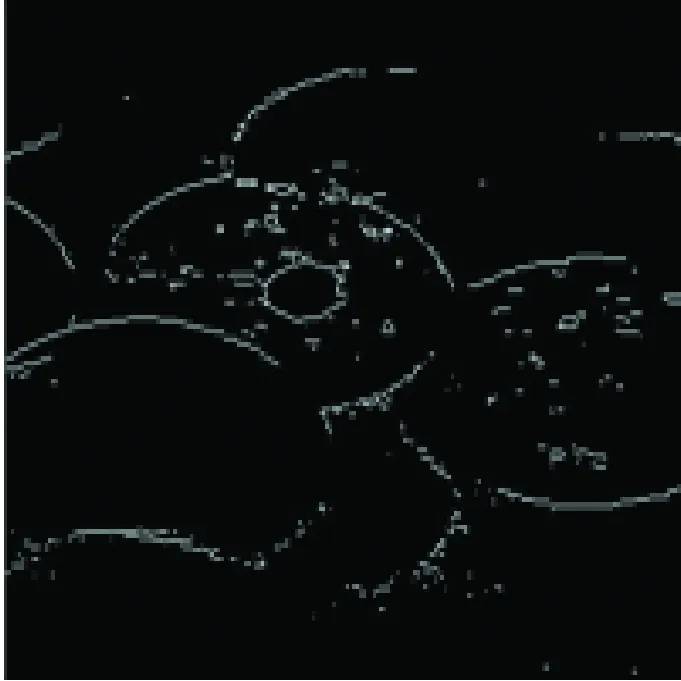
(d) 文献10检测

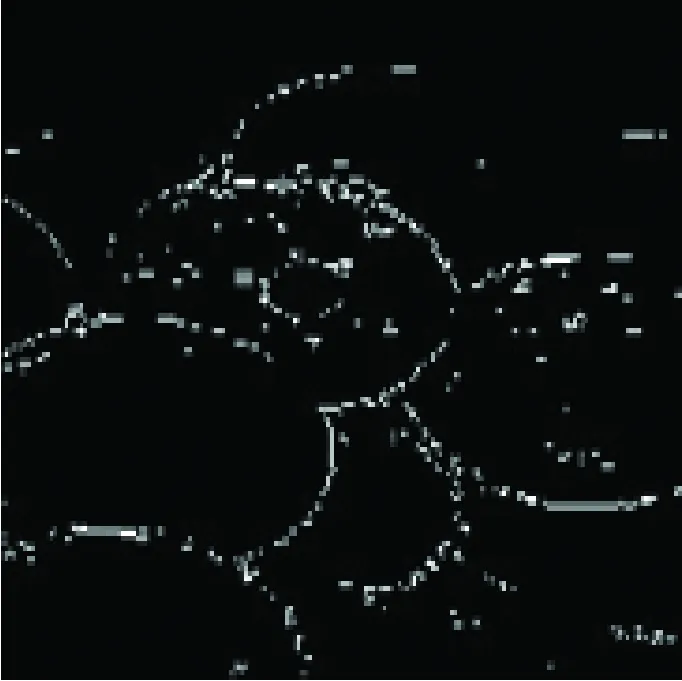
(e) 本文算法

4 结 语

针对传统边缘检测算法存在的边缘分辨率较低、低强度边缘保护能力较差等问题，提出了基于数学形态学彩色图像边缘检测改进算法。该方法将利用数学形态四种运算，膨胀、腐蚀、开、闭等变换以及它们的组合，并根据不同的结构元素的尺度大小和结构元类型，给出了一种改进的形态学抗噪型边缘检测算子，有效地检测出完整的图像边缘信息，并保持图像边缘的平滑性。实验结果证明了，与传统的边缘检测算法相比，本文提出的算法能有效提取准确的边缘信息，而且又具有很强的抗噪性，是一种有效的边缘检测方法。更加充分地利用了图像信息，提高了边缘检测的正确率。

[1] 孙江雄,谷达宝. 基于小波域多状态隐马尔科夫树模型多尺度文本图像分割[J]. 模式识别, 2004,37(7):1315-1324.

SUN J X,GU D B. A multiscale edge detection algorithm based on wavelet domain vector hidden Markov tree model[J].PatternRecognition,2004,37(7):1315-1324.

[2] 张 琳,薄 鹏. 小波域内基于尺度乘法的边缘检测[J].模式识别, 2002,23(14):1771-1784.

ZHANG L, BAO P. Edge detection by scale multiplication in wavelet domain[J]. Pattern Recognition Letters, 2002,23(14):1771-1784.

[3] 付永庆,王咏胜.一种基于数学形态学的灰度图像边缘检测算法[J].哈尔滨工程大学学报,2005,26(5):685-687.

FU Yong-qing,WANG Yong-sheng.An algorithm for edge detection of gray-scale image based on mathematical morphology[J]. Journal of Harbin Engineering University,2005,26(5):685-687.

[4] 杨 晖,张继武.数学形态学在图像边缘检测中的应用研究[J].辽宁大学学报,2005,32(1):50-53.

YANG Hui,ZHANG Ji-wu. Research on Application of Mathematical Morphology in Edge Detection of Image[J]. Journal of Liaoning University,2005,32(1):50-53.

[5] 刘 清，林士胜.基于数学形态学的图像边缘近侧算法[J].华南理工大学学报，2008，36(9):113-116.

LIU Qing,LIN Shi-sheng. Image Edge Processing based on Mathematical-morphology[J]. Journal of South China University of Technology，2008，36(9):113-116.

[6] 林世毅，苏广川，陈 东，等.基于小波变换和数学形态学的边缘检测法[J].仪器仪表学报，2004，25(4)：685-687.

LIN Shi-yi,SU Guang-chuan,CHEN Dong,etal. Edge Detection Based on Wavelet Transform and Morphology[J]. Journal of Scientific Instrument，2004，25(4)：685-687.

[7] 崔 屹.图像处理与分析——数学形态学方法及应用[M].背景：科学技术出版社，2000:56-201.

[8] Canny J E. A computional approach to edge detection[J].IEEE Trans on PAM 1,1985,8(6):679-698.

[9] 罗圣敏. 基于数学形态学的自适应边缘检测新算法[J]. 计算机仿真，2009，29(4):997-1000.

LUO Sheng-min. Adaptive algorithm of edge detection based on mathematical morphology[J]. Computer Simulation，2009,29(4):997-1000.

[10] 王万良,周 明,徐新黎.基于改进粒子群算法的离子膜车间调度问题研究[J].控制与决策,2010,25(7):1021-1025.

WANG Wan-liang,ZHOU Ming, XU Xin-li. Based on improved particle swarm caustic Shop Scheduling Problem[J]. Control and Decision,2010,25(7):1021-1025.

[11] 何怡刚,祝文姬,周炎涛.基于粒子群算法的模拟电路故障诊断方法[J].电工技术学报,2010,25(6):163-171.

HE Yi-gang,ZHU Wen-ji,ZHOU Yan-tao. Analog circuit fault diagnosis method based on particle swarm optimization algorithm[J]. Journal of Electrician Technique,2010,25(6):163-171.

[12] 邹 恩,陈建国,李祥飞.一种改进的变尺度混沌优化方法及其仿真研究[J].系统仿真学报,2006,18(9):2426-2430.

ZOU En, CHEN Jian-guo, LI Xiang-fei. Research on an improved mutative scale chaos optimization method and its simulation[J]. Journal of system simulation,2006,18(9):2426-2430.

[13] 滕 皓,邵阔义,曹爱增,等. 量子遗传算法的变尺度混沌优化策略研究[J]. 计算机应用研究,2009,26(2):543-546.

TENG Hao, SHAO Kuo-yi, CAO Ai-zeng,etal.Study on mutative scale chaos optimization strategy of quantum genetic algorithm[J]. The research and application of computer,2009,26(2):543-546.

[14] 滕 皓,曹爱增,杨炳儒.一种改进变尺度混沌优化的模糊量子遗传算法[J].计算机工程,2010,36(7):175-177.

TENG Hao, CAO Ai-zeng, YANG Bing-ru. An improved mutative scale chaos optimization fuzzy quantum genetic algorithm[J]. Computer Engineering,2010,36(7):175-177.

[15] 闫海霞，赵晓晖. 基于书序形态学的边缘检测方法[J]. 计算机应用研究，2008,25(11):3497-3499.

YAN Hai-xia, ZHAO Xiao-hui. Detection method of book order morphology based edge[J]. The research and application of computer，2008,25(11):3497-3499.