多块体形状堆石体碾压颗粒破碎数值模拟

刘 洋 ，李晓柱，吴顺川

（1.北京科技大学 土木系，北京 100083；2.北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083；3.中冶集团武汉勘察研究院有限公司，武汉 430080）

1 引 言

随着我国基础建设的发展，堆石、砂砾、粗粒土等散体材料被广泛应用于水利、港口、交通等岩土工程建设中，散粒体材料无论在运输、施工碾压、稳定承载等过程中都存在着颗粒破碎现象，颗粒破碎将引起材料粒径、级配和密度发生变化，进而影响其物理力学性质。

颗粒破碎的早期研究主要是针对砂颗粒破碎（如Terzaghi 等[1]、DeBeer 等[2]）。同时期的研究者Kjaernsli 等[3]和Hall 等[4]则进一步考虑了颗粒形状、粗糙度和级配对破碎的影响。颗粒破碎问题已逐渐引起人们的重视，目前的研究主要集中在以下几方面：（1）颗粒破碎程度的量化描述；（2）影响颗粒破碎的因素；（3）颗粒破碎对散粒体力学性质特别是强度、剪胀特性等的影响；（4）考虑颗粒破碎的散粒体应力-应变关系建立。

颗粒破碎的定量描述是研究颗粒破碎的基础，不同学者根据试验和理论分析提出了不同的量化表述方法，有的学者采用界限粒径（如Lee 等[5]、Lade等[6]），或各粒组破碎前后含量（如Marsal 等[7]）的变化来描述颗粒破碎程度；有的学者采用破碎后的新增表面积来表示颗粒的破碎程度（如Miura等[8]）。Hardin[9]引入了破碎势的概念，提出了一种新的表示破碎的方法，还定义了相对破碎Br的概念，研究了中间粒径对颗粒破碎的影响，Br计算方便而应用较广泛。孔德志等[10]、孙吉主等[11]也对这个问题进行了研究。此外，分形理论也被引入用于描述颗粒破碎后的粒径分布问题（如McDowell 等[12]、Coop等[13]、张季如等[14]、Einav 等[15-16]），Einav 等还根据分形分析结果对Hardin 破碎指标进行了修正。

影响颗粒破碎的因素很多诸如颗粒本身的矿物硬度、颗粒形状、级配等内在因素以及应力水平、应力路径、加载方式、湿化程度等外在因素。国内外不少学者对这些影响因素做了较多的试验研究和理论分析（如梁军等[17]、Indraranta 等[18-19]、陈生水等[20]）。

颗粒破碎引起的粒径、级配、密度的变化不可避免地会影响散粒体的强度与变形。Miura 等[8]研究认为颗粒破碎会使散粒体峰值内摩擦角减小，剪胀趋势降低。Ueng 等[21]建立了考虑颗粒破碎的应力-应变关系，并结合Rowe 剪胀方程讨论了颗粒破碎引起的强度变化。

基于上述颗粒破碎对材料剪胀性和峰值强度的影响，国内外学者在经典弹塑性理论和边界面塑性理论等框架下开展了考虑颗粒破碎的本构模型方面的研究（如Daouadji 等[22]、迟世春等[23]、Yao 等[24]、孙海忠等[25]、刘恩龙等[26-27]）。

对颗粒破碎研究另一个值得注意的方向是微细观力学分析与数值模拟，Potapov 等[28]对颗粒碰撞破碎的机制和破碎过程进行了数值模拟，提出了二维应力条件下单颗粒破碎的2 阶段概念。数值模拟方面采用最多的是离散单元法，不少学者采用这种方法研究了颗粒破碎对散粒体力学行为的影响（如Cheng 等[29-30]、Lobo-Guerrero[31]等）。离散单元法还被应用于堆石体[32-33]、级配碎石[34]、宕砟路堤[35]等岩土工程应用方面的研究。

对于具有超大粒径及高粒径差的堆石体，室内试验的局限性是显而易见的，无法从堆石体的大小、形状及级配组成等方面研究堆石体真实的工作状况和物理力学特性。基于此，本文考虑堆石散粒体的实际形状，通过6 种典型堆石块体形状近似，采用平行连接和接触连接两种接触模型，建立了多块体形状堆石体离散元数值模型，研究了堆石体在碾压荷载作用下的颗粒破碎机制及过程，探讨了颗粒破碎对堆石体碾压前、后级配曲线的影响，并进一步分析了颗粒形状对颗粒破碎的影响。

2 不同形状堆石块形成与破碎

2.1 基本和复杂颗粒形状

刘东等[36]在研究颗粒形状对堆石体力学特性影响时认为，由于堆石体的超大粒径及形状，其强度主要取决于堆石体之间的摩擦力和咬合力，而圆球颗粒无法模拟。刘君等[32]在采用单一类型颗粒簇进行堆石体颗粒破碎的离散元模拟时指出，单一颗粒形状的模拟结果与实际存在一定的偏差，采用多种组合形式可能会改善这种状况。

本文通过对现场堆石体堆积情况分析，选取了分布比较普遍的6 种代表性块体形状，采用离散元软件PFC2D进行建模分析，6 种形状见图1。

图1 堆石块体形状简化示意图Fig.1 Representative shape sketches of rock fill

2.2 颗粒簇模型

利用颗粒簇建立上述6 种块体形状，分别为类圆锯齿形、类梯形、类椭圆形、类三角形和类长方形等，6 种形状的颗粒簇及组成情况见表1。表中，n0为每种颗粒簇所含的连接个数；a为颗粒簇的方位角；rm为组成颗粒簇小颗粒的半径；为在初始纯圆颗粒上生成颗粒簇的额外孔隙（阴影部分），相关计算和参数推导见章节2.3。

表1 代表性块体形状及几何参数Table 1 Six representative shapes of rock fill and geometric parameters

2.3 颗粒簇块体与初始纯圆颗粒转换

初始纯圆颗粒转换为颗粒簇块体时应遵循质量等效原则，即

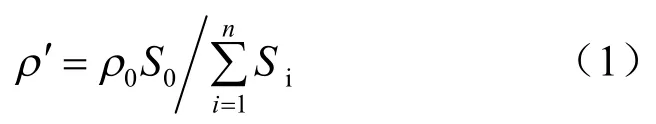
式中：ρ0为初始纯圆颗粒密度；S0为初始纯圆颗粒面积；Si为构成颗粒簇小颗粒面积；ρ′为构成颗粒簇的小颗粒密度，不同形状的块体其对应的各颗粒簇等效密度见表1。

在数值模拟中初始孔隙率对模拟结果影响较大，为了较好地控制初始孔隙率，表1 给出了初始纯圆颗粒转换为颗粒簇颗粒引起的额外孔隙。以类圆锯齿状颗粒为例，见图2(a)。

图2 颗粒破碎前后孔隙变化Fig.2 Variation of void before and after crushing

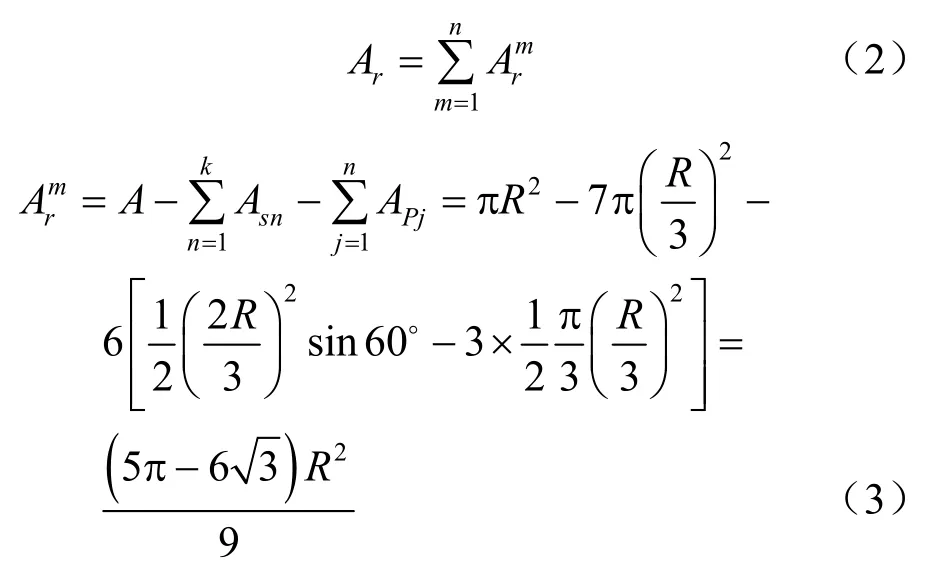
式中：A为初始纯圆颗粒面积；Ar为初始纯圆颗粒生成颗粒簇额外增加的总孔隙；Asn为组成颗粒簇的每个小颗粒面积；APj为生成颗粒簇产生的内部孔隙。

颗粒破碎前后孔隙变化见图2(b)，需要指出的是，破碎前内部孔隙设其归属为密实块体，不属于孔隙范畴，破碎后其变为增加的额外孔隙。

2.4 颗粒破碎

碾压荷载下颗粒破碎如图3 所示。图中，实线是现存的接触连接和平行连接位置；虚线表示该处颗粒黏结已破坏；黑色粗实线表示由于颗粒破碎引起的颗粒之间的裂隙。

若小颗粒周围连接或黏结全部破坏，该颗粒从簇上分离为单颗粒，在后续的计算中服从接触刚度模型。小颗粒分离后不再发生2 次破碎，而剩余的块体形状比基本的6 种形状更复杂，仍可能发生进一步的破碎，因此，数值模拟虽然采用6 种基本形状，但计算过程中颗粒形状远不止这6 种。

图3 颗粒破碎示意图Fig.3 Sketches of particle crushing

破裂率定义为：b=n/N，n为连接破裂总数；N 模型中初始连接总数。

另外，定义切向破裂率bs=ns/n，法向破裂率bn=nn/n，ns为连接切向破裂个数；nn为法向破裂个数，用于分析破裂中切向破裂和法向破裂所占比重。

3 多块体形状堆石体碾压数值模型

碾压模型取自现场碾压试验[33]，采用上面提出的6 种块体形状单元建立多形状堆石体碾压模型。数值模型采用离散元软件PFC2D建立，异形颗粒簇单元是利用Fish 语言编程实现，过程可见文献[33]。

3.1 接触本构模型

为了较好地模拟颗粒破碎特性，分别采用接触连接和平行连接两种接触本构模型对堆石体现场碾压试验进行数值模拟和破碎分析，并比较这两种接触本构对模拟结果的影响。

3.2 堆石体模型建立

数值模拟采用与实际大型现场碾压试验相仿的尺寸，模型尺寸为6 m×2 m，选取摊铺厚度为105 cm和120 cm。模型边界由左、右和下部3 道墙体形成，底层铺设50 cm 的级配碎石褥垫层，预先碾压平衡后铺设堆石体。

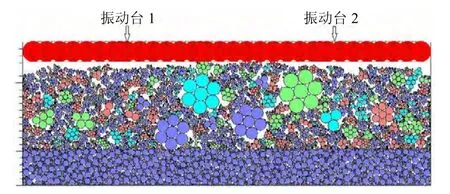
图4 多块体形状堆石体振动碾压数值模型Fig.4 Rolling compaction numerical model for rockfill of different particle shapes

数值模型建立步骤：首先，建立纯圆形颗粒模型，颗粒级配按现场堆石级配确定。然后，利用Fish函数记录纯圆颗粒的坐标和粒径。删去纯圆颗粒，在原来位置随机生成与纯圆颗粒等价的不同形状的颗粒簇。最后，施加重力并达到初始平衡状态（见图4）。模型中类圆锯齿形C1有985 个、类梯形C2有238 个、类椭圆形C3有535 个、类三角形C4有820 个、类长方形C51有194 个、C52有228 个，模型细观参数见表2。

表2 模型细观参数Table 2 Micro-parameters of numerical model

需要指出的是，细观参数的选取对离散元的模拟结果影响很大，本文的做法是根据现场堆石体及室内试验获取的堆石体的地质强度指标（GSI），单轴抗压强度（UCS）等宏观参数，根据Hoek-Brown强度准则得到不同围压条件下岩块的峰值强度曲线。然后根据经验给定一组细观参数，通过不同围压的双轴压缩数值试验，获得一组围压与峰值强度的关系，与通过宏观参数确定的HB 强度包络线进行比较，若一致，则选取该组细观参数，不一致，则继续重复上面步骤，以获得相应的细观参数，限于篇幅，这里不再详述。

3.3 振动碾压荷载施加

现场采用SANY-YZ26E 型振动碾，按搭接20 cm 全振碾压。数值模型中通过将直径为0.3 m 的圆盘颗粒叠合构成clump 块来模拟实际振动碾压，为了更好地模拟交错碾压荷载对颗粒破碎的影响，数值模型每遍的碾压荷载分别通过振动台1和振动台2 来施加。

振动碾压采用弹跳模型的运动方程为

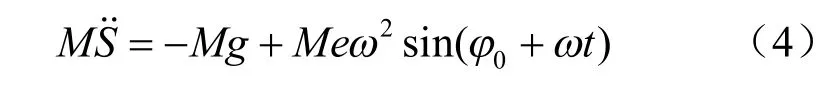
式中：M为系统质量；e为振动偏心距；S为位移；g为重力加速度；ω为振动圆频率；φ0为起跳临界角；t为振动持时。

任意时间振动碾速度为

式中：V(t)为振动碾压速度；π为圆周率。

运用能量等价法为

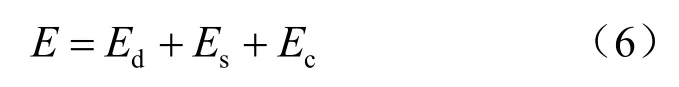
式中：E为总能量；Ed为动能；Es为势能；Ec为冲击能。由此可以得出振动碾压每遍碾压试验所采用的细观参数。

4 数值模拟结果分析

4.1 一般结果

平行连接模型中摊铺厚度为120 cm，接触连接模型中为105 cm。图5、6 分别为2 个模型碾压8遍过程中堆石体的颗粒破碎分布及受力性状。

图5(a)和6(a)为初始堆积状态。由6 种不同形状的颗粒簇形成的堆石体，颗粒簇总数3 000 个，初始连接总数19 237 个。图5(b)、6(b)为堆石体自重应力平衡状态。在自重应力作用下颗粒不断向下移动，堆石体颗粒重新分布，细颗粒开始填充到粗颗粒孔隙中，模型产生压缩、孔隙比减小。随着颗粒相互接触形成，粒间接触力发展，图中线条粗细表示颗粒间接触力的大小，自重平衡后底部颗粒间相互作用力较大。

自重平衡后施加8 遍碾压荷载，图5(c)～5(j)、6(c)～6(j)为每遍碾压后的堆石颗粒破碎位置分布图。为清楚起见，图中仅显示了发生破裂的颗粒。以平行连接模型为例，图5(c)为碾压1 遍后颗粒破碎的分布情况，其中切向破裂个数5 个，法向破裂个数为717 个，破裂总数为722 个，总破碎率为3.75%，其中切向破裂率为0.78%，法向破裂率为99.22%。

4.2 颗粒破碎率与碾压遍数的关系

图7为颗粒破碎率与碾压遍数的关系。从图中可以看出，随着碾压遍数的增加，颗粒破碎率逐渐增大，颗粒破碎主要发生在碾压荷载施加的前4 遍，碾压4 遍后颗粒破碎率增加缓慢。这是因为初始阶段堆石块体松散地堆积在褥垫层上，随着碾压荷载的施加，颗粒开始向下运动，小颗粒向孔隙中充填，但其运动过程中由于大颗粒的阻挡，颗粒之间开始出现摩擦、滑移和破碎。随着碾压荷载的进一步施加，颗粒之间的孔隙逐渐减小，颗粒之间棱角度变小，颗粒的摩擦、滑移及破碎缓慢地消耗内部累积的弹性能并逐渐稳定。

4.3 振动碾压荷载下的颗粒破碎特性

由图7(b)可以看出，与静荷载下堆石体的颗粒破碎不同，碾压荷载作用下堆石体颗粒破碎以法向破裂为主，表明在振动碾压荷载下颗粒破碎以张拉破坏为主；无论是平行连接模型还是接触连接模型，碾压前4 遍切向破裂率均在10%以内且增长缓慢，法向破裂率虽逐渐减小但均在90%以上，说明碾压前4 遍堆石体在振动碾压荷载下以张拉破坏为主。从图5、6 中也可以看出，当法向接触应力大于初始法向连接力后法向连接破裂并出现张拉破坏。

碾压4 遍后切向破裂率有所增加，达到近20%，并最终趋于平稳，法向破裂率继续减小最终趋于稳定。随着碾压荷载的施加，堆石体颗粒渐趋于密实，虽然继续施加振动碾压荷载，但此时堆石体颗粒与颗粒之间相互接触，具有一定的承载能力，局部开始出现明显的剪切破坏，如图5(f)、图6(g) 所示。红色粗实线为剪切破裂发展趋势线，颗粒破碎沿着近似倾斜45°左右方向朝底部延伸，从而使切向破裂率缓慢增加，但仍以张拉破坏为主。

4.4 颗粒破碎对堆石体级配曲线的影响

堆石料的颗粒破碎使原有的级配发生变化，发生颗粒破碎时，大颗粒会破碎，小颗粒也会破碎，同时前一级大颗粒破碎时新生成不同粒径的小颗粒又会继续破碎，这样连环式的破碎造成了土体颗粒级配的改变，但如何来量化级配变化是一个值得研究的问题。

现场碾压试验的级配变化是通过现场取样进行室内筛分来确定，但对于数值模拟中颗粒级配变化情况的定量研究较少。本节通过现场堆石体碾压试验及6 种不同形状的颗粒破碎数值模拟，提出以下方法来表示颗粒破碎引起的堆石体级配变化情况。

假设初始颗粒簇为一密实的块体（即图2 中的内部孔隙忽略不计），初始面积为计算公式见表1），生成颗粒簇的初始圆半径为 Rm，按照每个颗粒簇的最终破裂个数 ni来计算其破碎率 bm，按照破碎率计算破裂后颗粒的等效粒径 dm，且破裂后仍等效为圆形的颗粒。如果ni≤n0j按照面积等效来计算其破裂后颗粒粒径dm；如果ni=n0j，则假定颗粒簇完全破碎分解为所组成的细颗粒。

图5 平行连接颗粒破碎模型颗粒破碎及受力性状Fig.5 Force distribution and particle crushing for parallel-bounded model

图6 接触连接颗粒破碎模型颗粒破碎及受力性状Fig.6 Force distribution and particle crushing for contact-bounded model

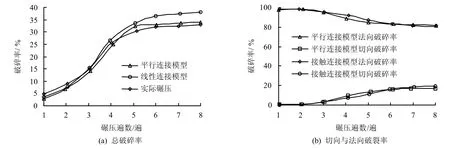
图7 颗粒破碎率与碾压遍数的关系Fig.7 Relationships of crushing ration and numbers of rolling compaction

在数值试验中通过编制Fish函数来统计每个颗粒簇（本文模型中共3 000 个）的破碎情况，绘制碾压破碎后的颗粒级配图，并与现场碾压试验进行对比分析，具体计算如下：

图8为堆石体碾压前、后级配曲线变化图。由图可以看出，由于颗粒破碎堆石体粒径组成发生了明显变化。数值模拟的级配曲线与现场碾压试验后的级配曲线变化趋势相同，说明采用的数值试验和分析方法在一定程度上可以模拟振动碾压堆石体颗粒破碎。由图中还可以看出，数值模拟在大粒径（100 mm≤d ≤800 mm）区域的粒径变化幅度比现场试验大，这主要是由于建立的数值模型颗粒簇与实际堆石体的差异所致。

图8 堆石体碾压前后级配变化图Fig.8 Variation of gradation curves for rockfill

图9为类圆锯齿形颗粒簇破碎前、后示意图，颗粒簇初始赋予12个相等的连接力将7个小颗粒连接在一起形成一个类块体，但实际堆石体为致密块体，特别是粒径越大，模型中生成的这种颗粒簇的差异就越大。假设实际堆石体初始粒径为800 mm，在数值模拟中施加的振动碾压荷载使颗粒簇之间很容易产生应力集中，局部轻微的应力集中就会使图9 中的7 个连接力破坏。实际模拟中可能会更明显，如图5(f)～5(g)及6(g)～6(h)所示，大粒径颗粒簇连接力基本完全破坏、颗粒破碎明显。

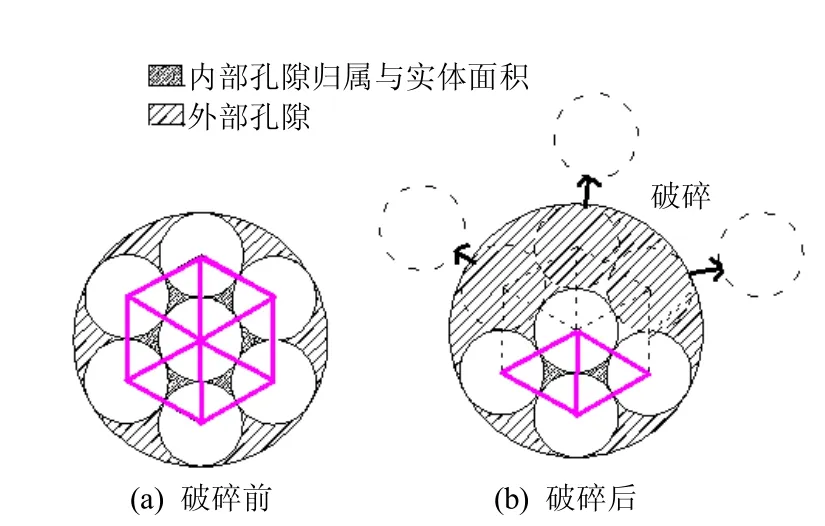
图9 颗粒簇颗粒破碎前、后变化情况示意图Fig.9 Sketch of particle cluster before and after crushing

4.5 接触本构对模拟结果的影响

（1）对接触力的影响

由图5、6 堆石体颗粒间受力性状可以看出，平行连接模型的粒间接触力（数量级109N）明显大于接触连接模型（数量级106N）。赋于颗粒相同的连接力，平行连接模型颗粒之间的刚度明显大于接触连接模型。从图5 还可以看出，平行连接模型碾压前5 遍粒间接触力总体呈缓慢增大趋势，碾压第2遍时粒间接触力最大，碾压第6、7 遍时粒间接触力缓慢减小，但碾压第8 遍粒间接触力又轻微增大。这是因为在施加振动荷载初期，颗粒之间会出现滑移挤压甚至局部嵌合，堆石体颗粒的棱角之间会出现明显的应力集中，导致了在碾压第2 遍时粒间接触力达到了最大值。

随着碾压荷载的施加，颗粒开始逐渐破碎，棱角缓慢磨圆，颗粒之间开始紧密接触，荷载传递趋于均匀，颗粒间接触力缓慢增加。当大颗粒之间孔隙被细小颗粒填充，此时无论是大颗粒还是小颗粒，位置基本不变，颗粒与颗粒紧密接触，逐步消散碾压荷载所施加的弹性能，颗粒间接触力开始减小。当继续施加碾压荷载时，此时碾压荷载不足以使稳定的颗粒继续破碎，颗粒之间的弹性能来不及消散，所以接触应力也出现了轻微的增加。

对于接触连接模型，碾压前7 遍粒间接触力整体呈增大趋势，碾压第5 遍粒间接触力突然减小，之后继续增加，碾压第8 遍颗粒间接触力又开始减小，最大接触力出现在碾压的第7 遍。这是因为接触连接模型相对平行连接模型来说，呈现类似柔性的特性。碾压荷载施加起始，接触连接模型这种种柔性使得颗粒簇颗粒之间的荷载可以均匀传递，颗粒之间接触力缓慢增加，整个碾压过程没出现明显的回弹。碾压第5 遍时粒间接触力的突然减小是因为碾压第5 遍颗粒破碎数量急剧增加（见图6(g)），颗粒破碎消耗了大量的弹性能，因此，外在表现出颗粒间的接触力突然减小。

（2）对颗粒破碎率模拟结果的影响

由图7 可以看出，碾压前3 遍现场试验的颗粒破碎大于数值模拟结果，碾压后5 遍接触连接模型颗粒破碎明显，但数值模拟结果和实际试验基本一致。平行连接模型颗粒破碎率与实际试验结果吻合较好，显然该模型更接近于实际堆石体的力学响应。

（3）对级配曲线模拟结果的影响

由图8 可以看出，接触与平行连接模型碾压后级配曲线在大粒径区域几乎一致，在小粒径区域（d≤100 mm）接触连接模型碾压后级配曲线高于平行连接模型和实际试验结果，这说明接触连接模型在小粒径区域破碎明显，这是因为接触连接相对于实际堆石体刚度偏小，而平行连接模型碾压后级配曲线与现场碾压后级配曲线几乎重合，可见平行连接模型对现场碾压试验级配曲线变化的模拟结果较好。

图9 中，3 个细颗粒在7 个连接力破坏后分散，余下块体的等效粒径为611 mm。但实际堆石体碾压试验中碾压后取样分析表明，由于块体的致密性，大部分大粒径堆石体碾压仅是棱角的磨圆过程（除了少数内部结构面发育明显的块体），因此，在大粒径区域数值模拟破碎率较实际试验偏高。

另一方面，由于模型生成颗粒簇的细颗粒数目有限，这在一定程度上会减小这种差异（见表1），即使完全破裂后颗粒的粒径也仅为 Rn/3，之后细颗粒将不再继续破碎。

5 颗粒形状对破碎影响的进一步讨论

纯圆形颗粒存在过度旋转的问题，在实际堆石体现场，由于爆破形成的堆石体其形状各异，纯圆形颗粒及单一的非圆颗粒不能反映实际堆石体的物理力学特性，但对于多种复杂形状的块体其计算效率会比较低。下面通过上述6 种颗粒簇形状系数的分析，进一步探讨块体形状对堆石体破碎的影响。

首先建立单一形状堆石体数值模型（6 种颗粒形状），其局部视图见图10。采用孔亮等[37]对颗粒形状的描述方法，颗粒的形状系数用颗粒的圆形度与凸凹度的加权平均来表示，即

式中：F1为圆形度，定义为

式中：As为与块体同周长的圆面积；Af为块体实际面积；F2为凸凹度，定义为

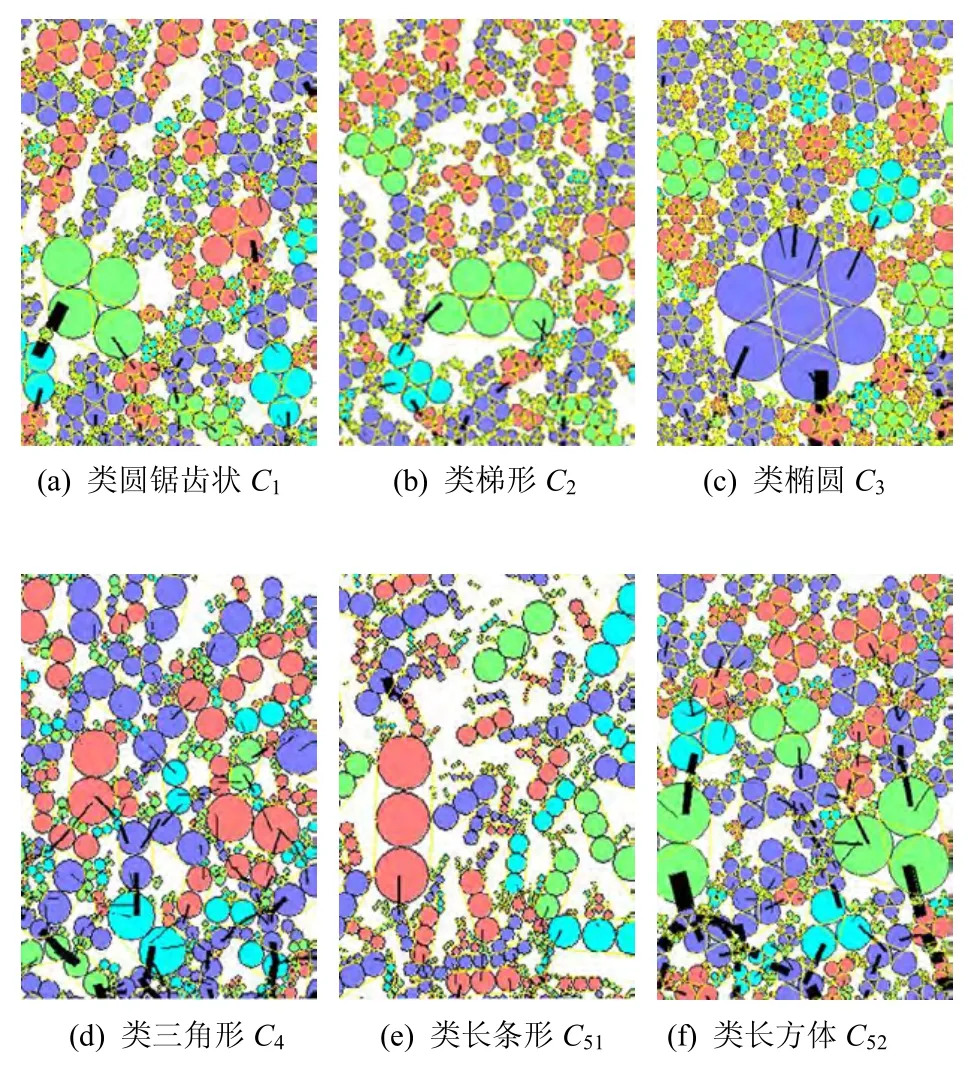
图10 6 种不同形状颗粒数值试验模型Fig.10 One-shape numerical model of different shapes

采用这种方法得到6 种不同形状（类圆锯齿形C1、类梯形C2、类椭圆形C3、类三角形C4、类长方形C51、C52）的颗粒形状系数及碾压后颗粒破碎率，见表3。

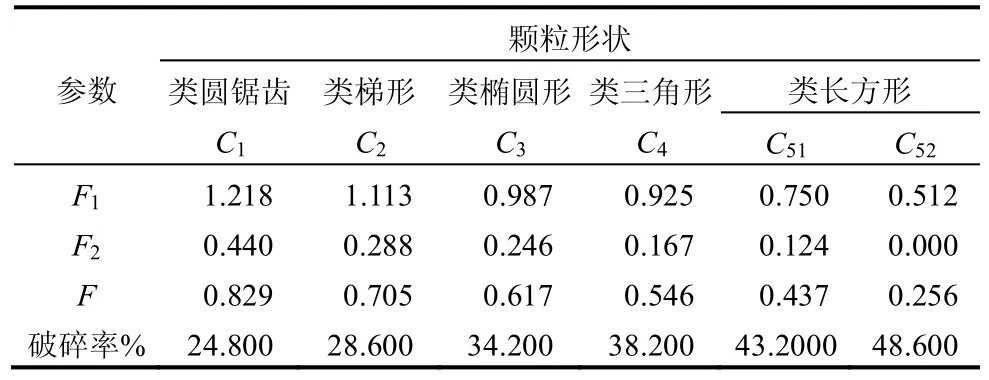
表3 颗粒的形状系数及碾压后颗粒破碎率Table 3 Shape coefficient and crushing ration of particle

由表3 中可以看出，随着形状系数的增加，颗粒破碎率逐渐降低，说明颗粒破碎率与颗粒形状系数密切相关，其中类长方形颗粒在碾压荷载作用下颗粒破碎明显，且具有明显的水平倾向性，而其他形状颗粒没有明显的水平倾向性。类椭圆形颗粒破碎率与实际试验颗粒破碎率基本一致，显然对于特大堆石体模型，为了简化颗粒模型，提高计算效率，可以考虑采用单一椭圆形颗粒。

总体来说，颗粒形状对散粒体的宏观力学性质影响较大，相对于纯圆形颗粒，异形颗粒可以近似模拟颗粒间的咬合作用，更接近堆石体的实际工作状态，当然关于颗粒形状对颗粒破碎的影响尚需进一步开展研究工作。

6 结 论

（1）相比较于纯圆颗粒或单一非圆颗粒，采用的6 种颗粒形状建立的堆石体振动碾压离散元模型，可以较好地模拟堆石体的物理力学性质，更接近于堆石体的实际工作状态。

（2）在碾压荷载作用下堆石颗粒破碎以张拉破坏为主，随着碾压遍数的增加，局部开始出现剪切破碎。接触连接模型的破碎率要高于现场试验结果，而平行连接模型对堆石体的碾压试验模拟较好。

（3）建立的颗粒破碎量化计算方法，虽然在大粒径范围粒径变化幅度比现场试验偏大，但整体趋势仍比较吻合，可以用于分析碾压前、后堆石体级配曲线的变化。

（4）随着块体形状系数的增加，颗粒破碎率逐渐降低，其中类长方形颗粒在碾压荷载作用下颗粒破碎明显，且具有明显的水平倾向性。类椭圆形块体破碎率与实际试验的结果基本一致，对于特大堆石体数值模拟，可以考虑采用单一椭圆形块体模型，提高计算效率。

需要指出的是，本文进行的是二维颗粒破碎模拟，虽然在孔隙比计算上采用了二维、三维孔隙转化，但实际的颗粒破碎为三维问题，更复杂。因此进一步的工作应建立三维颗粒破碎模型，并着重开展颗粒破碎机制和破碎模式的研究。

[1]TERZAGHI K,PECK R B.Soil mechanics in engineering practice[M].New York:Wiley,1948.

[2]DEBEER E E.The scale effect in the transposition of the results of deep sounding tests on the ultimate bearing capacity of piles and caisson foundations[J].Geotechnique,1963,13(1):39-75.

[3]KJAERNSLI B,SANDE A.Compressibility of some coarse-grained materials[C]//Proc.European Conf.Soil Mech.&Found.Engrg.Weisbaden,German:[s.n.],1963:245-251.

[4]HALL E B,GORDON B B.Triaxial testing with large-scale high pressure equipment[R].ASTP Philadephia:Laboratory shear testing of soils,ASTM STP 361,1963:315-328.

[5]LEE K L,FARHOOMAND.Compressibility and crushing of granular soils in anisotropic triaxial compression[J].Can.Geotech.,1967,4(1):68-86.

[6]LADE P V,YAMAMURO J.Significance of particle crushing in granular materials[J].Journal of Geotechnical Engineering,1996,122(4):309-316.

[7]MARSAL R J.Large scale testing of rockfill materials[J].Journal of the Soil Mechanics and Foundations Division,1967,93(SM2):27-43.

[8]MIURA N,O HARA S.Particle crushing of a decomposed granite soil under shear stresses[J].Soils and Foundations,1979,19(3):61-76.

[9]HARDIN B O.Crushing of soil particles[J].Journal of Geotechnical Engineering,1985,111(10):1177-1192.

[10]孔德志,张其光,张丙印,等.人工堆石料的颗粒破碎率[J].清华大学学报(自然科学版),2009,49(6):811-815.KONG De-zhi,ZHANG Qi-guang,ZHANG Bing-yin,et al.Particle breakage ratio of artificial rockfill materials[J].Journal of Tsinghua University(Science &Technology),2009,49(6):811-815.

[11]孙吉主,汪稔.三轴压缩条件下钙质砂的颗粒破裂过程研究[J].岩土力学,2003,24(5):822-825.SUN Ji-zhu,WANG Ren.Study on particle failure process of calcareous sand under triaxial compression[J].Rock and Soil Mechanics,2003,24(5):822-825.

[12]MCDOWELL G R,BOLTON M D,ROBERTSON D.The fractal crushing of granular materials[J].J.Mech.Phys.Solids,1996,44(12):2079-2102.

[13]COOP M R,SORENSEN K K,FREITAS T B,et al.Particle breakage during shearing of carbonate sand[J].Geotechnique,2004,54(3):157-163.

[14]张季如,祝杰,黄文竞.侧限压缩下石英砂砾的颗粒破碎特性及其分形描述[J].岩土工程学报,2008,30(6) :783-789.ZHANG Ji-ru,ZHU Jie,HUANG Wen-jing.Crushing and fractal behaviors of quartz sand-gravel particles under confined compression[J].Chinese Journal of Geotechnical Engineering,2008,30(6):783-789.

[15]EINAV I.Breakage mechanics——part I:Theory[J].Journal of the Mechanics and Physics of Solids,2007,55(6):1274-1297.

[16]EINAV I.Soil mechanics:Breaking ground[J].Plilos Transactions,Series A,Mathematical,Physical,and Engineering Sciences,2007,365:2985-3002.

[17]梁军,刘汉龙,高玉峰.堆石蠕变机制分析与颗粒破碎特性研究[J].岩土力学,2003,24(3):479-483.LIANG Jun,LIU Han-long,GAO Yu-feng.Creep mechanism and breakage behaviour of rockfill[J].Rock and Soil Mechanics,2003,24(3):479-483.

[18]INDRARATNA B,LACKENBY J,CHRISTIE D.Effect of confining pressure on the degradation of ballast under cyclic loading[J].Geotechnique,2005,55(4):325-328.

[19]LACKENBY J,INDRARATNA B,MCDOWELL G,et al.Effect of confining pressure on ballast degradation and deformation under cyclic triaxial loading[J].Geotechnique,2007,57(6):527-536.

[20]陈生水,韩华强,傅华.循环荷载下堆石料应力变形特性研究[J].岩土工程学报,2010,32(8):1151-1157.CHEN Sheng-shui,HAN Hua-qiang,FU Hua.Stress and deformation behaviors of rockfill under cyclic loadings[J].Chinese Journal of Geotechnical Engineering,2010,32(8):1151-1157.

[21]UENG T S,CHEN T J.Energy aspects of particle breakage in drained shear of sands[J].Geotechnique,2000,50(1) :65-72.

[22]DAOUADJI A,HICHER P Y,RAHMA A.An elastoplastic model for granular materials taking into account grain breakage[J].European Journal of Mechanics(A/Solids),2001,20(1):113-137.

[23]迟世春,贾宇峰.土颗粒破碎耗能对罗维剪胀模型的修正[J].岩土工程学报,2005,27(11):1255-1269.CHI Shi-chun,JIA Yu-feng.Rowe’s stress-dilatancy model modified for energy dissipation of particle breakage[J].Chinese Journal of Geotechnical Engineering,2005,27(I1):1263-669.

[24]YAO Y P,YAMAMOTOH,WANG N D.Constitutive model considering sand crushing[J].Soils and Foundations,2008,48(4):603-608.

[25]孙海忠,黄茂松.考虑颗粒破碎的粗粒土临界状态弹塑性本构模型[J].岩土工程学报,2010,32(8):1284-1290.SUN Hai-zhong,HUANG Mao-song.Critical state elastoplastic model for coarse granular aggregates incorporating particle breakage[J].Chinese Journal of Geotechnical Engineering,2010,32(8):1284-1290.

[26]刘恩龙,陈生水,李国英,等.堆石料的临界状态与考虑颗粒破碎的本构模型[J].岩土力学,2011,32(增刊2):148-154.LIU En-long,CHEN Sheng-shui,LI Guo-ying,et al.Critical state of rockfill materials and a constitutive model considering grain crushing[J].Rock and Soil Mechanics,2011,32(Supp.2):148-154.

[27]刘恩龙,陈生水,李国英,等.循环荷载作用下考虑颗粒破碎的堆石体本构模型[J].岩土力学,2012,33(7):57-63.LIU En-long,CHEN Sheng-shui,LI Guo-ying,et al.A constitutive model for rockfill materials incorporating grain crushing under cyclic loading[J].Rock and Soil Mechanics,2012,33(7):57-63.

[28]POTAPOV A V,CAMPBELL C S.Parametric dependence of particle breakage mechanisms[J].Powder Technology,2001,120(3):164-174.

[29]CHENG Y P,NAKATA Y,BOLTON M D.Discrete element simulation of crushable soil[J].Geotechnique,2003,53(7):633-641.

[30]CHENG Y P,BOLTON M D and NAKATA Y.Crushing and plastic deformation of soils simulated using DEM[J].Geotechnique,2004,54(2):131-141.

[31] LOBO-GUERRERO S,VALLEJO L E.Discrete element method evaluation of granular crushing under direct shear test conditions[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131(10):1295-1300.

[32]刘君,刘福海,孔宪京.考虑破碎的堆石体颗粒流数值模拟[J].岩石力学与工程学报,2008,29(11):107-112.LIU Jun,LIU Fu-hai,KONG Xian-jing,Particle flow code numerical simulation of particle breakage of rockfill[J].Rock and Soil Mechanics,2008,29(11),107-112.

[33]李晓柱,刘洋,吴顺川.堆石坝现场碾压试验与离散元数值分析[J].岩石力学与工程学报,2013,待刊 .LI Xiao-zhu,LIU Yang,WU Shun-chuan.Experiemntal investigation and discrete element numerical analysis of roller compaction test in site for rockfill dam[J].Chinese Journal of Rock Mechanics and Engineering,2013,in press.

[34]蒋应军,任皎龙,徐寅善,等.级配碎石力学性能的颗粒流数值模拟方法[J].同济大学学报(自然科学版),2011,39(5):699-704.JIANG Ying-jun,REN Jiao-long,XU Yin-shan,et al.Simulation method of mechanical properties of graded broken stone based on particle flow code[J].Journal of Tongji University(Natural Science),2011,39(5):699-704.

[35]周忠,秦长国,徐永福,等.宕渣路堤碾压过程的数值模拟[J].中外公路,2008,28(6):45-49.ZHOU Zhong,QIN Chang-guo,XU Yong-fu,et al.The numerical simulation of down slag embankment compaction process[J].Journal of China &Foreign Highway,2008,28(6):45-49.

[36]刘东,谢婷蜓,马刚,等.颗粒形状对堆石体真三轴数值试验力学特性的影响[J].水电能源科学,2011,29(9):68-71.LIU Dong,XIE Ting-ting,MA Gang,et al.Numerical simulation of true triaxial test for behavior of rockf ill based on grain shape[J].Water Resources and Power,2011,29(9):68-71.

[37]孔亮,彭仁.颗粒形状对类砂土力学性质影响的颗粒流模拟[J].岩石力学与工程学报,2011,30(11):2113-2119.KONG Liang,PENG Ren.Particle flow simulation of influence of particle shape on mechanical properties of quasi-sands[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(11):2113-2119.