粗粒土剪胀性大型三轴试验研究

姜景山 ，程展林，左永振，丁红顺

（1.南京工程学院 建筑工程学院，南京 211167；2.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010）

1 引 言

土体的剪胀性是指在剪应力作用下土体体积产生的变化，体积增大称为剪胀，体积减小称为剪缩，土体的剪胀、剪缩性，统称为剪胀性。剪胀性作为土体的基本特性之一，显著区别于一般的弹性材料，其特点在于：（1）土体的剪胀性非常明显，剪应力引起的体积变化可能与压应力引起的体积变化在数量上属于同一量级，往往不可忽略；（2）土中可能出现负的剪胀（体积以压缩为正，即剪缩为正，剪胀为负），即剪缩，土体体积减小，也会出现正的剪胀，或负的剪缩，土体体积增大[1]。

一般认为，土的剪胀性是正的即土体体积是增大的，并解释土体剪胀性的原因，可能与在试验中没有将体变明确划分为压应力引起的压缩性体变和剪应力引起的剪胀性体变有关。Henkel[2]和Parry[3]通过平均压应力不变的饱和黏土的三轴剪切试验表明，即使没有压应力的影响土中也会出现负的剪胀变形，即在单纯剪应力作用下土体体积也可能压缩，体积减小。

众多学者已经通过试验研究、数值模拟和理论分析等对土体的剪胀性开展了较多的研究[2-14]，并分析了颗粒形状、大小和级配等因素对土体剪胀性的影响[7,10-11]，取得了丰硕的研究成果，为土力学的发展做出了重要的贡献。但上述研究大都从总体变的角度出发对土体的剪胀性进行研究，研究的土体也主要集中在黏土和砂土等，较少从总体变分解成压应力引起的体变和剪应力引起的体变角度出发研究土的剪胀性。

粗粒土是由大小不同、形状不一、性质各异的土颗粒相互填充而成的散体状颗粒集合体，具有强度高、变形小、渗透性好、就地取材等优点在土石坝填筑工程中广泛应用。由于粗粒土的粒径相对较大，剪胀性产生的机制、特性以及对强度和变形的影响等与砂土和黏性土等或多或少地存在一定差异，同时现有的研究成果大多是从总体变的角度出发研究土的剪胀性，因而有必要在常用的大型三轴试验的基础上从总体变分解成压应力引起的体变和剪应力引起的体变的角度出发对粗粒土的剪胀性进行研究。

2 试 验

粗粒土三轴试验是在长江科学院水利部岩土力学与工程重点实验室的应力应变式大型高压三轴仪上进行，试样尺寸（直径×高度）为30 cm×60 cm，试验为饱和固结排水三轴剪切试验，剪切速率为0.6 mm/min。共进行了4 组不同初始密度的常规三轴试验，初始干密度 ρd分别为2.05、2.10、2.17、2.27 g/cm3。每组试验3 个点，试验围压σ3为0.4、0.8、1.6 MPa。

试验材料为金沙江塔城水电站良美砂砾石，颗粒较浑圆、扁平。母岩质地坚硬，颗粒强度高，试验材料和试验级配曲线分别见图1、2。

图1 塔城砂砾石Fig.1 Tacheng sand gravel

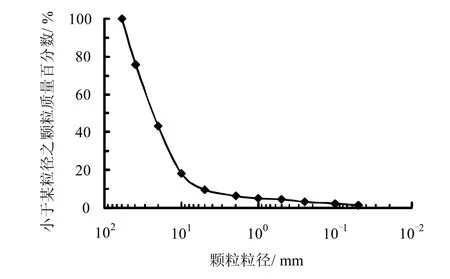
图2 试验级配曲线Fig.2 Particle size distribution curve

3 应力-应变关系

图3为不同初始密度的塔城砂砾石应力-应变关系曲线（轴向应变 εa和体变 εv均以压缩为正）。从图中可以看出，低围压下（σ3=0.4 MPa）应力-应变曲线呈软化型，体胀变形较大；初始干密度越大，应力-应变曲线越陡峭，软化特征越明显，峰值强度越高，但围压一定时所有密度的试样在高应变（εa=15%）时偏应力σ1-σ3（σ1为轴向应力）逐渐趋于一致，即强度基本相同。从图3 还可以看出，在三轴固结排水剪切过程中体变有两种形式，一种是体胀型或剪胀型，剪切初期先呈体缩变形，然后产生较大的体胀变形，如图3（1）所示。体缩和体胀的拐点斜率为0（dεv/dεa=0，图中向下箭头所指示的点），拐点之前体变斜率为正，拐点之后曲线斜率为负，斜率最小（dεv/dεa=min，图中向上箭头所指示的点）的点出现在体胀段；另一种是体缩型或剪缩型，如图3（3）所示。剪切过程中体变总是压缩的，体变曲线斜率最小的点出现在体缩的末端，为便于论述，假定此点为硬化型曲线的剪胀点（dεv/dεa=0）和软化点（dεv/dεa=min）。

对于软化型曲线，当体变由体缩变为体胀时（拐点），表明剪应力引起的体胀已经与压应力引起的体缩相当，此时强度增长变得越来越缓慢，至剪胀效应最大时，强度（峰值强度）达到最大。此后，随着轴向应变的增大，强度又有所减小，并逐渐趋向于某一残余强度，与试验开始时的土体的松密程度无关而只与围压有关[15]。

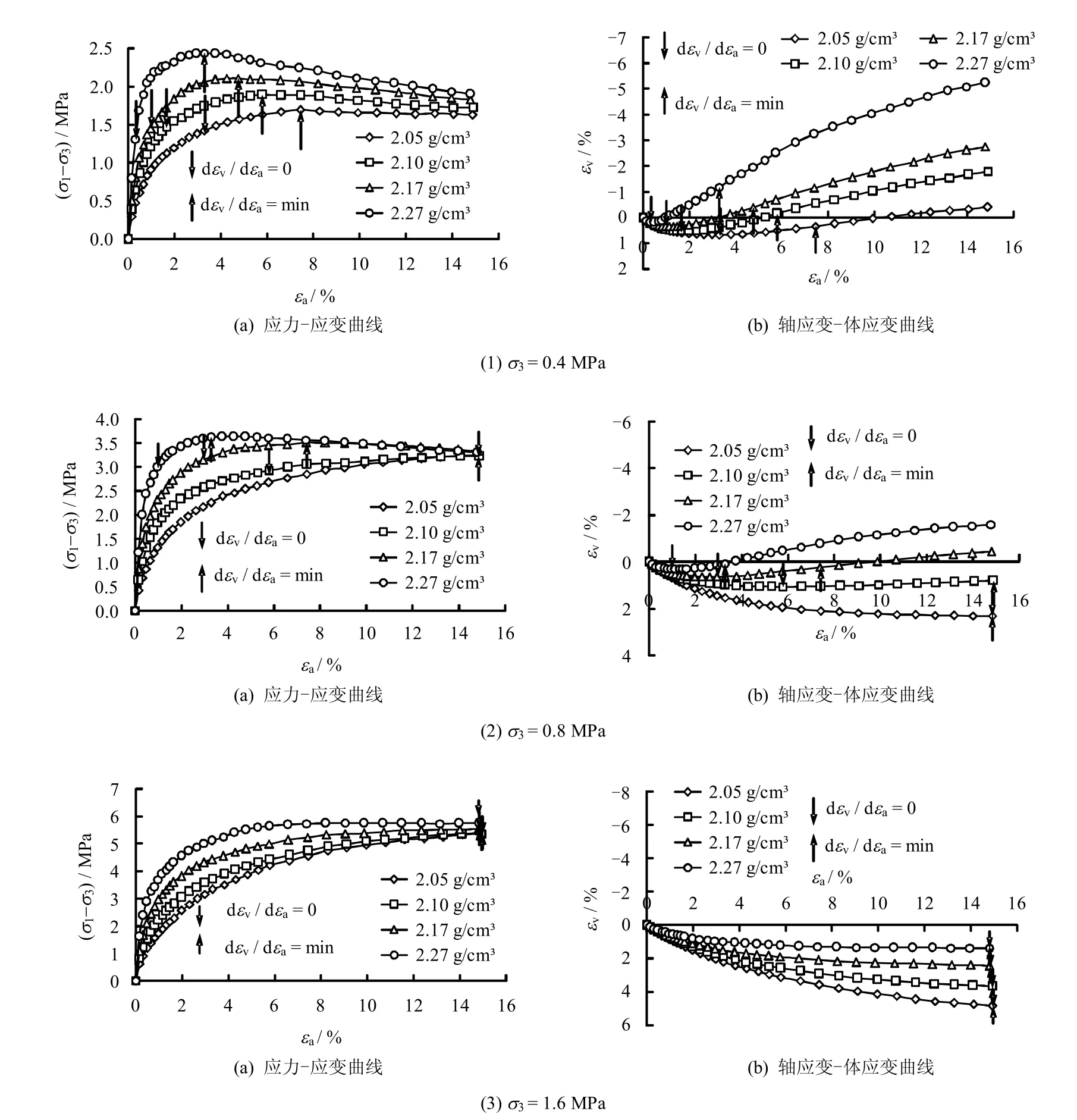
图3 不同初始密度试验的应力应变曲线Fig.3 Stress-strain curves of tests at different initial densities

图4为不同初始密度的塔城砂砾石发生剪胀（dεv/dεa=0）和软化（dεv/dεa=min）时的轴向应变。从图中可以看出，低围压下剪胀和软化时的轴向应变都较小，并且随着试样初始干密度的增大而减小，同一试验中软化时的轴向应变要大于剪胀时的轴向应变。随着围压的增大，剪胀和软化时相应的轴向应变增大，到较高围压时，不论初始干密度如何，由于应力-应变曲线呈硬化型，剪胀和软化时的轴向应变均为15%。

图5为不同初始密度的塔城砂砾石发生剪胀（dεv/dεa=0）和软化（dεv/dεa=min）时的体变。从图中可以看出，低围压下剪胀和软化时的体变较小且随着试样初始干密度的增大而减小，同时剪胀时的体变不小于软化时的体变。随着围压的增大，剪胀和软化时的体变也逐渐增大，但在高围压下，剪胀和软化时的体变相等。图6为不同初始密度的塔城砂砾石发生剪胀（dεv/dεa=0）和软化（dεv/dεa=min）时的偏应力。由图可见，围压越小，剪胀和软化时的偏应力越小。低围压下（软化型曲线），剪胀时偏应力要小于软化时偏应力，其中剪胀时偏应力随初始干密度的增大变化不大，而软化时偏应力则随着初始干密度的增大而增大。高围压下剪胀和软化时的偏应力均随着初始干密度的增大而增大。

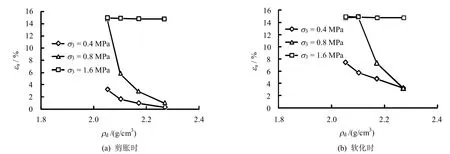
图4 剪胀和软化时的轴向应变Fig.4 Axial strain at dilatancy and softening

图5 剪胀和软化时的体变Fig.5 Volumetric strain at dilatancy and softening

图6 剪胀和软化时的偏应力Fig.6 Deviatoric stress at dilatancy and softening

4 体变速率

图7为塔城不同密度砂砾石的体变增量与轴向应变增量之比（dεv/dεa为体变速率）随轴向应变 εa的变化曲线。从图中可以看出，体变增量与轴向应变增量之比均随着轴向应变的增大从某一正值逐渐减小，说明一开始体变是压缩的且压缩量逐渐减小。某一初始密度的试样在不同围压下开始剪切时初始的体变增量与轴向应变增量之比比较接近，但随后表现出较大的变化差异。低围压下，体变增量与轴向应变增量之比减小得较快，并很快从正值变化到负值，说明体变是先压缩后膨胀的。较高围压下体变增量与轴向应变增量之比减小得相对于低围压下要缓慢一些，虽逐渐趋向于0 但都大于0，说明较高围压下体变基本都是压缩，随着剪切的进行体变逐渐增大并逐渐趋于平缓。

从图7 还可以看出，低围压下体变增量与轴向应变增量之比从正值减小到负值之后，继续减小达到最小值，随后又有所增大，但体变增量与轴向应变增量仍小于0，其最小值点基本对应于软化型应力-应变曲线的峰值强度点。较高围压下体变增量与轴向应变增量之比是单调减小的并大于0，应力-应变曲线表现为硬化型，无明显的峰值强度。另外，图中曲线有极少数点产生了相对较大的波动性和离散性，这可能与试验误差及粗粒土试验的不确定性有关[16]，但整体而言曲线的变化趋势十分清晰。

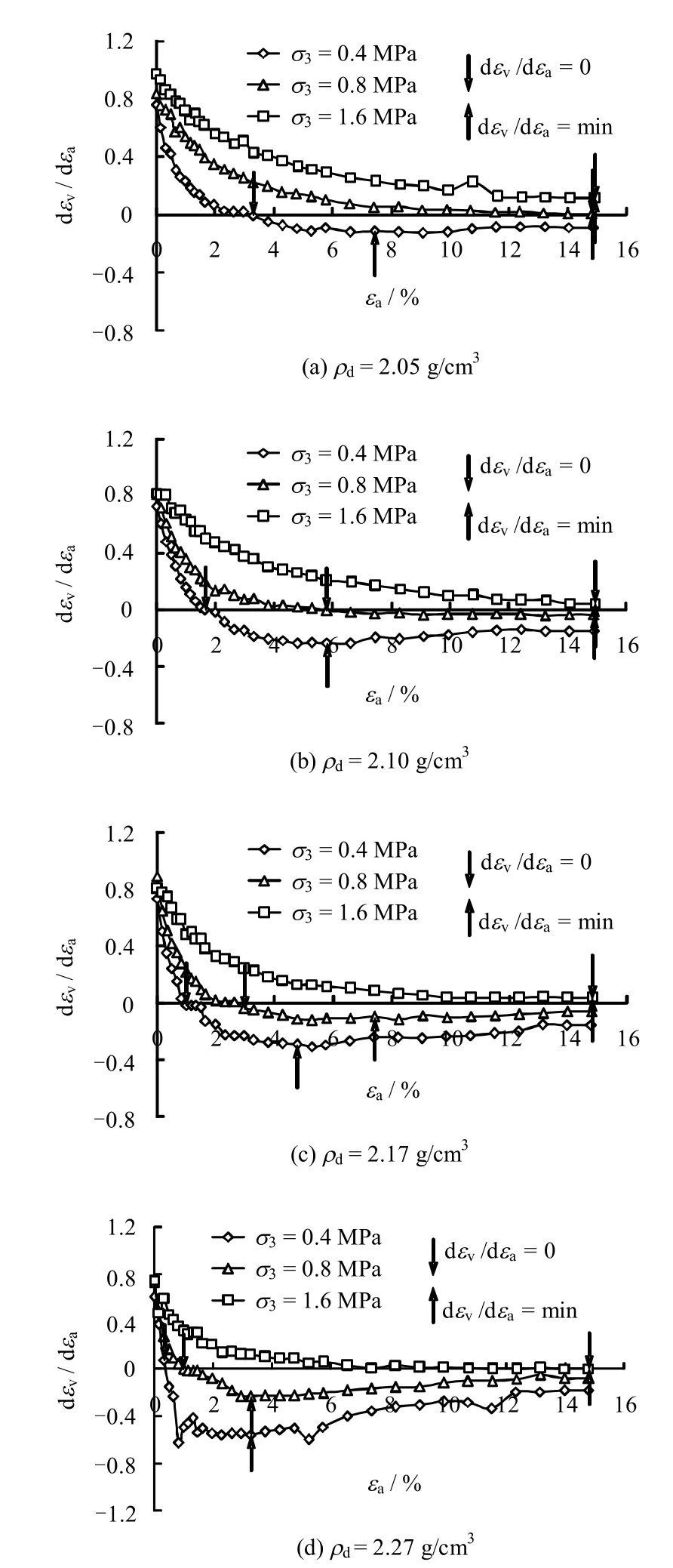
图7 体变增量-轴向应变增量之比Fig.7 Ratio of volumetric strain increment to axial strain increment

图8为体变速率与切线弹性模量 Et散点关系图（体变速率为（dεv/dεa），Et为d(σ1-σ3)/dεa）。从图中可以看出，体变速率基本随着切线弹性模量的增大而增大且增大趋势逐渐变缓，同种粗粒土在不同围压下体变速率比较接近。随着初始干密度的增大，体变速率略有减小且离散型稍有增大，可能与高密度、低围压下软化型曲线在峰值附近曲线形态变化较大有关。

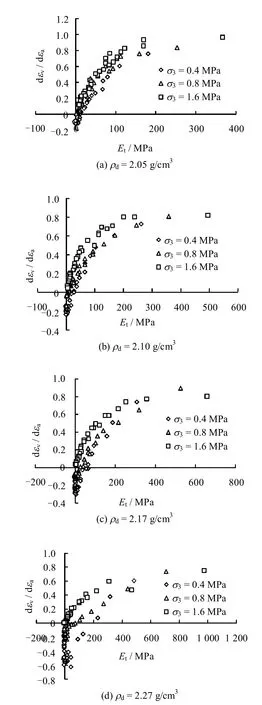
图8 体变速率-切线弹性模量的关系Fig.8 Relationship between volumetric strain ratio and tangent elastic modulus

5 非线性剪胀方程

粗粒土作为大小不同、形状不一、性质各异的土颗粒形成的颗粒集合体，其力学性质主要体现在颗粒本身的性质（颗粒大小、形状、级配、母岩性质等）和颗粒间相互作用上。程展林等[17]通过长期的粗粒土试验研究发现，Rowe 剪胀方程[18]能较好地反映颗粒状粗粒土的变形机制，特别是土的剪胀性，仅用一个Rowe 剪胀方程参数 Kf（Kf为颗粒单元滑动变形的最小能比，即外力对颗粒单元做功与颗粒单元对外做功之比的最小值）就能反映粗粒土的体变特征。

若将三轴试验条件下土体的体变分解为球应力（压应力）p 引起的体变和偏应力（剪应力）q 引起的体变，忽略球应力p 对偏应变 εs的直接影响[17]，则有下列方程：

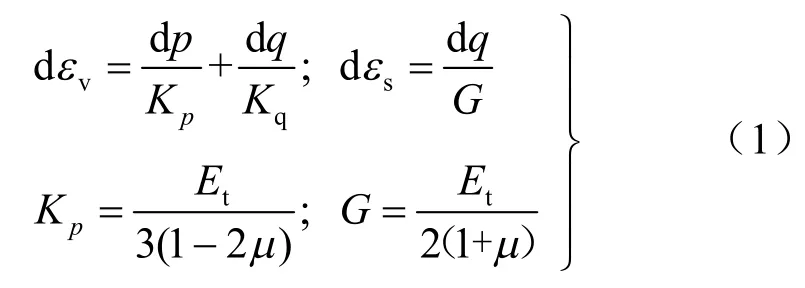
式中：Kp、Kq、G、Et、μ 分别为体变模量、剪胀模量、剪切模量、切线弹性模量（由邓肯-张模型计算求得）、泊松比。

针对三轴试验的体变，分离剪应力引起的体变为

常规三轴压缩试验条件下Rowe 剪胀方程为

故，式（3）变为

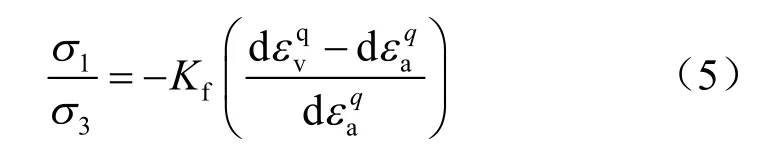
假定三轴试验的轴向应变增量dεa和剪应力引起的体变增量服从Rowe 剪胀方程，则由式（5）有

即为建立的非线性剪胀模型，它实际上是一个弹性非线性模型，详细的模型的建立、推导和验证参阅文献[17]，但本文仍就模型的实现过程做了适度的介绍，以便于和后面论述的内容保持较好的连贯性。从文献[17]中还可以看出，对于一般的粗粒土材料，Rowe 剪胀模型参数Kf＞1，本文塔城砂砾石的Rowe 剪胀模型参数 Kf也说明了这一点。

三轴试验条件下轴向应变为

则由式（6）可推导出剪胀模量为

可见剪应力引起的体变是压缩还是膨胀，取决于剪胀模量的正负，初始剪切阶段。当σ1＜Kfσ3时，剪胀模量Kq为正，剪应力引起的体变是压缩的；当σ1＞Kfσ3时，剪胀模量Kq为负，剪应力引起的体变是膨胀的。

图9为Rowe 剪胀方程计算得到的体变曲线。由图可以看出，计算的体变曲线与实测的体变曲线吻合良好，说明Rowe 剪胀方程能够较好地反映粗粒土的剪胀特性，能够用于粗粒土体变的计算。图10为根据式（6）整理的塔城砂砾石三轴试验的剪胀模型参数 Kf。由图可见，不同围压下剪胀参数 Kf的归一性非常好，不随着试验围压和轴向应变而变化，为一大于1 的常数，反映了粗粒土颗粒的性质及相互作用，是粗粒土组构特性的一种反映。

表1为塔城砂砾石的非线性剪胀模型的参数，除Rowe 剪胀参数Kf外，其他参数的含义及计算均同邓肯-张模型，并且仅用一个Rowe 剪胀方程参数Kf来描述粗粒土的体变特征，参数数量要少于邓肯-张模型，因而非线性剪胀模型是一种能较好地反映粗粒土剪胀性的较简单、实用的应力-应变关系模型。

图11为不同密度的塔城砂砾石Rowe 剪胀方程参数 Kf的平均值，可以看出，三轴试验条件下同一种粗粒土Rowe 剪胀模型参数 Kf基本不变，保持为一常数，其平均值为3.65，说明 Kf不仅与应力状态无关，也与初始密度无关，说明Rowe 剪胀方程参数Kf能较好地反映粗粒土的颗粒排列和相互作用，是粗粒土颗粒母岩性质、颗粒级配及受力过程中颗粒相互作用的综合体现。实际上也有其他学者从不同模型或角度研究和验证了Rowe 剪胀方程反映粗粒土体变的适用性和合理性[19-23]。

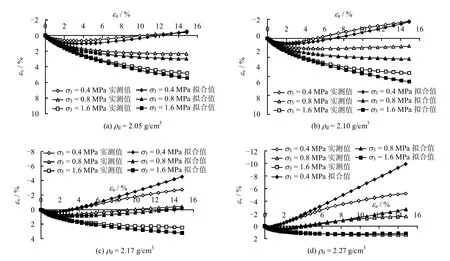
图9 Rowe 剪胀方程体变计算曲线Fig.9 Calculated curves of volumetric strain of Rowe dilatancy equation

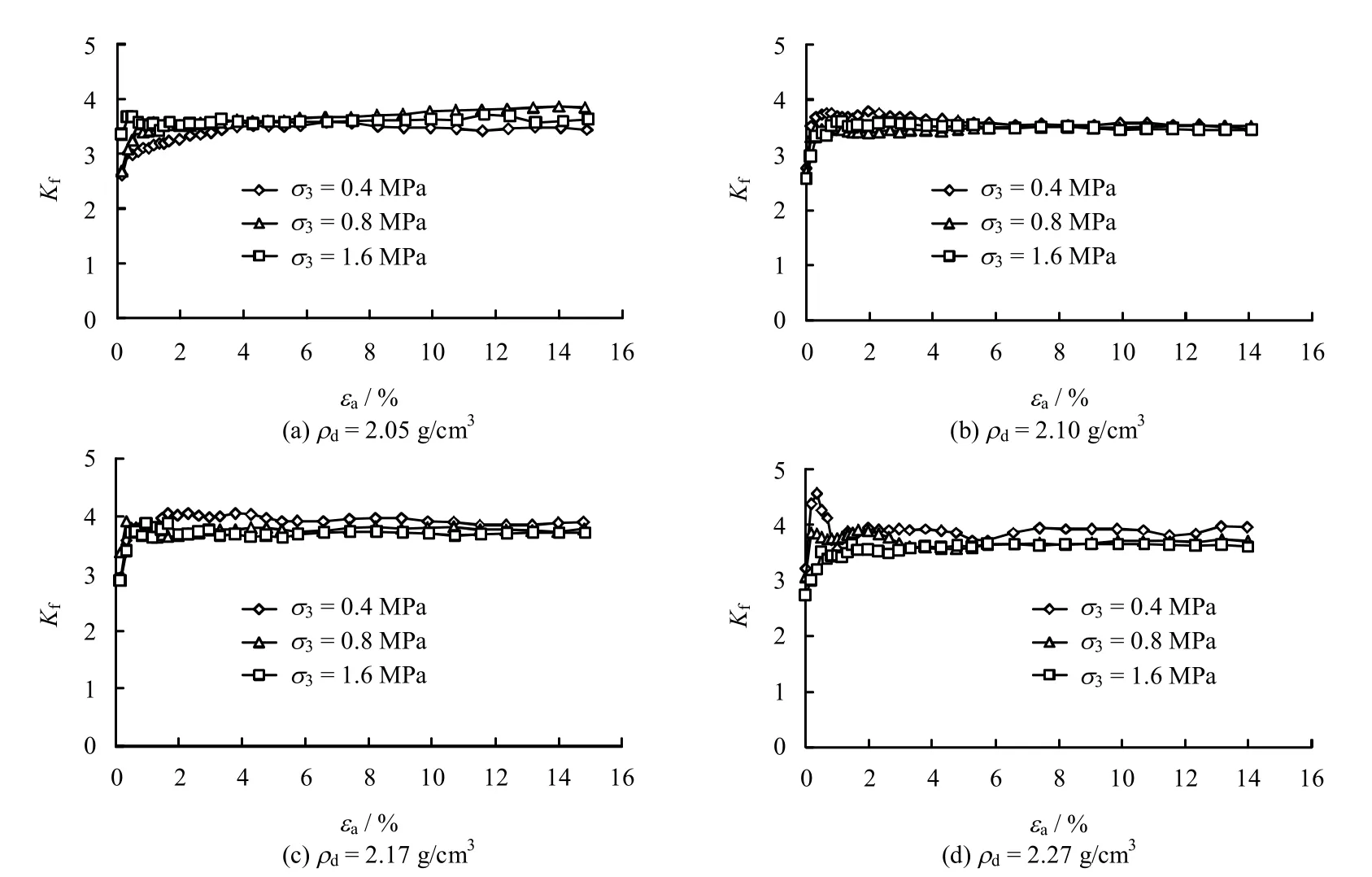
图10 Rowe 剪胀方程参数Fig.10 Parameters of Rowe dilatancy equation

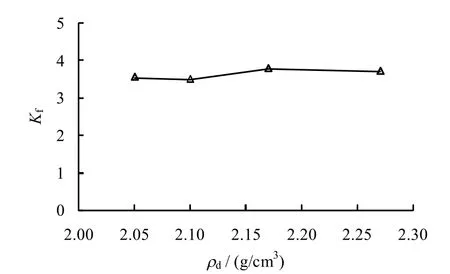
图11 Rowe 剪胀方程参数平均值Fig.11 Average value of parameters of Rowe dilatancy equation

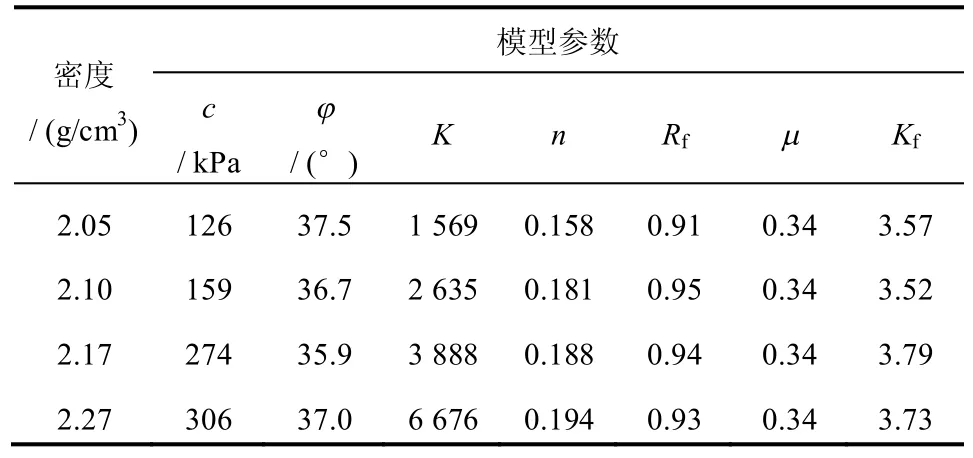
表1 非线性剪胀模型参数Table 1 Parameters of nonlinear dilatancy model

6 剪应力引起的体变

图12为非线性剪胀模型计算得到的塔城砂砾石剪应力引起的体变。

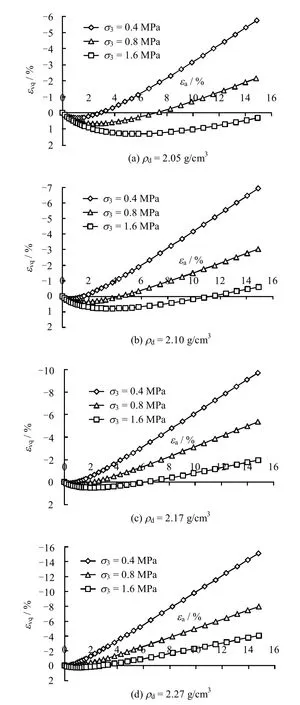
图12 剪应力引起的体变Fig.12 Volumetric strain caused by shear stress

从图12 中可以看出，剪应力引起的体变并不总是膨胀的，一般是先压缩后膨胀，具有普遍性，这与一般观点认为剪胀都是体积膨胀有所不同。由图还可以看出，围压越小，剪应力引起的体缩越小，而体胀越大且压缩阶段在剪切中也明显变短，说明围压越小，对于抑制粗粒土的体积膨胀是不利的。密度越大，剪应力引起的体积膨胀越大，特别是在低围压下初始剪切阶段土体压缩量很小，或基本不具压缩过程，很快转到膨胀阶段。

7 压缩速率

若将压应力引起的体变增量与轴向应变增量之比（dεvp/dεa）称为压缩速率，表示压应力引起体变的压缩性；将剪应力引起的体变增量与轴向应变增量之比的负值（-dεvq/dεa）称为剪胀速率，表示剪应力引起体变的剪胀性。则体变的变化趋势和大小取决于压缩速率（压缩性）和剪胀速率（剪胀性）的大小。

图13为根据剪胀模型计算的压应力引起体变的压缩速率（dεvp/dεa）随轴向应变的变化。由图可以看出，本次试验的塔城砂砾石压缩速率基本不随应力状态的变化而变化，也不随围压和初始干密度的变化而变化，稳定在某一常数，反映了塔城砂砾石在压应力下的压缩特性，对于本文试验的塔城砂砾石压缩速率为0.35 左右。对于其它粗粒土是否也有这种特性，本文限于试验成果的限制，有必要在以后的研究中积累资料进一步研究和验证。

8 剪胀速率

图14为根据剪胀模型计算的剪应力引起的体变速率或剪胀速率（-dεvq/dεa）。由图可以看出，剪胀速率均是从一负值开始增加，最终增大到一正值，说明剪应力引起的体变一开始是压缩的，随后才产生体积膨胀，剪胀速率为0 的那一点为剪缩和剪胀的转变点，即对应于剪应力引起的体积变化由压缩变为膨胀。围压越小，或密度越大，剪胀速率曲线越陡，剪胀速率为0 时轴向应变越小，表明剪胀速率越大，剪应力引起的体胀变形也越大，这种状态的粗粒土的剪胀性越大。较高围压下剪胀速率曲线基本均为单调增加，对应于硬化型的应力-应变曲线；低围压下剪胀速率曲线均呈现出先增大后减小的变化规律，与软化型的应力-应变曲线相对应。图中水平实线为压应力引起的体变速率或称为压缩速率（dεvp/dεa）。4 种不同密度的塔城砂砾石压缩速率基本相同，约为0.35，若剪胀速率小于压缩速率，表明压应力引起的体积压缩大于剪应力引起的体积膨胀，即压缩性大于膨胀性，体变一直是压缩的，此时剪胀速率曲线单调增加，并位于压缩速率水平线的下方，应力-应变曲线为硬化型。若剪切后期剪胀速率曲线在压缩速率水平线的上方，说明剪应力引起的体积膨胀大于压应力引起的体积压缩，体变后期是膨胀的，此时剪胀速率增大到最大值后又有所减小，但仍大于压缩速率，剪胀速率曲线位于压缩速率水平线的上方，应力-应变曲线表现为软化型，有明显的峰值强度。因此，粗粒土的剪胀性与应力-应变关系是密切相关的。

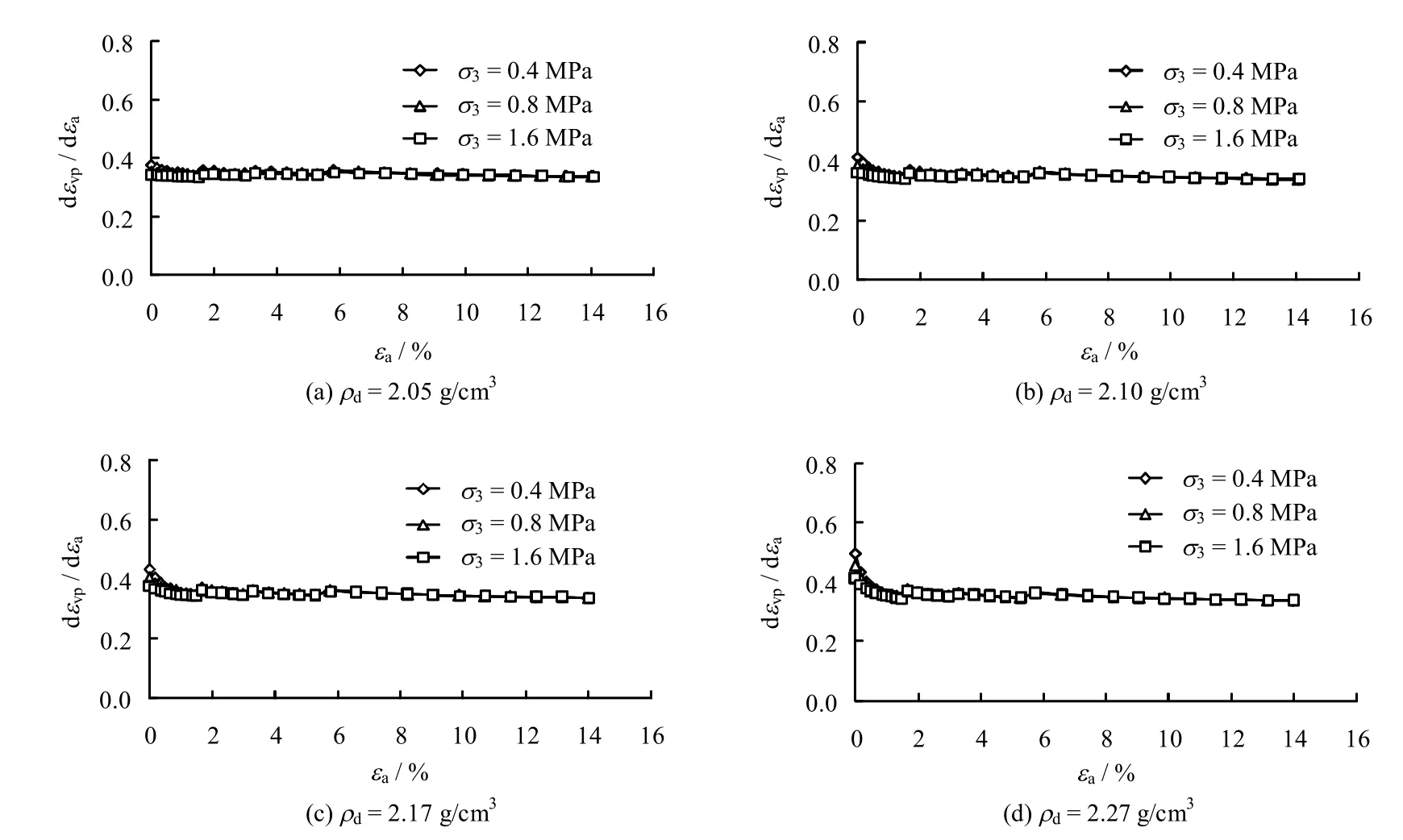
图13 压应力引起的体变速率Fig.13 Volumetric strain rates caused by compression stress

图14 剪应力引起的体变速率Fig.14 Volumetric strain rates caused by shear stress

9 结 论

（1）若体变增量与轴向应变增量之比先从正值减小到负值后又有所增大但仍小于0，则应力-应变曲线为软化型。比值为最小值时，土体剪胀性最大，对应于峰值强度，若体变增量与轴向应变增量之比单调减小并大于0，则应力-应变曲线为硬化型；

（2）体变变化趋势取决于剪胀性和压缩性的大小，剪切后期若剪胀速率先增大后减小并大于压缩速率，则体变是先压缩后膨胀的，应力-应变曲线呈现软化型，有明显的峰值强度。反之，若剪胀速率单调增大并小于压缩速率，则体变一直是压缩的，应力-应变曲线表现为硬化型。

认识粗粒土的剪胀性的变化规律以及剪胀性与应力-应变性质的关系，对于加深了解粗粒土的工程特性，可为工程分析提供合理依据具有重要的应用价值。

[1]魏汝龙.论土的剪胀性[J].水利学报,1963,8(6):31-40.WEI Ru-long.Discussion on dilatancy of soils[J].Journal of Hydraulic Engineering,1963,8(6):31-40.

[2]HENKEL D J.The relationships between the effective stresses and water content in saturated clays[J].Geotechnique,1960,10(2):41-54.

[3]PARRY R H G.Triaxial compression and extension tests on remoulded saturated clay[J].Geotechnique,1960,10(4):166-180.

[4]FROSSARD E.Effect of sand grain shape on interparticle friction:indirect measurements by Rowe's stress dilatancy theory[J].Geotechnique,1979,29(3):341-350.

[5]BOLTON M D.The strength and dilatancy of sands[J].Geotechnique,1986,36(1):65-78.

[6]LI X S,DAFALIAS Y F.Dilatancy for cohesionless soils[J].Geotechnique,2000,50(4):449-460.

[7]NG T-T.Fabric evolution of ellipsoidal arrays with different particle shapes[J].Journal of Engineering Mechanics,2001,127(10):994-999.

[8]LIU S,MATSUOKA H.Microscopic interpretation on a stress-dilatancy relationship of granular materials[J].Soils and Foundations,2003,43(3):73-84.

[9]BEEN K,JEFFERIES M.Stress-dilatancy in very loose sand[J].Canadian Geotechnical Journal,2004,41(5):972-989.

[10]POWRIE W,NI Q,HARKNESS R,ZHANG X.Numerical modelling of plane strain tests on sands using a particulate approach[J].Geotechnique,2005,55(4):297-306.

[11]SIMONI A,HOULSBY G T.The direct shear strength and dilatancy of sand-gravel mixtures[J].Geotechnical and Geological Engineering,2006,24(3):523-549.

[12]LEE J,EUN J,LEE K,et al.In-situ evaluation of strength and dilatancy of sands based on CPT results[J].Soils and Foundations,2008,48(2):255-265.

[13]杨迎晓,龚晓南,范川,等.钱塘江冲海积非饱和粉土剪胀性三轴试验研究[J].岩土力学,2011,32(增刊1):38-43.YANG Ying-xiao,GONG Xiao-nan,FAN Chuan,et al.Triaxial testing study of dilatants characteristics of Qiantangjiang alluvial unsaturated silts[J].Rock and Soil Mechanics,2011,32(Supp.1):38-43.

[14]褚福永,朱俊高,殷建华.基于大三轴试验的粗粒土剪胀性研究[J].岩土力学,2013,34(8):2249-2254.CHU Fu-yong,ZHU Jun-gao,YIN Jian-hua.Study of dilatancy behaviors of coarse-grained soils in large-scale triaxial test[J].Rock and Soil Mechanics,2013,34(8):2249-2254.

[15]姜景山,刘汉龙,程展林,等.密度和围压对粗粒土力学性质的影响[J].长江科学院院报,2009,26(8):46-50.JIANG Jing-shan,LIU Han-long,CHENG Zhan-lin,et al.Influences of density and confining pressure on mechanical properties for coarse-grained soils[J].Journal of Yangtze River Scientific Research Institute,2009,26(8):46-50.

[16]程展林,丁红顺.论堆石料力学试验中的不确定性[J].岩土工程学报,2005,27(10):1222-1225.CHENG Zhan-lin,DING Hong-shun.Research on indeterminacy of rockfill test result[J].Chinese Journal of Geotechnical Engineering,2005,27(10):1222-1225.

[17]程展林,姜景山,丁红顺,等.粗粒土非线性剪胀模型研究[J].岩土工程学报,2010,32(3):460-467.CHENG Zhan-lin,JIANG Jing-shan,DING Hong-shun,et al.Nonlinear dilatancy model for coarse-grained soils[J].Chinese Journal of Geotechnical Engineering,2010,32(3):460-467.

[18]ROWE P W.The stress-dilatancy relation for static equilibrium of an assembly of panicles in contact[J].Proceedings of The Royal Society(Series A),1962,269:500-527.

[19]钱家欢,殷宗泽.土工原理与计算(第二版)[M].北京:中国水利出版社,1996:54-60.

[20]迟世春,贾宇峰.土颗粒破碎耗能对罗维剪胀模型的修正[J].岩土工程学报,2005,27(11):1266-1269.CHI Shi-chun,JIA Yu-feng.Rowe’s stress-dilatancy model modified for energy dissipation of particle breakage[J].Chinese Journal of Geotechnical Engineering,2005,27(11):1266-1269.

[21]张丙印,贾延安,张宗亮.堆石体修正Rowe 剪胀方程与南水模型[J].岩土工程学报,2007,29(10):1443-1448.ZHANG Bing-yin,JIA Yan-an,ZHANG Zong-liang.Modified Rowe’s dilatancy law of rockfill and Shen Zhujiang’s double yield surfaces elastoplastic model[J].Chinese Journal of Geotechnical Engineering,2007,29(10):1443-1448.

[22]徐明,宋二祥.粗粒土的一种应变硬化模型[J].岩土力学,2010,31(9):2967-2973.XU Ming,SONG Er-xiang.A strain hardening model for rockfills[J].Rock and Soil Mechanics,2010,31(9):2967-2973.

[23]米占宽,李国英,陈生水.基于破碎能耗的粗颗粒料本构模型[J].岩土工程学报,2012,34(10):1801-1811.MI Zhan-kuan,LI Guo-ying,CHEN Sheng-shui.Constitutive model for coarse granular materials based on breakage energy[J].Chinese Journal of Geotechnical Engineering,2012,34(10):1801-1811.

[24]孙海忠.基于细观理论的粗粒土剪胀性及本构模型[J].同济大学学报(自然科学版),2012,40(12):1783-1788.SUN Hai-zhong.Dilatancy of coarse aggregates and its modeling based on micro theory[J].Journal of Tongji University(Natural Science),2012,40(12):1783-1788.