列车振动荷载作用下南京细砂累积变形预测公式对比分析

沈礼伟，庄海洋，陈 磊，李 浩

（1.南京工业大学 岩土工程研究所，南京 210009；2.江苏省交通规划设计院股份有限公司，南京 210005）

1 引 言

我国城市轨道交通发展之快，规模之大，是世界罕见的，但在轨道交通建设与运营过程中存在着较多的重大工程技术问题，工程实践先于理论的矛盾十分突出，其中列车运行引起的路基长期沉降问题就是这些重大工程技术难题之一。根据我国轨道交通的中长期规划，越来越多的轨道交通线会建造在深厚的新近沉积松散砂土、饱和软黏土等松软地基上，在轨道交通运行振动引起的往返荷载作用下地基振动孔隙水压力上升，塑性变形累积，很可能产生很大的长期附加沉降。

目前国内外学者对各类土在交通荷载下的长期附加沉降进行了研究，砂土的研究方法通常有3 种，第一种是通过室内试验，对重塑土样进行模拟交通荷载作用的循环三轴试验，研究土在长期循环荷载作用下的动力学特性[1-2]；第二种是建立本构模型，借助有限元分析软件模拟交通荷载研究土的长期沉降[3-4]；第三种是经验拟合的方法，建立拟合曲线或者总结出累积变形公式，研究土体累积变形与土的初始固结特性、静应力状态、动应力及循环次数的关系[5-6]。经验拟合公式，很早就引起学者们重视，对于不同土体已经建立了很多经验公式，并能很好地拟合对应土体的残余变形特性。广泛应用的预测公式中是Manumit 等[7]提出的指数模型，由于其考虑的影响因素较少，拟合效果相对较差，因此Li 等[8]对模型进行了改进。除了指数模型，还有一些其他学者提出了具有较好拟合效果的经验公式，如Parr[9]提出的残余应变模型以及庄海洋等[10]提出的对数模型。

本文首先对一些国内外学者提出的累积变形公式进行总结归纳，并以新近沉积南京细砂为研究对象，通过对比预测公式计算结果与室内三轴试验数据研究了南京细砂累积变形的经验拟合公式，并对部分公式进行了修正和计算能力的扩展，给出了相关公式中对应的模型参数建议值。

2 累积变形的预测公式

Li 等[8]通过室内试验对Monismith 指数模型进行了改进，引入土体静力强度参数，考虑了土的静强度和动偏应力的影响，解决了Monismith 指数模型参数取值范围大的缺点，其表达式为

式中：qd试验的动应力；qf为试验土体的静强度；a、m、b为试验参数。

黄茂松等[11]在Parr 的残余应变模型基础上对其进行了修正，通过对塑性应变进行归一化处理，提出了第一次循环塑性应变，将循环加载动应力大小和应力历史等因素的影响包含在第一次循环加载塑性应变中，其表达式为

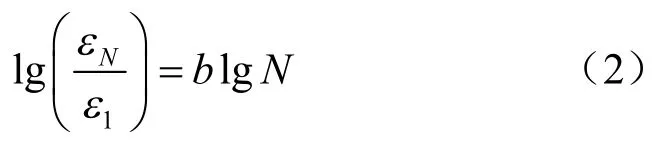
式中：εN为第N 次循环的塑性应变；ε1为第一次循环加载的塑性应变；b为试验常数。

张勇等[12]在指数模型基础上考虑一定循环周次后累积塑性应变趋于稳定的规律，提出了用数学方程来拟合累积塑性应变与循环周次的关系曲线，其表达式为

式中：N为循环周次；a、b、c为与应力条件和土的性质有关的参数，其中a c 具有累积塑性应变极限值的物理意义，b 反映累积塑性应变曲线形状，并在一定情况下可定义为常数。

庄海洋等[10]通过幂指对数函数拟合交通荷载作用下砂土样累积应变曲线，提出了不排水条件累积竖向应变的预测公式：

式中：k为待定系数；m为根据相同振动加载幅值时不同围压条件下累积应变增长规律确定的影响指数；n为根据同围压时不同振动加载幅值条件下累积应变增长规律确定的影响指数；p、q为根据试样累积应变增长曲线拟合确定的竖向应变累积特征参数；σc为试样加载围压；qd为振动加载幅值；Nd为列车振动列次；Pa为一个标准大气压。

3 试验结果与预测公式的对比分析

3.1 试验概况

试验采用南京工业大学土木工程与防灾减灾实验室内的GDS 空心圆柱扭剪仪，能独立控制轴向、扭矩、内压和外压4 个循环荷载，土样尺寸（直径×高）为10 cm×20 cm，最大围压为2.0 MPa，最大动态扭转角度可达1 080°，可进行实心、空心土样在复杂应力路径下静、动力试验。该仪器对试样可施加4 个独立的荷载，即轴力W、扭矩MT、内围压 pi和外围压 p0，试验仪器与加载应力路径如图1 所示。

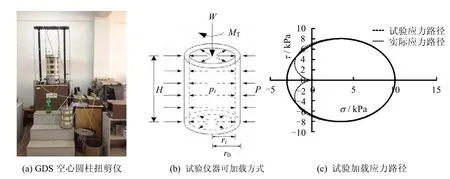
图1 试验仪器与加载应力路径Fig.1 Test instrument and loading stress path

试验土样为南京细砂，对粉细砂进行重塑，基本物理指标为：平均天然重度ρ=18.5 kN/m3，最大孔隙比 emax=1.14，最小孔隙比 emin=1.14，不均匀系数 Cu=2.31，曲率系数 Cc=1.07。对应的颗粒级配曲线图如图2 所示，重塑土样相对密度 Dr=0.5。

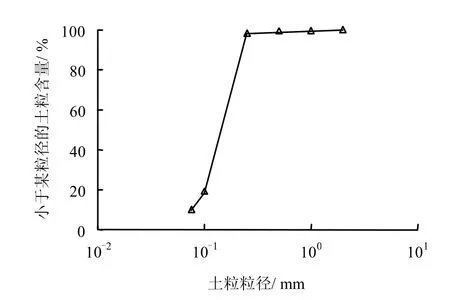
图2 南京细砂的颗粒级配曲线Fig.1 Grain size distribution diagram of Nanjing fine sand

采用三瓣铜模制样器制备砂土试样，分4 层装样，逐层击实至控制重塑样指标，制成均为内直径为60 mm，外直径为100 mm，高为200 mm 试样。制备完成后，首先采用抽气通循环水进行饱和，直至连续10 min 内不出现气泡。将此时制备好的试样安装到GDS 循环仪上，采用压力控制器将反压控制在100～150 kPa 范围内，继续通循环水进行饱和，直至没有气泡冒出，调整内压、外压和反压，测得有效围压接近预定值时开始固结。达到有效围压并固结完成后即施加循环荷载，开始振动特性试验。具体试验方案见表1。

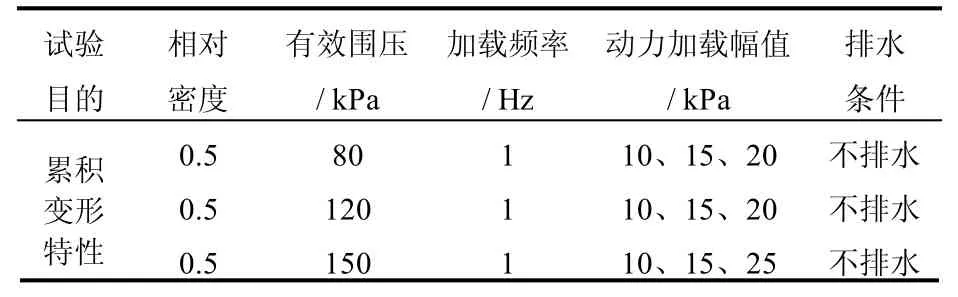
表1 试验加载方案Table 1 The test load plan

3.2 心型应力路径与椭圆应力路径试验结果对比

受试验仪器等条件限制，无法在各种试验条件下较好地完成心型应力路径加载，故本次试验对心型应力路径进行了简化，采用椭圆形应力路径进行代替，如图1(c)中所示。图3为两种应力路径下竖向应变增长情况的对比，从图中可以发现，在加载幅值为10、15、25 kPa 时，两种应力路径下竖向应变增长趋势十分接近，增长幅度基本相同，100 列次之后的累积竖向应变最大偏差出现在加载幅值25 kPa 时，而此时的差值也仅为0.022%。由于试验仪器影响及制样装样过程中不可避免地存在一定偏差，因此，两者竖向应变的增长过程中存在较小的差值属于正常现象。

在此分析基础上可以初步得到结论：在模拟交通荷载作用对土体竖向应变的影响时，椭圆应力路径可以代替心型应力路径。

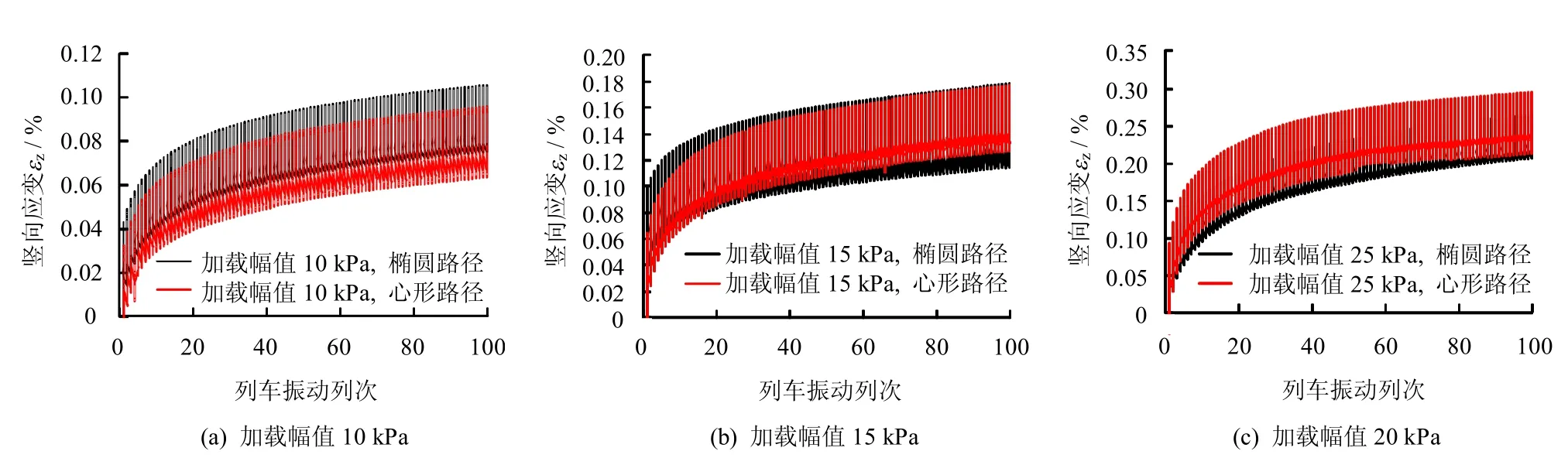
图3 有效围压120 kPa 时式（1）～（3）预测结果与试验数据对比Fig.3 Predicted results by formula(1)-(3) when the effective confining pressure is 1200kPa

3.3 公式与试验结果对比分析

上述所列累积塑性应变预测公式（1）～（4）为目前国内外学者较认可的主要预测方法，部分公式是对已有公式的改进，可将其分为三类：指数模型、对数模型和幂指对数模型。本文分别从三类预测模型中选取表2 中4 个公式进行对比研究，其中式（1）～（3）是直接计算累积应变，而式（4）表达的是应变速率与加载变量之间的关系。本文分别以应变及应变率进行分析比较。

公式中参数取值方法：式（1）中考虑到了围压及加载幅值的影响，只需取1 组参数用于9 个工况，式（2）、（4）中未考虑围压的影响，只能分别在3种围压下各取1 组参数来分别拟合不同试验围压下的试验结果。在围压80 kPa和加载幅值10 kPa 的试验数据中，以3 个公式在100 振次时交于一点为标准，确定公式的拟合参数值，式（1）中该参数取值在9 个工况下保持恒定。式（2）中该参数取值作为围压80 kPa 3 个工况下保持不变，围压120 kPa 及150 kPa 时参数取值均在加载幅值10 kPa 时以3 个公式于100 振动列次（700 振次）交于一点为标准。式（3）参数在9 个工况中取值均不同，每个工况中取值均是以3 个公式于100 振动列次交于一点为标准进行的。式（4）中参数的取值也分别在3 种围压加载幅值10 kPa 下，以首尾两点（N=1 及N=100）为标准确定。

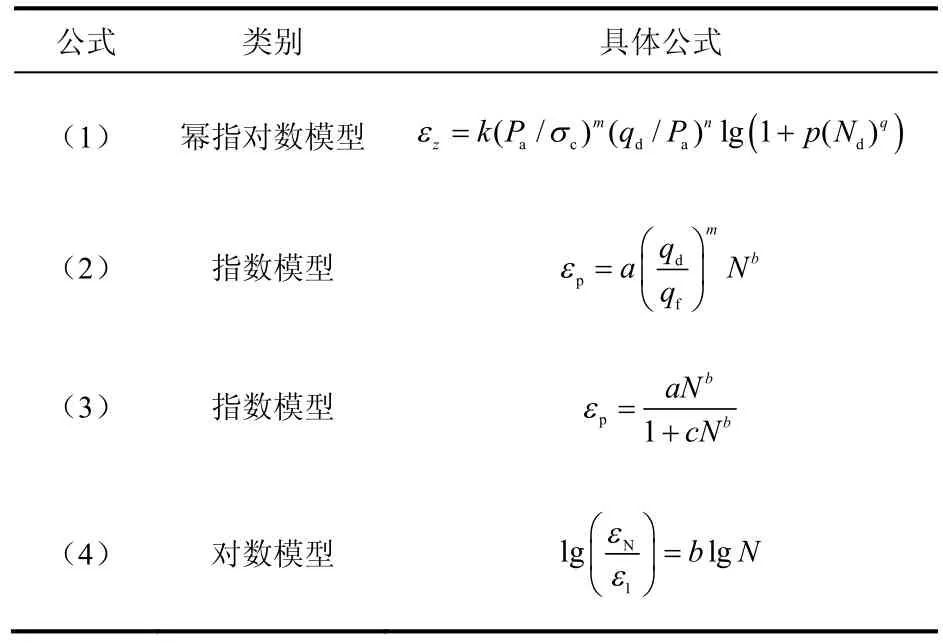
表2 对比分析所选公式Table 2 The selected formulas for contrastive analysis

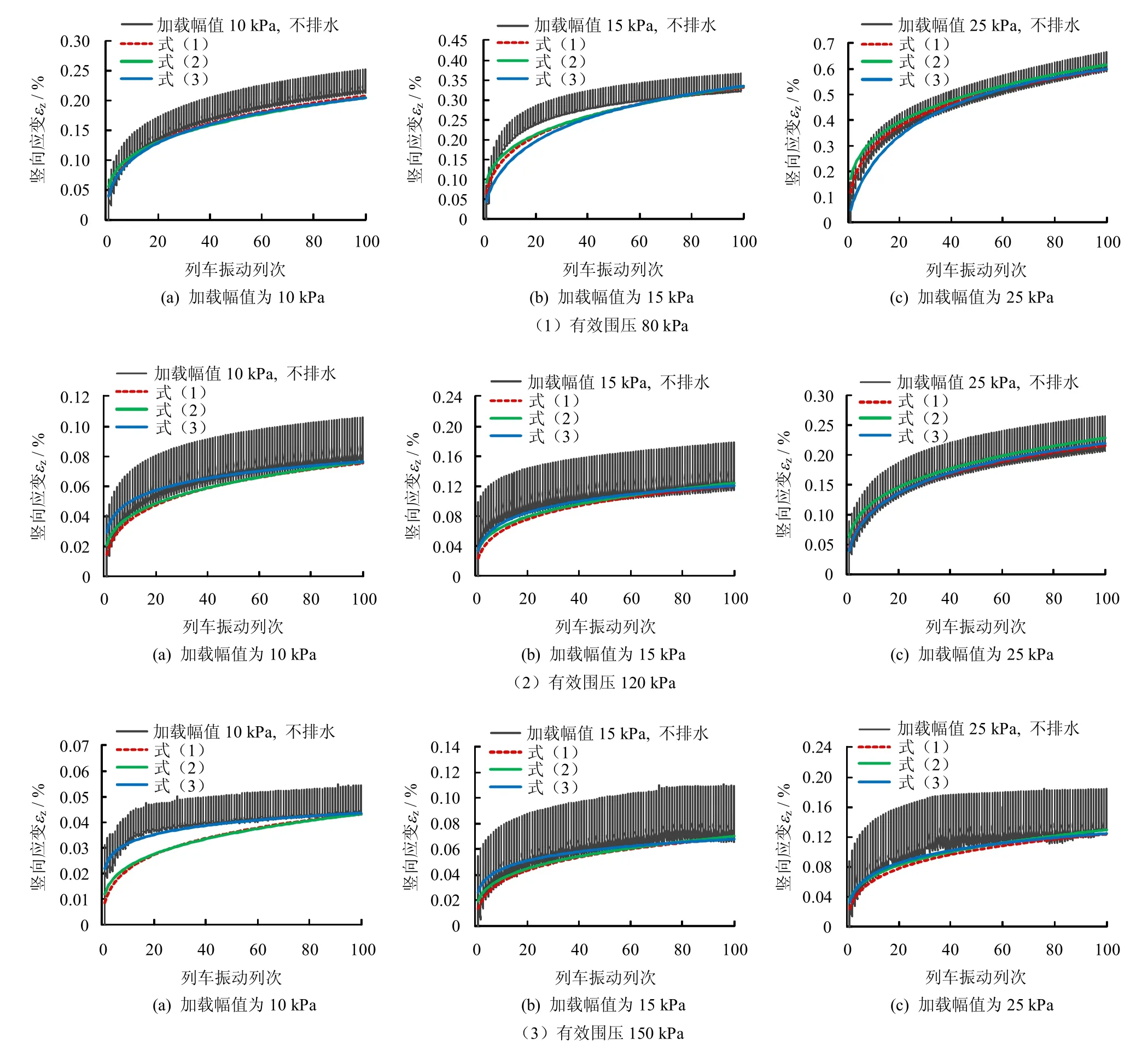
图4 不同围压时式（1）～（3）预测结果与试验数据对比Fig.4 Predicted results by formula(1)-(3) when different effective confining pressures

图4为不同试验围压下的试验结果与公式的预测结果对比分析，总体来看，随着加载幅值的增加，式（1）～（3）对100 振动列次（700 振次）后土样最终累积竖向应变的预测结果很接近。随着加载幅值的增加，式（2）的预测结果逐渐增加到最大，式（1）的预测结果则逐渐变到最小。同时，式（1）～（3）对高加载幅值（25 kPa）试验结果的预测效果明显要比低应变幅值的预测效果要好。由此可以认为，以前主要用于黏土动力累积变形的相关预测公式也可用于列车振动荷载作用下南京细砂的动力累积变形的预测分析，本文分别给出了各预测公式对应的模型参数建议值，见表3、4。

表3 模型参数建议值Table 3 The suggested values of parameters in formulas

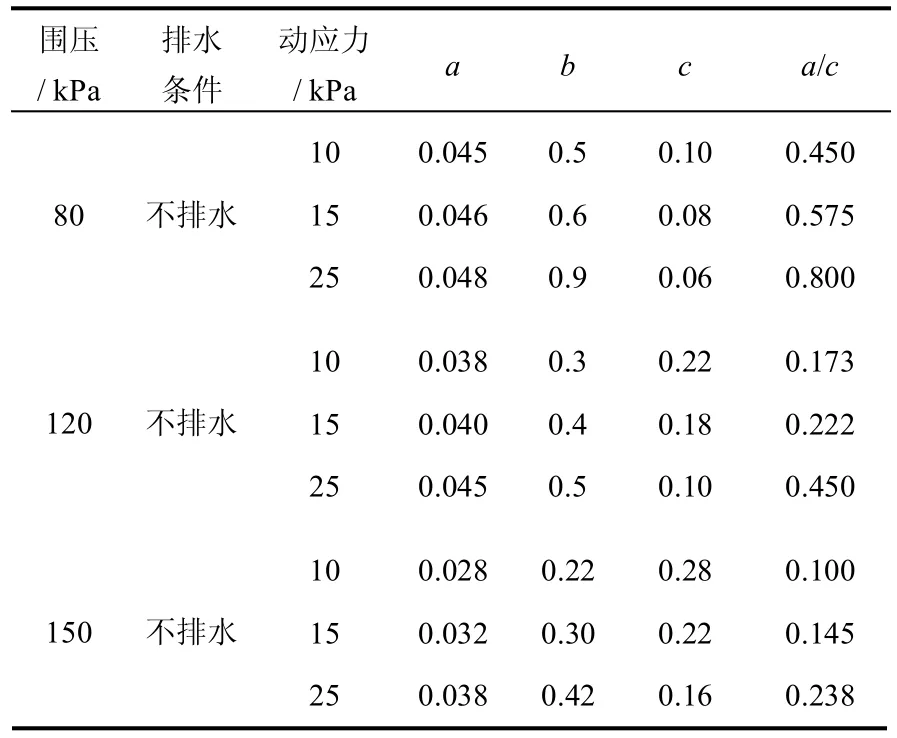
表4 式（3）参数建议值Table 4 The suggested values of parameters by formula(3)

图5为所有工况应变速率与式（4）的预测结果对比。总体来看，lg（εNε1）随着lg N 的增长呈现出线性递减的规律，与式（4）预测结果相近，但试验数据与公式预测不可避免地存在一定差异。

式（3）对应每个工况都有不同的参数，见表4。由表中可以看出，参数a、b、c 值的变化有一定规律性，与张勇等[8]通过不排水动三轴试验所得到的规律一致。从拟合参数与动应力幅值的关系（见图6）中可以发现，随着动应力幅值的增加，参数b、c、a/c 大致呈线性变化，经拟合得到：参数b 在围压为80、120、150 kPa 时对应的斜率分别为0.027、0.013、0.013；参数c 在围压为80、120、150 kPa时对应的斜率分别为-0.003、-0.008、-0.008；参数a/c 在围压为80、120、150 kPa 时对应的斜率分别为0.023、0.018、0.009。

式（2）、（4）未考虑土样有效围压对其累积变形的影响，根据本次试验结果所得有效围压与累积变形的关系，对式（2）、（4）进行了初步修正，使两个公式能够考虑有效围压得影响，修正后公式为

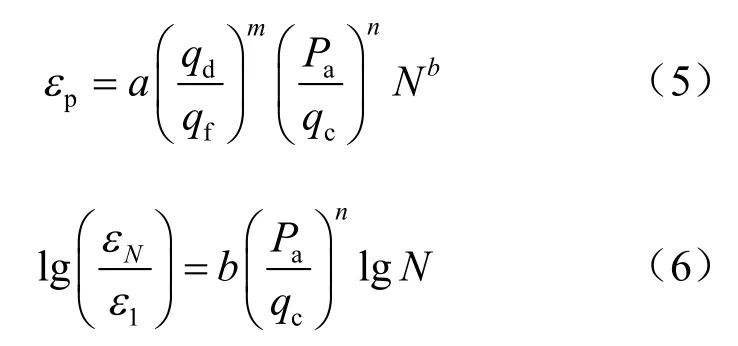
对应于试验数据，修正后公式可应用于考虑有效围压的累积变形预测，基于表3 中数据可以确定式（5）、（6）中的参数为

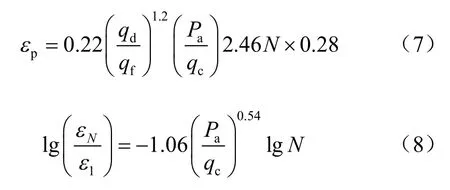
4 结 语

通过两种不同应力路径下试验结果的对比分析，证明在模拟交通荷载作用对土体竖向应变的影响时，椭圆应力路径可以代替心型应力路径，这样就可以增强现有试验仪器在高频条件下模拟列车振动荷载应力的加载能力。

以前主要用于黏土动力累积变形的相关预测公式也可用于列车振动荷载作用下南京细砂的动力累积变形的预测分析，针对南京细砂的试验结果，本文分别给出了各预测公式对应的模型参数建议值。

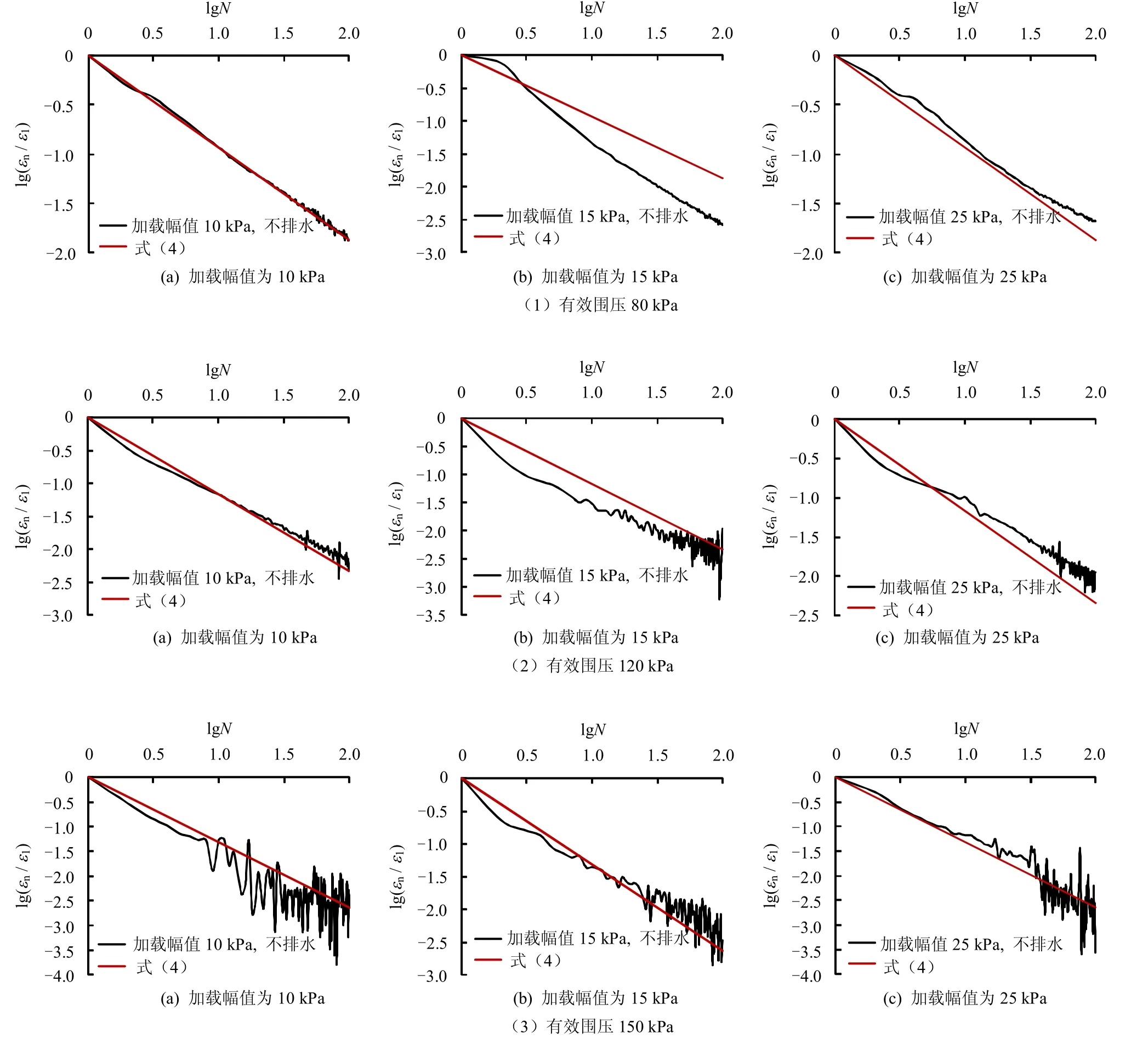
图5 不同围压时式（4）预测结果与试验数据对比Fig.5 Predicted results by formula(4) when different effective confining pressures

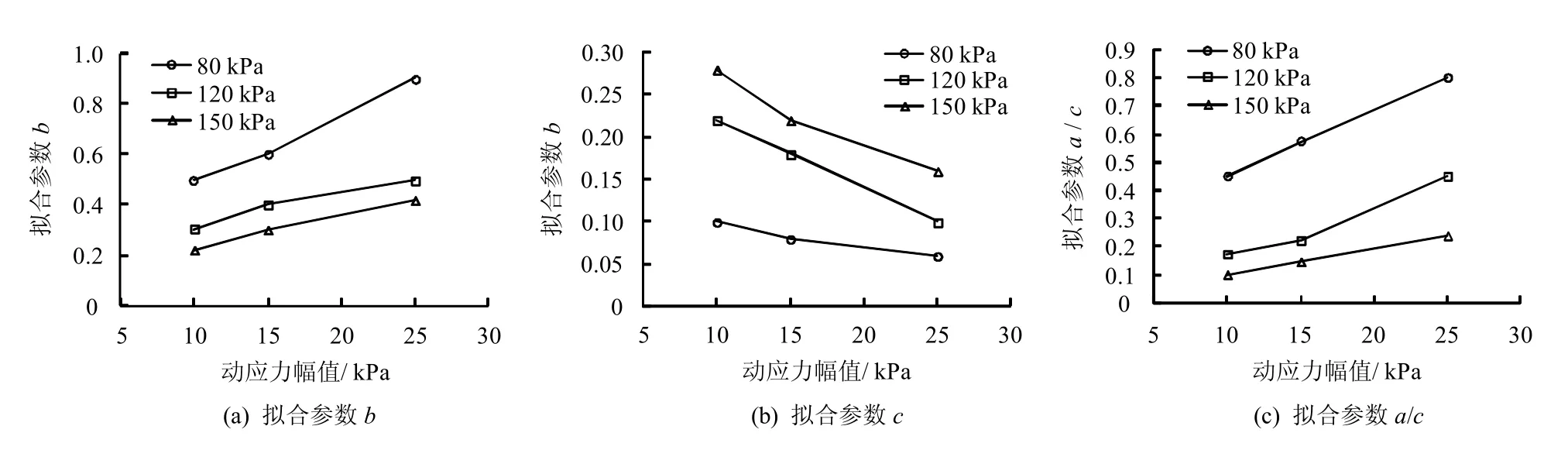
图6 式（4）中拟合参数与动应力幅值关系Fig.6 Relationships between fitting parameters and dynamic stress amplitude in formula(4)

根据本文对南京细砂累积变形的试验结果所得有效围压与累积变形的关系，对部分公式进行了初步修正，即使之能够考虑有效围压的影响，并给出了具体的拟合参数建议值。

[1]雷华阳,姜岩,陆培毅,等.交通荷载作用下结构性软土动本构关系的试验研究[J].岩土力学,2009,30(12):3788-3792.LEI Hua-yang,JIANG Yan,LU Pei-yi,et al.Experimental study of dynamic constitutive relation of structural soft soils under traffic loading[J].Rock and Soil Mechanics,2009,30(12):3788-3792

[2]黄博,丁浩,陈云敏,等.交通荷载作用后粉质黏土不排水强度特性试验研究[J].岩石力学与工程学报,2010,29(增刊2):3986-3993.HUANG Bo,DING Hao,CHEN Yun-min,et al.Experimental study of undrained strength property of saturated silty clay after traffic load[J].Chinese Journal of Rock Mechanic and Engineering,2010,29(Supp.2):3986-3993.

[3]魏星,王刚,余志灵.交通荷载下软土地基长期沉降的有限元法[J].岩土力学,2010,31(6):2011-2015.WEI Xing,WANG Gang,YU Zhiling.FEM of traffic-load-induced settlement of road on soft clay[J].Rock and Soil Mechanics,2010,31(6):2011-2015.

[4]边学成,蒋红光,申文明,等.基于模型试验的高铁路基动力累积变形研究[J].土木工程学报,2011,44(6):112-119.BIAN Xue-cheng,JIANG Hong-guang,SHEN Wen-ming,et al.Study of accumulative deformation of high-speed railways based on physical model testing[J].China Civil Engineering Journal,2011,44(6):112-119.

[5]SHAHROUR I,MEIMON Y.Calculation of marine foundation subjected to repeated loads by means of the homogenization method[J].Computers and Geotechnics,1995,17:93-106.

[6]ABDELKRIM M,BONNET G,DE BUHAN P.A computational procedure for predicting the long term residual settlement of platform induced by repeated traffic loading[J].Computers and Geotechnics,2003,30:463-476.

[7]MONISMITH C L,OGAWA N,FREEME C R.Permanent deformation characteristics of subgrade soils due to repeated loading[J].Transport Research Record,1975,537:1-17.

[8]LI D,SELIG E T.Cumulative plastic deformation for fine-grained subgrade soils[J].Journal of Geotechnical Engineering,1996,122(12):1006-1013.

[9]PARR G B.Some aspects of the behavior of London clay under repeated loading[D].UK:University of Nottingham,1972.

[10]庄海洋,左玉峰,沈礼伟,等.列车振动荷载作用下南京细砂振动累积变形特性试验研究[J].工程地质学报,待刊.ZHUANG Hai-ang,ZUO Yu-feng,SHEN Li-wei,et al.The experimental study on vibration accumulated deformation characteristics of Nanjing fine sand under the train vibration loads[J].Journal of Engineering Geology,in press.

[11]黄茂松,李进军,李兴照.饱和软黏土的不排水循环累积变形特性[J].岩土工程学报,2006,28(7):891-895.HUANG Mao-song,LI Jin-jun,LI Xing-zhao.Cumulative deformation behaviour of soft clay in cyclic undrained tests[J].Chinese Journal of Geotechnical Engineering,2006,28(7):891-895

[12]张勇,孔令伟,郭爱国,等.循环荷载下饱和软黏土的累积塑性应变试验研究[J].岩土力学,2009,30(6):1542-1548.ZHANG Yong,KONG Ling-wei,GUO Aiguo,et al.Cumulative plastic strain of saturated soft clay under cyclic loading[J].Rock and Soil Mechanics,2009,30(6):1542-1548.