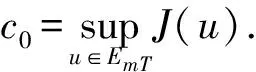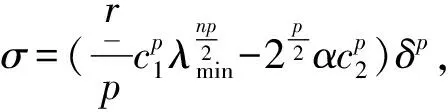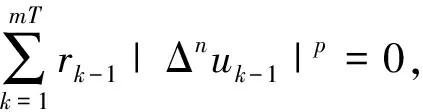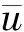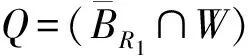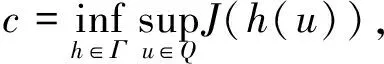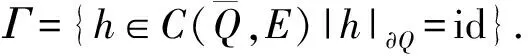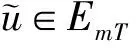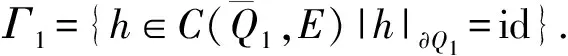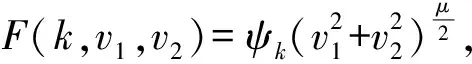2n阶非线性p-Laplacian型泛函差分方程的周期解
吴贤敏, 石海平
(广东建设职业技术学院 现代商务与管理系, 广东 广州 510450)
1 引言及主要结果
记N,Z及R分别表示自然数集、整数集和实数集.任取a,b∈Z满足a≤b,定义Z(a)={a,a+1,…},Z(a,b)={a,a+1,…,b}.*表示向量的转置.
考虑2n阶非线性泛函差分方程
Δn(rk-nφp(Δnuk-1))=(-1)nf(k,uk+M,uk,uk-M),
n∈Z(1),k∈Z
(1)
周期解的存在性.其中,Δ是向前差分算子Δuk=uk+1-uk,Δ2uk=Δ(Δuk),rk>0是Z上的实值函数,φp(s)是p-Laplacian算子φp(s)=|s|p-2s(1 方程(1)可以看作下列非线性泛函微分方程的离散类似 (-1)nf(t,u(t+M),u(t),u(t-M)), t∈R. (2) 对于非线性泛函微分方程的研究,在应用和理论上都有十分重要的意义[1-5]. 众所周知,差分方程跟微分方程一样,也是对现实世界的一些现象的一种描述.近年来,差分方程已广泛出现在科学研究的各个领域中,如概率论、矩阵论、电路分析、组合分析、排队论、数论、心理学与社会学等[6-10].而且,由于在生产实际和科学研究中所遇到的微分方程往往很复杂,在很多情况下都不可能给出解的解析表达式,为了数值模拟的需要,常常需要将微分方程加以离散化,研究其相应的差分方程.因此,理论和实际的需要使得差分方程理论得到迅速的发展.文献[11]考虑了具有滞后、超前项的泛函差分方程的单调迭代技术,文献[12-13]研究了具有超前和滞后的泛函差分方程同宿轨的存在性.本文将应用临界点理论给出2n阶非线性p-Laplacian型泛函差分方程(1)周期解存在性和多重性的充分条件,所得结果推广和改进了文献[14-15]相关结果.所采用的方法主要是利用环绕定理结合变分技巧.研究的主要结果如下. 定理1.1假设下列条件满足: (F1) 对∀k∈Z,存在泛函F(k,v1,v2)∈C1(Z×R2,R)满足F(k,v1,v2)≥0,且 F(k+T,v1,v2)=F(k,v1,v2), 则对任意给定的正整数m>0,方程(1)至少存在2个非平凡mT-周期解. 注1.1由(F3)容易知道存在常数γ′>0,使得 事实上,令 易证所得的结论. 注1.2文献[14-15]获得当非线性项在超线性增长的条件下周期解的存在性,在(1)中分别取n=1,rk≡1,M=1及p=2,M=0,当非线性项在非超非次线性增长的条件下分别推出文献[14-15]的结果.因此,定理1.1推广并改进了文[14-15]的结果. 设S表示由所有如下形式的实数序列组成的向量空间, u={uk}k∈Z=(…,u-k,…,u-1,u0,u1,…,uk,…). 对任意的u,v∈S,a,b∈R,au+bv定义为 则S是向量空间. 对于给定的正整数m及T,定义S的子空间EmT为 EmT={u∈S|uk+mT=uk,∀k∈Z}. 显然,EmT与RmT同构.在EmT中定义内积 ∀u,v∈EmT. (3) 由此内积可诱导出空间EmT中的范数‖·‖为 ∀u∈EmT. (4) 显然,(EmT,〈·,·〉mT)是有限维Hilbert空间,且与RmT线性同构. 另一方面,对∀s>1,在EmT上定义‖·‖s为 ∀u∈EmT. (5) 由于‖u‖s与‖u‖2等价,存在常数c1,c2使得c2≥c1>0,且 c1‖u‖2≤‖u‖s≤c2‖u‖2, ∀u∈EmT. (6) 显然,‖u‖=‖u‖2.对∀u∈EmT,在空间EmT上定义泛函J (7) 显然,J∈C1(EmT,R)且对∀u={uk}k∈Z∈EmT,由u0=umT,u1=umT+1,得 f(k,uk+M,uk,uk-M). 因此,u是J在EmT上的临界点当且仅当 Δn(rk-nφp(Δnuk-1))=(-1)nf(k,uk+M,uk,uk-M), ∀k∈Z(1,mT). 由于u={uk}k∈Z∈EmT及rk,f(k,v1,v2,v3)关于k的周期性,因此,寻求方程(1)的mT-周期解问题就转化为寻求泛函J在EmT上的临界点.从而,泛函J在EmT上的临界点正好是方程(1)的古典mT-周期解. 设mT×mT矩阵P为 (8) 记W=kerP={u∈EmT|Pu=0∈RmT},则W={u∈EmT|u={c,c,…,c},c∈R}.令V是W关于EmT的正交补空间,即EmT=V⊕W.为方便起见,将u∈EmT与u=(u1,u2,…,umT)*看作是一致的. 设E是实的Banach空间,J∈C1(E,R),即J是定义在E上的连续Fréchet可微的泛函.称泛函J满足Palais-Smale条件(简称P.S.条件),如果对任意的序列{u(i)}⊂E,若{J(u(i))}有界且J′(u(i))→0(i→∞),则{u(i)}在E中存在收敛的子列.记Bρ为E上中心在原点半径为ρ的开球,∂Bρ为Bρ的边界. 引理2.1(环绕定理[16]) 设E是实的Banach空间,E=E1⊕E2,其中E1是E的有限维子空间.假设J∈C1(E,R)满足P.S.条件,并且 (J1) 存在常数a>0,ρ>0使得J|∂Bρ∩E2≥a; 引理2.2假设条件(F1)~(F3)成立,则J在EmT上有上界. 其中,x=(Δn-1u1,Δn-1u2,…,Δn-1umT).因为 所以 mTγ′≤mTγ′. 故存在常数K=mTγ′>0,使得对∀u∈EmT,J(u)≤K.证毕. 引理2.3假设条件(F1)~(F3)成立,则泛函J满足P.S.条件. 证明设{J(u(i))}是有下界的序列,即存在常数M1,使得对∀i∈N,-M1≤J(u(i)).由引理2.2的证明,易知 -M1≤J(u(i))≤ 因此 断言c0>0.事实上,由(F2)及引理2.2的证明过程知,对∀u∈V,‖u‖≤δ, 其中,x=(Δn-1u1,Δn-1u2,…,Δn-1umT)*.因为 所以 其中,y=(Δn-1e1,Δn-1e2,…,Δn-1emT)*.又因为 从而, 再一次应用环绕定理,J又存在临界值c′≥σ>0,其中 注3.1最后,给出一个例子来应用定理1.1.对∀n∈Z(1),k∈Z,假设 Δn(rk-nφp(Δnuk-1))= (9) [1] 郑祖庥. 非R.N.A.型泛函微分方程的近期进展[J]. 安徽大学学报:自然科学版,1994,35(1):11-30. [2] 林文贤. 一类中立型阻尼泛函微分方程的振动性[J]. 四川师范大学学报:自然科学版,2013,36(3):396-398. [3] 杨甲山,方彬. 一类二阶中立型微分方程的振动和非振动准则[J]. 四川师范大学学报:自然科学版,2012,35(6):776-780. [4] 杜瑞霞,刘萍. 一类带反馈控制的高维泛函微分方程的正周期解研究[J]. 四川师范大学学报:自然科学版,2012,35(1):16-20. [5] 周小平,卫星. 大型非线性偏泛函微分方程的不变集和吸引性[J]. 四川师范大学学报:自然科学版,2008,31(6):649-653. [6] Agarwal R P. Difference Equations and Inequalities: Theory, Methods and Applications[M]. New York:Marcel Dekker,1992. [7] Iannizzotto A, Radulescu V D. Positive homoclinic solutions for the discretep-Laplacian with a coercive weight function[J]. Differ Integral Equ Appl,2014,27(1/2):1-200. [8] Wang X P. New potential condition on homoclinic orbits for a class of discrete Hamiltonian systems[J]. Adv Difference Equ,2014,2014:1-9. [9] Chen H W, He Z M. Infinitely many homoclinic solutions for second-order discrete Hamiltonian systems[J]. J Difference Equ Appl,2013,19(12):1940-1951. [10] Chen W X, Yang M B, Ding Y H. Homoclinic orbits of first order discrete Hamiltonian systems with super linear terms[J]. Sci China Math,2011,54(12):2583-2596. [11] 田淑环,王文丽. 具有滞后、超前项的泛函差分方程的单调迭代技术[J]. 保定学院学报,2009,22(4):17-19. [12] Yu J S, SHI H P, Guo Z M. Homoclinic orbits for nonlinear difference equations containing both advance and retardation[J]. J Math Anal Appl,2009,352(2):799-806. [13] Chen P, Tang X H. Existence of many homoclinic orbits for fourth-order difference systems containing both advance and retardation[J]. Comput Math Appl,2011,217(9):4408-4415. [14] Chen P, Fang H. Existence of periodic and subharmonic solutions for second-orderp-Laplacian difference equations[J]. Adv Difference Equ,2007,2007:1-9. [15] Cai X C, Yu J S. Existence of periodic solutions for a 2nth-order nonlinear difference equation[J]. J Math Anal Appl,2007,329(2):870-878. [16] Rabinowitz P H. Minimax Methods in Critical Point Theory with Applications to Differential Equations[M]. Providence RI:Am Math Soc,1986.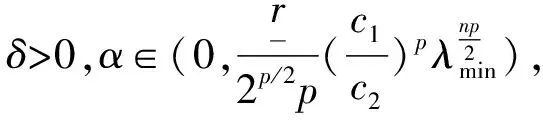
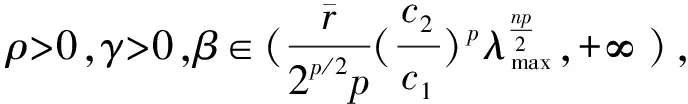
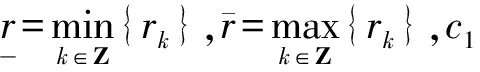

2 变分结构及基本引理

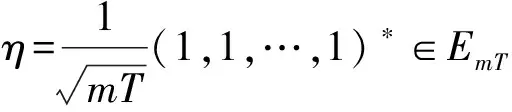
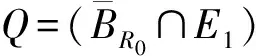
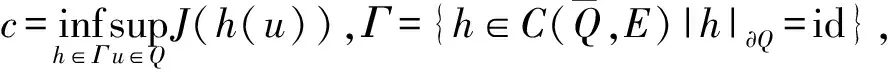

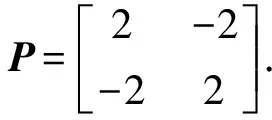
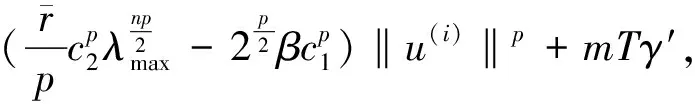
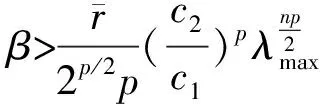
3 定理1.1的证明