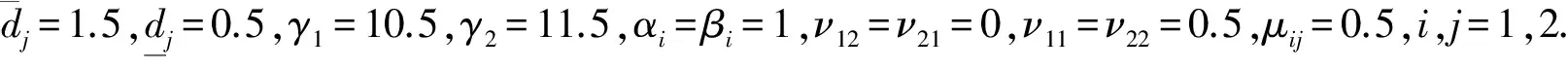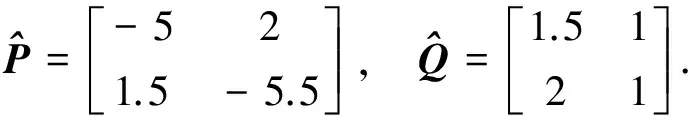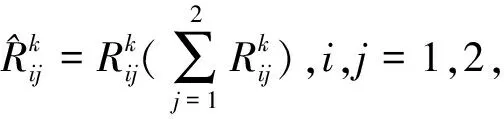变时滞Cohen-Grossberg脉冲随机反应扩散神经网络的吸引集

赵 雁

(乐山职业技术学院 电子信息工程系, 四川 乐山 614000)

自从1983年M. Cohen等[1]提出Cohen-Grossberg神经网络以来，由于它在信号和图像处理，联想记忆，组合优化等中的广泛应用，因此受到了广泛的关注和研究[2-13].由于脉冲，随机干扰和反应扩散，时滞Cohen-Grossberg脉冲随机反应扩散神经网络的平衡点往往不存在，这时,往往研究其吸引集的存在性[14-16].事实上，在实际应用当中,这种稳定就能够满足人们的需求[17].利用Ito公式，时滞微分不等式和M-矩阵性质,获得了变时滞Cohen-Grossberg脉冲随机反应扩散神经网络的吸引集存在的充分条件.

1 预备知识

为了方便，引入一些符号和定义.

Rn是实n维列向量空间.N{1,2,…,n}.R+[0,+∞).Rm×n记作m×n实矩阵集.用T记作n×n的单位矩阵.对A,B∈Rm×n或者A,B∈Rn,A≥B(A>B)表示A和B中的每一个对应元素都满足不等式“≥(>)”.特别地,如果矩阵A≥0和向量z>0,则他们分别被称为非负矩阵和正向量.E为数学期望.

令C[X,Y]表示从集合X到集合Y的连续映射集.并记CC[[-τ,0],Rn].

PC[X,Y]={φ(t):X→Y|φ(t)除可数点外函数连续,并且在这些可数点当中，函数φ(t)的左右极限φ-(t),φ+(t)存在，满足φ+(t)=φ(t)}.并记PCPC[[-τ,0],Rn].

对φ(t)∈C或φ(t)∈PC,定义

[φ(t)]τ=([φ1(t)]τ,…,[φn(t)]τ)T,

讨论如下变时滞Cohen-Grossberg脉冲随机反应扩散神经网络：

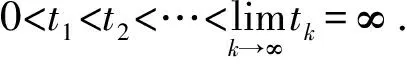
记u=(u1,…,un)T和L2(X)为标量值勒贝格可测函数集.记

为X的L2模.进一步，定义模‖u‖为

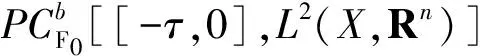
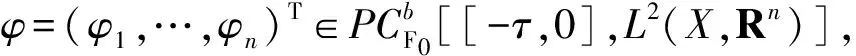
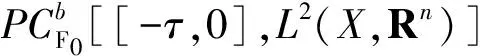
其中

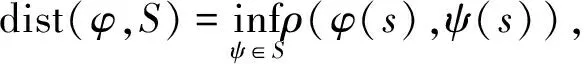
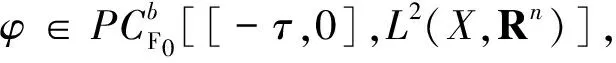
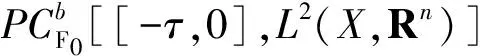
引理1.1[18]如果ai≥0,bi≥0,i∈N,p>0,q>0,并且1/p+1/q=1,那么

引理1.2设J是非负向量，P=(pij)n×n，其中pij≥0(i≠j),Q=(qij)n×n≥0，D=-(P+Q)是非奇异M-矩阵.在初值条件u(t0+s)∈C,s∈[-τ,0]下，设u(t)=(u1(t),…,un(t))∈C[[t0,∞),Rn]满足下面不等式条件:

D+u(t)≤Pu(t)+Q[u(t)]τ+J,t≥t0. (2)

如果初值条件满足

u(t)≤kze-λ(t-t0)-(P+Q)-1J,

t∈[t0-τ,t0],

(3)

其中，k≥0,z=(z1,z2,…,zn)T>0，正数λ由下面不等式决定

[λI+P+Qeλτ]z<0,

(4)

那么

u(t)≤kze-λ(t-t0)-(P+Q)-1J,t≥t0. (5)

为了获得所需结果，需要下列条件：

(A1) 对∀j∈N和x∈Rn，都有|fj(x)|≤αj|x|和|gj(x)|≤βj|x|,

(A2) 对∀i∈N和s1,s2∈R(s1≠s2)，(ci(s1)-ci(s2))/(s1-s2)≥γi>0,

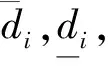
(A4) 存在非负常数νij和μij，使得对∀u,v∈Rn有

trace[(σi(u,v))(σi(u,v))T]≤

(A5) 存在正数λ和一向量z满足

其中

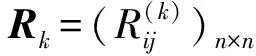
k=1,2,…;

(6)

(A7)

k=1,2,…,

(7)

其中，δk≥1和vk≥1满足

k=1,2,…,

(8)

其中

(9)

2 主要结果

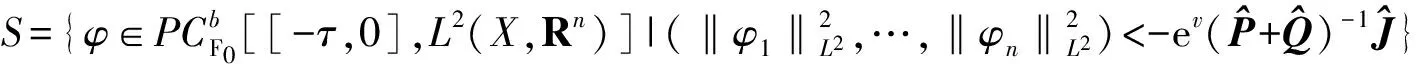
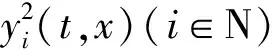
由边界条件和格林公式得

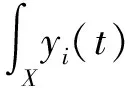
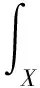
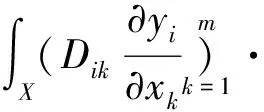
由条件(A1)～(A5)和不等式|ab|≤a2/2+b2/2得

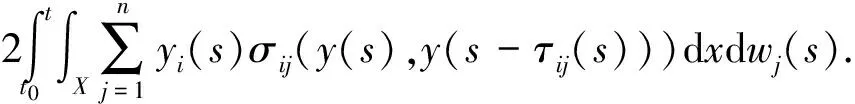
那么可得

(11)

对充分小的△t>0可得

(12)

由((11))和(12)有

(13)

从上式可得

即

(14)

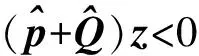
(15)

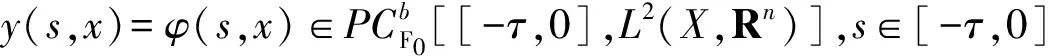
t∈[-τ,0],i∈N，

(16)

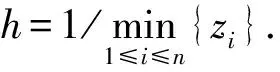
那么由(14)～(16)式和引理1.2可得

0≤t

(17)

假设对所有的m=1,2,…,k,下列不等式成立

v0v1…vm-1ρi,t∈[tm-1,tm),i∈N,

(18)

其中δ0=v0=1.由(A6)～(A7)和(18)式和引理1.1可得

i∈N.

(19)

由(18)～(19)式和δk,vk≥1可得

v0v1…vk-1vkρi,t∈[tk-τ,tk],i∈N. (20)

另一方面，由(14)式和vk≥1可得

(21)

由(15),(20)～(21)式和引理1.2可得

v0v1…vk-1vkρi,t∈[tk,tk+1),i∈N.

由递推法可得

i∈N,t∈[tk,tk+1),k=0,1,2….

所以，定理2.1证明完毕.

3 例子

例3.1考虑下面模型

条件(A5)的参数如下:

取z=(1,1)和λ=0.1可得

设α1k=α2k=e0.2k/3,β1k+β2k=2e0.2k/3和tk-tk-1=8k,那么

显然，定理2.1的所有条件成立.故

是(22)式的吸引集.

[1] Cohen M, Grossberg S. Absolute stability of global pattern formulation and parallel memory storage by competitive neural net networks[J]. IEEE Trans Syst Man Cybernet,1983,13:815-826.

[2] 龙述君. 具有分布时滞的脉冲Cohen-Grossberg神经网络的指数稳定性[J]. 四川师范大学学报:自然科学版,2009,32(1):68-71.

[3] 龙述君,张永新,向丽. 具有混合时滞的随机细胞神经网络的稳定性分析[J]. 四川师范大学学报:自然科学版,2012,35(6):796-801.

[4] Cao J, Liang J. Boundedness and stability for Cohen-Grossberg neural network with time-varying delays[J]. J Math Anal Appl,2004,296:665-685.

[5] Lu K, Xu D, Yang Z. Global attraction and stability for Cohen-Grossberg neural networks with delays[J]. Neural Networks,2006,19:1538-1549.

[6] Song Q, Cao J. Stability analysis of Cohen-Grossberg neural network with both time-varying and continuously distributed delays[J]. J Comput Appl Math,2006,197:188-203.

[7] Yuan K, Cao J. An analysis of global asymptotic stability of delayed Cohen-Grossberg neural networks via nonsmooth analysis[J]. IEEE Trans Circ Syst,2005,52I(9):1854-1861.

[8] Wan L, Zhou Q. Exponential stability of stochastic reaction-diffusion Cohen-Grossberg neural networks with delays[J]. Appl Math Comput,2008,206:818-824.

[9] Wang D S, Huang L H. Periodicity and global exponential stability of generalized Cohen-Grossberg neural networks with discontinuous activations and mixed delays[J]. Neural Networks,2014,51:80-95.

[10] Mathiyalagan K, Park J H, Sakthivel R, et al. Delay fractioning approach to robust exponential stability of fuzzy Cohen-Grossberg neural networks[J]. Appl Math Comput,2014,230:451-463.

[11] Ke Y Q, Miao C F. Stability analysis of inertial Cohen-Grossberg-type neural networks with time delays[J]. Neurocomputing,2013,117:196-205.

[12] Wan L, Zhou Q H. Asymptotic behaviors of stochastic Cohen-Grossberg neural networks with mixed time-delays[J]. Appl Math Comput,2013,225:541-549.

[13] Wang J L, Wu H N, Guo L. Stability analysis of reaction-diffusion Cohen-Grossberg neural networks under impulsive control[J]. Neurocomputing,2013,106:21-30.

[14] Zhao H Y. Invariant set and attractor of nonautonomous functional differential systems[J]. J Math Anal Appl,2003,282:437-443.

[15] Xu L G, Xu D Y.p-attracting andp-invariant sets for a class of impulsive stochastic functional differential equations[J]. Comput Math Appl,2009,57:54-61.

[16] Huang Y M, Zhu W, Xu D Y. Invariant and attracting set of fuzzy cellular neural networks with variable delays[J]. Appl Math Lett,2009:478-483.

[17] Liao X X, Luo Q, Zeng Z G, et al. Global exponential stability in Lagrange sense for recurrent neural networks with time delays[J]. Nonlinear Anal:RWA,2008,9:1535-1557.

[18] Berberian S K. Fundamentals of Real Analysis[M]. New York:Springer-Verlag,1999.