耐压加筋圆环形结构的强度特征分析

邹 广，杜青海,张博文

(中国船舶科学研究中心，江苏 无锡 214082)

0 引 言

当今世界各国经济的发展越来越受制于陆上资源的枯竭，因而深海资源的探测与开发利用逐渐成为各国角逐的焦点，这给新型水下平台及航行体的研制提出了更高要求。传统水下平台及航行体常采用圆柱型或球型耐压壳体，这种结构形式虽然具有良好的水动力性能，但是不利于平台的总体布置及人员的贯通。随着人们对深海工程装备的功能提出越来越高的要求，水下平台及航行体的结构形状也面临发展和创新。

近年来，英国学者Carl T.F.Ross[1-2]在设计水下导弹发射基地和水下空间站时，建议在水下工程中采用以环壳为主要结构形式的耐压结构方案(见图1)，即将油田用特种钢HY80钢弯成圆环，再把各个圆环纵向焊接在一起，构成耐压壳体。通过圆环壳特有结构形式实现水下平台及水下航行体特有的功能，充分解决了空间总体布置及人员贯通等问题，从而为发展深海装备及资源探索与开发利用提供了新的选择。

图1 水下空间站概念方案Fig.1 A concept draft of an underwater space station

事实上，环壳结构作为基本结构原件在容器管道工业、核工业、电力行业、海洋工程、航天航空工程等工业领域应用十分广泛，例如波纹管、托克马克装置、环形储油罐等。但需要注意的是，由于环壳壳体结构形式复杂，壳体曲面曲率的变化造就了理论求解的困难。针对不含加强肋骨型材的纯圆环壳结构模型，众多学者进行研究，取得了一些成果。对于受轴对称载荷的圆环壳，钱伟长和郑思梁[3]得到了一般解。对于承受任意非对称载荷的圆环壳，陈山林[4]采用Fourier级数法求解得到了比较完整且简单的解析解，张若京[5]选择广义Airy函数作为展开函数得到了全部4个基解和1个特解的完全渐近展开式。

对于加筋圆环壳结构模型，杜青海等[6-7]采用数值方法对水下耐压圆环结构和传统圆柱结构进行了初步对比研究，揭示了环壳结构较传统柱壳结构在水下运载器船体结构上的优势；同时结合弹塑性理论和船体结构加工制造等问题对深海外压作用下加筋圆环壳结构的非线性性能进行了深入探索研究。本文在此工作及简化理论求解[8]基础上，对应用深海工程主体结构的加筋圆环壳结构强度特征进行分析和工程应用研究，为新型圆环形结构的建造与工程应用奠定技术理论基础。

1 计算模型及其“等效柱壳”

由于传统圆柱壳几何形状和建造工艺相对简单，加筋圆柱壳强度及稳定性问题的理论和工程设计方法均已成熟。因此为了寻求加筋圆环壳的结构特性及其工程设计方法，可建立相应的类比准则对加筋圆环壳相对柱壳进行对比研究和规律探索。

结合水下工程柱形舱段结构设计优化主要技术参数特点，对加筋圆环壳类似于柱壳可比舱段参数的同比准则[6-7]如下：

截面横截面圆的半径a相同；

舱段横截面圆圆心构成轴线长度L相同。

2 圆环壳结构特性分析

如图2所示，设圆环壳两向主曲率坐标分别为θ，φ，其中θ为壳体上某点所在经线面与基准经线面的夹角，φ为经过壳体上某点截面圆中面的垂线与旋转轴的夹角。根据薄膜理论，可以得到均匀外压力作用下圆环壳结构的主应力以及截面圆切向和法向的位移

图2 加筋圆环壳计算模型及其“等效柱壳”Fig.2 A model of ring-stiffened circular toroidal shell and its equivalent cylindrical shell

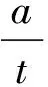
η=σφ/σθ。

(3)

图3给出了圆环壳应力比值系数随其相对弯曲半径R/a及截面圆上位置参数φ的变化规律。可以看出，圆环壳应力比值系数最大值位于内圈处(图4所示DD′位置)，最小值位于外圈处(图4所示BB′位置)。当R/a=1.25时，内圈处的应力比值系数η=6，外圈处的应力比值系数η=1.556，两者大约相差4倍。因此，当相对弯曲半径较小时，圆环壳截面圆上各点的周向应力相差较大。而圆柱壳周向一圈上各点的周向应力相同，应力比值系数η=2。截面圆上各点处的周向应力相差较大，这是圆环壳区别于其“等效柱壳”的一个很重要的结构特性。

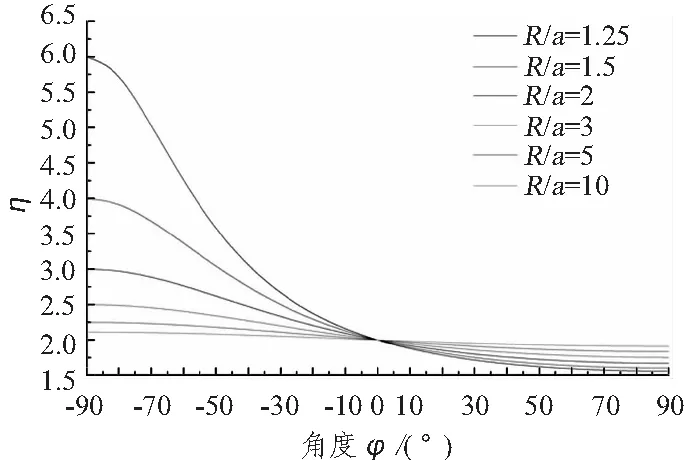
图3 圆环壳周向应力集中系数变化曲线Fig.3 Longitudinal stress concentration factors of a circular toroidal shell

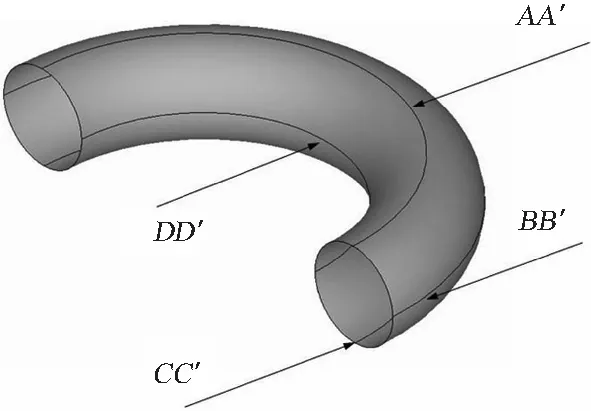
图4 圆环壳典型位置Fig.4 Typical positions of a circular toroidal shell

从图3中还可以看出，圆环壳顶圈处(图4所示AA′或CC′位置)的应力比值系数与其相对弯曲半径R/a无关，并且应力比值系数η=2，与其“等效柱壳”的应力特征相同。因此，在进行对比分析时，应该依据顶圈位置的弧长确定“等效柱壳”的舱段长度，这样才能够保证力学等效的准确。随着对弯曲半径逐渐增大，圆环壳截面圆上各点的周向应力逐渐趋近于其“等效柱壳”的周向应力。

在圆环壳顶圈处，φ=0或φ=π，根据位移表达式，lntan(φ/2)→∞，从而截面圆切向的位移u→∞，这说明薄膜应力状态下圆环壳变形不协调。因此，在圆环壳的顶圈位置处必然存在着弯矩，使得其不满足薄膜理论假设。即使在均匀外压力作用下也存在着弯矩，这是圆环壳区别于其他一般旋转壳的地方。圆环壳的这一结构特性由其壳体特殊的曲面形状引起，顶圈两侧壳体曲面高斯曲率正负反号。

3 加筋圆环壳结构强度理论解

当圆环壳受均匀压力作用时，由于结构和载荷都对称于旋转轴，在失稳之前壳的变形也必然对称于旋转轴。肋骨的存在约束了壳的压缩变形，壳体受到肋骨的反作用力而在环向产生弯曲，使得加筋圆环壳的变形不再轴对称。但是由于加筋圆环壳的结构和载荷对称于每一肋骨断面，壳的变形也必然对称于每一肋骨断面，因而只需要研究其中的一个肋骨间距。这样使得加筋圆环壳的强度问题可以按从圆环壳上截取的单位宽度的曲梁带模型来研究。求解过程具体参考文献[8]，可以得到加筋圆环壳典型位置应力表达式。

跨度中点处环向应力及周向应力：

跨度端部环向应力及周向应力：

肋骨应力：

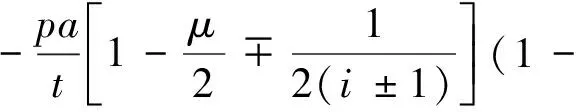
(6)

最大挠度：

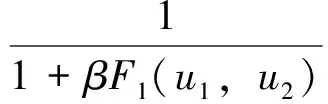
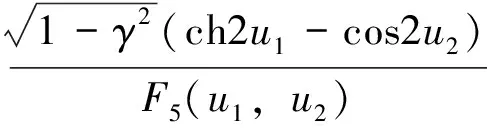
F3(u1,u2)=

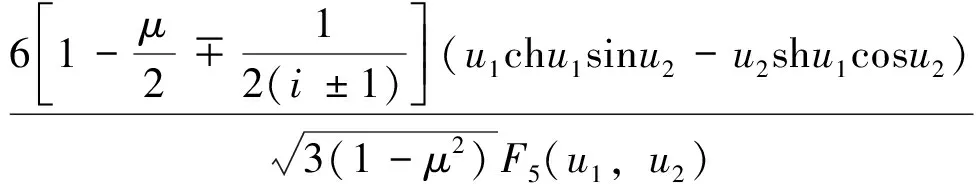
F4(u1,u2)=

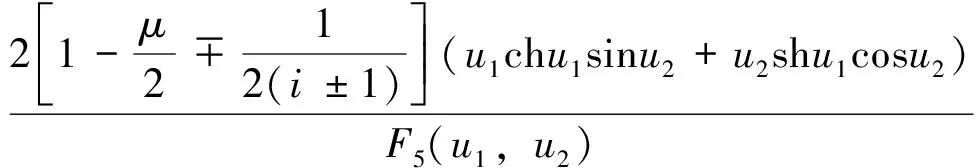
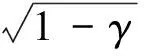
4 加筋圆环壳结构特性分析

采用型材肋骨加强的圆环壳结构虽然其稳定性大大加强，但是由于肋骨约束了壳的轴对称变形，使得局部强度可能有所减弱，因此加筋圆环壳的强度问题值得关注。根据上节加筋圆环壳结构强度理论解，可以分析计算加筋圆环壳典型位置处的应力及变形。为使下面的讨论不失一般广泛的意义，定义应力集中系数

根据加筋圆环壳结构强度理论解可知，外圈和内圈处的环向应力集中系数kc、周向应力集中系数kt、肋骨应力集中系数kf仅与4个无量纲参数u，β，γ，R/a有关。本节针对具体参数给出了环向轴力及相对弯曲半径对加筋圆环壳结构强度及变形的影响曲线，从而揭示了梁柱效应对弯曲的影响以及圆环壳内、外圈结构性能的差异。

4.1 环向轴力对加筋圆环壳应力的影响

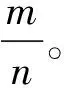
从式(9)可以看出，如果没有环向压缩力，即T1=0， 则m=0，γ=0， 圆环壳曲梁带为简单弯曲。当载荷p为均匀外压力时，环向轴力为压缩力，则γ>0。 反之，当载荷p为均匀内压力时，环向轴力为拉伸力，则γ<0。 因而参数γ实际上反映了环向轴力T1对壳体弯曲的影响，或称为梁柱效应。对于圆环壳来讲环向轴力T1永远存在，即T1≠0， 因而梁柱效应总存在。

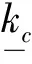
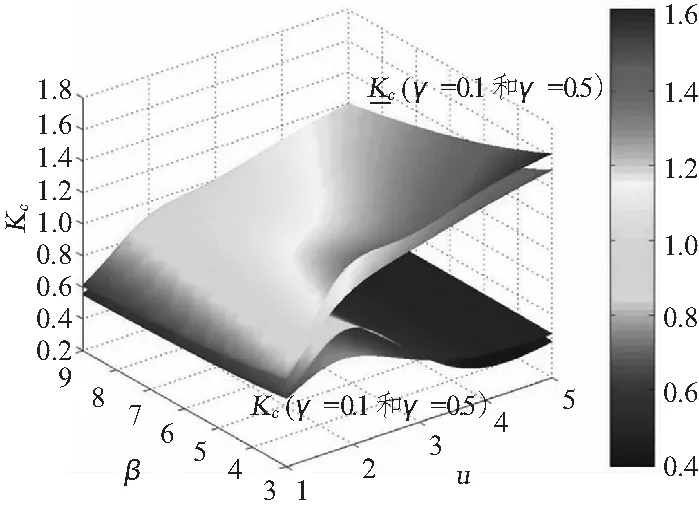
图5 环向应力集中系数kc变化云图Fig.5 Latitudinal stress concentration factors kc

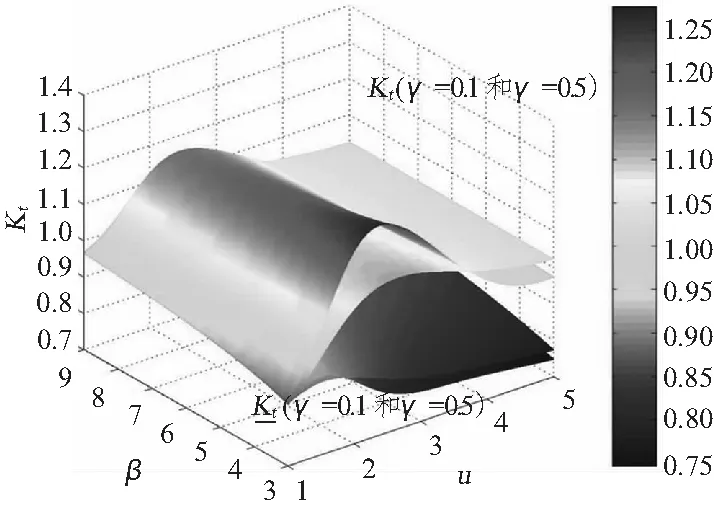
图6 周向应力集中系数kt变化云图Fig.6 Longitudinal stress concentration factors kt

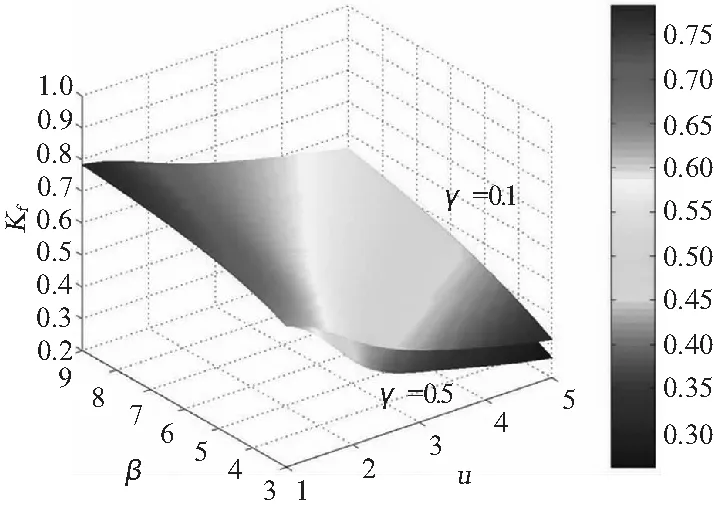
图7 肋骨应力集中系数kf变化云图Fig.7 Stress concentration factors kf of the ribs

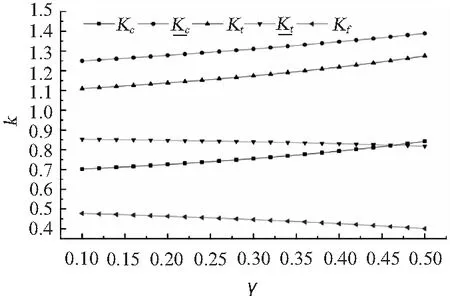
图8 内圈应力集中系数k变化曲线(R/a=20,u=2.4,β=3)Fig.8 Stress concentration factors k of the internal parts

总体来讲，参数γ对应力的影响微小。仅当1.5

4.2 外圈和内圈结构特性比较分析

圆环壳由于其特殊的结构形式，既存在正高斯曲率面，又存在负高斯曲率面，造成其弯曲方程在顶圈处具有奇异性，顶圈两侧方程的性质完全不同。对于均匀外压力作用下加筋圆环壳的强度问题，当采用弹性基础曲梁模型求解时，外圈处环向压缩力T1与外载荷p方向相反，内圈处环向压缩力T1与外载荷p方向相同，从而使得这2个典型位置处的弯曲方程有所不同，应力及位移表达式也必然不同。为了分析对比加筋圆环壳内圈和外圈处结构特性的差异，将两处应力集中系数之比定义为参数

表1参数换算关系

Tab.1 Relations of the parameters

等效柱壳圆环壳外圈圆环壳内圈u(1+1/i)u(1-1/i)uβ(1+1/i)β(1-1/i)βγγγ

从图9中很容易看出：1)加筋圆环壳内、外圈应力集中系数的比值λ主要受参数R/a的影响，随着R/a的不断增大，λ逐渐趋近于1，即内圈与外圈之间的差别消失；2)加筋圆环壳内、外圈应力集中系数的比值λ随参数γ变化很小；3)内、外圈应力集中系数的比值λ随着参数u的增大而增大；当1

5 结 语

本文首先运用弹性薄壳理论，对均匀压力作用下圆环壳进行线弹性求解和强度特征参数化研究，从本质上揭示圆环壳理论求解的难点所在。同时在简化理论解的基础上，对加筋圆环壳结构强度特征参数进行比较分析和应用研究，并给出典型位置关键点上的应力随其结构参数的变化曲线，为新型耐压环形结构的设计、建造与应用提供科学依据和参考。通过本文的研究，可以得出以下结论：

1)当相对弯曲半径R/a较小时，截面圆上各点处的周向应力相差较大，从内圈处到外圈处应力水平逐渐降低。即使在均匀压力作用下，圆环壳顶部(φ=0或φ=π)也存在着弯矩，故环壳结构不适合用无矩理论求解。

图9 内、外圈应力集中系数的比值λ变化曲线Fig.9 Stress concentration factor ratios of the internal parts to the external parts

2)环向轴力对加筋圆环壳结构的弯曲影响较小，表现为参数γ对结构强度特征影响较小。当采用弹性基础曲梁模型求解加筋圆环壳结构强度问题时，弹性基础曲梁的刚度相当大，故梁柱效应对加筋圆环壳结构的弯曲影响很小。

3)当R/a较小时，加筋圆环壳外圈处和内圈处结构强度特征差异显著。采用弹性基础曲梁模型求解时外圈处环向压缩力T1与外载荷p方向相反，而内圈处环向压缩力T1与外载荷p方向相同，两处弯曲方程不同，从而强度特征不同。

[1] CARL T F.ROSS.A conceptual design of an underwater mis-sile launcher[J].Ocean Engineering,2005(32):85-99.

[2] CARL T F.ROSS.A conceptual design of an under-water vehicle[J].Ocean Engineering,2006(33):2087-2104.

[3] 钱伟长,郑思梁.轴对称圆环壳的一般解[J].应用数学和力学,1980,1(3):287-299.

QIAN Wei-chang,ZHENG Si-liang.General solution to the axisymmertric circular toroidal shell[J].Applied Mathe-matics and Mechanics,1980,1(3):287-299.

[4] 陈山林.圆环壳在一般载荷下的轴对称问题[J].应用数学和力学,1986,7(5):425-434.

CHEN Shan-lin.Axisymmertric problem of the circular toroidal shell under general load[J].Applied Mathematics and Mechanics,1986,7(5):425-434.

[5] 张若京,张维.承受非对称载荷圆环壳的完全渐近解[J].中国科学，1995,25(6):614-619.

ZHANG Ruo-jing,ZHANG Wei.Complete asympototical solution for the circular toroidal shell under non-axisymmetric loadJ].China Science,1995,25(6):614-619.

[6] DU Qing-hai,WAN Zheng-quan,CUI Wei-cheng.A study on structural characteristics of the ring-stiffened circular toroidal shells[C].2ndInternational Conference on Marine Structures-Analysis and Design of Marine Structures, Lisbon,2009.

[7] DU Qing-hai,CUI Wei-cheng,WAN Zheng-quan.Nonlinear finite element analysis of a toroidal shell with ring-stiffened ribs[C].Proceedings of the ASME 2010 29thInternational Conference on Ocean,Offshore and Arctic Engineering,Shanghai,2010.

[8] 邹广,彭兴宁,杜青海.加筋圆环壳的理论求解及性能研究[J].船舶力学，2012,16(1):83-92.

ZOU Guang,PENG Xing-ning,DU Qing-hai.Theoretical solution and performance study of ring-stiffened circular toroidal shell[J].Ship Mechanics,2012,16(1):83-92.