利用面元法计算潜艇在水底引起的压力分布

黎 昆，张志宏，顾建农，缪 涛

(1.91388部队,广东 湛江 524022； 2.海军工程大学 理学院，湖北 武汉 430033)

0 引 言

指挥台围壳作为潜艇上的最大附体，对潜艇水动力性能和隐蔽性有显著影响。美国的Tailor船池以SUBOFF模型作为标准模型进行系统的水动力与流场的测量实验工作，提供包括速度、压力和阻力等大量的水动力和流场数据，为计算流体力学研究者提供了一个用来验证数值计算程序的交流平台[1-2]。

吴宝山[3]以SUBOFF模型为研究对象，分析研究潜艇近海底运动时的水动力特性。洪祥武[4]在理论上研究了潜艇指挥台围壳外流场的压力分布特性，提出利用围壳流场负压区负压特性布置排气口位置以降低排气背压的最佳方案。刘祖源[5]对指挥台围壳处于不同相对位置的潜艇若干水动力特性分别进行建模计算。王志博[6]通过数值计算分析了艇体围壳绕流的演化过程，比较了不同围壳外形对尾部流场结构的影响。吴方良[7]通过数值计算研究指挥台围壳高度和在潜艇上的分布位置对其后方流场和阻力的影响，分析了潜艇指挥台围壳对潜艇水动力性能的影响。杜波[8]运用计算流体力学数值计算手段对指挥台围壳的型线进行数值优化研究。邱辽原[9]采用有限体积法计算了潜艇指挥台围壳与尾翼表面不同高度处的压力系数分布。

尽管不少学者在指挥台围壳与艇体匹配的流场性能方面已经做大量研究，但针对潜艇大深度航行时在水底引起的压力变化研究却很少。本文利用某优化后的水滴形潜艇主体，按照恰当比例配置指挥台位置，假定潜艇深潜于水中定常运动且距离自由液面较远(可忽略兴波影响)，进而利用Hess-Smith方法(面元法)，将面源分布于潜艇外表面上，采用镜像法满足水底和自由表面固壁条件。通过编制计算程序，求解水下航行潜艇在水底引起的压力分布，并将计算结果与潜艇模型实验结果进行比较，总结得到大潜深条件下潜艇水压场的分布特征。

1 基本方程

设潜艇深潜于理想不可压无旋运动流体中，航速为v∞， 长为L， 距离水底高度为h， 距离水面高度为h1。 假定潜深较大，水面兴波影响可忽略不计，自由表面视为固壁处理。坐标系原点取在潜艇纵轴轴线中点上，x轴指向潜艇尾部，z轴垂直向上，符合右手直角坐标系规则，如图1所示。

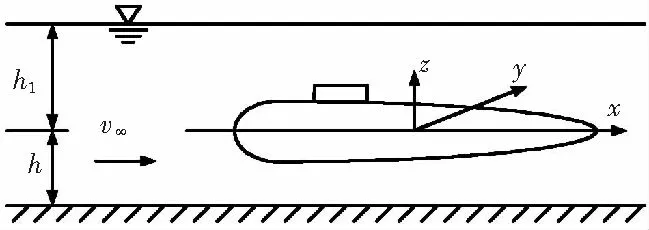
图1 潜艇绕流示意图Fig.1 Sketch map of flow around submarine

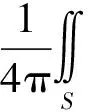
式中：ni为物面的单位外法线方向；q为物面上连续分布的源点；r(qi,q)为源点q至控制点qi的距离；S为潜艇外表面，未知源强分布密度σ通过物面条件确定。

2 积分方程的离散

在潜艇外表面S上划分网格，沿艇长方向和垂直艇长方向将S分割成N个四边形小面元Sj，调节面元Sj的4个角点形成平面面元，在每个面元上布置源强密度为σj的面源，当面元足够小时可视σj为常数。

利用物面条件：(v∞+▽φ)·ni=0，再根据式(1)，则有：

(2)

在每个面元的控制点上均可由式(2)生成一个方程，共形成N个方程，则可得到线性代数方程组：

(3)

式中：Bi=-4πv∞·ni；

式(3)是一个N阶线性代数方程组，系数矩阵满秩且对角线占优(为2π)。

3 编程计算

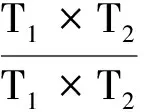
用平面面元Dj代替曲面面元Sj。 在平面面元上建立以形心C为原点的局部坐标系Cξηζ， 对应的坐标轴单位矢量为e1，e2，e3。 则影响系数可写为

cj(qi)=cj1e1+cj2e2+cj3e3=

根据文献[10]中的条带积分法，可得cj1、cj2、cj3用各角点坐标表示的多项式。为满足水面和水底固壁条件，将面元Sj以水面为镜面作镜像得其映像Sj 1，以水底为镜面作镜像得其映像Sj 2，再以水底为镜面作Sj 1的镜像其映像Sj 3，以水面为镜面作Sj 2的镜像其映像Sj 4， 依次类推分别以水面和水底为镜面共作8次镜像，经计算结果验证其误差小于1.0×10-6。 分别计算每个面元在总体坐标系和局部坐标系中的控制点和4个角点的坐标值，求出面元的单位外法线ni和影响系数cj(qi)，利用赛德尔迭代法求解代数方程组式(3)，即可求出源强分布密度σj。在此基础上，流场p点处的速度和压力系数为

(5)

4 计算结果与实验结果比较

潜艇模型长度L=2.4 m，带有指挥台围壳及尾翼等部件。模型实验在武汉理工大学拖曳船池中进行，利用水底压力测量系统对艇模在水中航行时引起的水底压力变化进行实验测量。水池长108 m，宽10.8 m，水深2 m。压力传感器距潜艇艇体一侧布置于水底，横距位置为y=0，0.25L和0.5L，根据对称性垂直于航迹一侧布置，1次测量可得船模多条水压场通过特性曲线。

本文计算了主艇体(不带围壳)和潜艇在距水底深度分别为h=0.1L，0.2L，0.3L，0.4L，0.5L共5个水深的压力分布，并与实验结果进行比较分析，可知：

1)当h=0.1L～0.5L时，计算结果表明，主艇体和潜艇的水压场曲线几乎重合，说明在此水深范围指挥台围壳对潜艇在水底引起的压力变化影响很小，可以不予考虑，如图2～图5所示。当h=0.1L～0.3L时，计算结果与实验结果基本吻合，如图2～图4所示，而当h>0.3L时，计算结果与实验结果差别增大，如图5所示。

2)当水深较小时(h=0.1L)，潜艇水压场纵向通过特性曲线负压区呈W型分布，从正压峰值到负压峰值或从负压峰值到正压峰值的压力变化曲线很陡，如图2所示。潜艇水压场纵向通过特性曲线左右正压峰值明显不对称，艇首正压峰值大，艇尾正压峰值小，这与潜艇横截面积前后不对称且离水底较近有关。

图2 潜艇水压场纵向通过曲线比较(h=0.1L)Fig.2 Comparison between the longitudinal curves of submarine hydrodynamic pressure field(h=0.1L)

图3 潜艇水压场纵向通过曲线比较(h=0.2L)Fig.3 Comparison between the longitudinal curves of submarine hydrodynamic pressure field(h=0.2L)

3)当水深增大时(h=0.2L～0.3L)，水压场纵向通过特性曲线负压区由W型转呈U型分布，潜艇水压场纵向通过特性曲线左右正压峰值稍不对称，如图3和图4所示。当水深进一步增大时(h>0.3L)，潜艇水压场纵向通过特性曲线负压区呈V型分布，且左右形状基本对称，如图5所示。说明当潜艇距离水底较远时，潜艇横截面面积分布前后不对称导致的远场水底压力变化差别较小，潜艇远场水压场主要取决于长度、最大直径、排水量等主尺度参数。

图4 潜艇水压场纵向通过曲线比较(h=0.3L)Fig.4 Comparison between the longitudinal curves of submarine hydrodynamic pressure field(h=0.3L)

图5 潜艇水压场纵向通过曲线比较(h=0.5L)Fig.5 Comparison between the longitudinal curves of submarine hydrodynamic pressure field(h=0.5L)

5 结 语

基于船舶水动力学势流理论，采用Hess-Smith方法对潜艇表面进行网格划分，将源汇分布于每个面元上，编制程序计算出面元强度，在此基础上计算潜艇在不同水深时的压力场分布，通过与实验结果比较验证程序的可靠性。Hess-Smith方法的优越性在于能反映实际艇型对潜艇水压场的影响。根据计算和实验结果，分析潜艇水压场的分布特征和指挥台围壳对潜艇水压场的影响特性。利用潜艇水压场作为水中目标的物理场特性，可以为水中兵器的探测和利用提供理论依据。

[1] BULL P,WATSON S.The scaling of high reynolds number viscous flow predictions for appended submarine geometries[C]//Proceedings of 22ndSymposium on Naval Hydrod-ynamics.Washington:[s.n.],1998.

[2] BENSOW R E,et al.Large eddy simulation of the viscous flow around submarine hulls[C]//25thSymposium on Naval Hydrodynamics.St John′s,Newfoundland and Labr-ador,2004.

[3] WU Bao-shan,XING Fu,KUANG Xiao-feng,et al.Inve-stigation of hydrodynamic characteristics of submarine moving close to the sea bottom with CFD methods[J].Journal of Ship Mechanics,2005,9(3):19-28.

[4] 洪祥武，段远才，孙亦兵,等.潜艇指挥台围壳流场压力特性及其应用的研究[J].水动力学研究与进展,1993,8(4):448-453.

HONG Xiang-wu,DUAN Yuan-cai,Sun Yi-bing,et al.Study on pressure distribution characteristics of flow field outside submarine superstructure hull and its new application[J].Journal of Hydrodynamics,1993,8(4):448-453.

[5] 刘祖源，林小平，周朝晖.潜艇指挥台位置对水动力的影响研究[J].海军工程大学学报,2006,18(16):30-33.

LIU Zu-yuan,LIN Xiao-ping,ZHOU Zhao-hui.Study on relative position of submarine sail zone[J].Journal of Naval University of Engineering, 2006,18(16):30-33.

[6] 王志博，姚惠之，张楠.指挥台围壳对潜艇尾流影响的计算研究[J].船舶力学,2009,13(2):196-202.

WANG Zhi-bo,YAO Hui-zhi,ZHANG Nan.Calculation and analysis of the effects of sail form on submarine wake[J].Journal of Ship Mechanics,2009,13(2):196-202.

[7] 吴方良，吴晓光，马运义.潜艇指挥台围壳对阻力和伴流场影响数值研究[J].海洋工程,2009,27(3):91-99.

WU Fang-liang,WU Xiao-guang,MA Yun-yi.The effect of submarine sail on the resistance and wake field[J].The Ocean Engineering,2009,27(3):91-99.

[8] 杜波，黄建伟，陈源.潜艇指挥室围壳顶部型线构型[J].船海工程,2007,36(2):108-110.

DU Bo,HUANG Jian-wei,CHEN Yuan.Optimal design of the top form of submarine sail[J].Ship & Ocean Engineering,2007,36(2):108-110.

[9] QIU Liao-yuan,SHI Zhong-kun,HOU Guo-xiang,et al.Validation of numerical simulation of the flow over submarine geometries with full appendages[J].Journal of Ship Mechanics,2007,11(3):341-350.

[10] HESS J L,SMITH A M O.Calculation of non-lifting pot-ential flow about arbitrary three-dimensional bodies[R].Virginia:Armed Services Technical Information Agency,1962.