解题架桥 促进思维 培养能力

☉江苏省扬州市邗江中学 倪富春

解题架桥 促进思维 培养能力

☉江苏省扬州市邗江中学 倪富春

“注重提高学生的数学思维能力”确定为高中新课程的基本理念之一，因此，培养学生的数学思维能力也就显得十分重要.在教学中如何实现这个理念，是一线教师一直追寻的目标.数学问题是数学的心脏，所以，在我们大量的数学问题教学中，要随时善于利用一些解决问题的常用数学思想方法来培养学生的思维能力.下面举例说明.

一、消除思维定势，培养学生数学思维的灵活性

思维定势是指影响或决定同类后继心理活动的趋势或形成心理活动的准备状态，即人们用一种固定的思维习惯去考虑问题，表现为人们思维的一种趋向性和专注性.虽然思维定势有助于学生运用学过的知识和积累的经验去解决问题，但它也表现出思维的刻板和惰性，妨碍学生灵活性和创造性思维的发展.

分析：欲通过化简方程，与常见曲线方程对比，得出曲线形状；但运算量大，结果也并不直观，显然，这种做法不可取.本题中，学生没有注意到方程的特点以及蕴含的几何含义，并忽视了圆锥曲线的统一定义.这暴露出了学生思维定势，简单僵化，缺乏灵活性.

由圆锥曲线的统一定义知，平面上动点到一定点与到一定直线的距离之比是一个常数，当这一常数大于1时，动点轨迹为双曲线.

点评：思维的灵活性即善于全面地、科学地考察问题、分析问题，从各种事物的各种联系中去认识事物.思维比较灵活的学生，不仅能够把握住事物的全体，抓住事物的基本特征，而且也不会忽视重要的细节问题.

二、注重一题多解，培养学生数学思维的广阔性

对于教学中的例题，引导学生一题多解，挖掘题目本身蕴含的教学价值，从而培养学生思维的广阔性.

例2“若x，y为正实数，且满足：xy-2x-y=1，求2x+y的最小值.”

这两种方法有异曲同工之妙，都是利用基本不等式，可以转化成2x+y，也可以转化成xy，还有没有其他的方法呢？在学生的热烈讨论之后，又得出了几种解法：

这样一道平常的题目就有四种解法，事实上学生的想法和思路是很多的，我们平时上课不能压抑学生的想法，应该多花点时间让学生自主思考，自主讨论，各抒己见.通过这样的一题多解，一方面，学生不仅可以看到知识之间的联系和沟通，他们也将学会如何思考问题，将陌生的问题转化成熟悉的问题，充分调动学生所学过的知识和方法，这也是我们常说的“举一反三、触类旁通”，对培养学生思维的广阔性有很大的帮助.

三、关注隐含条件，培养学生数学思维的严密性

点评：思维的严密性表现为思维过程服从于严格的逻辑规则，考察问题时严格、准确，进行运算和推理精确无误.

在三角函数的学习中，学生经常会忽视三角函数的有界性、已知条件中的隐含条件等问题.另外在对参数的分类讨论、根与系数关系的应用（需要考虑判别式）、求函数的极值（需要检验左右两侧导数符号）等问题中，一些学生也往往会出现疏忽遗漏.这要求我们在平时的教学中，充分暴露学生的错误表现、思维障碍，引导学生关注隐含条件，发现错误，自主评价，并辅之适当的针对训练，如此才使学生既能钻的进去，又能跳的出来.从而，避免丢三落四、疏忽遗漏，达到培养学生思维严密性的目的.

四、加强解题后的反思，培养学生数学思维的批判性

例4 已知直线l过不同的两点A（cosθ，sin2θ），B（0，1），求直线l的倾斜角α的取值范围.：当生1说出答案时，一些同学便认为正确，思维被生1同化；当生2开始质疑时，又有很多同学开始赞赏，思维又被生2同化.这道题虽不难，但却隐藏着“陷阱”，很多学生出现了失误.这些同学在解题后没有能够及时反思，这暴露出他们思维缺乏批判性.

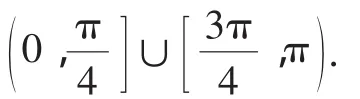
点评：批判性思维指的是对别人的观点或自己原有观点进行反思，提出质疑并有所创新的思维，其核心在于反思.为了培养学生这种批判性思维，除了建立民主平等的师生关系、鼓励学生主动反思和质疑外，还要求教师在习题教学中，注重对错误的辨析、溯源、纠正和反思，特别是典型的、隐蔽的错误.

总之，对于学生解题中出现的思维障碍，我们分析出现障碍的原因，结合教学实际，千方百计地引导学生突破这些障碍.在平时教学中，我们应立足课本，对课本典型的例习题进行演变、探究、引申、拓广、应用；由点到面，举一反三，解剖一例，学会一类.解题中注意数学思想方法的渗透，注重基础知识的演练，培养思维品质，发展思维能力.