反思课堂教学，给力高考复习

☉北京市第二中学通州分校 李 娜

反思课堂教学，给力高考复习

☉北京市第二中学通州分校 李 娜

高三复习特别是第一轮复习，要严格按“可接受性”的原则，把握好起点，重视概念，精选例题，逐个拆分难点，由易到难地将学生引入知识的“最近发现区”，充分挖掘书本上的例题、习题作为素材，根据学生的实际情况进行适当的变形、引申、发散来构建知识结构.如何在有限的课堂时间提升学生的数学思维能力，发展学生的应用意识和能力，使之能在有限的时间达到高质量的复习效果，笔者作了以下的一些思考.

一、反思概念教学，加深数学本质的认识

从近几年的高考数学题来看，高考将基本概念的理解放在很重要的位置上，因此，对基本概念的理解是我们高三数学教学的一个重点.那么应该如何进行概念的教学？下面从笔者听到的一节公开课谈谈个人的看法：

《数列求和》教学案例：

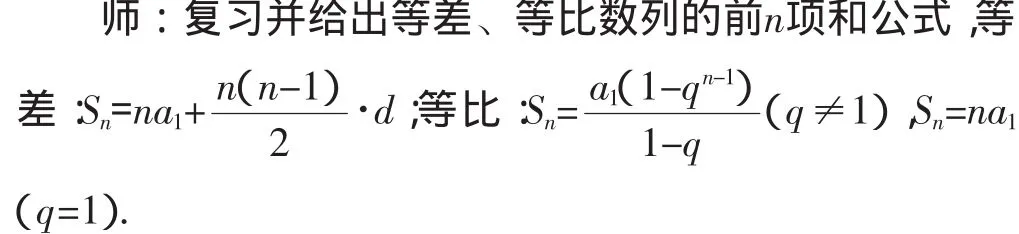
下面我们先来学习数列求和的第1种方法——分组转化求和法.请看一道题目：

生：解（略）.

师：从解题过程可看到（1）要求an就是要求出a1和q，然后把题目的条件都化为a1和q的形式即可；（2）要求数列{bn}的前n项和Tn，就要先求出通项公式bn，然后观察bn的特点，从而想到把它分组去求和.下面再做如下练习：

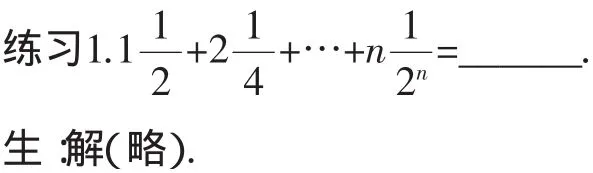
师：下面我们再来学习另外一种数列求和的方法——错位相减法.请看一道题目：

例2 已知数列 {an}的前n项和Sn且an=n·2n，则Sn= ______.

生：解（略）.

师：从解题过程可看到如果一个数列是{an·bn}，其中{an}为等差数列，{bn}为等比数列，就可以用上述的求解过程——错位相减法，下面做如下练习：

练习1.a+2a2+…+nan=______（a为常数）.

生：解（略）.

反思：上面教师教学很简洁，一开始就给出公式，接下来就是对公式的运用.这种教学方法如果用在一些数学高材生身上，效果应该很好；但这节课是在一个普通中学的普通班上的，部分同学对基本的公式都不熟悉的，还有的连数列前n项和概念是什么都不清楚的，那么这样的教学只能是对牛弹琴了.那应该怎样改进呢？对于《数列求和》这节课，应该以数列求和的概念去展开，要多出现Sn=a1+a2+…+an，在复习等差、等比数列的前n项和公式时，要具体的给出等差、等比数列的前n项和公式的推导过程，并从中体会数列求和的基本思想，这样就是回到基本概念的教学.总之，从近几年的高考对概念理解的考查和从考试中所出现的问题，足够引起我们对高三数学教学中概念教学的重视和反思，认真地做好回到基本概念教学中来.

二、反思“三基”训练，注重解题的通性通法

强调“三基”，突出“三基”，考查“三基”已成为命题的主旋律，同时各种试题清晰地告诉我们，如果在平时的“三基”训练中下足功夫，考好数学是不成问题的，如下面两道高考题就是考查基础知识的小题.

例3（2012年高考重庆理1）在等差数列{an}中，a2=1，a4=5，则{an}的前5项和S5=（ ）.

A.7 B.15 C.20 D.25

解析：因为a2=1，a4=5，所以a1+a5=a2+a4=6，所以数列的前5项和

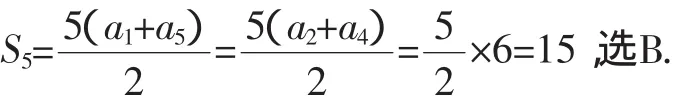
注重提炼通性通法，熟练掌握数学模式题的通用解法.从高考数学试题中可以明显看出，高考重视对基础知识、基本技能和通性通法的考查.高考命题的一个原则就是淡化特殊技巧，同学们在复习中千万不要去刻意追求一些解题的特殊技巧，尽管一些数学题目有多种解法，但这些解法中具有普遍意义的通用解法也就一两种而已，更多的是针对这个题目的专用解法，这些解法作为兴趣爱好去欣赏是可以的，但在高考复习中却不能把它当作重点.数学属于思考型的学科，在数学的学习和解题过程中理性思维起主导作用，同学们在复习时要更多地注重“一题多变”（类比、拓展、延伸）、“一题多用”（即用同一个问题做不同的事情）和“多题归一”（所谓“一”就是具有普遍意义和广泛迁移性的、“含金量”较高的那些策略性知识），更多地注重思考题目的“核心”是什么，从题目中“提炼”反映数学本质的东西.掌握好数学模式题的通用方法.

三、反思解题教学，真正落实计算能力的培养

长期以来，高中生的数学运算能力难以令人满意，“会做的做不对，会做的做不全，会做的来不及做”的现象比较普遍.除教材因素外，究其心理因素主要有：马虎浮躁，缺少责任感；焦虑失当，缺少静心思考；注意分散，缺少定律；陈述性知识和程序性知识的提取困难（表现为考试时没做出来，出了考场却恍然大悟，有时自己苦思冥想不得其解，一经同学或教师的暗示就豁然开朗；对知识的理解不透或错误，类似知识之间的区别与联系分辨不清，不能从多维问题表征中合理选择，思维单向，缺少变形意识等）.影响高中生数学运算能力的因素是多方面的，教学中除了设法优化学生思维品质，做好初高中衔接教学（如增加因式分解，一元二次方程等内容教学），还应有计划地采取相应对策，逐步提高学生的运算能力.

四、反思考题，回归课本

对教材出现的例题或习题进行适当的改造、重组形成考题是高考试题的一个特点.对课本题源的适度改造，解决它们不需要特殊的技巧，这既体现了高考的公平、公正，也对中学数学的备课、教学、辅导、批改、讲评等提供了良好的导向作用，从而让一线的教师和学生从题海中解脱出来，真正做到求真务实、抓纲务本.

例5（2013年江苏17题）在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4.设圆C的半径为1，圆心在l上.

（1）若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；

（2）若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

思路分析：（1）先联立直线方程，组成方程组，求出圆心坐标，可得圆的方程，再考虑直线斜率是否存在，确定切线的方程，利用圆心到直线的距离等于半径，求出斜率，即可求切线的方程；（2）先确定M的轨迹方程，再将问题等价转化为两圆相交或相切，利用两圆位置关系的判定方法，即可求圆心C的横坐标a的取值范围.

（解答略）

题源1：（苏教P113，例2）自点A（-1，4）作圆（x-2）2+（y-3）2=1的切线l，求切线l的方程；

相似处：都是自圆外一点作圆的切线，圆的的方程仅是圆心不同，半径相同，所求斜率值相同，解决的方法都是利用圆心到直线的距离等于半径，求出斜率；

不同处：例2点的坐标是已知的，真题点的坐标需要利用解方程组求出.

相似处：都是解决轨迹问题，而且满足的关系MA=2MO也完全相同，解决的方法都是利用等量关系，建立方程；

不同处：点A的坐标，一个是在x轴上，一个是在y轴上.

题源3：（苏教P117，感受理解5）已知圆（x-a）2+y2=1与圆x2+y2=25没有公共点，求正数a的取值范围.

（苏教P116，练习2）若圆x2+y2=m与圆x2+y2+6x-8y-11=0相交，求实数m的取值范围.

相似处：都是研究圆与圆的位置关系问题，解决的方法都是利用圆与圆的位置关系所满足的结论；

不同处：真题解决两圆相交或相切，这两道题解决圆与圆没有公共点、相交问题.

本题以重要知识直线与圆为载体，解决直线与圆、圆与圆位置关系方法为依托，立足基础，考查能力，突出对知识和方法的灵活运用，加大了分析和解决问题的思考力度，反映了新课程的理念，使被动学习者和题海战术者在应试中力不从心、难有作为.

反思：回归课本不是简单阅读课本或将课本上的例习题重做一遍，而是要认真研读课本，读出思想方法、读出拓展创新、读出对数学的欣赏、读出知识网络交接处的闪光点等，充分挖掘课本中例习题的潜在功能，比如：习题的一题多解与多提一解；类比探究与逆向探究；强化、弱化条件；一般化结论等.每年大量出现的源于课本的高考试题还不足以让我们清醒吗？

“思路决定出路”.敢问高考之路在哪里？“路”就在教材中.研究高考试题是高中教师必做的功课，潜心研究一些典型的高考试题，有助于教师从更高的视角审视教材，从整体上把握教材，让课堂教学更贴近高考.

1.李宽珍.数学教学中无处不在的“反思”［J］.中学数学（上），2013（3）.

2.张雪松.谈如何有效利用高考题［J］.中国数学教育（高中版），2010（9）.

3.徐萍.上好二轮复习课的几个着眼点——从一节数列复习课谈起［J］.中学数学（上），2013（3）.