从错误效应提高数学教学有效性
☉江苏省南通中学 唐仁霞
从错误效应提高数学教学有效性
☉江苏省南通中学 唐仁霞
高中数学在培养学生三大能力,即运算能力、逻辑思维能力、空间想象能力上有着突出的作用.但在数学学习过程中,学生往往会对某些问题产生理解上的偏差、知识整合上的缺陷,又会常常出现逻辑、理解、运算等错误,学生学习过程中的错误常常影响着他们对知识的深刻理解和知识更深层次的运用、掌握,这无疑对学生形成扎实的双基和知识之间的整合,以及更进一步的数学思想体系的建立产生了负作用.本文将从独特的错误效应利用的视角阐述,如何正确应对数学学习中出现的错误,并以这些错误为载体更好的提高数学教学的有效性.
一、问题的提出
在进入高中之后,随着高中数学更具形式化、更抽象,学生对知识的理解遇到了困难.另外因为进度较快和数学形式化的结果不能熟练理解与掌握,久而久之的困难堆积形成了思维障碍,这些障碍造成了学生学习过程中大量错误的积累,在得不到及时的解决后造成了数学科成绩低下,这种现象普遍存在于如今的高中新生之中.因此,笔者在想将这些错误成因进行归类,并利用这些常见的错误引导学生分析、理解,利用错误产生的效应对教学产生一些积极的、指导的作业,减少其学习过程类似错误的产生,提高数学教与学的有效性和学生正确看待错误产生的缘由,并帮助其提高数学的思维能力,这对教师而言是具有重要意义的一项工作.
二、错误的效应与教学有效性
1.基本功错误效应
数学的基本功,也就是传统的双基教学,一直是我国数学教学的优良传统,也是课程改革中坚持并发扬下来的东西.从高一到高二,学生一直致力于学习数学的新知,在此过程中打下坚实的基础显得尤为重要.相比初中数学,高中数学学习的特点发生了巨大的变化:新知的进度完全超乎学生的想像,使得高一新生学习数学非常疲惫;正是因为对形式化数学概念、定理等没有本质上的深刻认知,导致学生觉得数学的题型变化多端,即使能理解教材中的数学基本知识的表象也难以完全应对千变万化的试题;高中数学的运算水平陡然上升,使计算水平一般的学生止步不前等.这些都是双基缺失的具体表象,在这些困难的背后,造成学生不断在数学学习中出现错误.如何解决和利用这些错误使得学生学习更坚实、更有效呢?进而提升学生的思维能力呢?来看一个案例:
案例1(抽象函数)函数(fx)对任意的m、n∈R,都有(fm+n)=(fm)+(fn) -1,并且x>0时,恒有(fx)>1.
(1)求证:f(x)在R上是增函数;
(2)若f(3)=4,解不等式f(a2+a-5)<2.
学生错误成因:(1)对于抽象函数来说,用教师的眼光看待此类问题是大同小异的,但学生却难以理解:明明没有解析式却要分析其单调性、奇偶性,怎么使用条件中的抽象式是学生解决抽象函数的难点,这就属于学生对双基知识中——函数概念的理解还不充分;(2)在解决抽象不等式f(a2+a-5)<2的时候,学生没有利用最基本的——函数单调性脱去“f”的思想,致使问题停留在表层.
善用错误效应:抓住这样的抽象函数问题,笔者对其进行举一反三的分析:(1)对于抽象函数的单调性的证明,只能用定义.应该构造出f(x2)-f(x1)并与0比较大小.(2)将函数不等式中的抽象函数符号“f”运用单调性“去掉”是本小题的切入点;要构造出f(M)<f(N)的形式,易错点还要关注定义域的取值以及抽象函数的性质运用等.最后请学生改编此问题,请学生自己再次解决类似问题.
解析:(1)设x1<x2,所以x2-x1>0,因为当x>0时,f(x)>1,所以f(x2-x1)>1,f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1,所以f(x2)-f(x1)=f(x2-x1)-1>0圯f(x1)<f(x2),所以f(x)在R上为增函数.
(2)因为m,n∈R,不妨设m=n=1,所以f(1+1)=f(1)+
f(1)-1圯f(2)=2f(1)-1,f(3)=4圯f(2+1)=4圯f(2)+f(1)-1=4圯3f(1)-2=4,所以f(1)=2,所以f(a2+a-5)<2=f(1),因为f(x)在R上为增函数,所以a2+a-5<1圯-3<a<2,即a∈(-3,2).
教学的有效性:抽象函数的问题,对新生而言有很多类似的问题,引导学生发现错误产生的原因并利用错误产生的效应进行有效的讲解和举一反三的巩固尝试,能从基础层面理解、接受抽象函数,使其不再成为教学的难点.就本题而言,对函数的单调性的判断是一个关键点.不会运用条件x>0时,(fx)>1.构造不出(fx2)-(fx1)=(fx2-x1)-1的形式,找不到问题的突破口.第二个关键应该是将不等式化为(fM)<(fN)的形式.解决此类问题的易错点:忽视M、N的取值范围,即忽视(fx)所在的单调区间的约束.
2.整合能力错误效应
有别于基本功的错误,教学需要面对的凌驾于基本功之上的数学学习错误.这里笔者要谈的正是整合能力方面的错误.整合能力,是学生学习到一定程度而言,将知识进行系统化后出现的.这方面的错误效应,其错误的体现相对级别更高、难度更大,要求教师精心分析学生错误产生的缘由,并在整合能力上对教学进行下一步的思考,来提高知识衔接处的教学有效性.
案例2(2014年省统测卷压轴文)已知m∈R,设函数f(x)=x3-3(m+1)x2+12mx+1.求:(1)若f(x)在(0,3)上无极值点,求m的值;(2)若存在x0∈(0,3),使得f(x0)是f(x)在[0,3]上的最值,求m的取值范围.
学生错误成因:这是最新的本省2014年统测卷上的导数压轴题.其第(2)问的得分率是均分2分,难度系数0.16,笔者对本题做了一些统计和难点分析,并对部分错误做了归纳:
(1)第(1)问错误典型集中在对函数f(x)在(0,3)上无极值点的含义不理解,部分学生在解三次函数问题时忽视函数无极值的情形,对我们三次函数教学提出了全面性的要求;
(2)第(2)问是难点和易错点.其错误的总体来说,体现在:其一,中低端学生对题意理解不到位,无从下手,很多学生不理解何为存在x0∈(0,3),使得f(x0)是f(x)在[0,3]上的最值?函数在闭区间上存在最值的最基本要求忽视——端点值和极值;其二,中高端学生错误集中在对分类讨论思想的全面性处理上,往往只能分析某一种或两种情形,还未能解决好运算的问题.
善用错误效应:本题是不可多得的一道典型好题,是利用错误效应教学提高有效性的典型问题.教师对问题分析要集中关注下面几点,提高整合问题教学的有效性:
(1)函数闭区间的最值可能出现在哪些点处?
(2)动态函数讨论最值,最需要关注极值点与区间的动态变化,属于典型的动函数定区间问题.
(3)分类讨论思想渗透进教学,对函数问题进行层层剥离式的分析,可以从区间[0,3]上极值点的个数下手进行分类,即两大类四小类.
(4)运算环节是获得高分的基本保障,教师教学要板演进而提高学生解决问题的真实性.
解析:(1)由题意知f′(x)=3x2-6(m+1)x+12m=3(x-2)(x-2m),由于f(x)在[0,3]上无极值点,故2m=2,所以m= 1.
(2)由于f′(x)=3(x-2)(x-2m),故
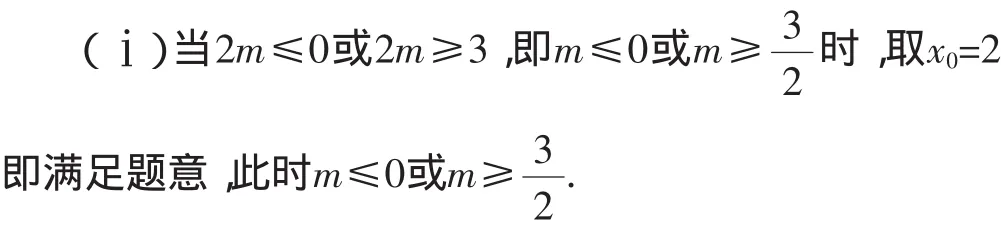
(ⅱ)当0<2m<2,即0<m<1时,列表如下:

x 0(0,2 m) 2 m(2 m,2) 2(2,3) 3 f′(x) + 0 - 0 +f(x) 1 单调递增极大值单调递减极小值单调递增 9 m+1


x 0(0,2) 2 (2,2 m) 2 m(2 m,3) 3 f′(x) + 0 - 0 +f(x) 1 单调递增极大值单调递减极小值单调递增 9 m+1

教学的有效性:整合性问题是错误较多的问题,但又是值得教师挖掘和关注的问题,从整合性问题中得到的典型错误,将这类错误的效应集中体现在教学之中,既丰富了教学的真实性也提高了整合性问题教学的有效性.
总之,本文在数学基本和整合的角度谈了问题的错误效应,以及结合案例,从错误成因出发并做出合适的解析,既水到渠成又自然而然,并利用错误提升教学有效性的两个方面.限于时间和篇幅,着重以“基本功的错误效应、整合性问题的错误效应”视角出发,以错误为载体寻求应对这些典型错误的方法展开叙述,期间还有很多问题没有涉及,还有一些方面笔者未能从自身的教学实践中提炼、总结出来,期待读者补充.以上的笔者管窥之见,希望能够不吝赐教.
1.崔景南.当学生偏离教师航向时[J].数学通报,2008(9).
2.曹军.高中函数教学中避免不了的五个问题[J].中学数学杂志,2013(7).
3.展国培.有效教学,从关注学生开始[J].中小学数学(高中),2013(1).

