螺旋埋弧焊管焊接过程的三维数值模拟

晁利宁 ，毕宗岳 ，鲜林云 ，余 晗 ，张晓峰 ，张国超 ，李鸿斌 ，汪海涛 , 马 璇

（1.国家石油天然气管材工程技术研究中心，陕西 宝鸡721008；2.宝鸡石油钢管有限责任公司 钢管研究院，陕西 宝鸡721008）

螺旋埋弧焊管是以热轧钢板做坯料，经过铣边、成型、内外焊接、机械扩径等工序而制成的钢管，质量好，可靠性高[1]。焊接是螺旋埋弧焊管的核心工序之一，尤其是石油天然气用钢管，对质量要求高，焊接量大，同时还要求在确保焊接质量的前提下，尽可能提高焊接效率[2]。螺旋埋弧焊管焊接过程中熔池的动态行为是通过母材的温度场和焊接电弧的热输入表现的，但焊接过程温度场变化是瞬时的，熔池存在时间也十分短暂，用常规试验手段很难检测焊接温度场的实时变化情况。随着数值模拟技术的发展，利用有限元模拟的方法可以快速、准确地得到焊接温度场的分布，并预测其动态变化过程[3-4]]。因此，利用有限元模拟研究焊接过程中温度场的分布对调整焊接工艺有着重要意义[5-6]。

本研究利用有限元分析软件ABAQUS，通过FORTRAN语言编写子程序DFLUX，建立了双丝埋弧焊有限元计算模型，实现了双椭球热源模型加载处理，进行了瞬态温度场数值模拟研究。

1 焊接物理模型的建立

1.1 温度场控制方程

在区域Ω中的热传导控制方程为[7]

式中：Cp—比热容；

λ—热导率；

Q—内热源强度；

T—温度；

t—时间。

焊接温度场控制方程的热流边界条件如下。

（1）对流换热产生的边界上热流

式中：qc—热流率；

αc—对流换热系数；

T—固体表面温度；

TOC—环境参考温度 。

（2）辐射换热导致的边界对流

式中：qr—热流率；

σ0—黑体辐射常数；

ε0—黑度（发射率）；

T—辐射面温度；

TOR— 环境参考温度 。

1.2 应力场控制方程

在该区域中力平衡方程为

式中：σij,j—应力分量，亦包括热应力项。

热应变可按下式描述

式中：εij

r—热应变张量；

αij—热膨胀系数；

To—参考温度；

δij—δ算子。

1.3 建立热源模型

准确的热源模型能较好地表现焊接过程中的传热行为。热源模型对焊接温度场和应力场的分布，特别是靠近热源的部位有很大影响。

在椭球形热源密度函数计算过程中发现，椭球前半部分温度梯度不像实际中那样陡峭，而椭球的部分温度梯度分布较缓。为了克服这个缺点，Goldak提出的双椭球模型通过对热源前后两部分分别采用不同的函数进行描述，使得热源模型能够很好地反映热源前后两个1/4椭球的热流密度梯度之间的差异，与实际的电弧热源更为接近，因此，被广泛应用于电弧焊的数值模拟中[8]。

以（0，0，0）为中心，平行于坐标轴（x，y，z）半径为a,b,c的双椭球模型[9]前半部分是1/4椭球，后半部分是另一1/4椭球，两部分椭球的能量分配系数分别为f1和f2，且f1+f2=2，其热源分布分别为

根据给定的焊接工艺参数，按照双椭球热源模型函数计算出各节点的热流密度，并将其施加于所选节点上。当电弧中心移动时，重复施加各节点热流密度，从而实现热源的移动。

2 有限元计算模型的建立

本研究模拟的是螺旋埋弧焊管的焊接过程，工程实际中焊管外径为1 219 mm，壁厚为22 mm。

螺旋埋弧焊管一般采用多丝埋弧焊，先焊接内坡口（简称内焊），后焊接外坡口（简称外焊），二者相差一个螺距的焊接时间。因此建立一个螺距的管体长度，为1 693 mm。管体开X形坡口，内焊坡口角度为60°，外焊坡口角度为90°，钝边为10 mm，几何模型如图1所示。

图1 螺旋焊管的几何模型

2.1 焊管焊接热物理性能参数

焊接是一个局部快速加热到高温，并随后快速冷却的过程，随着热源的移动，整个焊接温度随时间和空间急剧变化，材料的热物理性能也随时间和空间急剧变化[10]。

本研究假设焊材和母材的材料相同。材料参数如图2所示，图中CP为比热容（100 J/kg·℃），K为导热系数（10 W/m·K），α 为线膨胀系数（10-5/℃），σs为屈服强度（100 MPa），E 为弹性模量（104MPa），G为切变模量（105MPa），另外在参数中假设不随温度变化[11]的是密度（7800kg/m3）和泊松比（0.3）。

图2 材料性能参数

2.2 边界条件的处理

计算温度场时给焊件表面施加对流和辐射，温度越高，辐射换热的作用越强烈。此处将辐射换热与对流换热通过一个总的换热系数β一起考虑，边界换热损失的热能表示为qs=β(T-Ta)[12]。取对称面为绝热边界条件，初始温度设定为25℃。

2.3 网格划分

为了准确预测焊接温度场的分布，建立与实际结构尺寸完全相同的三维有限元模型。模拟焊管规格为φ1 219 mm×22 mm，取管长1 693 mm。并建立内外焊熔敷金属和焊管母材。采用不均匀网格划分方法，在焊缝及其附近区域采用较细的网格，而在远离焊缝处采用较粗的网格，保证计算速度和精度。有限元模型如图3所示。

图3 有限元模型网格划分

选用热单元DC3D8，8节点六面体线性完全积分单元，共有单元170 943个，节点222096个。

2.4 焊接工艺参数

焊接采用双丝埋弧焊，分为内焊和外焊两部分。焊接顺序为先内焊，再外焊，内外焊之间相差一个螺距的时间。焊接工艺参数见表1。

表1 焊接工艺参数

2.5 热弹塑性有限元计算

在进行有限元分析计算时，假设材料遵循热弹塑性和双线性本构模型以及Von Mises屈服准则[13-14]。同时，分析中只考虑温度场对结构的弱耦合作用，而不计结构对温度场的影响，即所谓“间接耦合”的方法：先计算焊接温度场，保存每一步计算结果，再把温度场计算结果作为体载荷施加到结构计算中。

另一方面，为了描述焊接中焊缝从 “无”到“熔化金属”，以及最终凝固的过程，本研究采用了“生死”单元技术[15-16]，即首先将内外焊缝中所有单元 “杀死”，相当于焊前的装配状态。在计算过程中，按照实际焊接顺序，将被“杀死”的单元“激活”，模拟焊缝金属的填充。

图4 内、外焊的温度场分布云图

在焊接阶段，通过加载DFLUX子程序的方法完成热源中心螺旋曲线移动。先定义三维表格数组参数来储存不同时刻和不同位置的热流密度值。加载求解之前，先将不同时刻和不同位置的热流密度值储存在表格参数中。热源的移动以步进方式处理，在求解计算过程中，当电弧热源从一个时间步移动到下一个时间步时，求解器将自动从表格参数读取下一载荷步各个节点的热流密度值。覆盖上一载荷步的热流密度。在焊接加热阶段，采用较小的时间步长，设定值为0.1 s，进入冷却阶段求解后，首先获取焊件的最高温度，根据最高温度值重新定义下一个步长，进行求解计算。

3 计算结果及分析

3.1 焊接温度场计算结果

内、外焊温度场的分布云图见图4。从图4（a）到图4（d）可以看出，随着焊接的进行，温度场不断向前移动，内焊的最大温度值为2 065℃，在加载热源的过程中存在着传导及对流行为，使得在完成时模型的整体温度较高，最小温度为87℃。

在焊接过程中焊缝附近的温度梯度极大，而且温度很高，可以达到材料的沸点。远离焊缝的区域，温度变化相对平缓很多。不同焊道相邻的节点经历不同的加热和冷却过程，一些节点已处于冷却阶段（收缩），而另一些节点却处于加热阶段（膨胀），从而产生复杂的非弹性变形，导致残余应力的产生。

从图4中可以看出，焊接温度场分布范围不是很广。这是因为相对于整个构件来说，焊缝热源非常小，而且焊接过程是个瞬态的过程，焊接的加热和冷却时间非常短，热量来不及扩散；降到室温的时候，温度场达到一个稳态的过程，因此温度分布范围比较大，较符合实际。

为了能较清楚地观察温度场的分布规律，本研究提取焊缝附近不同位置节点的温度，绘制热循环曲线。内焊时距离焊缝不同距离处各点位置及热循环曲线如图5所示。

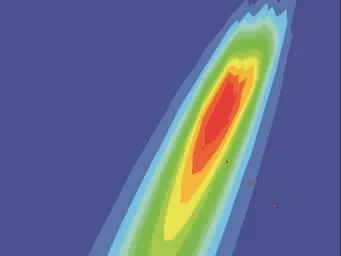
图5 垂直于焊缝方向不同位置的焊接热循环曲线

由图5可以看出，在焊接过程中热源沿焊件的某一个方向移动，焊件上热源能量所及的任一点的温度都要经历由低到高的升温阶段，达到峰值后又经历由高到底的降温阶段，如图5（b）所示。离焊缝中心越近的点，其温度上升的越快，达到的峰值温度越高，温度下降的也快，并且温度上升速度要比温度下降速度大得多，温度梯度较大。热源中心的温度首先达到峰值，并且在热源过后进行冷却；而距离热源5 mm处，由于热源移动到此处的影响，也迅速升温到1100℃左右，随着热源的离开而逐步降温。距离热源中心较远距离的10 mm和15 mm的各点，峰值温度相对较低，分别为600℃和300℃左右。随着焊接热源的远离，温度下降较快，但没有升温时迅速，焊接后随着冷却的进行，温度变化趋于平缓。

沿焊缝方向距离热源不同位置各点温度场分布结果如图6所示。从图6可以看出，随着焊接的进行，热源不断移动，焊缝中心线上各点依次达到焊接的最高温度，同时由于热量的累积效应，使得后面各点的温度较前面各点的温度有所提高。距离热源中心120 mm处，随着焊接时间的延长，热源首先达到这里，并且加热速度非常快，在峰值温度停留时间（保温时间）极短，冷却速度也十分快。随着时间的推移，热源移动到距离热源中心80 mm的地方，其热循环曲线的峰值相对于前一条曲线的峰值要滞后一些，这是因为热源移动到此处的时间较晚的缘故。

图6 平行于焊缝方向不同位置的焊接热循环曲线

4 结论

（1）利用DFLUX程序实现双椭球热源的移动，并结合 “生死”单元技术，使焊接过程的模拟更加接近实际。

（2）焊接过程中，焊缝附近温度梯度很大，在远离焊缝的地方温度梯度渐渐趋于平缓；随着焊接热源的移动，温度中心也随之移动，最高温度可达母材的熔点；在每一道焊接结束后，温度迅速下降，越接近层间温度，降温所用的时间也越来越长。

（3）通过控制焊接速度和焊接电流等不同工艺参数模拟温度场，可以得到不同参数下的熔池尺寸，优化焊接工艺参数，减少试验数量。

[1]潘家华.管道输送钢管的发展趋势[J].焊管,1994,17(02)：1-4.

[1]TUSEK J.Submerged Arc Surfacing with a Multiple-wire electrode[J].Metalurgija，2002，41(04)： 295-300.

[3]刘兴龙，曲仕尧，邹增大.基于ANSYS的焊接过程有限元模拟[J].电焊机，2007，37(07)：41-44.

[4]罗金华，梁晓燕，王春明.中厚板多道焊温度场和应力场三维数值模拟[J].电焊机，2006，36(08)：32-35.

[5]谭险峰，张华.焊接温度场和应力场的热弹塑性有限元分析[J].塑性工程学报,2004,11(06)：71-74.

[6]黄嗣罗，薛勇，张建勋，等.管对接全位置焊应力应变场三维有限元数值分析[J].焊接学报,2006,27(04):73-75.

[7]莫立春，钱百年.焊接热源计算模式的研究进度[J].焊接学报，2011，32(11)：89-95.

[8]陈家权，肖顺湖.焊接过程数值模拟热源模型的研究进展[J].装备制造技术，2005，03(01)：10-14.

[9]GOLDAK J,CHAKRAVARTI A,BIBBY M.A New Finite Model for Welding Heat Source[J].Metallurgual Transactions，1984，15B(02)： 299-305.

[10]ZHU X K， CHAO Y J.Effect of Temperaturedipendent Material Properties on Welding Simulation[J].Computers and Structures，2002，80(11)： 967-976.

[11]TENG T L，LIN C C.Effect of Welding Conditions on Residual Stresses Due to Butt Welds[J].International of Pressure Vessels and Piping，1998，75(12):857-864.

[12]徐琳，严仁军.T形焊接接头残余应力与变形的三维数值模拟[J].江苏船舶，2007，24(01)：5-8.

[13]张玉凤，霍立兴，董俊慧.低碳钢管管道焊接残余应力有限元分析[J].焊接，2000（12）：11-15.

[14]王富耻，张朝晖.ANSYS 10.0有限元分析理论及工程应用[M].北京:电子工业出版社,2006：271-272.

[15]高耀东，何雪.基于ANSYS单元生死技术的焊接模拟[J].热处理技术与装备，2010，31(01)：51-54.

[16]TENG T L，LIN C C.Effect of Welding Conditions on Residual Stresses Due to Butt Welds[J].International of Pressure Vessels and Piping，1998，75(12)： 857-864.