磁滞回线测量方法与Simulink仿真分析研究

曹鸿泰，黄汝霖，姚缨英

(浙江大学电气工程学院，浙江杭州310027)

0 引言

磁滞回线是描绘铁磁性材料磁化性质的重要曲线，也是制造、选择铁磁材料的重要依据，在工程领域有着重要的应用。测量磁滞回线的方法包括霍尔法等直接测量法和RC 积分法等间接测量法。

目前学者对磁滞回线测量已经有一些研究，主要成果有:使用特斯拉计的磁滞回线测量［1-2］，采用反相积分器［3-4］或锁相放大器［5］等运放电路测量磁滞回线，采用电容积分法PSpice 仿真非线性磁芯磁滞回线［6-7］，采用示波器的RC 积分法测量磁滞回线［8-9］，利用Matlab 进行电网合闸磁滞回线仿真［10-11］，也有利用启发式算法测量和辨识磁滞回线［12-13］。从中可以看出，直接测量往往需要昂贵的实验设备，操作较为繁琐;而间接法通过测量电压电流关系来获得磁滞回线，其中积分测量法被广泛采用。积分法虽然具有线性度好、准确度高、测量过程简便等优点，但是至今没有明确的参数计算方法。

实物实验往往需要昂贵的成本和较长的周期，而通过计算机软件仿真测量过程则可大大降低实验成本，提高测量效率。Simulink 是Matlab 中进行动态建模与仿真的集成软件包，其中有针对电力系统的可视化建模与仿真工具库电力系统模块库(power system blocksets，PSB)，是解决电力系统中一些复杂的非线性仿真问题的有效方法。

本研究基于RC 积分法测量磁滞回线，利用Matlab 的Simulink 仿真系统中的电力系统模块库(power system blocksets，PSB)里的饱和变压器模型，并对RC积分测量方法进行深入分析后，通过求解时域微分方程，提出测量电路参数的确定方法。仿真结果的准确性分析以及简易实验结果表明，本研究提出的参数计算方法正确而且有效。

1 测量原理

为了测量饱和变压器铁芯的磁滞回线，本研究设计的RC 积分器测量电路如图1所示。该电路在变压器原边接入一个电阻(R1)，通过电阻上的电压取样u1，反映铁芯中磁场强度H 的变化;在副边接入RC 积分器(R2、C2)，通过RC 参数的适当选取，利用电容C2上的电压取样u2，反映铁芯中磁感应强度B 的变化。最后，利用虚拟示波器观察u1和u2的李萨如图形即得到了变压器铁芯的磁滞回线。由于是间接测量，需要分析u1，u2分别与H，B 呈线性关系的条件。

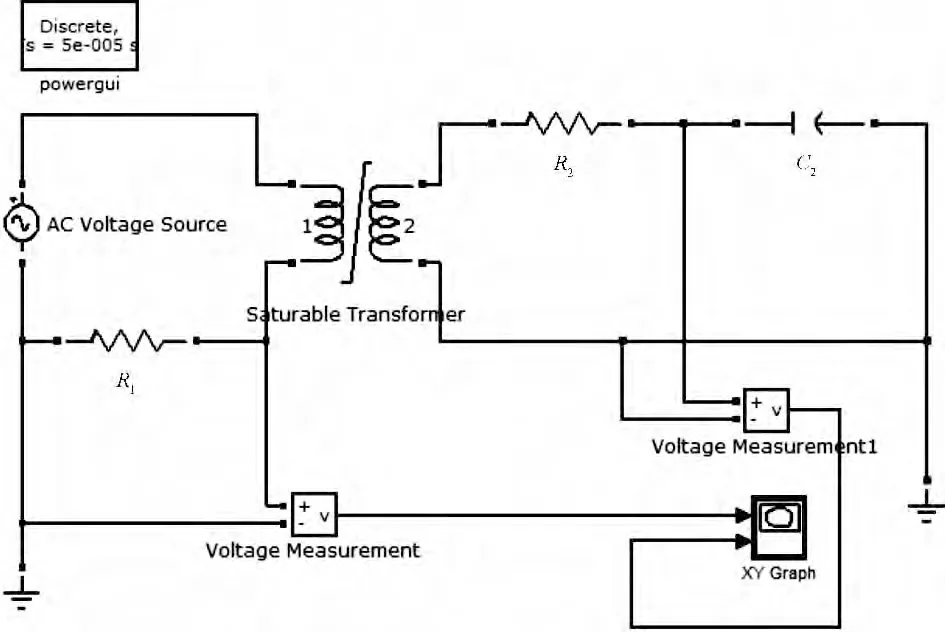
图1 测量饱和变压器磁滞回线电路原理图

记原边线圈N1匝，变压器截面周长为l，记副边线圈N2匝，内阻为r2，变压器截面积为S。

对原边由安培环路定律得:

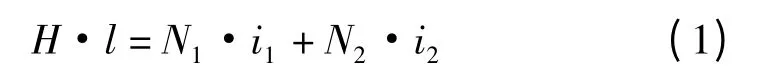
若变压器负载很小，即:

根据欧姆定律可得R1两端电压为:

上式表明:满足条件式(2)时，u1与磁场强度H 为线性关系。

对副边由法拉第电磁感应定律，感应电势为:

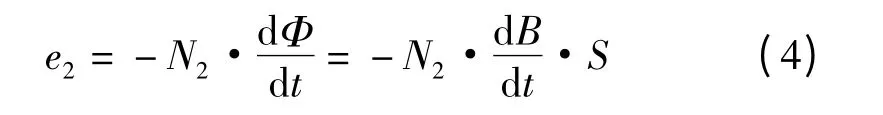
若取原边电流流进同名端，副边电流流出同名端为参考方向，根据KVL，副边回路满足:

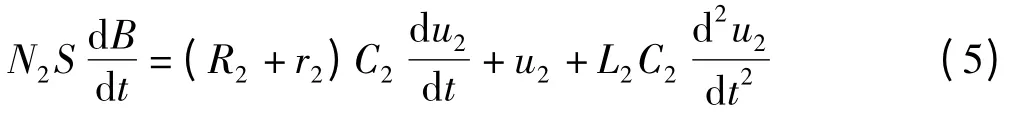
当且仅当以下不等式:

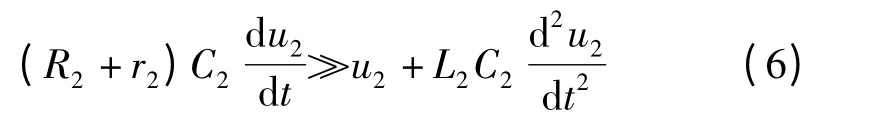
成立时:

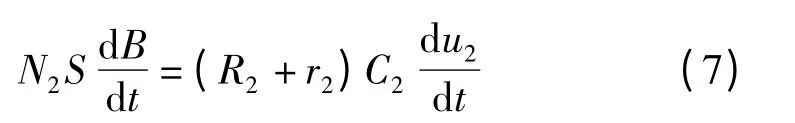
解常微分方程，得:

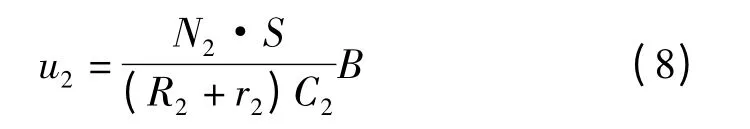
上式表明:满足条件(7)时u2与B 是线性关系。

在同时满足条件式(2，7)时，以u1和u2分别为X轴与Y 轴作李萨如图形，由于它们分别与H 和B 呈线性关系，则李萨如图形就表示出饱和变压器的磁滞回线。

2 基于Simulink 的仿真测试

本研究利用Matlab(R2010b 版本)中的Simulink进行建模，建模步骤如下:

(1)建立一个新的模型窗口，同时打开Simulink的电力电子(SimPowerSystems)模块工具箱，进行仿真测量模型的搭建。

(2)打开元件(Elements)模块组，复制一个饱和变压器模型Saturable Transformer 到建模窗口中，模型参数不变。

2.1 饱和变压器模型说明

打开Parameter 选项卡，调节参数显示方式为SI(即国际单位制)，以下对饱和变压器的参数作出说明。饱和变压器模型参数如图2所示。

第1 行数据表示饱和变压器的设备容量和工作频率，图中参数表示变压器的设备容量是250e6 VA，工作频率是50 Hz。

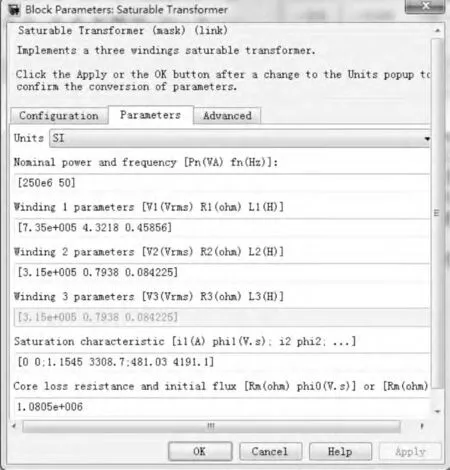
图2 饱和变压器模型参数

第2 行数据表示饱和变压器的原边线圈的饱和电压、电阻和电感，图中参数表示变压器原边线圈的饱和电压是7.35e5 V，电阻是4.321 8 Ω，电感是0.458 56 H。

第3 行数据表示饱和变压器的副边线圈的饱和电压、电阻和电感，图中参数表示变压器副边线圈的饱和电压是3.15e5 V，电阻是0.793 8 Ω，电感是0.084 425 H。

第5 行数据表示饱和变压器的模型参数，保持不变即可;第6 行数据表示铁芯损耗电阻Rm，保持不变即可。

2.2 电路模块搭建与参数设定

打开电源(Electrical Sources)模块组，复制交流电压源模块AC Voltage Source 到建模窗口中。仿真磁滞回线，AC 参数应当满足超过变压器的原边额定电压，才能使变压器磁路饱和。AC 交流电源参数可以分别设定为10e5* sqrt(2)(单位:V)，90(单位:deg)，50(单位:Hz)，Sample time 为0(单位:s)。

打开元件(Elements)模块组，复制3 个串联RLC支路模块到建模窗口中，下面对器件参数选择进行说明。R1为原边取样电阻，不应很大，可取1e3(单位:Ω)，L 为0(单位:H)、C 为inf(单位:F)，作为原边取样电阻R1。其余两个串联RLC 支路模块参数可以先设置R2参数为R 为400e3(单位:Ω)、L 为0(单位:H)、C 为inf(单位:F)，设置C2参数R 为0(单位:Ω)、L 为0(单位:H)、C 为10e-6(单位:F)，作为副边的RC积分器的电阻R2和电容C2。

打开测量(Measurements)模块组，复制两个电压测量模块Voltage Measurement 到建模窗口中，分别用于测量原边取样电阻R1和副边RC 积分器的电容C2上的电压。

打开基本仿真(Simulink)模块工具箱，从输出(Sinks)模块组，复制一个XY 型通道示波器XY Graph，设置X 轴为±6e4，Y 轴为±6e2，用于观察原边取样电阻R1和副边RC 积分器的电容C 上的电压所形成的李萨如图形，即B-H 曲线。

打开电源系统(SimPowerSystems)工具箱，复制一个powergui 模块，双击打开，设置Configure parameters中的Simulation type 为Discrete，Sample time 设置为50e-6(单位:s)。这是因为仿真类型选择离散型，可以得到更加平滑的磁滞回线，仿真速度也更快。

在菜单栏Simulation 中，设置Configuration Parameters 中的Stop time 至少大于0.04(单位:s)。设置Solver 为ode23tb 算法。

进行适当连接后，即得到利用RC 积分器观测磁滞回线电路的模型。

3 RC 积分器的参数设置

积分器测量方法需要满足式(3)和式(8)两个线性关系，则必须有式(2)和式(6)成立。当实验参数不满足线性关系时，虚拟示波器中不能得到正确的磁滞回线。下面具体分析测量电路的参数选取。

饱和变压器模型铁芯电路模型中的有功损耗电阻，即为涡流损耗，由式(2)成立，则有i2≈0 A，这表明应使变压器工作在接近空载状态，此时满足u1与H 为线性关系。

在时域上求解微分方程，可找出不等式(6)成立的条件。电源电压可用uS=Amsin(ωt+90)表示，则电容电压可表示为u2=Kmsin(ωt +φ)，则不等式(6)可化简为:

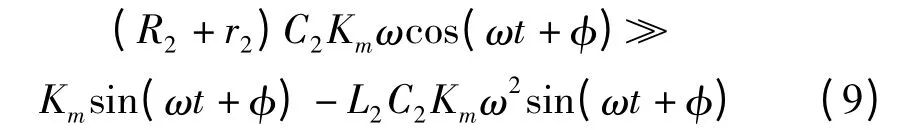
则应使后两项与第一项的比值尽可能小，如下式所示:

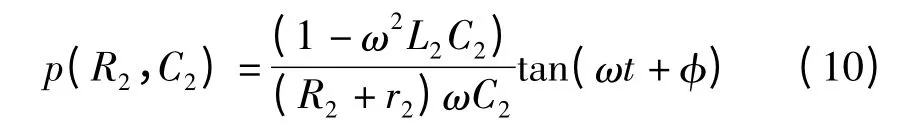
由于式(10)右边三角函数tan(ωt +φ)在一个周期内是发散的，为使比值尽可能小，只能令其系数趋近于0，才能满足式(8)，从而电容电压u2与磁感应强度B 为线性关系。

通过Simulink 进行饱和变压器磁滞回线的仿真采用离散仿真模式，因此只需满足正切函数p(R2，C2)在一个周期里有足够长的时间近似为零，就可以得到饱和变压器铁芯的磁滞回线。为了保证仿真准确性，可取上述条件的一个近似等价条件为|p| ＜0.1 在99%的周期内成立，即:

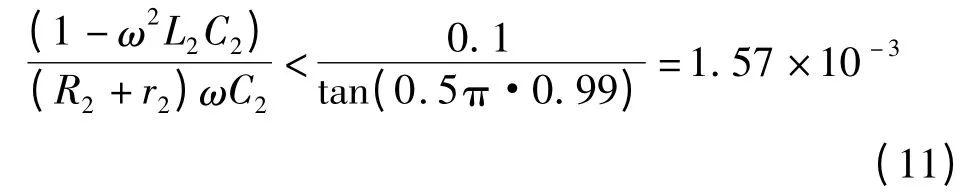
通常r2≪R2可忽略，且在该测量中，L2≈0.08 H，ω=314 rad/s，考虑变压器接近似空载运行，可设定R2为1 000 倍饱和变压器满容量负载电阻，即:

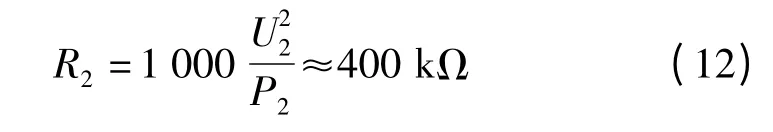
作为积分器电阻值，则解得C2＞4.9 μF。因此，可用C2=10 μF，R2=400 kΩ 作为积分器参数。

上述参数仿真结果如图3所示。

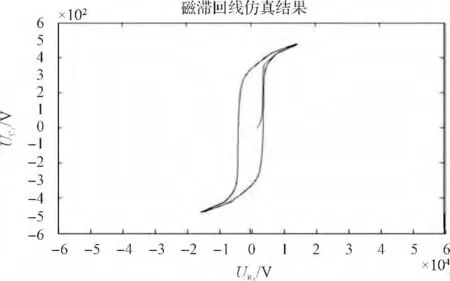
图3 积分器R2=400 kΩ，C2=10 μF 时测得磁滞回线

4 仿真结果与分析

为了考察RC 积分器测量磁滞饱和变压器磁滞回线的准确性，可以用多组磁滞回线绘出饱和变压器的基本磁化曲线，并与Simulink 中的磁滞回线的原始数据对比，以说明本研究所提出的实验模型的正确性和仿真结果的准确度。

笔者分别调整AC 电压源电压(单位:V)为9e5*sqrt(2)，9.5e5* sqrt(2)，10e5* sqrt(2)，10.5e5* sqrt(2)，11e5* sqrt(2)和11.5e5* sqrt(2)进行仿真，可以得到一组磁滞回线。将这些磁滞回线绘在一张图中，并将磁滞回线的拐点标出，用折线段拟合，再经过放大得到的磁滞回线图如图4所示，图4 中包围面积即为铁芯损耗。由于变压器工作在轻负载状态，包围面积变化很小。

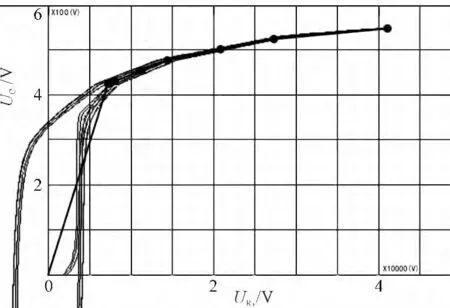
图4 饱和变压器磁滞回线仿真结果(局部)

Simulink 中饱和变压器的磁化曲线数据在hysteresis.mat 文件中，可以绘出模型的基本磁化曲线。根据仿真结果得到的拐点可以绘出测量结果的基本磁化曲线。由于存在线性关系，可将两幅图的坐标轴比例变换，合并为一张图，测量结果与模型值吻合，基本磁化曲线测量误差对比如图5所示。

图5 基本磁化曲线测量误差对比

利用折线插值方法可以得到对应拐点处的相对误差值，其相对误差表明本研究提出的方法的测量结果与饱和变压器模型值非常接近。根据本研究提出的计算RC 积分器参数方法得到的测量误差小于1.6%，而且这个误差由式(15)控制。

因此，只有当R2、C2满足式(11，12)时，才满足测量要求中的线性关系，才能满足适用RC 积分法的前提条件。

5 实验验证

为了进一步验证仿真方法的可操作性与正确性，根据本研究提出的参数确定方法，笔者设计了RC 积分法测量电路，通过实验室测量得到了工频变压器的磁滞回线。

实验所用变压器为上海祥华电器厂生产的BK -50 控制变压器，高压侧选择额定电压220 V 线圈，低压侧选择额定电压36 V 线圈。高压侧经单相调压器接入市电，串联电阻R1=240 Ω。低压侧串联RC 积分法测量电路，其中R2=200 kΩ，C2=4.7 μF。本研究利用Tektronix TDS 3054C 示波器测量磁滞回线，其中CH1 测量R1两端电压，CH2 测量C2两端电压。观测李萨如图形，BK -50 变压器磁滞回线如图6所示。

实验中测得磁滞回线与仿真结果相一致，从而验证了仿真方法的可操作性与RC 积分器参数确定方法的正确性。

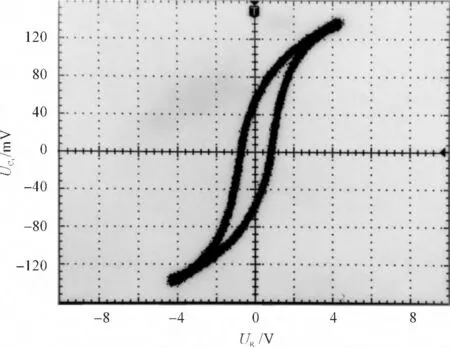
图6 BK-50 变压器磁滞回线

6 结束语

在工程实践过程中，为了得到电力变压器的磁滞回线，需要经过复杂繁琐的操作过程，且往往受到试验条件、测量手段等方面的限制。电力变压器由于额定电压在千伏以上，难以直接实验测量，而通常采用仿真方法得到其磁滞回线。本研究基于Matlab 的Simulink 仿真系统，利用电力系统模块库PSB，采用RC 积分法实现磁滞回线测量。本研究提出的确定参数方法使得最终测量相对误差在1%左右，具有很高的实用价值。

由于Simulink 中饱和变压器模型给出的参数是基本磁化曲线，原边电压存在较小的取值范围。如何解决因原边电压取值问题引起的仿真错误还有待进一步的研究。

在有关交流电量电路分析中，常常需要结合时域分析与频域分析。本研究借鉴频域分析的思想，并就求解时域微分方程和Simulink 仿真方法提出了确定参数的方法，为电路设计提供了参考依据。

［1］孟祥鹏，张建强，徐 静，等.静态法磁滞回线测量实验分析及微观机理解释［J］.实验室研究与探索，2012，31(9):40-44.

［2］王蕴杰.铁磁材料磁滞回线的Matlab 分析方法设计［J］.电脑开发与应用，2012，25(7):51-53.

［3］刘正平，程 蔚.软磁材料磁滞回线在线检测系统［J］.电测与仪表，2010，47(8):16-19.

［4］吕 晔，周洪强.磁滞回线测试系统的硬件电路研究［J］.电测与仪表，2009，46(7):77-80.

［5］SHIRANE T，ITO M.Measurement of hysteresis loop on soft magnetic materials using lock-in amplifier［J］.IEEE Transactions on Magnetics，2012，48(4):1437-1440.

［6］黄子平，王文斗.非线性含磁芯线圈的PSpice 模拟［J］.强激光与粒子束，2004，16(8):1063-1066.

［7］PEDRA J，SAINZ L，CÓRCOLES F，et al.PSPICE computer model of a nonlinear three-phase three-legged transformer［J］.IEEE Transactions on Power Delivery，2004，19(1):200-207.

［8］汪源浚.用示波器和信号发生器检测磁环B-H 磁滞回线的方法［J］.教学与科技，2009(3):7-12.

［9］李都红，张小青，李敬怡，等.一种测量铁磁材料磁滞回线的方法及仿真［J］.变压器，2008，45(4):38-39.

［10］袁兆强，凌 燕.基于Matlab 的变压器仿真建模及特性分析［J］.电力学报，2007，22(2):175-179.

［11］肖伟平，黄绍平.考虑磁滞现象的变压器饱和特性仿真分析［J］.高压电器，2005，41(4):254-256.

［12］何汉林，孟爱华，祝甲明，等.基于优化的GRNN 和BP神经网络的磁滞曲线拟合对比分析［J］.机电工程，2013，30(1):116-120.

［13］MINCHEV S V.Neural networks for modeling of dynamic systems with hysteresis［C］//First Inter- national IEEE Symposium "Intelligent Systems".Varna:［s.n.］，2002:42-47.