扁钢精轧过程的数值模拟与分析研究

赵章风，姚世泽，张 宪，钟 江，沈 斌

(浙江工业大学机械制造及自动化教育部重点实验室，浙江杭州310014)

0 引言

板材轧件是一个复杂的塑性变形过程，既有材料非线性、几何非线性，又有边界条件的非线性，变形机理非常复杂，难以用准确的数学模型来描述。影响其形成的因素主要有轧辊形状、轧件尺寸、材料特性、轧制温度和工艺参数等［1-3］。随着计算机和数值模拟技术的快速发展，计算机数值模拟技术得到了广泛应用［4］。近几年来，有关带钢冷轧有限元数值模拟的报道很多，如徐树成［5］介绍了板带钢轧制常用的有限元模拟方法类型;李传瑞等［6］借助Marc 软件对薄板CSP轧制的第一道次进行了模拟，研究结果表明在轧件变形区内，等效应力沿着轧制方向逐渐变大，中性面最大，后又变小;喻海亮等［7］应用ANSYS/LS-DYNA 软件对带钢精轧过程进行了有限元模拟，对板带精轧过程中不同温度、厚度、压下量的轧制力进行了有限元模拟，并进行模拟计算值和理论计算值进行比较，二者相对误差在11%以内;徐新平［8］主要介绍了针对硅钢片轧制变形的进行了有限元数值模拟，结果表明模拟结果与传统理论所述结果一致;杜凤山［9］分析了宽厚比约为10 的薄板轧制过程;刘立文［10］分析了轧件厚度、压下率及摩擦系数对冷轧板带变形的影响。多道次轧制过程的数值模拟分析，对轧钢机结构优化、制定合理工艺参数、提高轧制效率、确保产品质量具有重要意义。

本研究基于DEFORM 软件［11］建立扁钢轧制仿真模型［12］，对1 个周期动态轧制过程进行数值模拟分析。

1 轧制理论

1.1 咬入条件

轧辊对轧件的作用力和摩擦力如图1所示。轧件与轧辊刚接触时，轧辊给轧件的作用力N 的水平力Nsinα 与轧件进入轧辊的方向相反，轧件被该力力图推出辊缝，而轧辊给轧件的摩擦力T 的水平力，则力图把轧件拖入辊缝。在没有外力强行推入时，轧件被咬入称为自然咬入，其咬入条件是:

在接触面上某点的摩擦力T 和轧辊在该点上的法向压力之比称为摩擦系数f。其值等于摩擦角β 的正切，即:

因此，在下列条件时轧件可以自然咬入，即咬入条件:

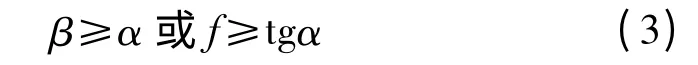
式中:α—咬入角，β—摩擦角，f—轧件与轧辊间的摩擦系数。

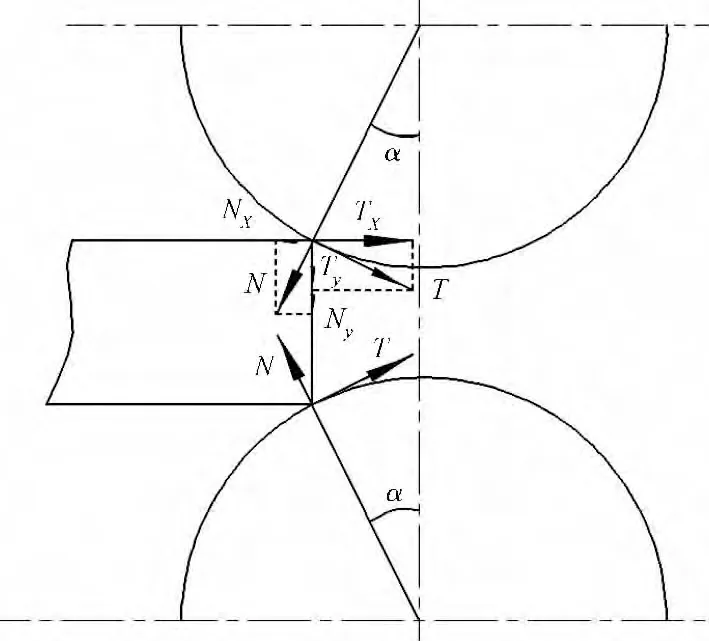
图1 轧辊对轧件的作用力和摩擦力

由以上分析可知，临界条件下咬入角和摩擦角的关系为α=β，水平方向的分力为Tcosα=Nsinα，此时的咬入角α 称为最大咬入角。同理可得:

α ＞β，Tcosα ＜Nsinα，为不能咬入条件;不能自然咬入;

α ＜β，Tcosα ＞Nsinα，为能够咬入条件，可自然咬入。

1.2 稳定轧制的条件

轧件被轧辊咬入后，金属与轧辊的接触表面，一直是连续地增加。假设轧辊对轧件的单位压力沿咬入弧是均匀分布的，则径向力的合力作用点在该段接触弧的中央，轧件进入变形区的受力图如图2(a)所示。

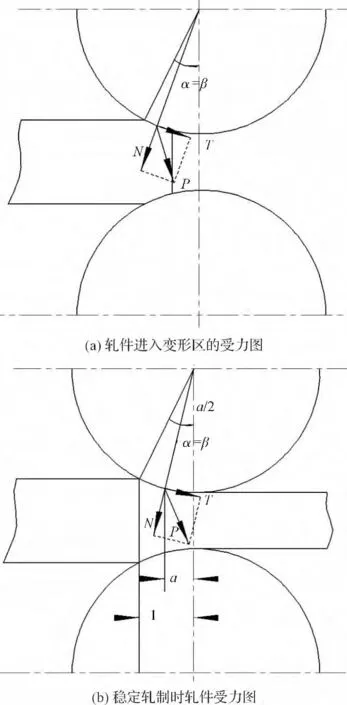
图2 轧件受力图

在轧件充满变形区后，稳定轧制时，轧机受力情况如图2(b)所示。此时剩余摩擦力达到最大值。假设合力作用点在接触弧中部，保持轧件顺利轧制的条件为:

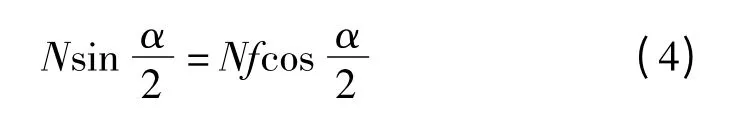
故有:

1.3 轧辊直径的确定

根据轧辊强度及允许的咬入角α(或压下量与工作辊直径之比Δb/D)来确定。即在保证轧辊强度的前提下，同时满足下列咬入条件:

式中:D—轧辊的工作直径，Δb—轧制前、后轧件宽度差，α—咬入角。

1.4 轧制力的确定

轧制压力:

式中:H—轧件与立辊的宽度(即轧件厚度)，l—轧件与轧辊接触弧的水平投影(简称接触弧长)，pm—平均单位压力。

其中:

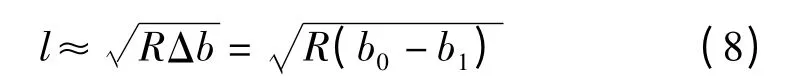
式中:R—轧辊的工作直径;b0，b1—轧制前后轧件宽度。

轧制平均单位压力的基本计算公式采用奥罗万(E.Orowan)-帕斯科(K.J.Pascoe)公式为:

式中:K—平均变形抗力，K=1.15δs。

查《机械设计手册》可知，取屈服极限δs≈235 MPa。

1.5 轧制功率的确定

作用在两个轧辊上的轧制力矩为:

式中:α—咬入角，φ—力臂系数。

其中，φ=β/α≈a/l，l、a 根据图4 可以得知。

不过一般来说，力臂系数也可以近似按以下数据选取:冷轧时φ≈0.35～0.45。

轧制功率:

式中:n—每分钟的转速。

2 有限元模型建立

建立三位实体模型是DEFORM-3D 进行模拟分析的前提，为了有效地比较单、双道次轧制效果，模型参数如表1所示。模型建立如图3所示，其中，扁钢的规格为:宽12 mm～100 mm，厚4 mm～8 mm，材料为:Q235 钢，轧件毛坯为退火状态，所以对应deform 材料库选择AISI-1 015［70-2 000F(20-1 100C)］。为了实现扁钢的顺利咬入，模型中设计了一个推板，以一定的速度作用于扁钢的尾部，当扁钢顺利达到咬入后，推板速度为0，从而使扁钢在摩檫力的作用下进入轧制过程中，轧辊和推板为刚性体，轧辊直径为Φ180 mm。根据生产经验，整个生产过程温度变化不明显，忽略温度对轧件泊松比和弹性模量等的影响。

表1 模型参数(单位:mm)

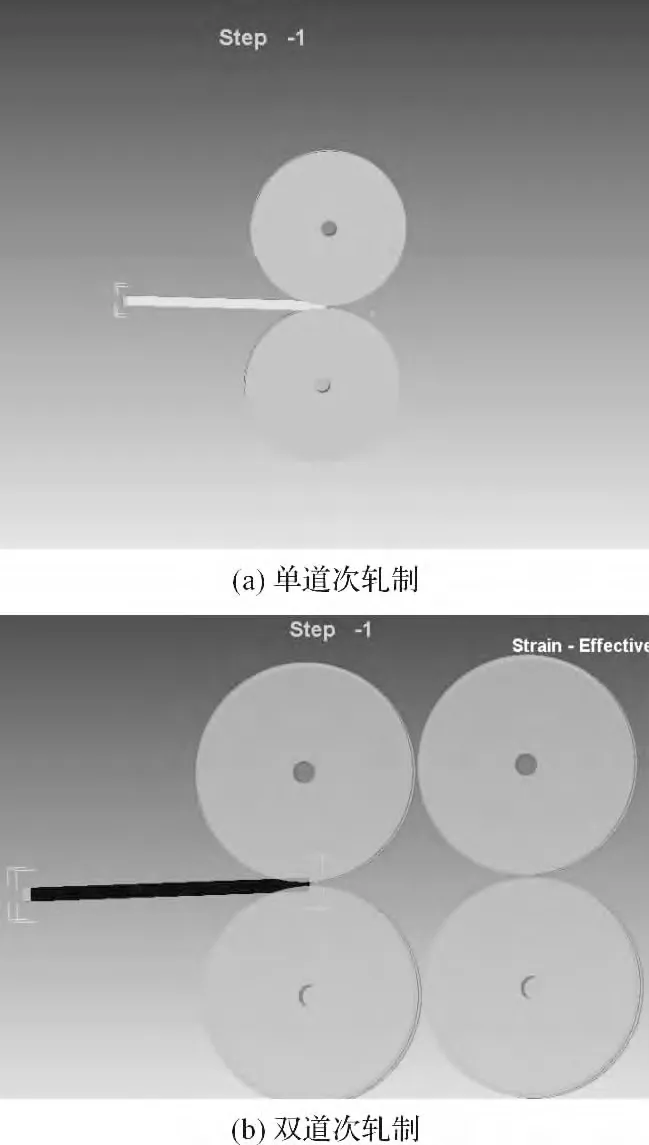
图3 有限元模型

根据轧制过程中体积不变原则，由于轧件厚度变小，在长度方向被拉长，宽度方向发生凸起，中间最大，两边逐渐减小，在这个变形过程中，会产生形体滑移，所以为了定位，轧辊的设计采用的主视图和侧视图如图4所示。

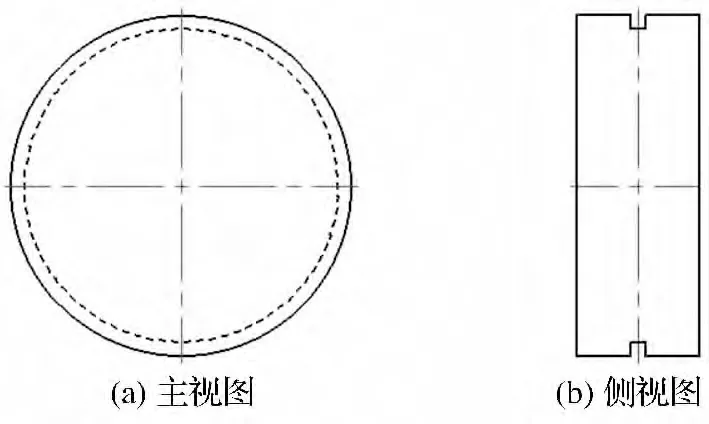
图4 轧辊主视图和侧视图

凹槽不能太深，也不能太浅，如果太深，根据轧制咬入条件，轧辊内半径一定的情况下，轧辊外圆半径就越大，如果太浅，轧件就会在轧制过程中发生跳槽现象，不能进行正常轧制。

3 影响因素分析

扁钢轧制中最重要的目的是提高轧件精度，降低功率。

3.1 轧辊转速的影响

扁钢轧制过程中，轧制速度会直接影响轧制时间，轧制速度越大，轧制时间就越短，同样长度的轧件，轧制精度就会受到影响，同样轧制力也会增加，轧制功率也会变大。轧辊转速对精度、功率的影响如表2、表3所示，随着轧制速度的增加，轧制功率越来越大，同等条件下单道次轧制比多道次轧制功率要小，但是轧制精度却是恰好相反。

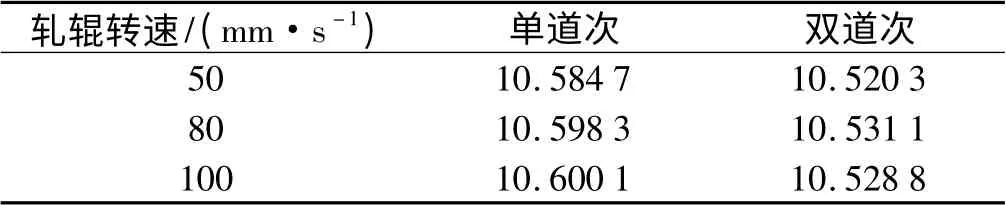
表2 轧辊转速对精度的影响(单位:mm)

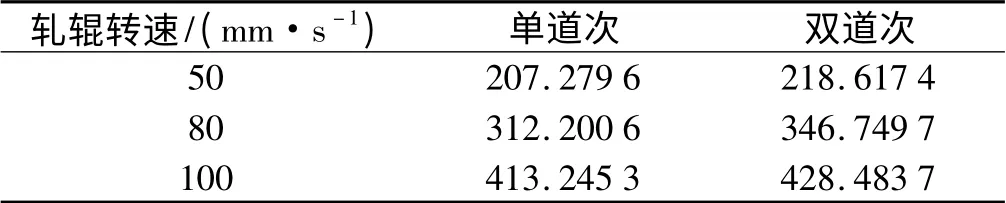
表3 轧辊转速对功率的影响(单位:kW)

3.2 轧件厚度的影响

在其他参数不变的条件下，宽度为12 mm，轧制厚度分别为4 mm，5 mm，7 mm 时，双辊轧制精度比单棍要高，轧制功率随着轧制厚度增加而增加，但是双道次轧制功率要比单道次轧制要高，轧件厚度对精度、功率的影响如表4、表5所示。

表4 轧件厚度对精度的影响(单位:mm)

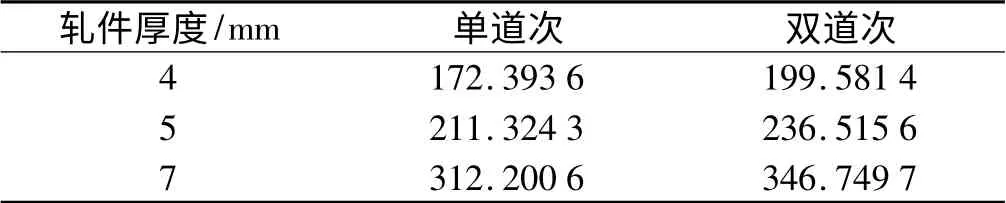
表5 轧件厚度对功率的影响(单位:kW)

3.3 轧件宽度的影响

轧件厚度为7 mm，在相同参数的条件下，当轧件宽度为12 mm、50 mm、80 mm 时，轧件宽度对精度、功率的影响如表6、表7所示，随着轧件宽度变大，单、双道次轧制的精度越来越高，并且双道次轧制的精度比单道次轧制的精度都高，但是功率却比单道次轧制高，不过两者相差的数值随着宽度增加而减小，不过达到80 mm 时，双辊的功率反而比单辊的小。

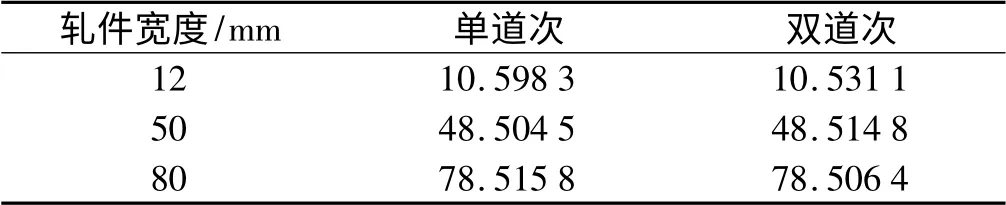
表6 轧件宽度对精度的影响(单位:mm)

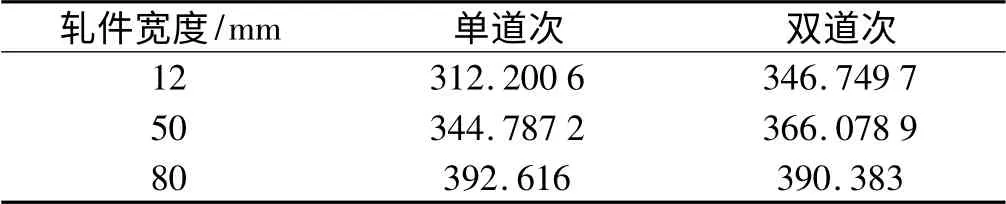
表7 轧件宽度对功率的影响(单位:kW)

3.4 辊径的影响

轧件尺寸厚为7 mm，宽为12 mm，在辊径为90 mm、100 mm、110 mm 而其他参数都相同的条件下，辊径越大，接触弧越大，越易咬入，轧制压力越大，轧制功率也越大，辊径对精度、功率的影响如表8、表9所示。

表8 辊径对精度的影响(单位:mm)

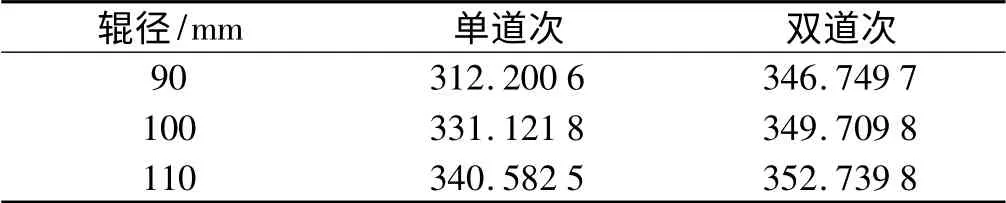
表9 辊径对功率的影响(单位:kW)

3.5 温度的影响

材料在单向拉伸(或压缩)过程中，由于加工硬化，塑性流动所需的应力值随变形量增大而增大。对应于变形过程某一瞬时进行塑性流动所需的真实应力叫做该瞬时的屈服应力，亦称流动应力。如果忽略材料的加工硬化，可以认为屈服应力为一常数，并近似等于屈服极限。实际上，屈服应力是一个由形变速度、形变温度、形变程度决定的函数，且这些参数彼此相互影响，并通常与材料特性相关。材料在不同温度下的流动应力变化曲线如图5所示，由图5 可知，随着温度的增加，应力速率为40 000、8 000 和1 600 之间的差距越来越大，其中曲线从上至下依次为应变速率为40 000、应变速率为8 000 和应变速率为1 600。

在压下量、辊径、轧制速度等条件不变的情况下，轧件的泊松比和弹性模量随着温度的增加而减小。在其他条件不变的情况下，轧件厚7 mm，宽12 mm，在温度分别为20 ℃、400 ℃、600 ℃时，轧制精度随着温度的提高越来越精确，轧制功率也有变小的趋势，随着温度的升高之间的差距逐渐减小，温度对精度、功率的影响如表10、表11所示。

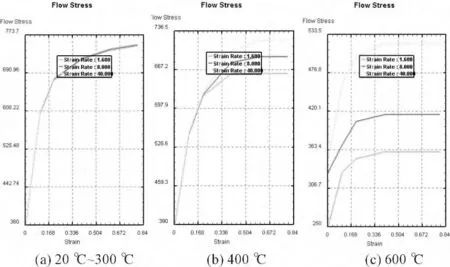
图5 材料流动应力变化曲线

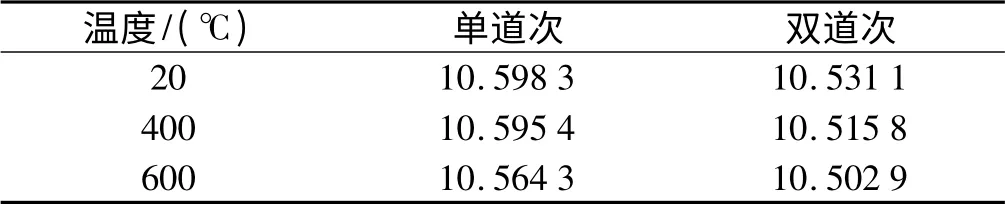
表10 温度对精度的影响(单位:mm)

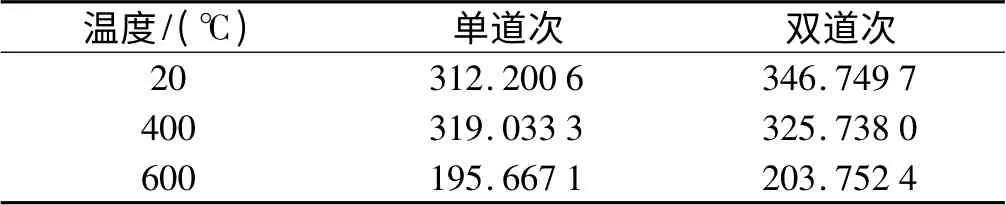
表11 温度对功率的影响(单位:kW)

由表10 和表11 可以看出，双道次轧制比单道次轧制轧制出来的轧件尺寸精度要高。

3.6 压下量的影响

轧件厚度为7 mm，宽度为12 mm，在其他参数都相同的条件下，压下量精度及功率的影响如表12、表13所示。由表12、表13 可知，单道次轧制比双道次轧制的精度低，但是在压下量为0.8 mm、1.5 mm 时，双道次轧制消耗的功率要比单道次轧制大，而在压下量为1.5 mm 时，双道次轧制所用的功率要比单道次轧制小。其中，在压下量为0.8 mm 时，双辊轧制的第一道次压下量为0.5 mm，第二道次为0.3 mm;在压下量为1 mm 时，双辊轧制的第一道次压下量为0.6 mm，第二道次为0.4 mm;在压下量为1.5 mm 时，第一道次压下量为1 mm，第二道次为0.5 mm。

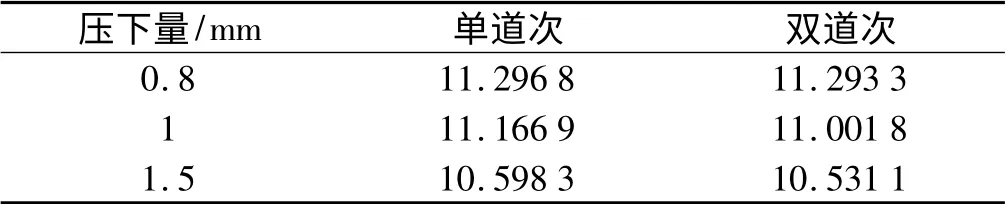
表12 压下量对精度的影响(单位:mm)

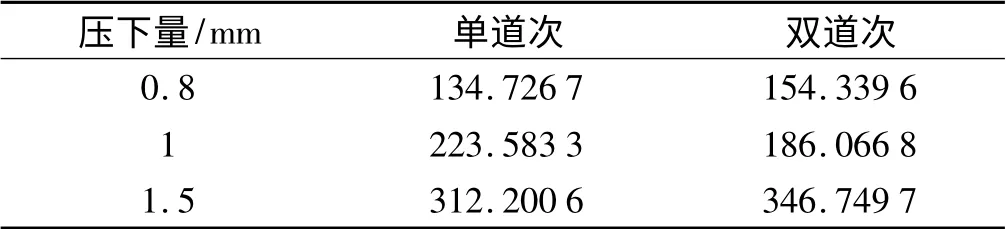
表13 压下量对功率的影响(单位:kW)

表14 压下量对残余变形量的影响(单位:mm)

压下量对残余变形量的影响如表14所示。由表14 可知，相同压下量的条件下，双道次轧制的最大、最小残余变形量比单道次轧制大，这是由于多次分批轧制可以使精度更高。

4 有限元模拟分析

本研究利用DEFORM 软件，采用单、双道次轧制对轧件尺寸为厚7 mm，宽12 mm 的扁钢进行模拟。

4.1 等效应变场分析

两组等效应力图最大、最小等效应变量如图6所示。

图6 等效应变场

表15 单、双道次轧制等效应变场(单位:mm)

单、双道次轧制等效应变场如表15所示。由表15、图6 可知，在相对应的最大、最小等效应变量中，双道次轧制最大等效应变量、最小应变量比单道次轧制的数值大，主要分布在轧件两侧面，特别是扁钢的边缘，中间面变形量较小，轧制接触面变形量比其他面较严重。

4.2 等效应变云图分析

等效应力适合描述应力比较集中的现象，在实际中很难找到真正的单轴拉压的情况，一般结构受力没这么简单，所以在分析的时候需要用等效应力将各主应力进行转换。因此等效应变云图也可以更好地反映轧件变形情况，如图7所示。

图7 等效应力变化云图

表16 单、双道次轧制等效应力(单位:MPa)

由等效应变云图可以看到，在轧制过程中，轧件的受力是不均匀的，如图7(a)、7(b)所示，轧件与轧辊接中间触部位受力较大，边缘变形较大，且单、双道轧制等效应力如表16所示。由表16 可知，双辊轧制明显比单辊轧制等效应力大。

4.3 仿真结果分析

通过对轧件的仿真模拟可以看出，双道次轧制比单道次轧制要复杂，特别是轧件足够长时，轧件既受第1 道次轧制力，同时又要受第2 道次轧制力，由于摩擦力的影响，第1 道次轧制的速度必须与第2 道次的速度同步。

5 结束语

本研究基于DEFORM 软件建立扁钢轧制仿真模型，通过对单道次轧制和双道次轧制的有限元模拟可知，双道次轧制轧件精度要比单道次轧件精度高，但是轧件功率消耗较大，所以对于精度要求高的轧件可以采用多道次轧制工序，以提高轧制精度。因此，在实际生产过程中，还需根据轧件尺寸以及对轧件精度和消耗的功率来合理选定轧制道次。

［1］［苏联］莫施宁.弯卷机和矫正机［M］.北京:机械工业出版社，1958.

［2］施东成.轧钢机械设计方法［M］.北京:冶金工业出版社，1990.

［3］王立萍，李 鸿，李鹏来，等.宽厚板轧制过程有限元模拟分析［J］:机械设计与制造，2011(8):213-215.

［4］钟 江，赵章风，张 宪，等.精密扁钢精整装备的创新设计［J］.机床与液压，2007，35(2):83-85.

［5］徐树成，张金玲，李秀敏.板带钢轧制的有限元模拟分析［J］.湖南冶金，2005，33(5):6-9.

［6］李传瑞，王宝峰，麻永林.CSP 连轧过程金属变形的热力耦合模拟分析［J］.特殊钢，2005，26(6):29-31.

［7］喻海良，赵宪明，刘相华.板带精轧过程轧制力的三维弹塑性有限元分析［J］.钢铁研究，2005(1):14-16

［8］徐新平，王均安.硅钢片轧制过程的有限元数值模拟［J］.上海金属，2005，27(4):30-33.

［9］杜凤山，刘 才，连家创.轧制过程中板形控制的计算机模拟［J］.机械工程学报，1992，28(6):9-13.

［10］刘立文.冷轧板带变形的三维分析［J］.轧钢，1999(3):24-26.

［11］王 涛，倪春华，黄传清.精轧阶梯垫板的厚度与轧辊辊径的联系［J］.机电技术，2012(4):102-103.

［12］杨文兵，姜海峰.基于DEFORM 环件轧制塑性成形过程数值仿真［J］.华中科技大学学报:自然科学版，2006，23(2):56-58.