一类高阶线性微分方程解在角域上的增长性
杨碧珑,易才凤
(江西师范大学数学与信息科学学院,江西南昌330022)
0 引言与结果
本文使用Nevanlinna值分布理论的标准记号[1-2],以 T(r,f)记亚纯函数f(z)的特征函数,N(r,f=a)表示函数f(z)的a值点的密值量,ρ(f)和μ(f)分别表示f(z)的级与下级,用δ(a,f)表示函数f(z)在点a的亏量等.
关于亚纯系数高阶线性微分方程
非零解在全平面上的增长性已有很多研究,本文主要讨论此类方程的解在某些角域上的增长性.
论文的证明需要用到角域上特征函数的相关性质[3-4].
假设f(z)是角域Ω(α,β)上的亚纯函数,其中
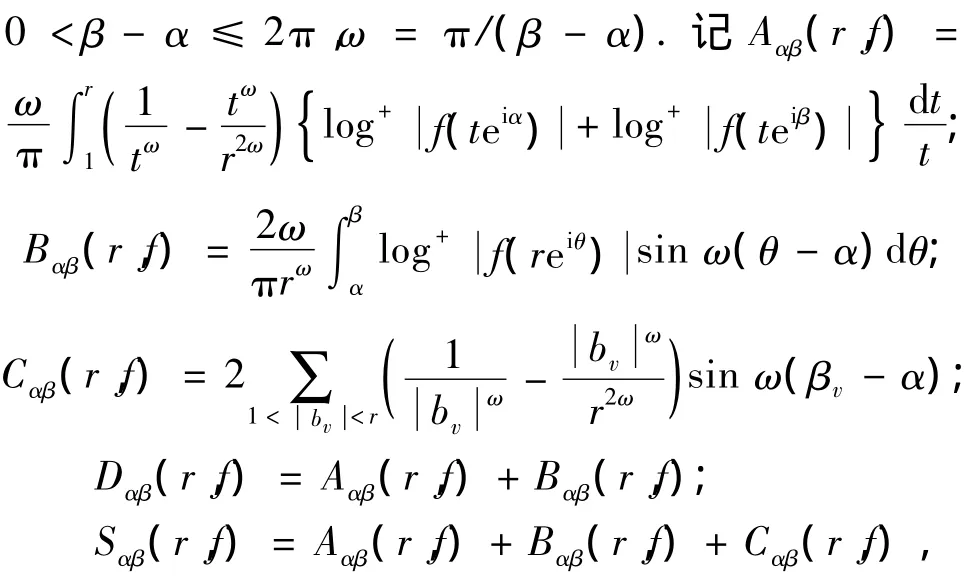
亚纯函数f(z)在角域Ω(α,β)上的增长级和下级依次定义为
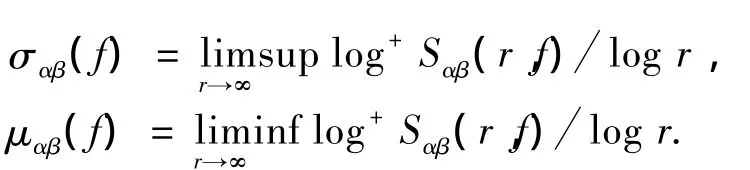
下面定义角域上的Ahlfors-Shimizu特征函数[5],令

定义
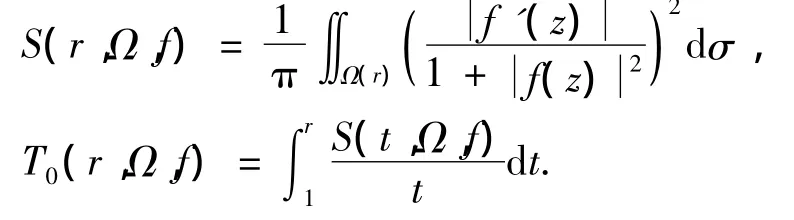
并运用Ahlfors-Shimizu特征函数定义了f(z)在角域Ω(α,β)上的级和下级:

然而这2种不同定义的增长级存在一定的联系,根据文献[6]中证明的不等式
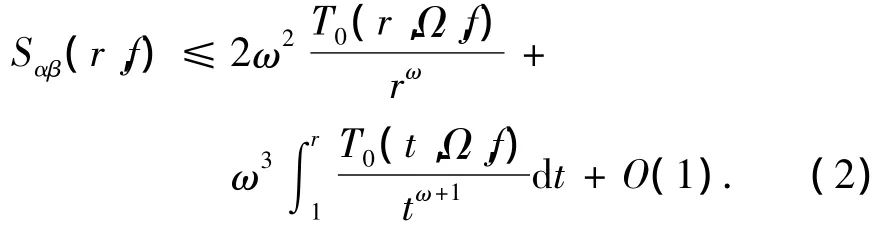
其中 Ω= Ω(α,β),ω= π(β - α),容易知道,若则σαβ(f)<∞.若{αj,βj}(j=1,2,…,q)为 q 组实数,满足

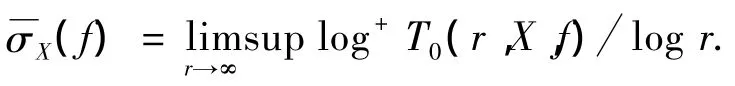
定理A[7]设A0(z)于开平面亚纯,具有非零的增长级ρ(0<ρ≤∞),其下级μ=μ(A0)<∞,在∞的亏量δ= δ(∞,A0)> 0.{αj,βj}(j=1,2,…,q)为满足(3)式的 q组实数,并且,其中σ > 0,μ≤σ≤ρ.若A(z)(j=j1,2,…,k)于开平面亚纯且 T(r,Aj)=o(T(r,A0)),则方程
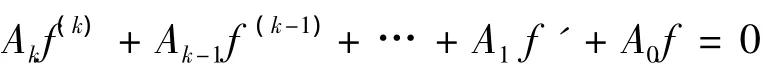
的每1个非零解f(z)有σX(f)=+∞,其中αj≤argz≤βj}.
自然会问:当A0(z)为具有有限亏值的亚纯函数时,方程(1)是否也有相同的结论?下面的定理回答了上述问题.
定理1 设A0(z)为ρ=ρ(A0)级亚纯函数,其下级μ=μ(A0)<∞,极点收敛指数λ=λ(1/A0)<ρ,存 在 有 限 亏 值 a,δ= δ(a,A0) > 0.{αj,βj}(j=1,2,…,q)为满足(3)式的 q组实数,令ω=max{π/(β1-α1),…,π/(βq-αq)},且ω<ρ,,其中 σ> 0,max{ω,μ,λ}< σ≤ρ.若Aj(z)(j=1,2,…,k-1)于开平面亚纯且ρ(Aj)=0,则方程

1 引理
为了证明定理,还需要下面的相关记号和引理.
引理1[8]设f(z)为角域上的有限ρ级亚纯函数,令 Γ={(n1,m1),(n2,m2),…,(nj,mj)}表示满足ni>mi≥0(i=1,2,…,j)的不同整数对的有限集合,设ε>0及δ>0为给定的正常数,则存在只与f,ε,δ有关的常数k>0,使得
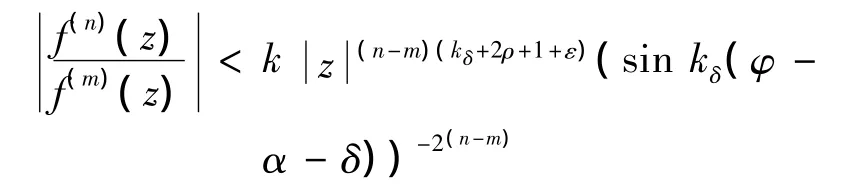
对所有(n,m)∈Γ 成立,其中z=reiφ∈Ω(α +δ,β-δ)且z∉D,D为由半径之和为有限的可数个圆盘构成的R-集,其中kδ=π/(β-α-2δ).
引理2[6,9]设f(z)为开平面上的超越亚纯函数,下级μ和级ρ分别满足μ<∞ 和0<ρ≤∞,则对任意满足μ≤σ≤ρ的正数σ和1个线性测度为有限的集合E,存在1个正数序列{rn}满足以下条件:
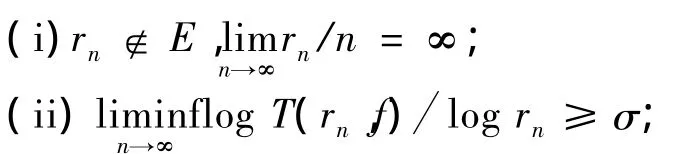
(iii)T(t,f)≤(1+o(1))(2t/rn)σT(rn/2,f),t∈[rn/n,nrn],并称满足上述条件的序列{rn}为f(z)在除集E外的σ级Pólya峰序列.
设f(z)为开平面上的亚纯函数,a为复常数,令
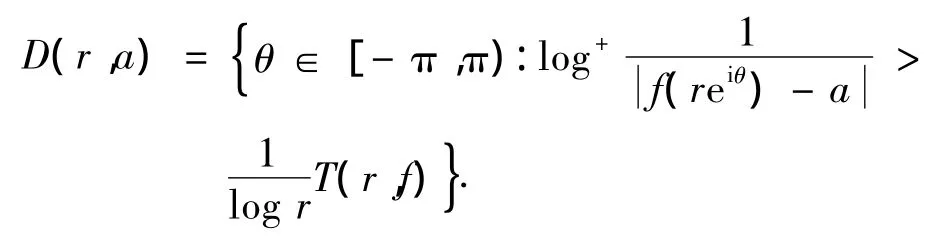
引理3[10]设f(z)为开平面上的超越亚纯函数,下级μ和级ρ分别满足μ<∞ 和0<ρ≤∞,若f(z)具有亏值a∈c^=c∪{∞},δ= δ(a,f)>0,则对f(z)的任一σ(μ≤σ≤ρ)级Pólya峰序列{rn}有
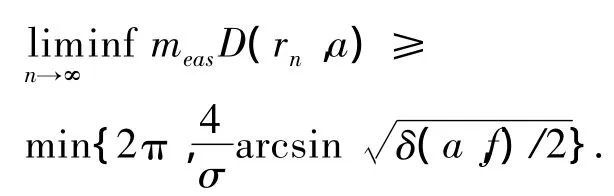
引理4[11]设f(z)为开平面上的亚纯函数,Ω(α,β)为开平面上的任一角域,0<β-α≤2π,则对任意复数a≠∞,有Sαβ(r,1/(f-a))=Sαβ(r,f)+ε(r,a),其中 ε(r,a)= Ο(1)(r→∞).
引理5[12]设f(z)为开平面上的亚纯函数,当f(0)≠∞时,
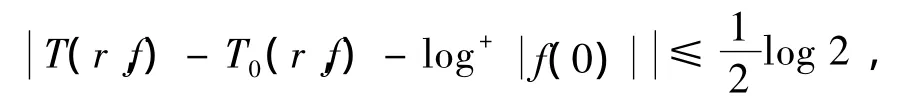
当f(0)=∞时,
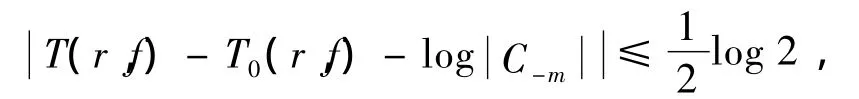
其中C-m表示f(z)在z=0点邻域内展式中的首项非零系数.
2 定理的证明
由方程(1)有

(i)若max{ω,μ,λ}<σ<ρ.
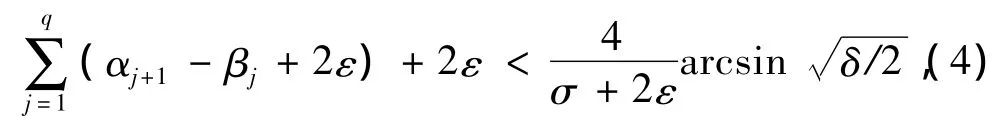
由引理1可知,对上述ε和对给定的ε0>0以及充分大的N,对每个j存在ηj满足
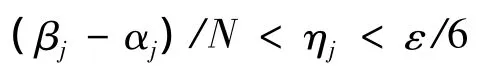
和只与 f,ε0,ηj有关的常数 h > 0,使得当 z=reiφ∈Ω(αj+ηj,βj-ηj),z∉ D 时,对所以的(n,m)∈ Γ有

其中kδ= π/(βj-αj-2ηj),D为引理1给出的R-集.
特别地,当z=reiφ∈Ω(αj+2ηj,βj-2ηj)时上式成立,且φ-αj-ηj>ηj>0,此时l(l为某一常数),所以当z=reiφ∈Ω(αj+2ηj,βj-2ηj),z∉D时,∃M > 0,不依赖z,使得

对A0(z)应用引理2,∃σ+2ε级Pólya峰序列{rn},使
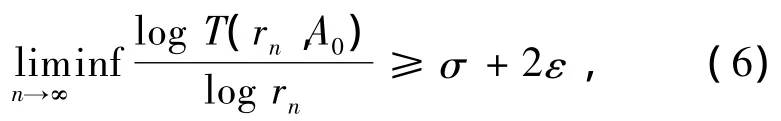
其中rn∉F.
由引理3,对充分大的n有
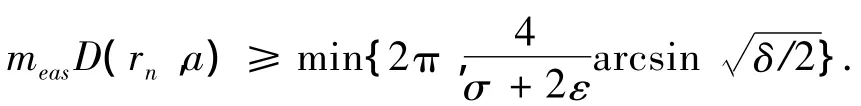
但由0<δ<1,1/2≤ω<σ可知,

则可得

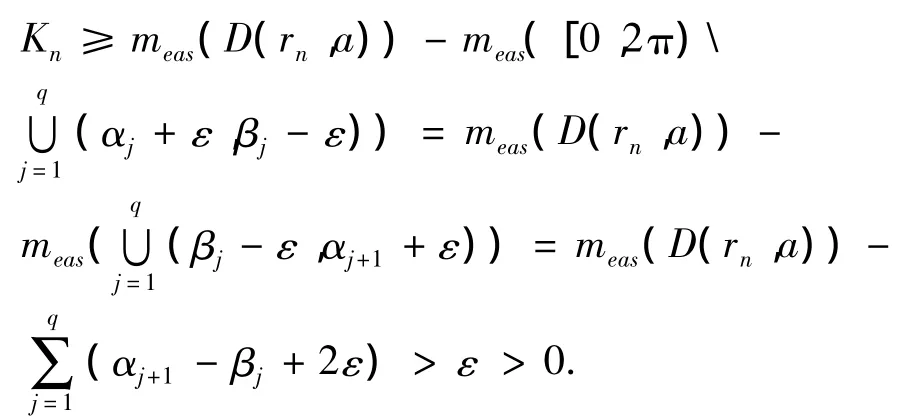

不妨设对所有n都成立,若不然只须取其子列代替.当n充分大时,有
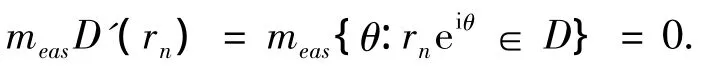
令 Dn=(αj0+ ε,βj0- ε)D'(rn),En=D(rn,a)∩ Dn,由 D(rn,a)的定义可知
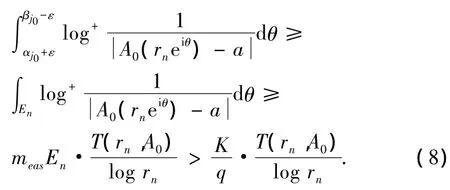
又设 B1:argz= αj0+ ε',B2:argz= βj0- ε'为由原点发出的2条半直线,当rn充分大时,取ε'∈(ε/3,2ε/3)使得B1,B2只与 D 中的有限个圆盘相交,令B2∩D},则measM1<+∞,measM2<+∞.
由 Bαβ(r,f)的定义可得
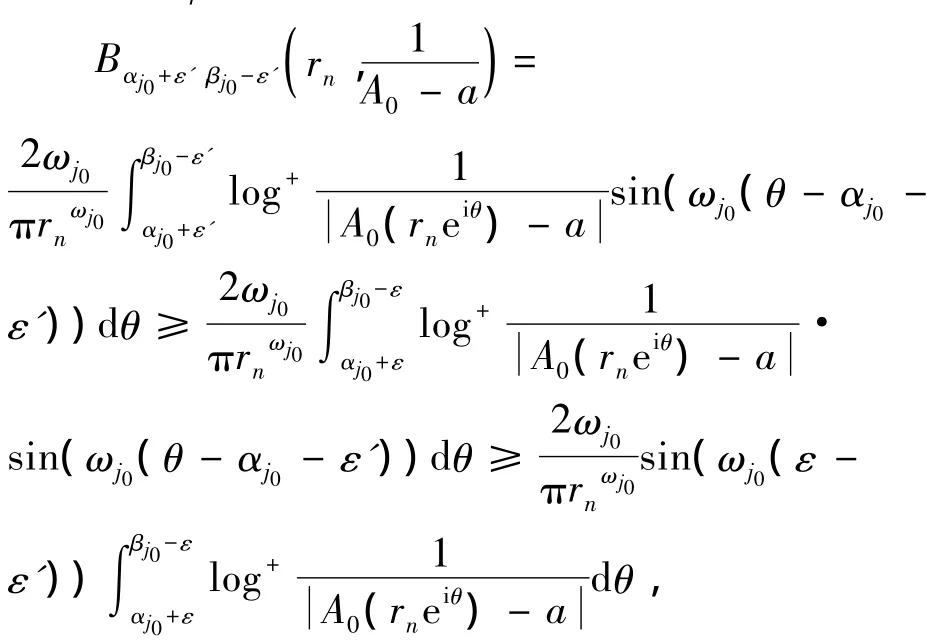
即得
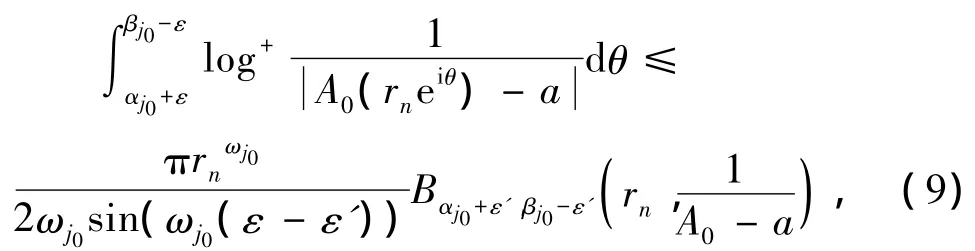
其中ωj0= π(βj0-αj0-2ε').
又由引理4可得

由rn∉F及B1,B2只与D中的有限个圆盘相交可得

又由于
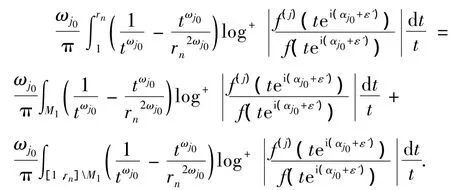
由(5)式,令 z=rei(αj0+ε'),当 r∈[1,rn]M1时,有
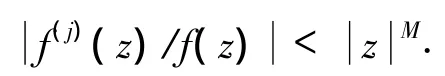
即可得

同理可得

即得

又由z=rneiθ∈Ω(αj0+ ε',βj0- ε')⊆Ω(αj+2ηj,βj-2ηj)可知,有,则可得Bαj0+ε',βj0-ε'(rn,f(j)/f)=O(1),即得
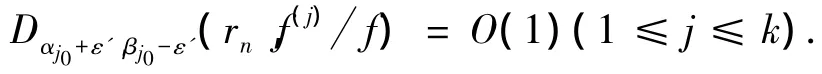
对Aj(z)(j=1,2,…,k)应用不等式(2)
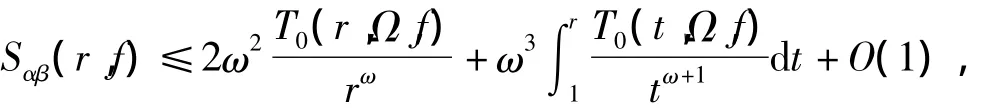
其中 Ω= Ω(αj0+ ε',βj0- ε'),ω= π/(βj0-αj0-2ε'),由引理5 可知 T0(r,f)=T(r,f)+O(1),则Dαj0+ε',βj0-ε'(rn,Aj)≤Sαj0+ε',βj0-ε'(rn,Aj)=O(T0(rn,Ω,Aj))=O(T0(rn,Aj))=O(T(rn,Aj)).
从而
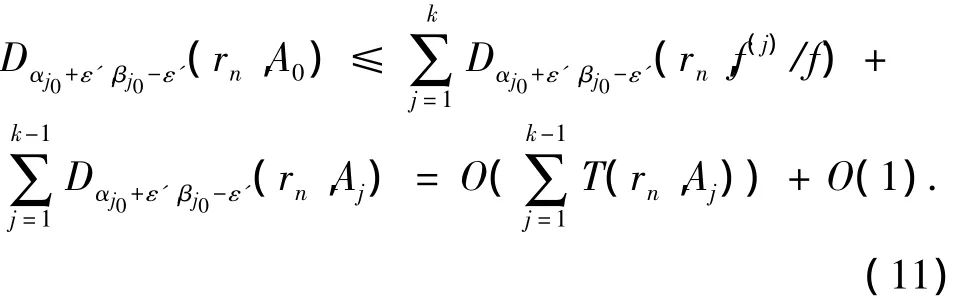

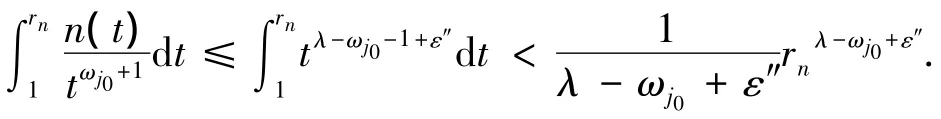
则
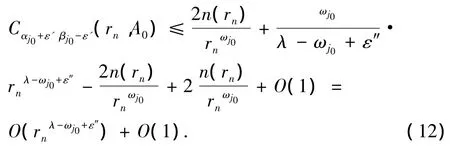
将(11)~(12)代入(10)式,再由(9)式可得
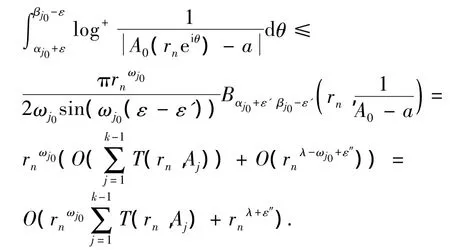
再联立(8)式可得

因
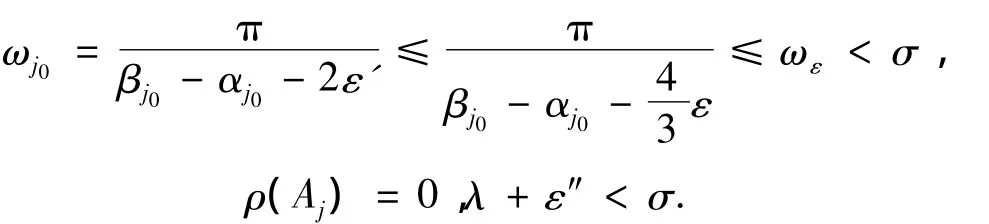
由(6)式及(13)式可得
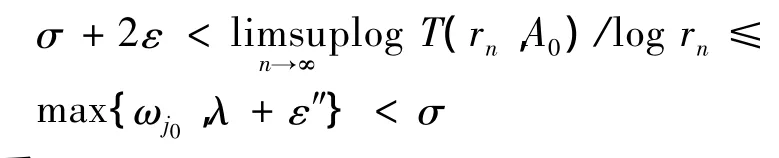
矛盾.
(ii)若σ=ρ时,对A0(z)应用引理2,存在σ级Pólya峰序列{rn},使
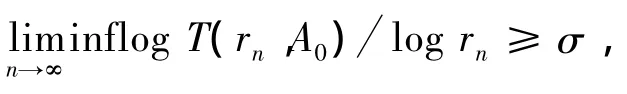
其中rn∉F.
在(4)式和(7)式处用σ代替σ+2ε,其余过程同(i)得σ<σ矛盾.故综合(i)、(ii),定理1得证.
关于方程的无穷级解的研究,还有许多有意义的结果.如文[13-14]等就是对方程的某些系数给定一定的条件,证明了方程的非零解为无穷级.
[1]Hayman W K.Meromorphic function[M].Oxford:Clarendon Press,1964.
[2]杨乐.值分布论及其新研究[M].北京:科学出版社,1982.
[3]GoldbergAA,OstrovskiiIV.The distribution of values ofmeromorphic functions[M].Russian:Izdat Nauk Moscow,1970.
[4]Nevannlinna R.Uber die eigenschaftenmeromorpher funktionen in einem winklraum[J].Acta Soc Sci Fenn,1925,50(12):1-45.
[5]Tsuji M.Potential theory inmodern function theory[M].Tokyo:Maruzen Co LTD,1959.
[6]Zheng Jianhua.Value Distribution ofmeromorphic Functions[M].Berlin:Springer-Verlag,2010.
[7]Wu Nan.Growth of solutions to higher order linear homogeneous differential equations in angular domains[J].Electronic Journal of Differential Equations,2010,164(1):1-7.
[8]Wu Shengjian.Estimates for thelogarithmic derivative of ameromorphic function in an angle and their application[C].Nankai:Proceeding ofInternational Conference on ComplexAnalysis at the NankaiInstitute of Mathematics,International,1992:235-241.
[9] Wu Shengjian.On transcendentalmeromorphic fuction with radially distributed values[J].China SerA Math,2004,47(3):401-416.
[10]BaersteinA.Proof of edrei’s spead conjecture[J].Proc London Math Soc,1973,26(3):418-434.
[11]Wu Shengjian.On the location of zeros of solution of f″+Af=0 whereA(z)is entire [J].Math Scand,1994,14(2):293-312.
[12]张广厚.整函数和亚纯函数理论[M].北京:科学出版社,1986.
[13]涂金,刘翠云,徐洪焱.亚纯函数相对于 φ(r)的[p,q]增长级[J].江西师范大学学报:自然科学版,2012,36(1):47-50.
[14]石磊,易才凤.一类高阶线性微分方程解的增长性[J].江西师范大学学报:自然科学版,2012,36(3):230-233.

