基于IRT模型的BP神经网络参数估计的进一步研究

关潮辉，丁树良

(江西师范大学计算机信息工程学院，江西南昌330022)

0 引言

项目反应理论(item response theory，IRT)是一种新兴的心理与教育测验理论，是在克服经典测验理论局限而产生和发展的［1］.参数估计是IRT的重要组成部分，但是由于IRT自身的复杂性，致使其相关模型的参数估计相对困难［2］.传统的参数估计方法要求测验的人数和题数都较大时才有较理想的分析结果.使用BP神经网络进行参数估计(BP降维法)［3-5］对考生人数、测验题数的要求较宽松且估计的精度较高.但是目前在设计网络结构时，网络隐层数及隐层节点数的确定还缺乏足够的理论指导，这使得网络结构的确定带有较大的主观性和艺术性［6-7］.本文主要对神经网络结构以及降维法进行改进，并达到了较好的效果.

1 研究方法

1.1 BP降维法

文献［4-5］提出BP神经网络降维法，采用BP神经网络与降维技术相结合，利用IRT中常用的联合似然估计思想进行参数估计［5］，用于处理各种IRT模型的参数估计，具有普遍适用性.本文主要讨论0-1评分的3参数逻辑斯蒂模型(3PLM):

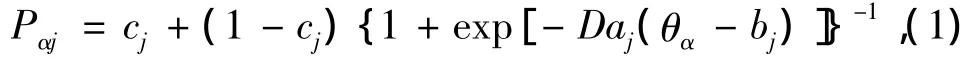
其中D=1.702 为常数，aj、bj、cj分别表示第i个题目的区分度、难度和猜测度，Pαj表示能力为θα的被试答对第 j题的概率［1］.

在文献［4-5］中BP神经网络使用Matlab神经网络工具箱来设计，采用4层神经网络，每层的节点数依次为10，7，3，1个，前3层采用 S型激活函数‘tansig’，最后一层采用线性激活函数‘purelin’，训练函数、学习函数采用默认方式，训练次数为100次.

根据Monte Carlo模拟生成的得分矩阵XN×M=(xij)进行降维.其中以被试i的平均得分作为该被试能力(θ)参数估计的输入;以题分对总分的相关系数作为题目参数区分度a的输入，以下si为第i个被试的总分，s-为N个被试的平均分，则

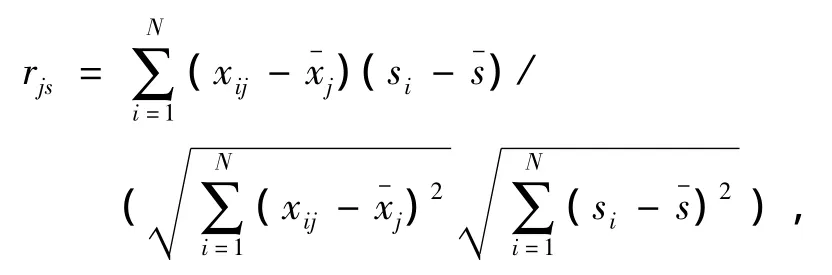
1.2 改进的BP降维法

在文献［4-5］提出的BP降维法中，BP神经网络的结构(4层，节点数分别为10，7，3，1)值得商榷.文献［8］指出，一个有3层单元的网络可以任意精度逼近任意函数.过多的层数不仅影响神经网络训练的速度，而且可能导致过拟合［9］，从而影响其泛化能力.通过凑试法［10］发现，采用新的神经网络结构，即2层神经网络，每层的节点数依次为3、1，前层采用“S”型激活函数‘tansig’，后层采用线性激活函数‘purelin’，训练函数采用‘trainbr’、学习函数采用默认方式，训练次数为100次.训练速度更快，且实验结果更好.

对于降维方法，文献［3］提出了不同的方法，在新的网络结构下，实验效果没有进一步稳定的提高，故还是沿用文献［4-5］的降维方法，但作必要的修正.当某题目所有被试均作答错误时，题目的区分度a对应的相关系数计算公式的分母为0.针对这一缺陷，本文提出修改，当第j题没人答对时，即得分阵XN×M的第 j列均为 0 时，有

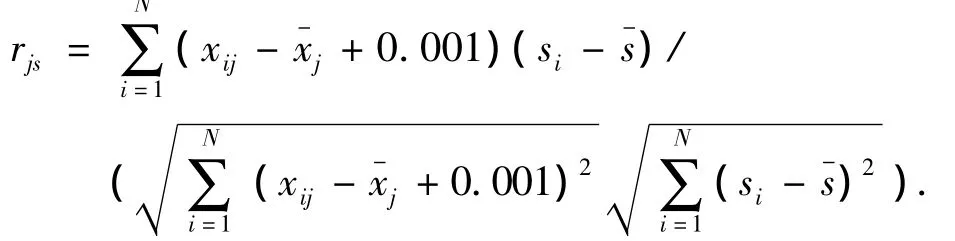
由于题目的通过率越高，题目相应的难度应该越小，采用通过率作为题目难度的输入从逻辑上看是不合理的.针对这一问题，以题目的未通过率=作为题目参数难度b的输入.对于猜测度c，当被试人数的尾数不为0时，l30不是整数，比如被试人数为45时，l30=13.5，与事实不符，故应该进行取整处理.

2 试验

蒙特卡洛模拟随机生成M个项目参数和N个被试能力参数，其中lna～N(1，0.4)(且0＜a≤2)，θ，b～N(0，1.5)(且 -3≤θ，b≤3)，c～β(3，30)(且0＜ c≤0.25).由(1)式计算Pαj，产生得分阵 XN×M=(xij)(rij～U(0，1)，rij≤Pαj，xij=1，否则xij=0)［4-5］. 重复生成RN×M=(rij)，产生30 个得分阵.采用上述的降维法以及修正后的降维法对得分阵进行降维，得出一行N列的向量(能力参数)或M行一列的向量(项目参数)作为30个神经网络的输入，以对应的能力参数或项目参数真值作为对应的输出，分别使用文献［4-5］的神经网络结构和新的神经网络结构训练神经网络.

模拟生成N1个被试能力参数，结合上述已经生成的M组项目参数，生成得分阵XN1×M，作为进行被试能力值的参数估计的测试样本.降维后生成输入向量，在原来训练好的30个网络上测试，以N1个被试能力为网络目标值，每次网络输出进行相加，循环.模拟生成M1组项目参数，结合上述已经生成的N个被试的能力参数，模拟生成得分阵XNXM，通过上述方法，同样可以完成项目参数估计.

使用估计值对真值的修复好坏的2个指标Abs和Rmasd作为评价估计好坏的标准［4-5］:

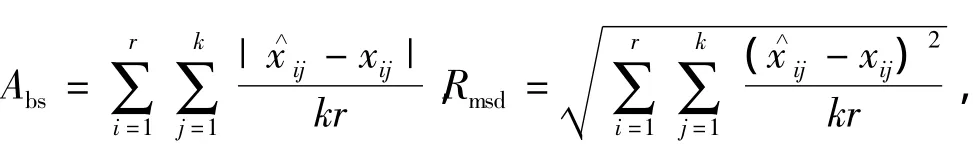
其中k，r表示待估参数个数和训练网络数，x∧ij表示参数的估算值，xij表示参数的真值.为了说明新的方法的时间效率有所提高，引入相对时间的概念:以新方法完成所有参数估计时程序的总耗时为一个单位时间，即T1=1，文献［4-5］的方法有T2=toldtnew，其中told表示文献［4-5］方法完成所有参数估计时程序的总耗时，tnew表示新方法的总耗时.

3 结果及其分析

令题数M=200，人数N=150，测试题数M1=50，测试人数N1=50，分别使用文献［4-5］的BP降维法和改进后的BP降维法进行试验，得到结果如表1所示.

表1 2种BP降维方法得到的各参数评价指标的比较

从表1可以看出，当训练人数N为150，训练题数M为200，施测题数或施测人数为50时，新法得到的各个参数的指标均优于文献［4-5］.其中，能力参数θ的Abs和 Rmsd，新法明显优于文献［4-5］.文献［4-5］的相对时间值为1.37，这相当于新法的程序运行的时间效率提高了近40%.

4 进一步的讨论

在研究过程中，发现存在以下问题值得进一步讨论:(i)当M≤8且N≤8，而M1或N1保持不变时，新方法的实验结果有时会比原来的方法差.事实上，当训练样本特别小的时候，是否还考虑使用降维法［4-5］，值得商榷.(ii)BP网络是目前使用最为广泛的神经网络之一，尽管如此，它仍存在网络易陷入局部极小、收敛速度慢、网络泛化能力差等不足［6］，如何结合神经网络集成法［7，11］，对其进行改进并应用于基于IRT的参数估计，值得研究.(iii)本文主要讨论的是BP神经网络，如果采用其他神经网络效果会如何?特别是BP神经网络是有监督的神经网络［10］，这大大限制了此类方法的实际应用.(iv)本文只讨论了基于简单IRT模型的参数估计，即0-1评分，单维的3PLM，如果采用多级评分或多维的IRT模型，该如何进行试验，值得讨论.

［1］漆书青，戴海琦，丁树良.现代教育与心理测量学原理［M］.北京:高等教育出版社，2002:80-96，97-142.

［2］ Baker F B.Item response theory:parameter estimation techniques［M］.2nd.New York:Marcel Dekker，Inc，2004:23-58，157-200.

［3］刘文，边玉芳，陈玲丽，等.BP神经网络估计IRT参数的比较研究［J］.中国考试，2013(2):7-11.

［4］谭云兰，丁树良，辛锐铭，等.基于IRT模型参数的BP神经网络估计［J］.计算机工程与应用，2004，40(17):56-57，108.

［5］谭云兰，丁树良，辛锐铭.基于IRT模型的BP神经网络降维法参数估计及其应用［J］.江西师范大学学报:自然科学版，2004，28(6):485-488.

［6］范佳妮，王振雷，钱锋.BP人工神经网络隐层结构设计的研究进展［J］.控制工程，2005，12(S1):105-109.

［7］余嘉元.基于神经网络集成的IRT参数估计［J］.江南大学学报:自然科学版，2009，8(5):505-508.

［8］Tom M M.机器学习［M］.曾华军，译.北京:机械工业出版社，2003:76-82.

［9］飞思科技产品研发中心.神经网络理论与MATLAB7实现［M］.北京:机械工业出版社，2005:68-69，107-113.

［10］ Hüsken M，Jin Y，Sendhoff B.Structure optimization of neural networks for evolutionary design optimization［J］.Soft Computing-A Fusion of Foundations，Methodologies andApplications，2005，9(1):21-28.

［11］周志华，陈世福.神经网络集成［J］.计算机学报，2002，25(1):1-8.