异常值对义务教育均衡发展程度评估的影响

钟 君，许志勇

(天津市教育招生考试院，天津300387)

0 引言

在国家大力推进义务教育均衡发展过程中，如何科学检验义务教育均衡建设成果、评估义务教育均衡发展成效是一个现实而重要的问题.这包含2个层面的内容:(i)建立全面反映均衡发展内涵的指标体系;(ii)确立科学测算均衡发展程度的方法.国内学者对此也开展了专门研究，如翟博等［1-3］从受教育机会、教育资源配置、教育过程和教育结果4个方面建立了评估指标，并主要采用了差异系数来测算教育均衡发展程度;傅禄建等［4］从资源配置、教育过程和办学质量3个方面构建了评估指标，并专门采用了基尼系数来研究教育均衡发展程度.此外，国家《县域义务教育均衡发展督导评估暂行办法》也采用了差异系数来评估县域内中小学校际均衡情况.

评估义务教育均衡发展程度，无论是采用差异系数法还是基尼系数法，均面临统计分析中一个无法回避的问题就是异常值的影响.这里的异常值不是指由于人工记录、数据录入等过失性错误导致的数据错误，而是指正确采集到的少数过大或过小的极端值.在我国现阶段义务教育校际差异、城乡差异和区域差异还比较明显的情况下，异常值的存在无法避免.但是在“办好每一所学校，教好每一个学生”的教育发展理念下，又必须关注每一所学校的数据，不应按照常规的统计分析程序清理掉异常值［5］.因此，在对义务教育发展具有重要导向作用的均衡发展程度评估中，不同的统计测算方法对异常值的敏感程度如何、异常值对评估结果有何影响，都是值得思考，并应审慎对待的问题.

1 义务教育均衡发展程度的测算方法

1.1 差异系数

差异系数(coefficient of variation)是一种描述数据离散程度的相对差异量数，指一组数据标准差与平均值的百分比，通常用CV表示.假设一组数据为 X1，X2，…，Xn，其平均值记为，标准差记为S，则这组数据差异系数的计算公式为

由于差异系数本身经过“均值化”的无量纲化处理［6］，不以原始数据的单位为单位，常用于2种测量单位不同或测量单位虽然相同但平均值相差很大的数据资料的差异情况的比较.差异系数大，表示数据分散范围广，参差不齐，差异较大;差异系数小，表示数据较为集中，变动范围小，差异较小.此外，差异系数的无量纲特性，特别适合多指标综合评价，利用多个单项指标评价结果合成综合评价结果.

正因为差异系数既能通过度量数据的离散程度来评价单项指标的均衡程度，又适合将多个单项指标评价结果合成综合评价结果，因此在义务教育均衡发展程度评估中得以采用.

1.2 基尼系数

基尼系数(gini coefficient)是意大利经济学家基尼(Corrado Gini)于1922年以洛伦兹曲线(Lorenz curve)为基础提出的，用于定量测定收入分配的差异程度.后来逐渐有学者将基尼系数从经济领域引入教育领域，开始用基尼系数分析研究教育问题，如张长征等［7］和孙百才［8］分别用基尼系数测算方法研究了我国改革开放后近二三十年的教育公平程度及教育平等问题.

洛伦兹曲线是经济学中用以描述社会收入分配状况的一种曲线，由累计的一定人口数量占总人口的百分比与这部分人口所获得的收入占总收入的百分比的对应关系来表示，如图1所示.

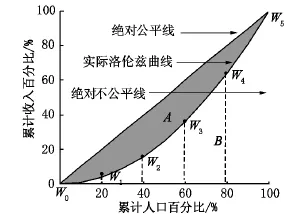
图1 洛伦兹曲线与收入不平等

基尼系数由图1中的绝对公平线和实际洛伦兹曲线围成的面积A与绝对公平线和绝对不公平线围成的面积A+B之比来测度.基尼系数通常用G表示，用公式表示为

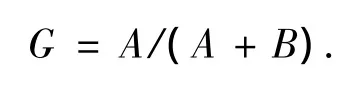
基尼系数取值范围为0～1，越接近0就表明收入分配越趋向平等，反之，收入分配越趋向不平等.基尼系数的计算方法很多，张建华［9］提出了一种简便易用的方法.假定全部人口平均分为n组，每组人口占全部人口的比例即为1/n，并假定以Wi表示从第1组直到第i组人口累计收入占全部人口总收入的百分比，则基尼系数的计算公式为

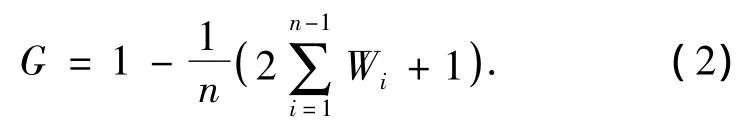
国际上通行的基尼系数计算，一般采用“五等份分组”法，即把全部人口平均分成5组，如图1所示.此时，基尼系数的计算公式为

2 异常值对义务教育均衡发展程度测算的影响

2.1 异常值的诊断

以《义务教育均衡发展程度测评:综合教育基尼系数方法》中，全部39所小学生均计算机台数为例［12］，利用拉依达准则，重复5遍剔除异常值的过程如表1所示.

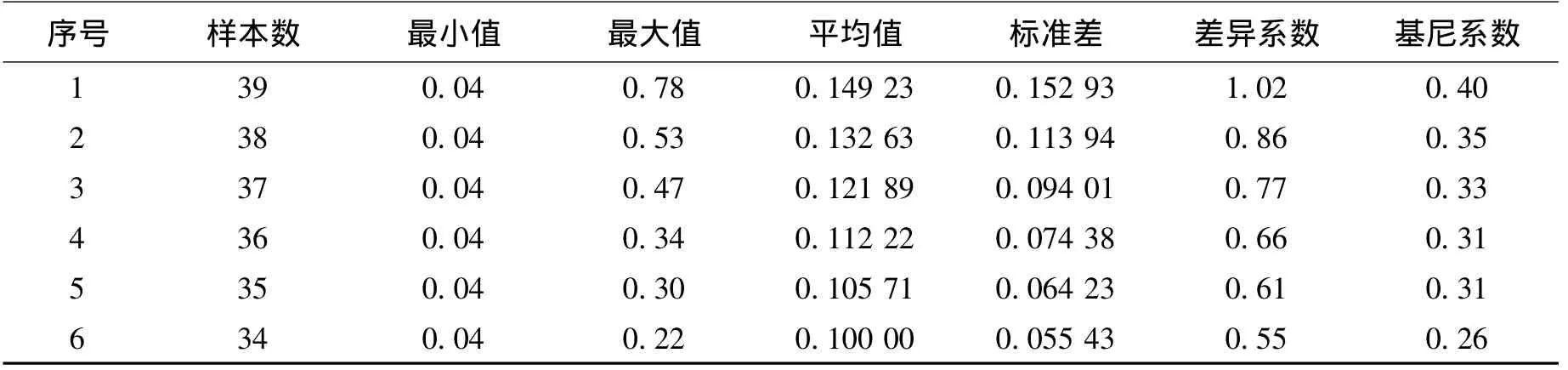
表1 生均计算机台数异常值剔除过程

由表1可以看出，随着异常值的逐个剔除，差异系数和基尼系数也逐渐减小，尤其是差异系数的减小程度明显高于基尼系数.采用拉依达准则剔除全部异常值后，差异系数比最初减小了约46%，基尼系数比最初减小了约35%.由此猜想，异常值对差异系数的影响程度高于基尼系数.

2.2 异常值对差异系数和基尼系数影响程度的模拟研究

在我国现实教育环境下，无论从教育资源配置，还是从办学质量来看，总体而言还是中等学校居多，待提高学校和优质学校相对少一些.鉴于此，为简便起见，这里假定评估指标数据服从正态分布，并在此基础上开展异常值对差异系数和基尼系数影响的模拟研究.

模拟研究的基本思路是:产生正态分布随机数，向其中掺加异常值，然后计算并分析差异系数和基尼系数的变化情况.

2.2.1 正态分布随机数的产生 假定正态分布的均值为μ，标准差为σ.当差异系数大于1/3时，即σ/μ＞1/3，此时μ-3σ＜0，产生随机数中出现负数的可能性就会增大，这与现实中各评估指标一般不会出现负值的情形不符.因此，在模拟研究中考虑2种情况:(i)当差异系数小于1/3时，直接产生正态分布随机数，这里取μ=10，σ=2;(ii)当差异系数大于1/3时，产生大于零的截尾正态分布随机数，这里取μ=10，σ=5.鉴于现实中一个区域内学校数量的有限性，这里分别考虑20所学校、50所学校、100所学校和200所学校的情况，并模拟产生相应数量的随机数.

2.2.2 异常值的产生 由于现实中异常值仅是少数，这里只在各种模拟情形下，逐步添加1～4个异常值进行模拟研究.但为避免异常值对原始随机样本的过大影响，控制异常值的数量不超过随机样本总量的10%，即在20所学校的情况，最多添加2个异常值.

(i)在μ=10，σ=2产生正态分布随机数的条件下，根据拉依达准则在(μ-5σ，μ-3σ)区间随机产生2个异常值，在(μ+3σ，μ+5σ)区间随机产生2个异常值.按照(μ-5σ，μ-3σ)区间异常值产生的先后顺序及(μ+3σ，μ+5σ)区间异常值产生的先后顺序，将2个区间中的异常值逐个交替添加到正态分布随机数中，即研究添加双侧异常值对差异系数和基尼系数的影响.

(ii)在μ=10，σ=5产生截尾正态分布随机数的条件下，根据拉依达准则，只在(μ+3σ，μ+5σ)区间随机产生4个异常值，以避免在(μ-5σ，μ-3σ)区间上产生负值，并将4个异常值按产生的先后顺序逐个添加到截尾正态分布随机数中，即研究添加单侧异常值对差异系数和基尼系数的影响.

每种情形经过20次模拟运算，计算得到差异系数和基尼系数的结果如表2所示.

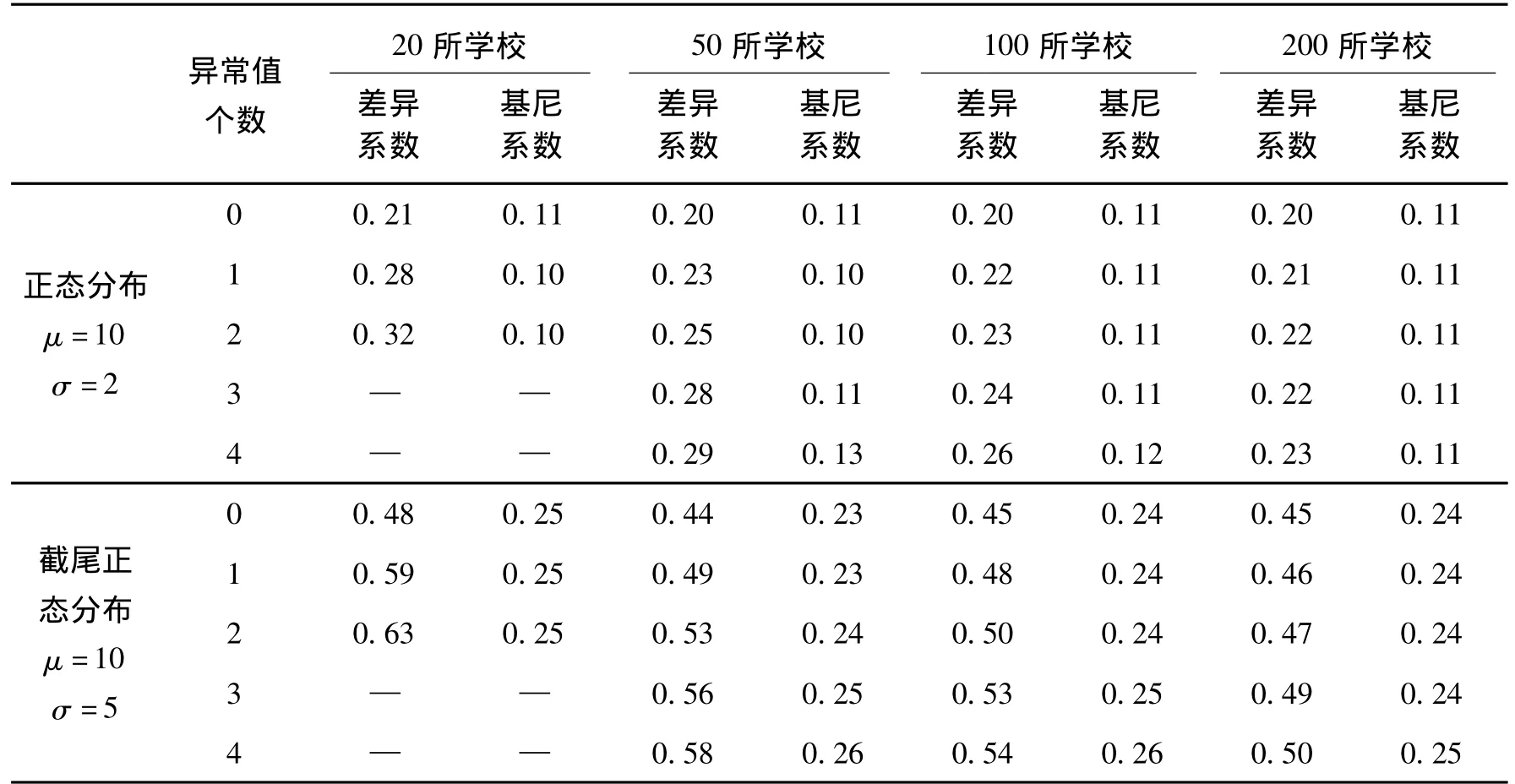
表2 模拟计算结果

3 讨论

差异系数和基尼系数是义务教育均衡发展程度评估2种常用的测算方法，本文通过向正态分布数据加入双侧异常值，以及向截尾正态分布数据加入单侧异常值进行模拟，研究结果表明:异常值对差异系数的影响程度明显高于基尼系数.但由于统计分布的多样性，若数据服从其他分布时，异常值对差异系数和基尼系数的影响如何，可参照此方法进一步研究.

此外，不同阶段我国义务教育均衡发展建设的重点可能不同，应根据不同测算方法的特点，选择适合评估目的的测算方法，以有利于达到促进义务教育高水平均衡发展的目的.

［1］翟博.教育均衡发展:理论、指标及测算方法［J］.教育研究，2006(3):16-28.

［2］翟博.中国基础教育均衡发展实证分析［J］.教育研究，2007(7):22-30.

［3］翟博，孙百才.中国基础教育均衡发展实证研究报告［J］.教育研究，2012(5):22-30.

［4］傅禄建，汤林春.义务教育均衡发展程度测评:综合教育基尼系数方法［M］.上海:华东师范大学出版社，2013:56-74.

［5］程开明.统计数据预处理的理论与方法述评［J］.统计与信息论坛，2007，22(6):98-103.

［6］张卫华，赵铭军.指标无量纲化方法对综合评价结果可靠性的影响及其实证分析［J］.统计与信息论坛，2005，20(3):33-36.

［7］张长征，郇志坚，李怀祖.中国教育公平程度实证研究:1978—2004——基于教育基尼系数的测算与分析［J］.清华大学教育研究，2006，27(2):10-14.

［8］孙百才.测度中国改革开放30年来的教育平等:基于教育基尼系数的实证分析［J］.教育研究，2009(1):12-18.

［9］张建华.一种简便易用的基尼系数计算方法［J］.山西农业大学学报:社会科学版，2007，6(3):275-283.

［10］何平.剔除测量数据中异常值的若干方法［J］.航空计测技术，1995，15(1):19-22.

［11］张敏，袁辉.拉依达(PaǔTa)准则与异常值剔除 ［J］.郑州工业大学学报，1997，18(1):84-88.

［12］傅禄建，汤林春.义务教育均衡发展程度测评:综合教育基尼系数方法［M］.上海:华东师范大学出版社，2013:87-89.