一类Markov-Feller算子不变测度的存在性与唯一性

郭新伟，吕延芳，齐海涛

(山东大学(威海)数学与统计学院，山东威海264209)

0 引言

Markov算子的遍历理论尤其是点态遍历定理的研究绝大多数都是考虑存在不变测度这一基本假设条件下展开的，因此Markov算子不变测度的存在性与唯一性一直是Markov过程的遍历理论研究的一个基本且重要的问题之一，它是进一步作渐近分析的基础.对于由紧空间上连续变换导出的Markov-Feller算子，文献［1］证明了此类算子存在唯一不变测度的充分必要条件，文献［2-4］分别利用Riesz表示定理和广义Farkas引理给出了局部紧的可分距离空间上的Markov-Feller算子存在不变测度的充分必要条件，文献［5］基于概率论中测度列的紧性概念，研究了完备可分距离空间上一类特殊的Markov算子即非扩张的Markov-Feller算子的渐近稳定性，文献［6］利用概率论中的鞅论方法证明了具有唯一不变测度的非扩张Markov算子轨道的稠密性质.对于比非扩张Markov算子更为一般的算子，如具有等度连续的对偶算子的Markov-Feller算子以及渐近强Feller算子，文献［7-8］分别给出了此类算子存在唯一不变测度的充分条件，此外文献［8］给出了该条件在随机2维Navier-Stokes方程中的应用.

本文将继续上述问题的研究，其主要目的是给出完备可分距离空间上具有等度连续的对偶算子的Markov-Feller算子存在不变测度以及唯一不变测度的条件，推广和改进了文献［6-7，9］的主要结果.

1 定义及其记号

设(X，ρ)是1个完备可分的距离空间，对任何X的子集A以及ε ＞0，用ρ(y，A)表示y到A的距离，Aε={y∈ X:ρ(y，A)＜ ε}，χA表示A 上的特征函数.

B(X)表 示 X 的 Borel σ-代数，(Msig(X)，‖·‖TV)表示(X，ρ)上的有限实值Borel符号测度全体组成的Banach空间，其范数‖·‖TV为通常的全变差范数.M(X)和M1(X)分别表示(X，ρ)上的有限实值Borel测度以及概率测度全体组成的Msig(X)的子空间.对μ∈M(X)，supp［μ］表示μ的拓扑子集［9］.(Bb(X)，‖·‖∞)表示X上的有界可测函数全体组成的Banach空间，其范数‖·‖∞为通常的上确界范数.Cb(X)表示X上的有界连续函数全体组成的Bb(X)的子空间.给定算子P:M(X)→M(X).若T满足下列2个条件:

(i)∀λ1，λ2∈ R+以及 μ1，μ2∈ M(X)，

P(λ1μ1+ λ2μ2)= λ1Pμ1+ λ2Pμ2;

(ii)∀μ ∈ M(X)，‖Pμ‖TV= ‖μ‖TV，即

P(μ(X))= μ(X)，则称P为Markov算子.

由符号测度的 Jordan分解定理，Msig(X)={μ1-μ2:μ1，μ2∈ M(X)}，因此，对 每 个 γ ∈Msig(X)，γ=μ1- μ2，令Pγ=Pμ1-Pμ2.易证P 是Msig(X)上的有界线性算子，且‖P‖≤1.因此，每个Markov算子都可以线性延拓到符号测度空间Msig(X)上.

∀f∈ Bb(X)，μ ∈ Msig(X)，记

对Markov算子P，若存在线性算子U:Bb(X)→Bb(X)，使得 ∀f∈ Bb(X)，μ ∈ M(X)，〈f，Pμ〉=〈Uf，μ〉，称U为 Markov算子 P的对偶算子.若U(Cb(X))⊂Cb(X)，则称P为Markov-Feller算子(或 Feller算子)，(U，P)为 Markov-Feller偶［10］.

给定1个映射π:X×B(X)→R，若π满足下列条件:

(ⅰ)对任意给定的 x∈ X，定义集映射 μx:B(X)→R，μx(A)= π(x，A)，∀A∈B(X)，其中μx是(X，ρ)上的Borel测度概率测度;

(ⅱ)对任意给定的A∈B(X)，定义函数gA:X→R，gA(x)= π(x，A)，∀x∈X，其中gA是(X，ρ)上的Borel可测函数，则称π是(X，ρ)(或X)上的1个转移概率或转移函数［7，11］.

设π是X上的1个转移概率.定义线性算子P:M(X)→M(X)以及U:Bb(X)→Bb(X)，P(μ(A))= ∫Xπ(x，A)dμ(x)，∀A ∈B(X)，μ ∈M(X)，

U(f(x))= ∫Xf(y)dπ(x，dy)，∀f∈ Bb(X)，易证(U，P)是Markov偶，称(U，P)是由转移π定义的Markov偶.若P为Markov-Feller算子，此时称π是X上的1个Feller转移函数.

设BL(X)表示X上的有界Lipschitz函数全体，对于f∈BL(X)，令‖f‖L表示f的(全局)Lipschitz常数，即，在BL(X)上定义范数‖·‖BL:

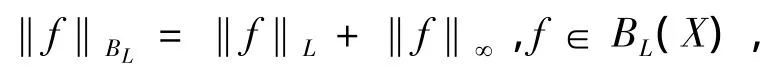
由文献［12］知，(BL(X)，‖·‖BL)是1个Banach空间.

由文献［13］知，在 Msig(X)上可赋予范数‖·‖，即对μ∈Msig(X)，

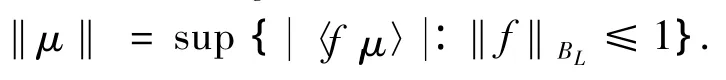
此外，在Msig(X)上也可以赋予下列Fortet-Mourier范数‖·‖F［6］:

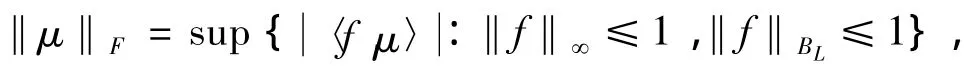
注意范数‖·‖和Fortet-Mourier范数是等价的.

给定测度序列{μn}⊂M(X)以及1个测度μ ⊂M(X)，若，则称{μn}弱收敛于μ.

实际上测度列的弱收敛即为{μn}(⊂M(X)⊂(X))按对偶空间(X)上的弱*拓扑收敛于μ.

关于测度的弱收敛，有下列结果.

定理1［14］测度序列{μn}弱收敛于μ的充分必要条件为{μn}依范数‖·‖收敛于μ，即

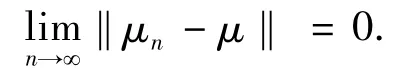
设P为 Markov-Feller算子，A∈ B(X)，使得U(χA(x))=χA(x)，则称A是P的不变集.设μ∈M1(X)，若Pμ=μ，则称μ是关于P不变的概率测度.若μ是关于P不变的概率测度，且对P的任一不变集A，μ(A)=0或μ(A)=1，则称μ是关于P遍历的概率测度.若P存在唯一的不变概率测度，则称P是唯一遍历的.

设A∈B(X)，若对P的任一不变的概率测度μ，μ(A)=1，则称A是极大概率集.

对每个f∈BL(X)，若函数列{Unf}限制在X中的每个紧集上是等度连续的，则称U是等度连续的.易证U是等度连续的充分必要条件是函数列{Unf}在X中的每一点都是等度连续的［10-11］.

关于 Markov算子的遍历理论，可参见文献［10-11，14］.

2 不变概率测度的存在性与唯一性

除非另有说明，以下均假设(X，ρ)是完备的可分距离空间，(U，P)是Markov-Feller偶，且U是等度连续的.令

定义下列集合:

Δt={μ∈M1(X):测度列{An(P)μ}是紧性测度列}，Γt={x∈ X:δx∈ Δt};

Δc={μ∈M1(X):测度列{An(P)μ}弱收敛}，Γc={x∈ X:δx∈ Δc}.

对x∈Γc，则测度列{An(P)δx}弱收敛于某个不变概率测度，记为εx.

在Γc上定义1个等价关系‘～’:对x，y∈Γc，x～y⇔εx= εy.

若x∈Γc，用［x］表示x所在的等价类，Γte={x∈ Γc:εx(［x］)=1}.

首先需要下列结果，其证明参见文献［15］.

引理1 Δt= Δc，Γt= Γc.

引理2 (i)Γte是闭的极大概率集，且是P-不变集;(ii)对每个x∈Γte，［x］是闭集.

引理3 μ是P的遍历概率测度的充分必要条件是∃x∈Γte，使得μ(［x］)=1，且在此种情形下，μ=εx.

此外，关于等度连续性，有下列结果.

引理4 U是等度连续的充分必要条件是P限制在(M1(X)，‖·‖)上是等度连续的.

证 充分性 若P限制在(M1(X)，‖·‖)上是等度连续的，从而对任意给定的x∈X，T在点δx∈M1(X)是等度连续的，所以任给的 ε＞0，∃δ1＞ 0，当‖μ -δx‖＜ δ1(μ∈M1(X))时，∀n∈N，

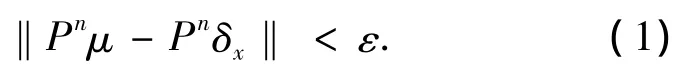
作映射 δ:(X，ρ)→(M1(X)，‖·‖)，δ(y)=δy，∀y∈X，则δ是连续的.因此，∃δ2＞ 0，当‖yx‖＜ δ2(y ∈ X)，‖δy- δx‖＜ δ1.

由(1)式知，∀n∈N，

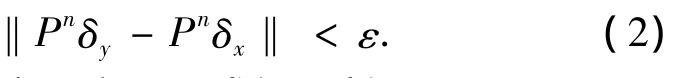
由范数‖·‖的定义和(2)式知，对任一g∈BL(X)，‖g‖BL≤1以及∀n∈N，

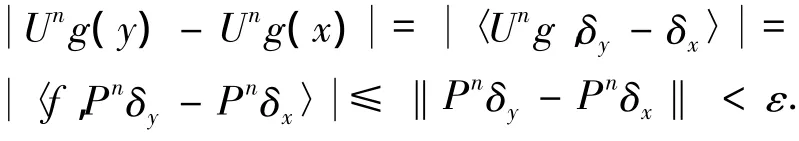
从而对任一g∈BL(X)，‖g‖BL≤1，{Ung}是等度连续的，由此可得:对任一f∈BL(X)，{Unf}是等度连续的，即U是等度连续的.

必要性若U是等度连续的，假设P限制在M1(X)上不是等度连续的，从而存在某个 μ0∈M1(X)，使得{Pn}在μ0处不是等度连续的，则存在某个ε0＞0及子列{rn}，以及μn∈M1(X)，

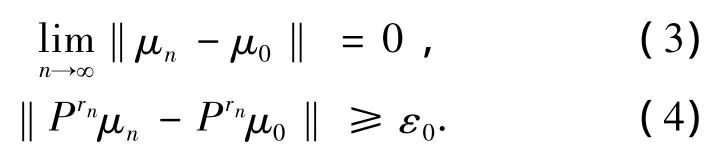
对任一g∈BL(X)，‖g‖BL≤1，{Ung}是一致有界且等度连续的函数列，由文献［13］及(3)式得

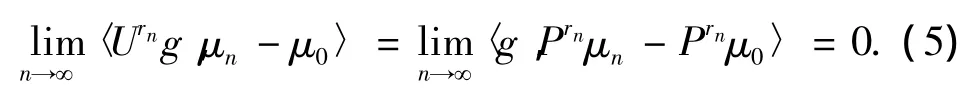
定理2 设(X，ρ)是完备的可分距离空间，P是X上Markov-Feller算子，若P有等度连续的对偶算子U，则下列条件等价:

(i)存在P的不变概率测度;

(ii)∃z∈X和x∈X，使得对z的任一开邻域B(z，δ)(δ＞ 0)，

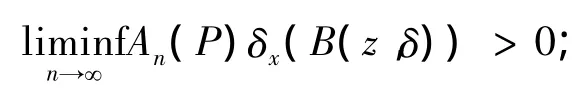
(iii)∃z∈X以及概率测度λ∈M1(X)，使得对z的任一开邻域 B(z，δ)(δ＞ 0)，

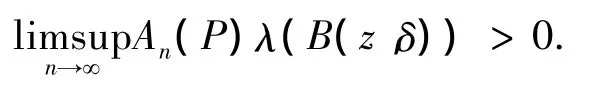
证(i)⇒(ii) 若存在P的不变概率测度，从而由遍历分解定理知，存在P的遍历测度［15］.记μ为P的遍历测度.由引理3知，∃x∈Γte，使得μ=εx.取z∈supp［μ］，由εx的定义由Portmanteau定理知，对z的任一开邻域B(z，δ)，

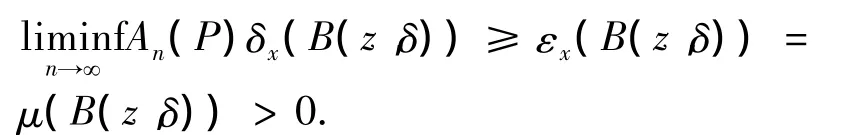
(ii)⇒(iii)取λ=δx.

(iii)⇒(i)假设z∉Γc=Γt，由文献［7，16］知，对某个0＜ε0＜1/2，存在子列{tn}以及X中的紧集列

由引理4，P限制在(M1(X)，‖·‖)上是等度连续的，因此，∃δ0＞ 0，使得对任一 y∈ B(z，δ0)，

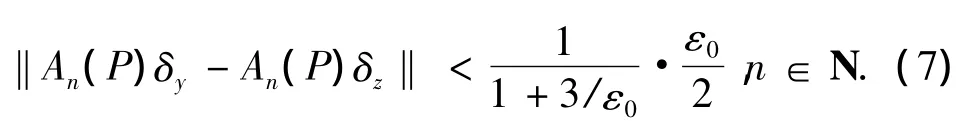
令 gn(x)=0∨(1- ε0ρ(x，Kn)/3)，则 χKn≤从而由(6)式和(7)式，对任一 y ∈ B(z，δ0)，

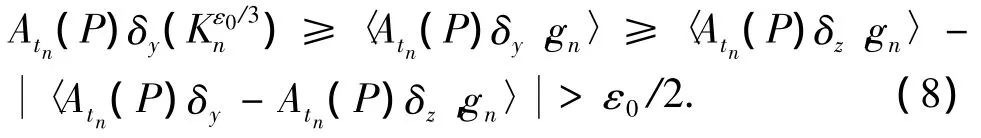
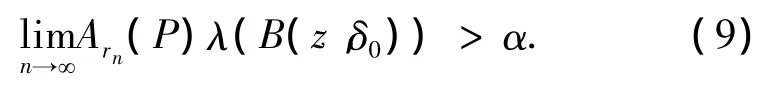
对任一n∈N，由(8)式得

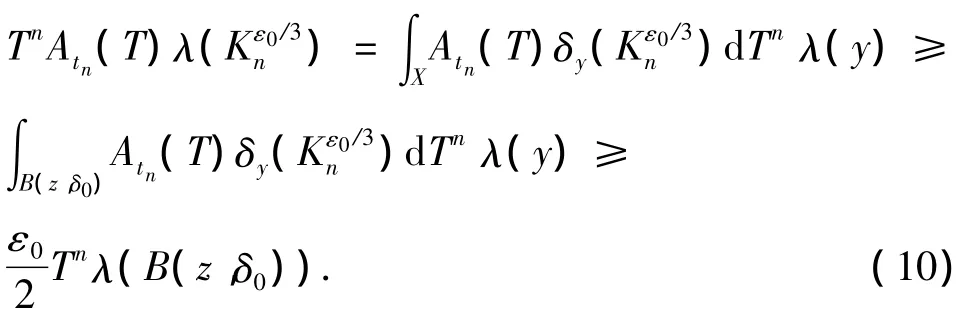
由于

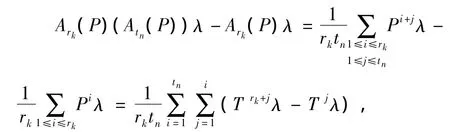
所以

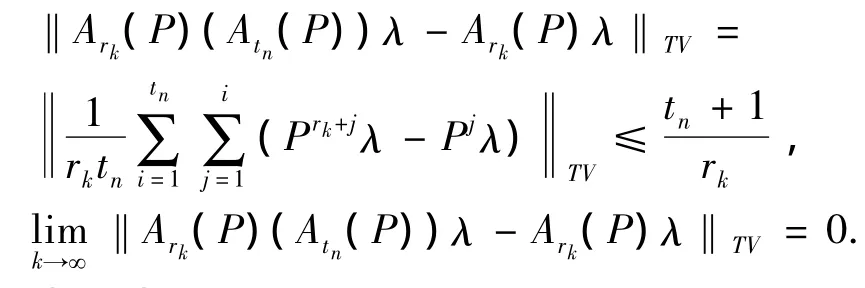
由上式得

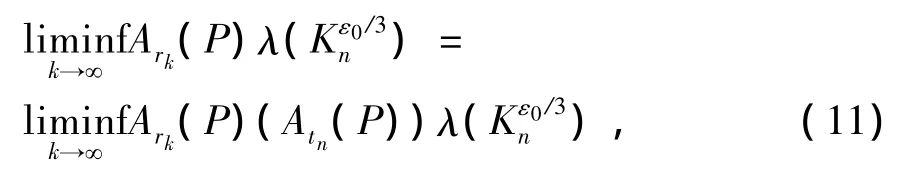
从而由(9)式和(10)式得

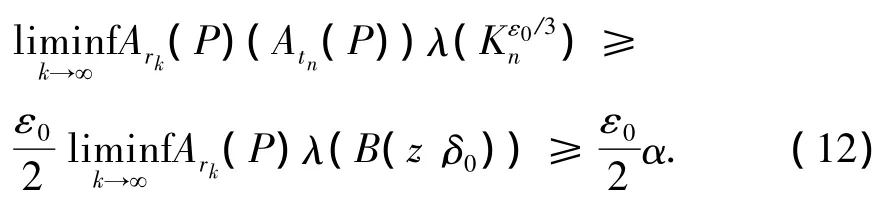
由于 n≠m，Kε0/3n∩ Kε0/3m= ∅(n，m ∈ N)，由(11)式和(12)式得，对任一m∈N，

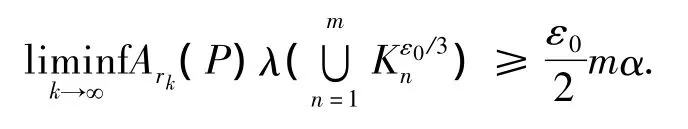
上式不可能对一切的m∈N成立，与假设z∉Γc= Γt矛盾.从而z∈Γc= Γt.由Γc的定义，φz是T的不变概率测度.

注意在定理2 的(iii)⇒(i)证明过程中仅用到了对每个f∈BL(X)，{Unf}在点z的等度连续性即{Tnδx}在点z的等度连续性，从而证明了

推论1 设(X，ρ)是完备的可分距离空间，(U，P)是Markov-Feller偶.若∃z∈X，使得{Unf}在点z是等度连续的，则存在P的不变概率测度的充分必要条件是下列条件之一成立:

(i)∃x∈ X，使得对 z的任一开邻域 B(z，δ)(δ ＞ 0)

(ii)存在1个概率测度λ∈M1(X)，使得对z的任一开邻域 B(z，δ)(δ＞ 0)，

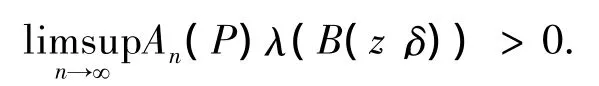
特别地，若λ=δx，推论1就是文献［9］的命题2.1.因此，推论1将文献［9］的命题2.1中的特殊单点测度推广为一般的概率测度以及上极限改进为下极限.

下面讨论Markov-Feller的不变测度的唯一性.为此需要下列定义［7］.

设P:M(X)→M(X)是1个Markov算子，若对任一 x，y∈ X，∃n0∈ N，使得

则称T有相交支集.

关于Markov-Feller的不变测度的唯一性，有下列结果.

定理3 设(X，ρ)是完备的可分距离空间，P是X上Markov-Feller算子，且P有等度连续的对偶算子U.若对任一x，y∈X，∃z∈X，使得对每个δ＞ 0，∃n1，n2∈ N，使得

则P至多有1个不变概率测度.

证若P至少有2个不变概率测度，则P至少有2 个遍历的概率测度εx，εy，此处x，y∈Γte且x≠y，由已知条件得∃z∈X，使得对每个δ＞0，∃n1，n2∈ N，使 Pn1δx(B(z，δ)) ＞ 0，Pn2δy(B(z，δ)) ＞0，从而

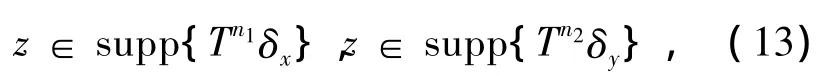
由于 x，y ∈ Γte且 εx≠ εy，所以

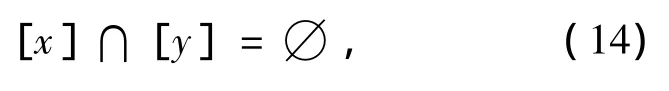
而εx［x］=1，εy［y］=1 且［x］和［y］为闭集，所以

显然supp{δx}⊂supp{εx}⊂［x］，supp{δy}⊂supp{εy}⊂［y］，由文献［10］得

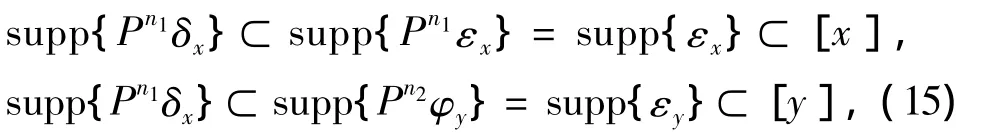
从而结合(13)式和(15)式得z∈supp{Tn1δx}∩ supp{Tn2δy}⊂［x］∩［y］= ∅.与(14)式矛盾.因此，P至多有1个不变概率测度.

特别地，在定理3中，若n1=n2，则推得到下列结果.

推论2 设(X，ρ)是完备的可分距离空间，P是X上Markov-Feller算子，且P有等度连续的对偶算子U;若P有相交支集，则P至多有1个不变概率测度.

设(U，P)是由转移函数 π定义的 Markov-Feller算子偶，由文献［17］知，对任一μ∈M1(X)，存在 1个概率空间(Ω，F，Prob)以及 Markov链{xn}n≥0，使得

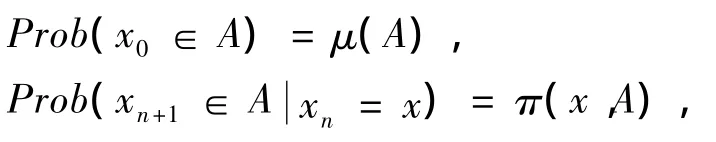
称 Markov链{xn}n≥0为对应于 P的 Markov链{xn}n≥0.

关于具有等度连续的Markov-Feller算子的轨道性质，有下列结果.

定理4 设(U，P)是由转移函数π定义的Markov-Feller偶且U是等度连续的.假设P存在遍历的不变概率测度μ.令A*=supp［μ］，{xn}n≥0是对应于P的Markov链.若Prob(x0∈A*)=1，则

证因为μ是T的遍历测度，所以由引理3知，∃x∈ Γte，使得 μ(［x］)=1，且 μ= εx.由于A*=supp［μ］，而［x］为闭集，所以A*⊂［x］.对任一y∈A*⊂［x］，则x～y.由定义知，

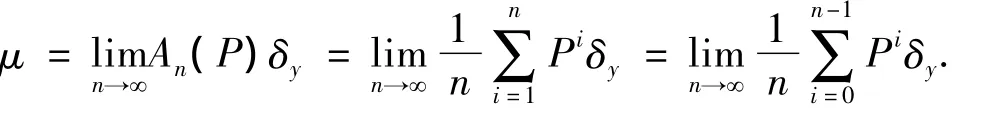
对A*中任一开集U，由Portmanteau定理得

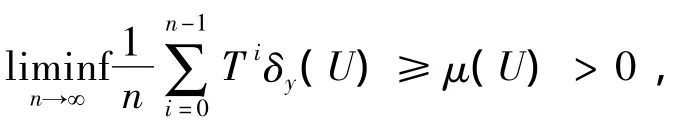
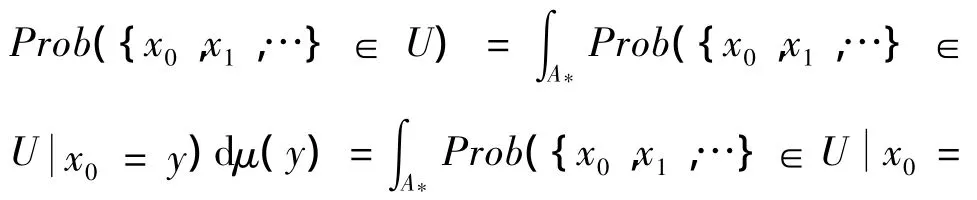
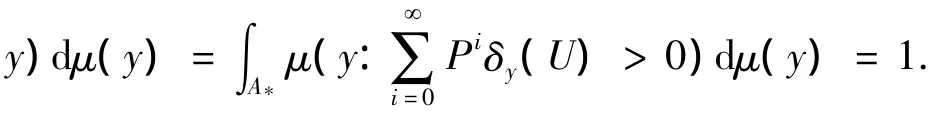
若满足下列条件:‖Tμ1-Tμ2‖F≤‖μ1- μ2‖F，∀μ1，μ2∈ M(X)，则称T是非扩张的.

推论3 设P是非扩张的Markov-Feller算子.假设P存在唯一不变的概率测度 μ.令A*=supp［μ］，{xn}n≥0是对应于 P 的 Markov 链. 若Prob(x0∈A*)=1，则

证若P是非扩张的，因此，对任一n∈N，

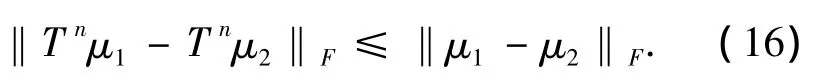
由于M(X)上的范数‖·‖F和‖·‖是等价的，从而由(16)式知P是等度连续的.因此，由引理4知，U是等度连续的.

又因为μ是T的唯一不变的概率测度，从而μ是遍历的.由定理4 知

推论3即是文献［6］中的定理3.2.因此，定理4是对文献［6］中定理3.2的改进和加强，并且与文献［6］所用的鞅定理的证明方法不同.

［1］Walters P.An introduction to Ergodic theory［M］.Berlin:Springer-Verlag，2003:146-153.

［2］王明文.一类Markov过程不变测度的存在性及应用［J］.江西师范大学学报:自然科学版，1991，15(4):306-312.

［3］Lasserre J B.Invariant probabilities for Markov chains on ametric space ［J］.Stat Probab Lett，1997，34(3):259-265.

［4］ Lasserre J B.Existence and uniqueness of an invariant probability for a class of Feller-Markov chains［J］.Theoret Probab，1996，9(3):595-612.

［5］ Szarek T.The stability of Markov operators on Polish spaces［J］.Stud Math，2000，143(2):145-152.

［6］ LastoA，Myjak J，Szarek T.Markov operators with a unique invariantmeasure ［J］.J MathAnalApp，2002，276(1):343-356.

［7］Szarek T.The uniqueness of invariantmeasures for Markov operators［J］.Stud Math，2008，189(3):225-233.

［8］Hairer M，Mattingly J.Ergodicity of the 2D Navier-Stokes equations with degenerate stochastic foring ［J］.Ana Math，2006，164(3):992-1032.

［9］Szarek T.Feller processes on nonlocally compact spaces［J］.TheAnnals of Probability，2006，34(5):1849-1863.

［10］Zaharopol R.Invariant probabilities of Markov-Feller operators and their supports［M］.Basel:Birkhǎuser-Verlag，2005.

［11］Lemma O H，Lasserre J B.Markov chain and invariant probabilities［M］.Basel:Birkǎuser-Verlag，2003.

［12］Weaver N.Lipschitz algebras［M］.New York:World Scientific Publishing Co Pte Ltd，1999.

［13］Dudley R M.Real analysis and probability［M］.Beijing:China Machine Press，2006.

［14］ Fougel S R.The Erdodic theory of Markov processes［M］.New York:Vas Nostrand Reihold Co，1969.

［15］郭新伟，喻建华，齐海涛.一类 Markov的遍历性［J］.江西师范大学学报:自然科学版，2013，37(2):183-186.

［16］Ethier S N，Kurtz T G.Markov process characterization and convergence［M］.New York:John Wiley ＆ Sons，1983.

［17］Meyn S P，Tweedie R L.Markovchains and stochastic stability［M］.Berlin:Springer-Verlag，1993.