有界闭区域中的随机取点方法及Mathematica 软件实现
2014-01-20 03:24王晓刚李德才
扬州职业大学学报 2014年2期
王晓刚,李德才
(扬州职业大学,江苏 扬州 225009)
地质勘探、环境监测等工程应用领域中,经常需要在一个有界闭区域中按随机抽样原则随机取点。所谓简单随机抽样原则,就是对于该区域的一个子区域D1而言,所抽到的点落在D1中的概率仅与D1的测度有关,而与所处位置与形状无关。
1 基础理论

其中,变量X 的边缘概率密度是
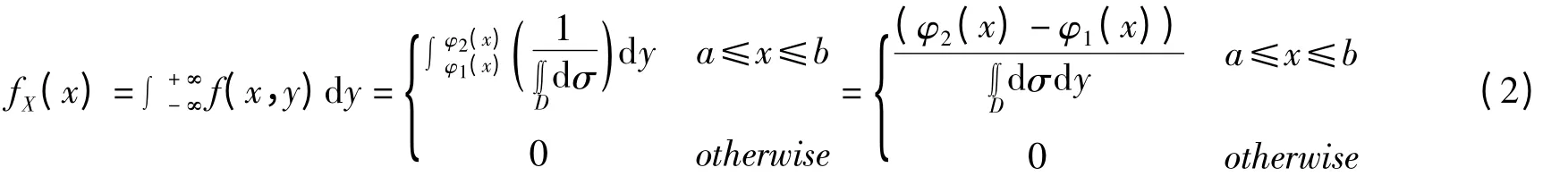
记随机函数的返回值为ξ,则ξ 服从区间[0,1]上的均匀分布,概率密度是

设g 从ξ 到X 的映射X=g(ξ),其中g 单调递增可微,则fξ(g-1(x))·(g-1(x))' =fX(x)且g(0)=a,g(1)=b,解得

由ξ 值利用式(4)解出X 值,Y 在X 取定后的条件分布是区间[φ1(X),φ2(X)]上的均匀分布,再次利用随机函数得到一个返回值η,可按照式(5)所示的线性变换得到Y 值。[1]

2 应用实例
其次,再次利用随机数函数Random[]返回一个[0,1]间的随机数,作为η 的赋值,假设操作结果是η=0.3328,利用式(5)得到相应的Y 值为Y = - 0.3338,从而得到区域D 内任一点(0.3328,-0.3338)。
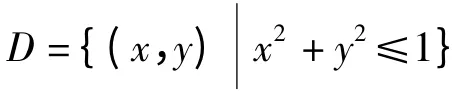
3 三维拓展
下面以一个实例说明如何利用随机函数Random[]在三维有界区域中随机取点。
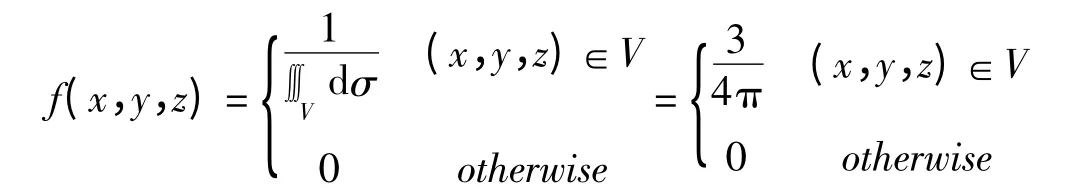
将区域V 表示成
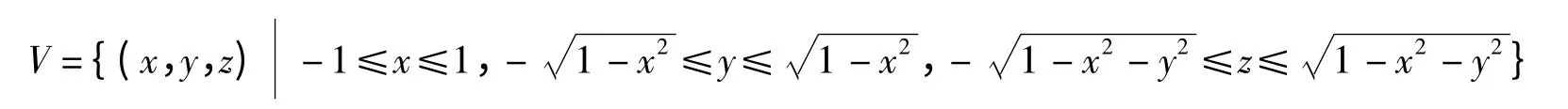
其中,变量X 的边缘概率密度函数是
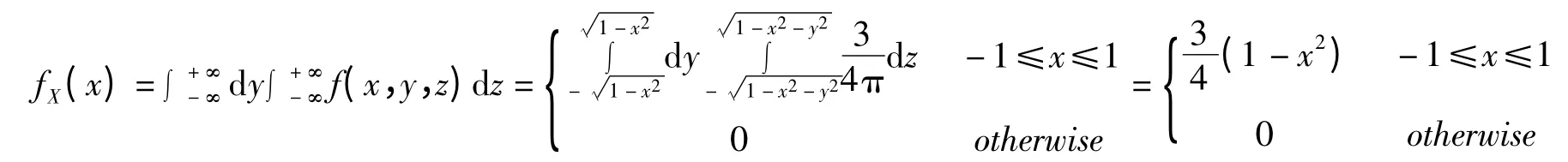
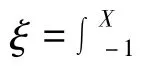
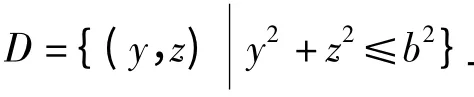
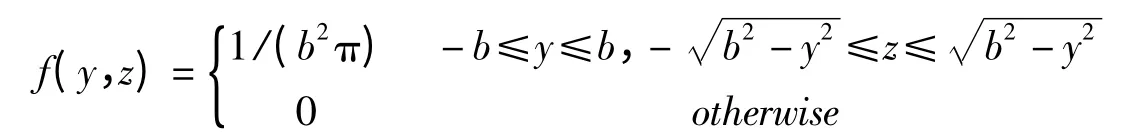
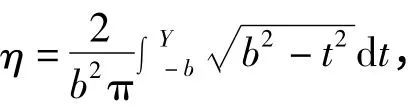
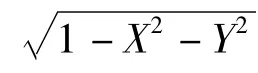
[1] 盛骤,谢式千.概率论与数理统计[M].北京:高等教育出版社,2001.
[2] 张宝善.Mathematica 符号运算与数学实验[M].南京:南京大学出版社,2007.
猜你喜欢
延安大学学报(自然科学版)(2020年4期)2021-01-15
数学学习与研究(2020年15期)2020-11-28
河北建筑工程学院学报(2020年4期)2020-04-29
数学物理学报(2019年3期)2019-07-23
物理与工程(2019年1期)2019-03-22
中学生数理化·高二版(2017年3期)2017-07-07
电脑知识与技术(2016年31期)2017-02-27
福建中学数学(2016年4期)2016-10-19
建材发展导向(2016年3期)2016-05-23
振动工程学报(2015年2期)2015-03-01

