边坡失效概率估计的高斯过程动态响应面法

苏国韶，赵 伟，彭立锋，燕柳斌

（广西大学 土木建筑工程学院 工程防灾与结构安全教育部重点实验室，南宁 530004）

1 引 言

边坡可靠性研究是当前岩土工程界的研究热点之一[1]。复杂边坡工程的可靠性分析中，其功能函数一般是隐式的，这给常用的一次二阶矩法（FORM）、二次二阶矩法（SORM）、直接积分法等带来了困难，直接蒙特卡罗模拟方法（MCS）适用于求解隐式功能函数的可靠性问题，且计算精度较高，但为了保证计算精度，MCS 法要求的抽样次数很大，尤其是对于功能函数值需要借助于计算耗时的有限元获取时，大量的重分析导致计算量巨大，从而导致MCS 法在工程应用中受到了极大限制。

利用少量的采样点，采用二次多项式的经典响应面（RSM）[2]、人工神经网络（ANN）[3]、径向基函数（RBF）[4]、克里金（Kriging）[5]以及支持向量机（SVM）[6]等回归工具构建隐式功能函数的响应面，然后结合FORM、SORM 及MCS 等常规方法进行可靠性分析，可有效降低结构重分析次数，显著提升计算效率，目前已成为复杂边坡可靠性分析的重要途径。但这类响应面方法仍存在着诸多问题需要解决：①二次多项式难以逼近高度非线性的功能函数，导致计算误差较大；ANN、RBF 等存在着小样本问题推广能力欠佳和过度拟合等瓶颈问题[7]；SVM 存在着合理核函数及其参数难以确定的公开问题[6]，为此有必要探求采用回归性能更好的回归工具，实现高度非线性隐式功能函数的高精度重构。②当功能函数非线性较高时，采用FORM、SORM 法往往难以收敛或获得合理的验算点，这必将导致基于FORM 或SORM 的响应面方法计算误差较大[8－9]，MCS 方法无需计算验算点，对求解功能函数呈高度非线性的可靠性问题具有较强的适应性，为此有必要探求新的基于MCS 法的响应面方法。③现有的基于 MCS 的响应面方法如ANN-MCS[3]、RBF-MCS[4]、SVM-MCS[10]等存在着过度依赖预设样本的规模与分布的瓶颈问题。为了降低计算代价，此类方法一般采用试验设计方法构建少量的预设样本，且仅利用一次构建的预设样本来构造响应面。一旦预设样本过少或空间分布不合理或外推预测样本远离预设样本空间时，响应面的重构精度就难以保证，为此有必要在计算中引入响应面动态更新的机制，以有效降低可靠性分析方法对预设采样点的依赖性。

高斯过程是新近发展起来的一种机器学习模型[11]，可分为高斯过程分类与高斯过程回归（Gaussian process regression，GPR）两种模型，它有严格的统计学习理论基础，对于处理高维数、小样本、非线性等复杂回归问题具有良好的适应性，在诸多领域中得到了广泛应用[12－14]。值得指出的是，与ANN、SVR 等常用的机器学习模型相比较，GPR 的优势主要体现在可给出具有概率意义的回归结果以及模型最优超参数可自适应获取。

本文提出一种边坡失效概率快速估计的高斯过程动态响应面法，该方法利用GPR 模型实现小样本条件下非线性隐式功能函数的高精度逼近，通过迭代计算构建一种GPR 响应面拟合误差的快速缩减机制，从而实现响应面拟合精度的自适应提高，进而结合MCS 法计算边坡的失效概率，为高效快速地求解边坡的失效概率提供新的途径。

2 高斯过程回归

从统计学的角度来看，GPR是这样的一个随机过程：其任意有限变量集合的分布都是高斯分布，即对任意整数n≥1 及任意的一族随机变量x，与其对应的t时刻的过程状态f(x)的联合概率分布服从n维高斯分布。GPR 的全部统计特征完全由它的均值和协方差函数来确定。

假设有n个观察数据的训练集D={(xi,yi)|i=1,…}n，xi为d 维输入矢量，观察目标值yi∈R 。如果X 表示d×n 维输入矩阵，y 表示输出矢量，那么训练集 D=(X,y)。

对于新的输入X*，GPR 模型的任务是根据先验知识预测出与X*相对应的输出值 y*。

带高斯噪声ε 的标准线性回归模型为

式中：f(X)为回归函数值；ε的各元素均为符合高斯分布的独立随机变量，均值为0，方差为。

观察目标值y 的先验分布为

式中：I为单位矩阵；K=K(X,X)为n×n阶对称正定的协方差矩阵，矩阵中的任一项 kij度量了xi和xj的相关性。

n个训练样本的观察目标值y 和m个测试样本的回归函数输出f*所形成的联合高斯先验分布为

式中：K(X,X*)为测试点 X*与训练集的所有输入点X 的n×m阶协方差矩阵，可简写为K(X*)；k(X*,X*)为测试点X*自身的m×m协方差矩阵，可简写为 k(X*)。

GPR 模型常用的协方差函数为

式中的最优超参数θ=(l,σf,σn)可通过极大似然法自适应获得，对数似然函数的形式为

对训练集进行学习，根据贝叶斯原理，利用观察到的真实数据不断更新概率预测分布，即给定测试点X*、训练集的输入值X 和观察目标值y 的条件下，推断出 f*的最大可能的预测分布为

其中：预测分布的均值和方差为

GPR 模型是一个具有概率预测意义的模型，它能将认知的先验信息和样本信息有效结合并以概率分布的形式描述不确定性。不仅可以给出预测变量的均值，还能给出其方差和指定概率的置信区间，描述变量发生的不确定性程度。GPR 模型的最大特色之一在于以概率分布的形式描述预测结果，利用GRP 模型提供的预测方差，能十分方便地对回归与外推预测结果进行不确定性评价。

下面用一个函数回归的例子来说明GPR 模型的不确定性评价功能。假设回归的目标函数为y=0.5sin(2x)，根据该式随机构造考虑噪音腐蚀条件下x∈[-2.5，2.5]的10个学习样本，利用学习样本建立GPR 模型，然后利用GPR 模型对x∈[-3，3]区间函数曲线进行预测，预测效果见图1，图中的灰色条带区域表示为置信水平为95%的置信区间（即2 倍标准差）。从图1 可见，在x∈[-2.5，2.5]区间内，灰色带宽较小，表明了在训练样本区间内，预测结果的预测方差较小，即不确定性较小；在x∈[-2.5，2.5]区间外，距离训练样本所在区间越远，灰色带宽越大，说明距离训练样本区间越远，预测结果的不确定性越大，进而导致出现较大误差的概率急剧增大（x=-3 或3时，曲线的偏差最大）。由此可见，GPR 模型的预测方差为预测结果的不确定性定理化评价提供了可能。

图1 GPR 回归预测示例Fig.1 Example for regression using GPR

3 高斯过程动态响应面法

3.1 基本思路

本文方法的基本思路是：首先，利用边坡分析程序生成少量学习样本，用以训练GPR 模型，利用训练后的GPR 模型重构功能函数，使隐式功能函数显式化；然后，将GPR 模型作为真实功能函数的替代工具，结合MCS 法计算失效概率，在MCS 大量抽样中选取失效域中的最接近于极限状态方程且不确定性较大的点作为最优样本点，利用边坡分析程序计算其真实功能函数值，由此获得1个新的学习样本，将该样本添入原学习样本集，GPR 模型重新学习，由此实现GPR 响应面在极限状态曲面附近拟合精度的自适应提高，进而再次结合MCS 法计算失效概率。不断重复上述的GPR 模型学习、应用MCS法计算失效概率以及搜索最优样本点等3个计算过程，直至收敛。值得指出的是，本文方法中，在MCS 随机抽样中，利用GPR 模型取代真实功能函数直接估计功能函数值，可以有效减小边坡重分析的次数，显著提高MCS 法的计算效率，从而实现边坡可靠性问题的快速求解。

3.2 关键技术

（1）构建基于小样本回归策略的GPR 响应面

在有限采样点条件下，建立高性能的响应面，实现真实隐式功能函数的高精度拟合与泛化，是降低可靠性分析方法对采样点规模依赖的关键所在。

GPR 具有坚实的统计学习理论基础，能很好地处理高维数、小样本和非线性的回归问题，具有实现容易、泛化能力强与参数自适应获取等优点，对高度非线性函数拟合具有良好的适用性。因此，仅以少量采样点为代价，采用模型最优超参数可自适应获取的GPR 模型重构功能函数，可以方便快捷地建立满足高效率精度要求的响应面代理模型。

为了展示GPR 的回归性能，下面以sinc 函数y=sin|x|/|x|（x=0时，y=1）为例，分别采用二次多项式、ANN 模型（BP 神经网络）和GPR 模型对加噪后生成的10个学习样本（x,y）分别进行回归分析。比较各回归模型在学习样本被噪音腐蚀的情况下拟合真实函数的效果。从图2 可看出，GPR 回归效果最好，它克服了二次多项式不适用于高度非线性函数拟合、ANN 在小样本问题中的过度拟合等明显问题，而且模型超参数可自适应获取。因此，与多项式和ANN 模型相比较，GPR 模型在小样本回归性能上具有一定的优越性。

（2）利用GPR 的动态学习更新响应面

响应面方法的计算精度主要取决于响应面对极限状态曲面的逼近程度。传统的ANN-MCS[3]、RBF-MCS[4]、SVM-MCS[8]等响应面法中，仅利用一次构建的预设学习样本来构造响应面。研究发现，当预设样本数过少或分布不合理时，对于高度非线性功能函数，高精度拟合是很难实现的。因此，为了提高计算效率，需要建立响应面拟合误差的高效修正机制。

图2 各种回归模型的拟合结果比较Fig.2 Regression result comparisons among different models

响应面法的关键是响应面对真实极限状态曲面（g(x)=0 对应的曲面）能很好地拟合。笔者构造一种迭代方式，以实现响应面的动态更新：将GPR 模型作为真实功能函数的替代工具，结合MCS 法进行大量随机抽样，然后从大量抽样中选取对真实极限状态曲面拟合效果影响最大点的作为最优样本点，计算该点的真实功能函数值，由此建立新的学习样本，添入到原学习样本集，应用GPR 模型重新进行学习，由此更新GPR 响应面。重复上述过程，不断利用上一迭代步的GPR 响应面，结合MCS 大量抽样，获得新的最优样本点，通过GPR 模型学习不断更新响应面。

通过响应面的动态更新，不仅能够极大地降低响应面对预设学习样本的依赖性，而且能够快速地改善响应面的拟合效果，加快迭代计算的收敛速度。值得指出的是，在上述迭代中，每一迭代步仅需进行1 次结构分析，确保了极低的计算代价。因此，这个迭代方式可以实现响应面对真实极限状态曲面的拟合误差的高效修正。

（3）利用GPR 不确定性评价功能获取最优样本点

本文方法中，实现响应面动态更新的关键在于对真实极限状态曲面拟合效果影响最大点——最优样本点的确定。对于最优样本点的评判标准，一种直观地想法是，鉴于极限状态曲面附近的样本点对响应面的拟合精度影响最大，可将失效域内最接近于真实极限状态曲面的样本点x*作为最优样本点，由此建立最优样本点的适应度函数：

对于真实极限状态函数，g(xi)=0，式（9）可改写为

研究发现，在学习样本空间之内GPR 模型的拟合精度相对较高，而在学习样本空间之外GPR 模型的拟合精度相对较低，根据式（10）估计的最优样本点往往落在学习样本空间内，GPR 重新学习后，学习样本空间内的GPR 响应面将更逼近于真实极限状态曲面，但在学习样本空间之外，GPR 响应面的拟合精度却难以保证。为了克服这一问题，需要在学习样本空间之外选取最优样本点。

学习样本空间之外的推断具有较大的不确定性。为了尽量减小结构重分析次数，本文采用小样本的回归策略，但是，以少量有限的信息去推断完整的信息必将承受一定的风险，了解并控制推断过程中的不确定性水平是保证所做推断有意义的前提。因此，在小样本推断的条件下，模型输出结果不确定性的合理描述是评价推断合理性的一个有效手段。在统计理论中，方差可以当作不确定性的一种度量。例如在经济学中，人们常依据方差进行投资项目的技术经济分析，在同等期望值条件下，方差值越小，则意味着投资项目的风险越小、回报较为稳定[15－16]。GRP 模型的最大特色在于能给出预测变量的均值和方差，方差可作为任意样本功能函数预测值的不确定性度量指标，即方差越大，该样本的功能函数预测值的不确定性越大。

为此，将预测方差 σ2引入式（10），可得到基于GPR 不确定性评价的最优样本点的适应度函数：

上式的物理意义是：失效域内，既接近于极限状态曲面且预测不确定性较大的点为最优样本点。

由GPR 的基本原理可知，GPR 预测方差较大的区域，一般出现在学习样本空间以外。根据式（11）进行样本点遴选，就能在学习样本空间之外选取接近于极限状态曲面且方差较大的最优样本点，由此有效地提升学习样本空间以外的GPR 响应面的拟合精度。从机器学习的角度来看，式（11）等式右边的分子部分控制了学习的精度，分母部分控制了学习的广度。

以图3为例，假设A 点与B 点的GPR 预测功能函数值几乎相等且接近于0，为最优样本点的候选对象。与A 点相比较，B 点位于学习样本空间之外，其预测方差较大，根据式（11），B 点的适应度较小，故B 点为最优样本点。利用B 点的坐标及其真实功能函数值，作为1个新的样本添入原训练样本集，重新训练GRP 模型，就可以实现学习样本空间之外的极限状态响应面的有效修正。

图3 最优样本点选取示意图Fig.3 Sketch of selecting the optimum sample points

3.3 实现步骤

假设结构的功能函数为Z=g(x)，基本随机变量x 的联合概率密度函数为f(x)，则结构失效概率为

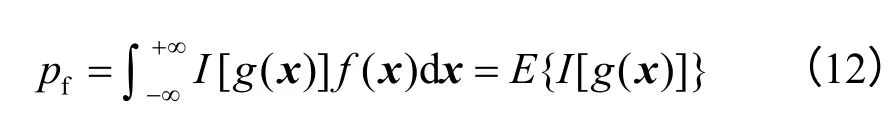
式中：I[g(x)]为g(x)的示性函数，当g(x)＜0时取1，否则取0。

采用MCS 法进行大量随机抽样，设样本容量为N，第k 次抽样的样本为xk，则pf的估计值为

根据式（7），利用GPR模型逼近真实功能函数：

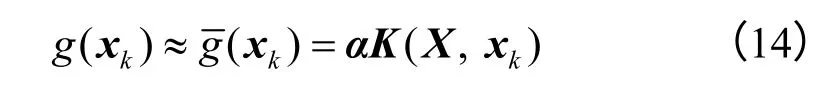
将式（14）代入式（13），可得到基于GPR响应面的失效概率估计式为

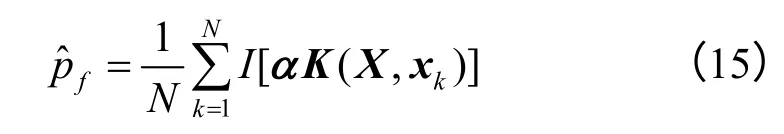
本文方法的实现步骤如下：

步骤1：通过边坡分析程序，计算功能函数值g(x1,x2,…,xn)与g(x1,x2,…,xi±fσi,…,xn)，从而构造2n+1个的学习样本，其中x 取均值点，f 取2[2,6]。

步骤2：采用GPR 模型对学习样本进行学习（自回归），建立真实功能函数的GPR 响应面，由此建立随机变量与功能函数值之间的非线性映射关系。

步骤3：根据各随机变量的统计特征，随机抽取N个（本文N=106）样本点，根据式（14），利用学习后的GPR 响应面推求相应地近似功能函数值。

步骤4：根据式（15）估计失效概率，若失效概率为0，返回步骤1，f 取上一次取值的1/2，增加2n个学习样本，重复步骤1～4，直至失效概率不为0。

步骤5：若前后迭代步之间的失效概率的相对差值小于1%，则停止迭代，否则，根据式（11），通过比对，从k个样本点中确定最优样本点。

步骤6：将最优样本点及其真实功能函数值作为新的最优样本，添入原学习样本集，返回步骤（2）。

根据上述步骤，编制了MATLAB 计算程序。

4 方法验证

下面给出了2个高度非线性功能函数的数值算例，采用本文方法计算时可假设其功能函数是隐式的，用来考查本文方法的可行性。

4.1 数值算例1

有一非线性功能函数为

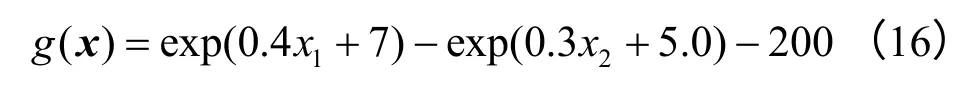
随机变量x1和x2均服从标准正态分布。

表1 列出了5个预设学习样本，采用GPR 模型进行学习，自适应获得的最优超参数对数值为lnθ=(1.50,2.91,7.86,-6.75)，预设学习样本的GPR 预测值可按下式计算：

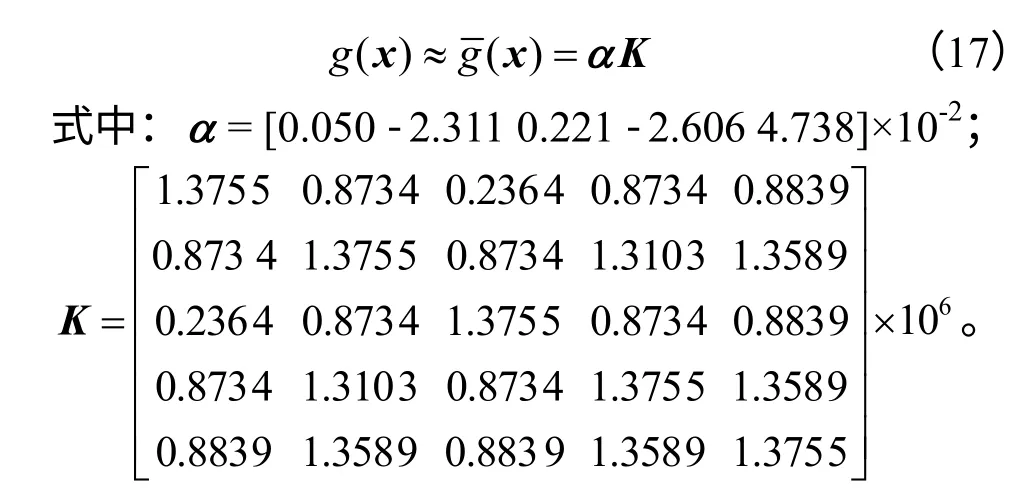
从表1 可看出，预设学习样本的GPR 预测值与真实功能函数值非常接近，说明学习后的GPR 模型可以在学习样本空间内很好地逼近真实功能函数，从而可以替代真实功能函数进行蒙特卡罗抽样。

表1 预设学习样本及其功能函数值Table 1 The learning samples and function values

计算迭代7 步后收敛，各迭代步的最优样本点及其失效概率计算值见表2。计算结果见表3，从中可见，以MCS 法模拟106次的结果为精确解时，与RSM、RBF-MCS、ANN-MCS 等响应面方法相比较，本文方法的求解精度最高，函数调用次数明显较少，其主要原因在于：①采用GPR 模型可以很好地拟合高度非线性的真实功能函数；②采用GPR 响应面动态更新技术，实现了极少数量采样点条件下GPR 响应面拟合精度的迅速提升（参见图4）。

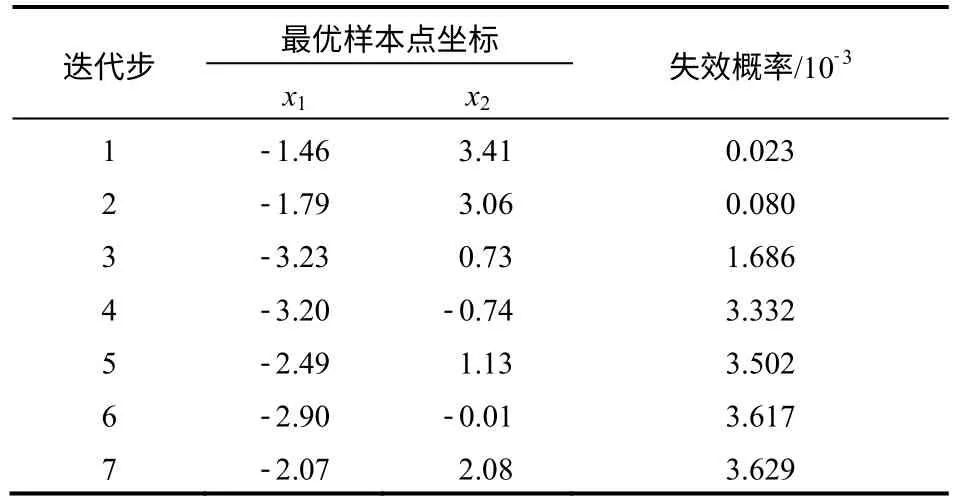
表2 各迭代步的计算结果Table 2 Results at different iterative steps

表3 数值算例1 的计算结果Table 3 Results of numerical example 1

图4 GPR 响应面的动态更新过程Fig.4 Dynamic updating process of GPR response surface

4.2 数值算例2

有一高次非线性功能函数为

随机变量x1、x2和x3均服从标准正态分布。

生成7个预设学习样本，计算迭代4 步后收敛，计算结果见表4。从中可见，以MCS 法模拟107次的结果为精确解时，FORM 法与RSM 法的相对误差均高达313%，本文方法的相对误差仅为4%，结果令人满意。该算例从数值试验的角度验证了本文方法适用于求解高度非线性隐式功能函数可靠性问题，能克服FORM 法、RSM 法等传统方法求解此类问题时计算误差偏大或计算不收敛的局限性。

表4 数值算例2 的计算结果Table 4 Results of numerical example 2

4.3 数值算例3

有一非线性功能函数为

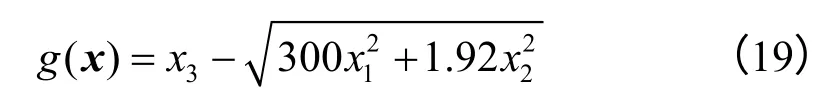
随机变量x1、x2和x3的统计特征见表5。

计算结果见表6。从中可见，以MCS 法模拟107次的结果为精确解时，与RSM 法相比较，本文方法计算精度较高，且函数调用次数明显较少。

表5 随机变量统计特征Table 5 Properties of stochastic variables

表6 数值算例3 的计算结果Table 6 Results of numerical example 3

5 边坡算例

下面给出边坡可靠性分析的3个算例，各算例均采用大型通用边坡分析商业软件SLIDE[16]提供的简化Bishop 法计算边坡安全系数K。

5.1 边坡算例1

有一均质边坡（见图5），设土的重度γ、黏聚力c 和内摩擦角φ 是相互独立的正态变量，统计特征如表7 所示。功能函数设为g=FS(c，φ，γ)-1，FS(·)为隐式函数，其函数值等于边坡安全系数K。构造的7个预设学习样本见表8，计算迭代4 步收敛，各迭代步所获得的最优样本见表9。

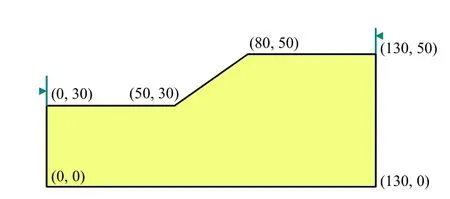
图5 单层边坡剖面图（单位：m）Fig.5 Geometry of one-layer slope(unit:m)

表7 单层边坡随机变量统计特征Table 7 Properties of stochastic variables of one-layer slope

表8 单层边坡预设学习样本Table 8 Initial learning samples of one-layer slope

表9 单层边坡各迭代步的最优样本Table 9 Optimum sample at different iterative steps of one-layer slope

计算结果见表10。从中可见，以MCS 法模拟106次的结果为相对精确解时，本文方法的相对误差为2.4%，边坡分析次数仅有11 次。若考虑随机变量服从相互独立的对数正态分布，对应的计算结果见表10，从中可见，本文方法的相对误差为1.1%，边坡分析次数仅有14 次。

表10 边坡算例1 的计算结果Table 10 Results of slope example 1 of one-layer slope

上述分析表明，本文方法计算精度令人满意，与MCS 法相比较，获取较高计算精度条件下所需要的边坡分析次数非常少。

5.2 二层边坡

有一非均质边坡（见图6），土坡包含二土层，土的重度γ=19 kN/m3，设黏聚力c，内摩擦角φ 是相互独立的正态分布变量，统计特征如表11 所示，功能函数设为g=FS(c,φ)-1。构造的7个预设学习样本见表12。程序迭代4 步收敛，各迭代步所获得的最优样本见表13。

图6 二层边坡剖面图（单位：m）Fig.6 Geometry of two-layer slope(unit:m)

表11 二层边坡随机变量统计特征Table 11 Properties of stochastic variables of two-layer slope

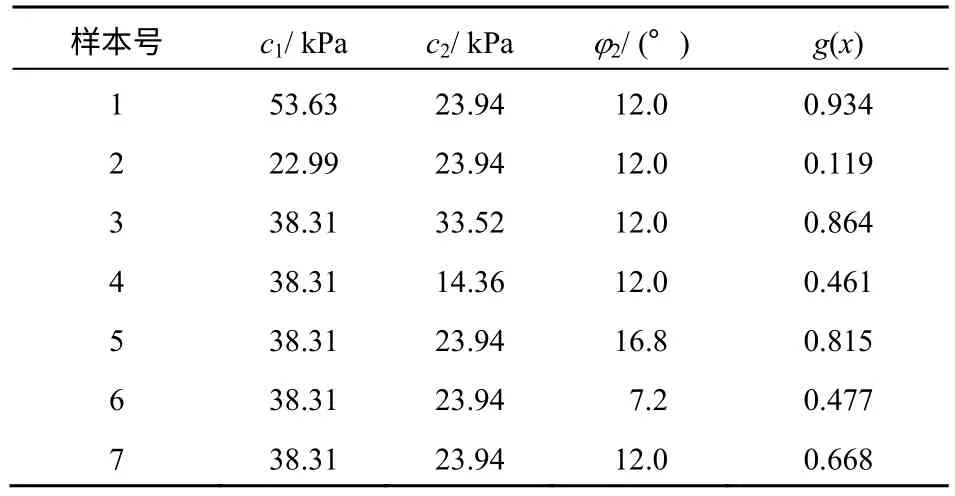
表12 二层边坡预设学习样本Table 12 Initial learning samples of two-layer slope

计算结果见表14，从中可知，以MCS 法模拟106次的结果为相对精确解时，本文方法的可靠指标相对误差为2.9%，边坡分析次数仅有12 次，在计算精度与计算效率上明显优于RSM、ANN-FORM与二阶 HDMR（high dimensional model representation）等不同响应面方法。若考虑随机变量服从相互独立的对数正态分布，对应的计算结果见表14，从中可见，与ANN-FORM 法[3]相比较，本文方法的计算精度较优，边坡分析次数明显较少。算例结果验证本文方法对于求解边坡可靠性问题的可行性与优越性。

表13 二层边坡各迭代步的最优样本Table 13 Optimum sample at different iterative steps of two layer slope

表14 边坡算例2 的计算结果Table 14 Results of slope example 2

5.3 多层边坡

Congress St.Cut model 是验证边坡可靠性分析方法的经典算例之一[18,20]，边坡剖面图及浸润线见图7。边坡各土层的力学参数见表15，其中黏土层1、黏土层2 与黏土层3 等土层的黏聚力c1、c2、c3为相互独立的正态随机变量。考虑的边坡失稳模式为边坡滑动面与第3 层（黏土层3）的下边界相切，对应的功能函数设为：g=FS(c1,c2,c3)-1。构造的7个预设样本见表16。计算迭代2 步收敛，各迭代步的最优样本见表17。

计算结果见表18。以MCS 法抽样106次[16]为相对精确解时，本文方法的计算精度明显优于二阶HDMR 响应面法[18]，边坡分析次数约为二阶HDMR响应面法[18]的1/7。若考虑随机变量服从相互独立的对数正态分布，对应的计算结果见表18，从中可见，本文方法边坡分析次数仅有10 次，但计算精度令人满意。

图7 多层边坡剖面图（单位：m）Fig.7 Geometry of multilayer slope(unit:m)

表15 多层边坡土体计算参数Table 15 Material properties of soil of multilayer slope

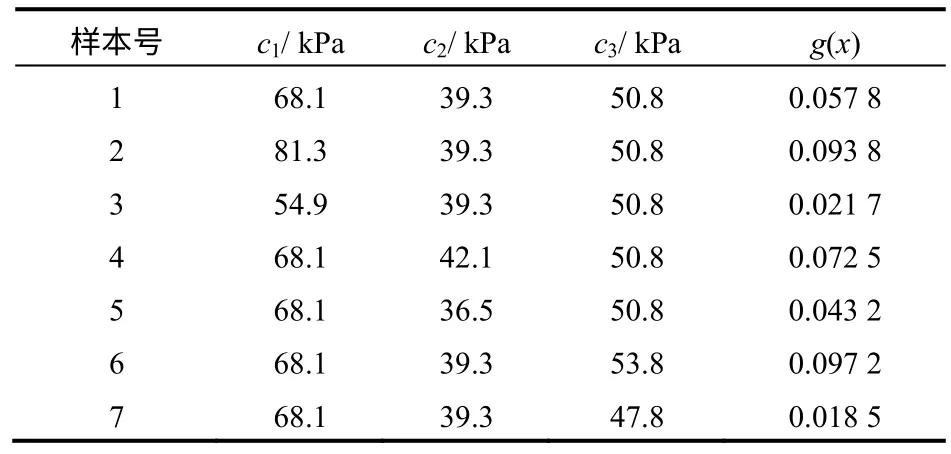
表16 多层边坡预设学习样本Table 16 The initial learning samples of multilayer slope

表17 多层边坡各迭代步的最优样本Table 17 The optimum sample at different iterative steps of multilayer slope

表18 边坡算例3 的计算结果Table 18 Results of slope example 3

6 结 论

（1）本文将GPR 响应面法与MCS 法相结合，提出了一种边坡失效概率估计的高斯过程动态响应面方法，该方法既利用了MCS 法对于功能函数的形式、维数及其分布形式均无特殊要求，计算精度高的优点，又充分利用了GPR 模型在处理小样本、非线性回归问题上的优势，此外，该方法还利用了GPR 模型提供的可对预测结果不确定度进行定量化评价的独特功能，在此基础上建立了响应面最优采样点的合理配置机制，并结合蒙特卡罗随机抽样，实现了响应面的高效率动态更新，进而有效地提升了响应面法的计算精度，加快了迭代计算的收敛速度。

（2）数值算例与边坡算例的研究结果表明，本文方法是可行的，它克服了经典响应面法求解高度非线性功能函数可靠性问题时计算误差大的不足，解决了MCS 法计算效率低、现有的“响应面+MCS”混合方法的计算精度过度依赖预设样本的规模与分布等瓶颈问题。

（3）与传统边坡可靠性分析方法相比较，本文方法具有计算精度高、估计速度快、易于与已有的边坡分析软件相结合的优点，计算过程中无需对功能函数求导数，故实现较为容易，便于工程应用，尤其适用于结构分析代价较高且具有高度非线性隐式功能函数的可靠性问题。

（4）受篇幅限制，本文算例仅考虑了随机变量相互独立、边坡滑面假设为圆弧的情况，对于随机变量相关性与非规则边坡滑面的情况，将另文阐述。

[1]刘晓,唐辉明,熊承仁.边坡动力可靠性分析方法的模式、问题与发展趋势[J].岩土力学,2013,34(5):1217－1234.LIU Xiao,TANG Hui-ming,XIONG Chen-ren.Patterns,problems,and development trends of analysis methods for slope dynamic reliability[J].Rock and Soil Mechanics,2013,34(5):1217－1234.

[2]KIM S H,NA S W.Response surface method using vector projected sampling points[J].Structural Safety,1997,19:3－19.

[3]CHO S E.Probabilistic stability analyses of slopes using the ANN-based response surface[J].Computers and Geotechnics,2009,36(5):787－797.

[4]DENG J.Structural reliability analysis for implicit performance function using radial basis function network[J].International Journal of Solids and Structures,2006,43(11－12):3255－3291.

[5]LUO X F,LI X,ZHOU J,et al.A Kriging-based hybrid optimization algorithm for slope reliability analysis[J].Structure Safety,2012,34(1):401－406.

[6]ZHAO H B.Slope reliability analysis using a support vector machine[J].Computers and Geotechnics,2008,35(3):459－467.

[7]GOMES H M,AWRUCH A M.Comparison of response surface and neural network with other methods for structural reliability analysis[J].Structure Safety,2004,26(1):49－67.

[8]LI D Q,CHEN Y F,LU W B,et al.Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables[J].Computers and Geotechnics,2011,38(1):58－68.

[9]蒋水华,李典庆,方国光.结构可靠度分析的响应面法和随机响应面法的比较[J].武汉大学学报(工学版),2012,45(1):46－53.JING Shui-hua,LI Dian-qing,PHOON Kokkwang.A comparative study of response surface method and stochastic response surface method for structure reliability analysis[J].Engineering Journal of Wuhan University,2012,45(1):46－53.

[10]HURTADO J E.An examination of methods for approximating implicit limit state functions from the viewpoint of statistical learning theory[J].Structural Safety,2004,26(3):271－293.

[11]RASMUSSEN C E，WILLIAMS C K I.GaussianProcesses for Machine Learning[M].Massachusetts:MIT Press,2006.

[12]SEEGER M.Gaussian processes for machine learning[J].International Journal of Neural System,2004,14(2):69－106.

[13]GIROLAMI M,ROGERS S.Variational Bayesian multinomial probit regression with Gaussian process priors[J].Neural Computation,2006,18(8):1790－1817.

[14]SU G S，YAN L B，SONG Y C.Gaussian process for non-linear displacement time series prediction of landslide[J].Journal of China University of Geosciences,2007,18：219－212.

[15]MARKOWITZ H.Portfolio selection[J].Journal of Finance,1952,7:77－91.

[16]朱奉云,邱菀华,刘善存.投资组合均值-方差模型和极小极大模型的实证比较[J].中国管理科学,2002,10(6):13－17.ZHU Feng-yun,QIU Wan-hua,LIU Shan-cun.An empirical comparison between mean-variance model and minimax model in Chinese stock market[J].Chinese Journal of Management Science,2002,10(6):13－17

[17]吕震宙,杨子政.基于神经网络的可靠性分析新方法[J].机械强度,2006,28(5):699－702.LU˙˙Zhen-zhou,YANG Zi-zheng.New reliability analysis method based on artificial neural network[J].Journal of Mechanical Strength,2006,28(5):699－702.

[18]ROCSCIENCE Inc.Slide 2D limit equilibrium slope stability for soil and rock slopes[R].[S.l.]:[s.n.],2006.

[19]XU B,LOW B K.Probabilistic stability analyses of embankments based on finite element method[J].Journal of Geotechnical and Geoenvironmental Engineering,2006,132(11):1444－1454.

[20]CHOWDHURY R N,RAO B N.Probabilistic stability assessment of slopes using high dimensional model representation[J].Computers and Geotechnics,2010,37(7－8):876－884.