考虑挤土效应的筒型基础沉放阻力数值分析及试验验证

杨 旭，陈 飞，练继建，王海军

（天津大学 水利工程仿真与安全国家重点试验室，天津 300072）

1 引 言

筒型基础是一种适合海上风机结构的基础，具有施工费用低、适用于不良地基、抗倾覆能力强、可重复利用等诸多优势，具有广阔的应用前景[1-4]。筒型基础的沉放安装是筒型基础能否实现工程应用的前提，因此，研究筒型基础沉放原理、计算沉放阻力是筒型基础研究的重要内容[3]。

筒型基础沉放过程一般分为两个阶段：在自重条件下的下沉；施加负压，进一步沉放。自重下沉阶段原理同静压沉放，在一些上部存在黏土或密砂夹层的土体中，由于黏土或密砂阻止了渗流的形成，其负压沉放阶段的阻力不受渗流减阻影响，可认为同静压沉放阻力一样[5]。此外，渗流减阻效应的研究也需对比负压沉放和静压沉放下沉过程中阻力变化情况，因此，研究筒型基础的静压沉放过程具有重要意义。目前传统筒型基础静压沉放阻力计算公式中筒壁内、外侧摩阻力计算方法相同[5]。随着一些窄深型或是带分舱板的宽浅型筒型基础的应用[6]，筒壁或分舱板的约束使得基础内侧挤土效应有时远大于外侧，应用传统公式不能反映真实挤土情况，计算沉放阻力可能存在较大误差。筒型基础沉放的数值分析多是在土体预留空隙，将筒壁预置，之后施加位移或力的边界条件分段贯入，或者采用单元生死法分批删除筒端下方土体单元[7]，这些方法只能实现筒型基础的分段沉放，同样难以反映基础下沉过程中筒壁对土体的真实挤压情况。

有鉴于此，为了更好地揭示筒壁内、外侧挤土效应的差异情况，需模拟筒壁从地表面到设计深度连续贯入土体的整个过程。沉放过程中土体扰动严重，筒壁、筒端附近土体单元严重扭曲，容易造成计算终止或是结果失真。一些学者使用任意拉格朗日-欧拉（Arbitrary Lagrangian Eulerian，ALE）技术模拟沉桩过程，取得较好结果[8]。本文将ALE 方法引入筒型基础沉放模拟中，模拟沉放过程中筒壁内、外侧挤土情况。为检验该数值方法的可靠性，开展了筒型基础静压沉放试验，并进行对比验证。

2 连续沉放数值模型

ALE 方法结合了纯 Lagrangian 分析和纯Eulerian 分析的优越性，它通过将材料运动和网格运动分别独立描述，从而有效地控制计算网格的扭曲、畸变，保证网格和计算质量。一个完整的ALE分析包括两个步骤：①建立一个新网格，②将旧网格的解答及状态变量传输到新网格上[9]。

图1为有限元计算简图，筒型基础沉放可以简化为一个轴对称问题，坐标采用柱坐标。由于其沉放过程中土体变形只在一定范围较大，为节约资源，仅对筒壁内、外侧一定范围的土体设置ALE 区域。由于采用了ALE 技术，物质点和网格节点在分析过程中不再保持耦合，节点处的位移和当前坐标不能代表物质点的移动，需定义追踪点来跟踪物质点的变化，这样可以得到追踪点变量随时间的变化过程，追踪点具体位置见图2。筒型基础采用刚体模拟，土体采用Mohr-Coulomb 模型。考虑筒壁内、外侧及筒端和相临土体的摩擦作用，其间设置面-面接触。紧靠筒壁和筒端的土体应力、应变变化剧烈，在这些地方单元网格加密处理，网格尺寸为筒壁厚度的1/4，以使其应力-应变达到满意的精度。

筒型基础沉放是筒壁缓慢贯入土体过程，选择准静态分析[10]，在一个足够大的时间内施加位移边界条件使筒壁缓慢贯入。分析初始，所有土体单元施加一个初始地应力，之后筒型基础施加位移边界条件至预定深度50 cm，位移线性增加。

图1 有限元计算简图Fig.1 Sketch of finite element calculation

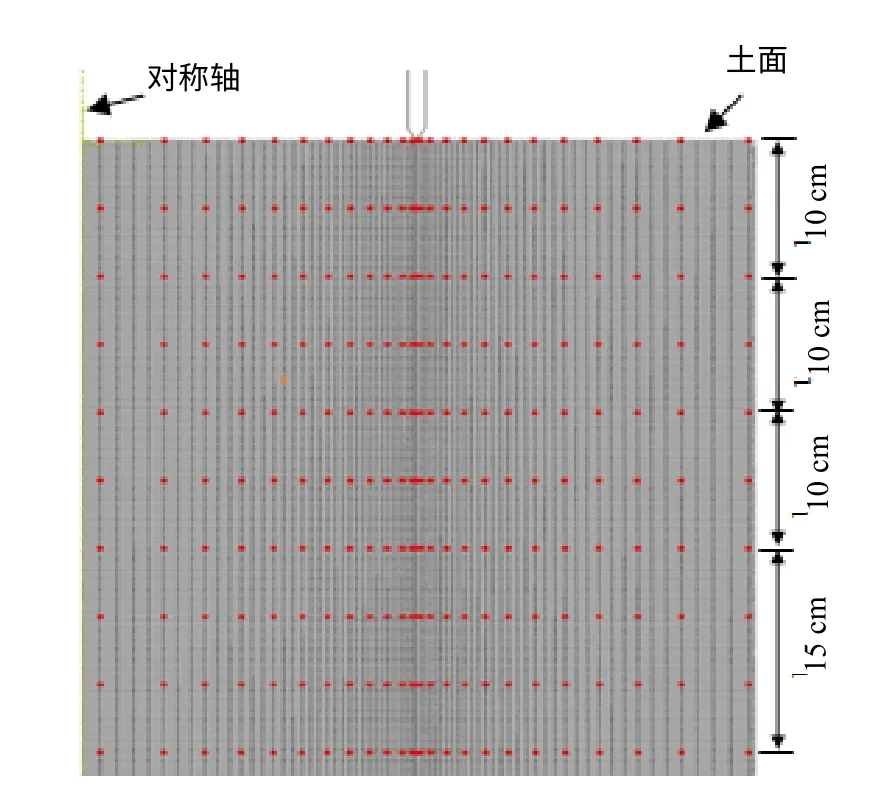
图2 追踪点位置示意图Fig.2 Locations of tracer points

3 数值模拟结果及试验验证

采用上述数值模型模拟了筒型基础静压沉放过程，并开展了模型试验对数值模拟结果进行验证，下面将模拟和试验结果进行详细介绍。

3.1 试验情况简介

模型试验采用砂土，砂土养护于4 m×4 m 的试验池中，土体厚度为1.5 m，土体处于饱和状态，水面高于土面0.15 m,如图3 所示。为保证土体均匀、密实，试验前采用振捣棒进行振捣养护。开展了直剪试验、固结试验、颗粒分析试验等土工试验来测量土质参数，由粒径分布曲线（见图4）结果对比港口工程地基规范[11]，土体中粒径大于0.25 mm 的颗粒超过总质量的50%，可知该试验砂土为中砂。土质参数如表1 所示。模型为钢质圆筒，直径为30.5 cm，壁厚为0.8 cm，筒壁高度为50 cm，传感器嵌入筒壁安装，具体布置位置如图4 所示。

图3 试验土体“粒径”分布曲线Fig.3 Particle size distribution curve of the soil in test

图4 模型试验Fig.4 Model test

静压沉放过程分为两个阶段：第1 阶段基础在自重作用下达到稳定；第2 阶段基础在液压系统的顶推下缓慢匀速下沉。

初始侧向土压力系数K0=1-sinφ（雅基公式），取为0.4，泊松比μ 取0.3[12]，土体-筒壁之间摩擦系数取0.5（tan0.7φ）[13]，其余参数取值同表1。

表1 试验测量土质参数Table 1 Soil parameters measured by test

3.2 筒壁内、外侧压力对比

筒体从土表面开始下沉，不同沉深下筒壁内侧所受土压力实测值与模拟值比较情况见图5。由图可见，模拟结果的整体变化趋势与试验结果一致，数值基本吻合。内侧土压力随着入土深度的增加其增长速度变快，这与Randolph 等[14]研究的管桩内侧土压力随深度指数增长的理论解是类似的。表2 列出了数值模拟和试验结果以及不同沉深下模拟值与初始状态下静止侧压力之比，由表可看出，内、侧筒壁挤压导致土压力大幅增长，可达初始压力的20倍以上。

表2 内侧土压力数值模拟与试验结果及初始压力对比Table 2 Computed and measured earth pressures of internal wall and the comparison with initial horizonal pressures

图5 筒壁内侧不同沉深数值模拟压力值同实测值对比Fig.5 Measured and computed earth pressures of the internal wall during penetration

图6为下沉至50 cm 的筒壁外侧压力模拟值与实测值的对比，由图可见筒壁外侧压力随沉深的增长趋势类似于筒壁内侧，但压力数值远小于筒壁内侧。筒壁内、外侧实测及模拟压力值见表3，由表可见，内侧压力为外侧压力的10 倍左右，表明下沉过程中筒内挤土效应远大于筒外。

表3 下沉至50 cm时的筒壁内外侧压力比较Table 3 Earth pressure comparison between the internal and external wall when sinking to 50 cm

图6 下沉至50 cm 的筒壁外侧数值模拟压力值与实测值对比Fig.6 Measured and computed earth pressures of the external wall when sinking to 50 cm

4 挤土效应机制分析

4.1 挤土位移

图7为筒内侧各追踪点在筒端贯入到该追踪点深度时的径向位移，挤土方向朝向中心对称轴。从图纵向比较可见，同一半径上追踪点位置越深，其径向挤土位移越大。从横向比较可以发现，除土表面曲线以外，其余曲线的径向挤土位移均是先增大后减小，直至接近对称轴时趋近于0。模型的轴对称性约束了对称轴处的径向挤土位移必须是0。挤土位移在靠近筒壁的一个小范围内（约1～3 cm）增大，分析有两个原因：由于是轴对称情况，筒内土体距筒壁越远，横向所占面积越小，在同样的挤土体积下，其径向挤土位移要大；筒壁下沉过程中对临近土体有剪切作用，造成土体剪胀，因而径向位移增大。而土表面上各点因可自由向上运动，且筒壁对该处土体剪切力很小，以上两个原因的影响消弱，因此，土面各点径向位移变化趋势一直是减小。

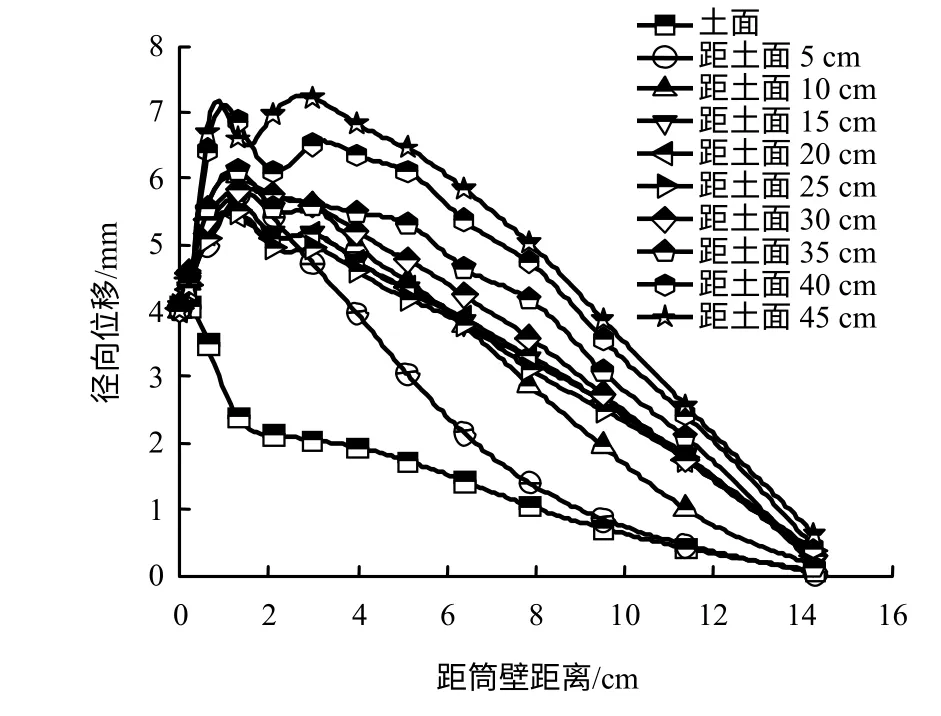
图7 筒内侧土体径向位移Fig.7 Radial displacements of soil inside the cylinder

图8为筒内侧各追踪点在基础下沉至50 cm时的竖向位移，正值表示位移向上。从图中纵向比较可见，同一半径上追踪点位置越深，其竖向挤土位移越小，即隆起越小，且表层土体因表面无约束，隆起明显比下层大。由横向比较可见，在筒壁的摩擦作用下，土体在靠近筒壁一定范围内（约2～3 cm）隆起高度小于其余点，在距土面20 cm 及更深处甚至出现负值，这与试验中观察到的筒壁附近土体出现下陷现象是一致的。

图8 筒内侧土体竖向位移Fig.8 Vertical displacements of soil inside the cylinder

图9为筒外侧各追踪点在筒端贯入到该追踪点深度时的径向位移，位移方向背离对称轴。曲线趋势与内侧大致相同，但挤土范围和挤土强度相比小很多。以距土表面5 cm 深处追踪点为例，如图10所示，筒壁外侧各点位移在距筒壁6 cm 及更远处基本为0，即该深度下筒壁对外侧土体径向挤土的影响仅到距筒壁6 cm 左右的位置；而筒壁对内侧土体挤压则影响到整个筒内土体，距筒壁距离15 cm。且距筒壁同等距离情况下内侧点比外侧点径向挤土位移大。

图9 筒外侧土体径向位移Fig.9 Radial displacements of soil outside the cylinder

图10 筒壁内外侧径向挤土位移对比Fig.10 Comparison of radial displacement between soil inside and outside the cylinder

图11为筒外侧各追踪点在基础下沉至50 cm时的竖向位移，正值表示土体向上隆起。曲线趋势与内侧基本相同，挤土范围与挤土强度相比小很多。以距土表面5 cm 深处为例，如图12 所示，外侧土体隆起较内侧小很多，且由于远处土体的约束，距筒壁越远，隆起越小，直至趋于0。

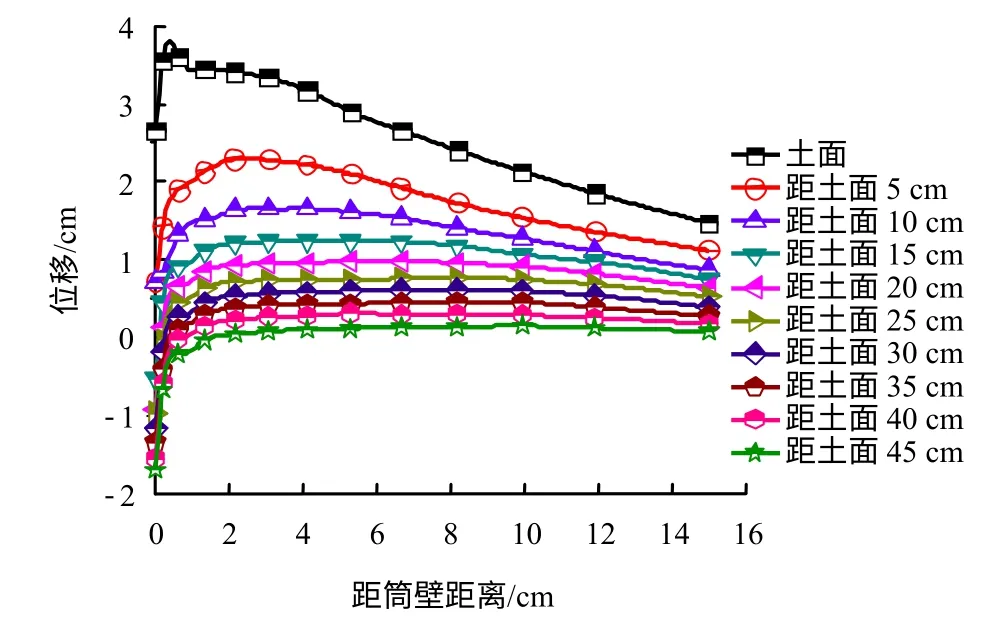
图11 筒外侧土体竖向位移Fig.11 Vertical displacements of soil outside the cylinder

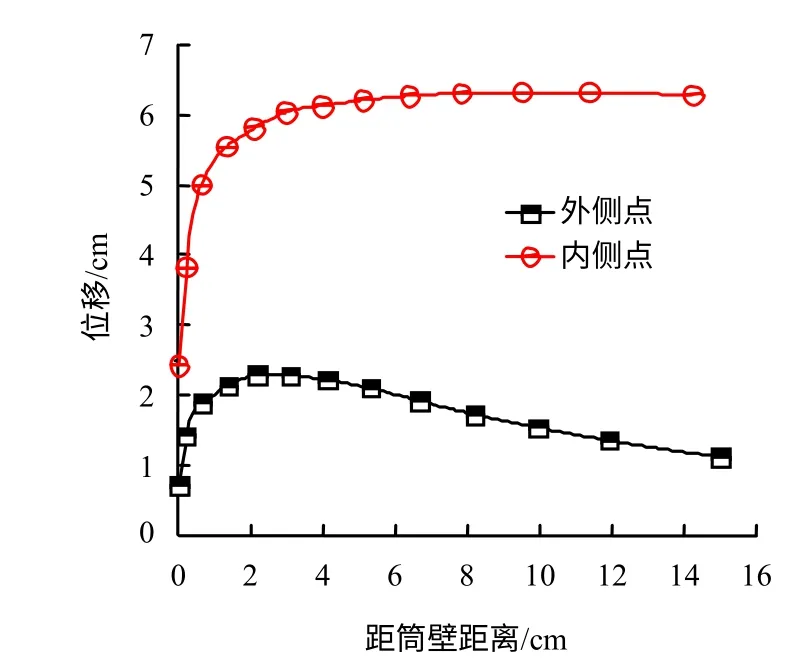
图12 筒壁内外侧竖向挤土位移对比Fig.12 Comparison of vertical displacements between soil inside and outside the cylinder

4.2 筒壁内、外侧土体应力

筒体下沉到50 cm时的应力云图如图13 所示。

图13 基础沉放至终点的应力云图（单位：kPa）Fig.13 Stress nephograms at the end of penetration(unit:kPa)

筒内土体径向应力在筒端附近达到最大值，之后沿筒壁向上应力迅速减小，云图成层状分布，由此可看出，筒壁的贯入对整个筒内土体的应力都有很大影响，与上文中筒壁内侧挤土位移影响范围一致。筒外土体的径向应力分布在筒端表现出明显的应力泡。竖向应力分布形式类似于径向应力，因筒壁摩擦作用，临近筒壁处的竖向应力较远离筒壁处大。筒外侧土体的竖向应力泡较径向应力泡长，成狭长状。切向应力是3个正应力中最小的，筒内侧土体在靠近对称轴处切向应力较大。筒外土体的切向应力应力泡形态介于竖向和径向应力之间。剪应力成常见的X 型分布，交叉点位于筒端处，筒内土体剪应力远大于筒外土体。

5 改进的阻力计算公式

筒型基础沉放总阻力Pf由侧壁阻力Qside和筒端阻力Qtip构成，侧壁阻力按照筒-土摩擦计算，筒端阻力目前主要基于地基极限承载力理论进行计算，传统阻力计算公式为

式中：qtip=0.5γ′tNγ+qNq；fs,av为沿筒壁高度方向摩阻力的平均值；为承载力系数；K为水平应力和初始竖向土应力的比值，API 规范中桩基承载力计算方法中，K 通常取为0.8；γ′为土体浮重度；φ为土体排水状态下的内摩擦角；δ为筒-土摩擦角，tanδ为摩擦系数，根据文献[13]建议取为0.5；t为筒壁厚度；D为筒体直径；z为下沉深度；Atip和Awall分别为筒端面积和筒壁内外侧面积。

一般情况下q=γz，因筒壁挤压和摩擦效果，竖向应力会大幅增大，并导致端阻力的增加，Clausen[15]提出用下式修正：

Andersen 等[5]将筒型基础沉放过程中的侧压力系数K 取为定值，即假设同一深度下筒壁内、外侧土压力大小相同，且土压力随深度线性增长。由前文分析可知，在沉深与筒径比大约为1.6时，筒壁内、外侧土压力相差很大，且均随深度非线性增长，传统K 值取法不适用。本文假设筒体下沉过程中土压力随深度呈二次曲线增长，即K 随深度呈线性增长，K=a(z/D)+b，假定土体表面(z=0)处K 取1，则b=1。图14 显示，用上述二次曲线形式计算出的筒壁内、外侧土压力同数值模拟结果吻合较好（此时内侧a=15，外侧a=0.8），带入式（1）、（2），αf取值为1，算得总阻力结果如图15 所示。

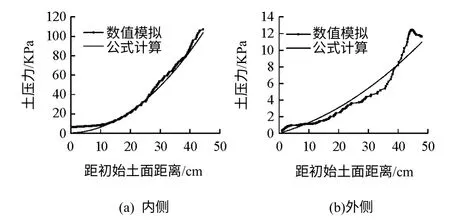
图14 筒壁内外侧土压力计算结果同数值模拟值对比Fig.14 Calculated and computed earth pressures of internal and external wall

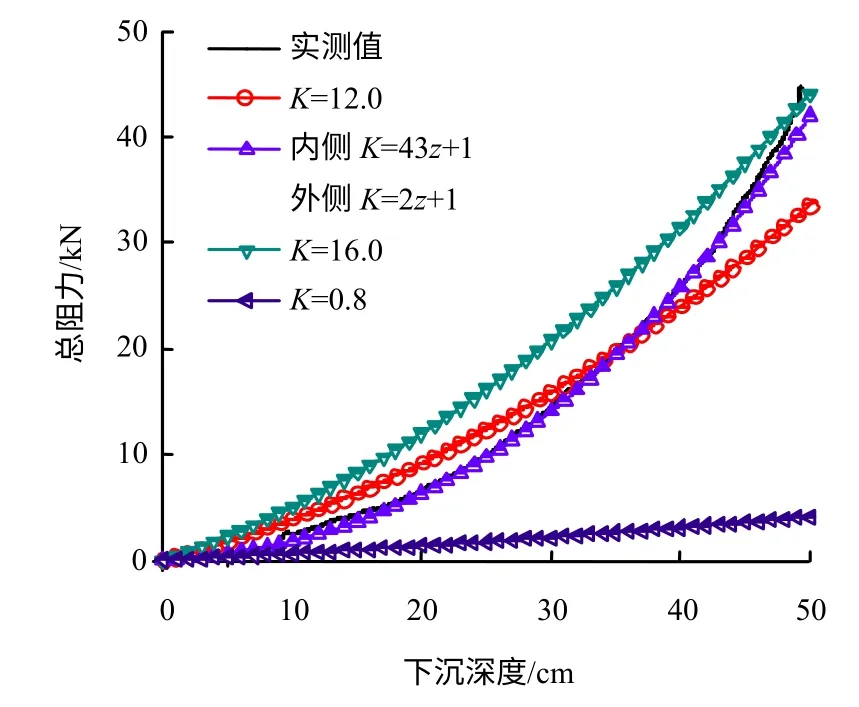
图15 不同K 值下沉放总阻力计算值同实测值对比Fig.15 Comparison of penetration resistance between measured and caculated results using different values of K

由图15 可见，改进后的公式计算的总阻力同试验结果拟合很好。为进一步研究筒型基础沉放过程中筒壁内、外侧的挤土效应，提取下沉到不同深度时筒壁内、外侧摩阻力值，内、外侧摩阻力比值随深度变化如图16 所示，由图可见，在相对沉深较小时，筒壁内、外侧摩阻力比值变化不大，约为2，之后比值逐渐变大，且增长速度很快，在大约1.6时达到10 倍以上。故筒型基础在相对下沉深度小于一定值（本例为0.3～0.4 之间），才可忽略筒壁内外侧挤土差异。

图16 筒内外壁侧摩阻力比值曲线Fig.16 Friction ratio of the internal wall to external wall

为验证上述方法，对文献[1]中提到的Europipe 16/11-E 导管架钻井平台现场试验进行数值模拟。表4为计算实测与结果的对比，可见沉深较小时由于总阻力数值较小，相对差值百分比较大，其余沉深的计算值与实测值吻合较好，初步验证了该方法的可靠性。

表4 16/11-E 总阻力计算值同实测值对比Table 4 Comparisons of measured and calculated penetrations resistance of 16/11-E

6 结 论

（1）本文采用ALE 方法，有效解决了筒型基础沉放模拟中土体网格扭曲过大问题，考虑基础和土体之间的摩擦作用，实现了筒型基础连续沉放的全过程数值模拟。通过与模型试验对比，证明了该种方法可较真实地模拟下沉过程中筒壁内、外侧挤土情况。数值模拟结果显示：在入土深度和筒径之比大约为1.6时，筒壁内侧土压力可达筒壁外侧压力的10 倍左右。数值模拟还可在某种程度上实现筒型基础沉放过程的动画仿真。

（2）由分析下沉过程中筒壁内、外侧土体的挤土位移以及应力分布可知，由于内、外侧土体约束条件和位移模式不同，内侧挤土范围及强度均大于外侧，导致内侧土体应力水平较外侧高，阐明了内、外侧挤土效应出现较大差异的机制。

（3）改进了传统不考虑内、外侧挤土差异的沉放阻力公式。本文结合数值分析及试验数据，考虑挤土效应，将筒壁内、外侧土压力系数分别取值，且将系数取为关于沉放深度z 的线性函数。与传统公式对比可见，改进后的公式总阻力计算结果与实测更为相符。数值模拟结果显示，只有在相对沉深（下沉深度/筒径）小于一定值（本例为0.3～0.4 之间）时，才可不考虑筒壁内外侧挤土差异。因此，对于一些窄深型或带分舱板的宽浅型筒型基础，其沉放阻力计算应考虑内、外侧挤土效应的差异。

本文仅研究了均质砂土中筒型基础的沉放过程，更复杂的土质条件下的沉放还需进一步的研究。

[1]LIAN Ji-jian,SUN Li-qiang,ZHANG Jin-feng,et al.Bearing capacity and technical advantages of composite bucket foundation of offshore wind turbines[J].Transactions of Tianjin University,2011,17(2):132－137.

[2]杨家岭,王书法,孔令伟,等.桶形基础采油平台三维有限元稳定性计算分析[J].岩土力学,2002,23(5):640－644.YANG Jia-ling,WANG Shu-fa,KONG Ling-wei,et al.The 3D finite element analysis of stability of platform with bucket foundation[J].Rock and Soil Mechanics,2002,23(5):640－644.

[3]袁中立,秦延龙,唐海燕.浅海桶形基础平台[M].北京:石油工业出版社,2010.

[4]于通顺,王海军.循环荷载下复合筒型基础地基孔隙水压力变化及液化分析[J].岩土力学,2014,35(3):820－826.YU Tong-shun,WANG Hai-jun.Pore water pressure fluctuation and liquefaction analysis of subgrade for composite bucket foundation under cyclic loading[J].Rock and Soil Mechanics,2014,35(3):820－826.

[5]ANDERSEN KNUT H,JOSTAD HANS PETTER,DYVIK RUNE.Penetration resistance of offshore skirted foundations and anchors in dense sand[J].Journal of Geotechnical and Geoenvironmental Engineering,2008,134(1):106－116.

[6]乐丛欢,丁红岩,张浦阳.分舱板对海上风机混凝土筒型基础承载模式的影响[J].工程力学,2013,30(4):429－434.LE Cong-huan,DING Hong-yan,ZHANG Pu-yang.Influences of bulkheads on the bearing mode of concrete bucket foundation for offshore wind turbine[J].Engineering Mechanics,2013,30(4):429－434.

[7]武科.滩海吸力式桶形基础承载力特性研究[D].大连:大连理工大学,2007.

[8]SHENG DAI-CHAO,NAZEM MAJIDREZA,CARTER JOHN P.Some computational aspects for solving deep penetration problems in geomechanics[J].Computational Mechanics,2009,44:549－561.

[9]NAZEM.Numerical algorithms for large deformation problems in geomechanics[D].Newcastle:The University of Newcastle,2006.

[10]BELYTSCHKO TED.连续体和结构的非线性有限元[M].庄茁,译.北京:清华大学出版社,2002.

[11]中华人民共和国交通部.JTJ 250-98 港口工程地基规范[S].北京:人民交通出版社,1998.

[12]中华人民共和国建设部.GB 50021-2001 岩土工程勘察规范[S].北京:中国建筑工业出版社,2001.

[13]American Petroleum Institute(API).Recommended practice for planning,designing and constructing fixed offshore platforms[R].Washington,D.C.:American Petroleum Institute,1993.

[14]RANDOLPH M F,LEONG E C,HOULSBY G T.One-dimensional analysis of soil plug in pipe piles[J].Geotechnique,1991,41(4):87－598.

[15]CLAUSEN C J F.Fundamentering av plattformer;Observasjoner og refleksjoner[C]//16th Laurits Bjerrum Memorial Lecture.Oslo:Norwegian Geotechnical Institute,1998.