三维层状饱和地基动力Green 函数的薄层法求解

王 鹏，史 吏，王 军，刘 凯

（1.温州大学 建筑与土木工程学院，浙江 温州 325035；2.浙江大学 软弱土与环境土工教育部重点实验室，杭州 310027；3.香港城市大学 科学与工程学院，香港）

1 引 言

Green 函数在土与结构动力相互作用分析中有重要应用，Wolf[1]解析推导了单相层状地基平面内、外运动的动力刚度矩阵，并运用到土-结构频域子结构法动力相互作用分析中。对于饱和地基，Halpern[2]采用柱坐标势函数分解和Hankel 积分变化求解了饱和半空间表面作用集中简谐荷载时，土骨架和孔隙水的竖向位移响应，并将此基本解运用于饱和半空间上覆刚性板动力阻抗函数的求解；Philippacopoulos[3]采用类似方法推导了饱和半空间表面施加竖向集中简谐荷载至土骨架时，土骨架的径向和竖向位移解，但仅给出了变换域中的位移谱图；陈胜立等[4]采用一组改进的饱和弹性土控制方程，通过Hankel 积分变换给出了饱和半空间埋置点荷载的轴对称Lamb 问题的积分解答，继而采用数值逆变换求解了地表竖向位移；王建华等[5]亦采用Hankel 积分变换方法求解了饱和半空间内部作用简谐竖向力时的Green 函数，饱和土体采用Biot 动力控制方程；王小岗[6]基于饱和土体Biot 动力控制方程，采用Fourier 级数展开和Hankel 变换给出了柱坐标下横观各向同性饱和半空间波动方程的非轴对称通解，在此基础上建立了饱和半空间的精确动力刚度矩阵，求解了柱面荷载作用下的层状横观各向同性饱和地基的动力Green 函数；丁伯阳等[7]采用饱和土体的Biot 波动方程，推导了固相和液相Green 函数频域解析解，并应用于饱和土中基桩动力特性分析中。

以上文献均采用积分变化法求解土体动力控制方程，最终所得空间-频域解答为含Hankel 函数的无穷积分。文献中多采用数值积分来完成上述无穷积分，从而不可避免地引入了截断误差，同时含Hankel 函数的被积函数在无穷积分区域上具有振荡特性[8]，数值积分方法的选择对积分结果稳定性和精确性的影响很大。时刚等[9]应用薄层法获得了层状饱和地基的Lamb 问题解答，并构造了适用于薄层法底层边界的通用旁轴近似解答。以上解答中，含Hankel 函数的逆变换是解析给出的，不再需要进行数值逆变换，从而简化了计算过程，提高了计算效率。

本文建立了三维层状饱和地基模型并在模型底边施加Degrande 等[10]提出的频域无反射边界条件，采用Fourier 变换和正交变换将饱和地基Biot 动力控制方程化为Love 和Rayleigh 模态方程，将地基沿深度方向划分为数个薄层单元并对单元位移场采用线性插值函数，从而将模态方程离散化，通过求解本征值问题，最终给出了三维层状饱和地基的频域动力Green 函数。在此基础上，分析了均质饱和地基的Love 和Rayleigh 模态的弥散特性，求解了均质和成层饱和半空间的 Lamb 问题，并与Philippacopoulos 的数值积分解对比，说明了所求Green 函数的正确性。文中所得Green 函数无需关于Hankel 函数进行数值逆变换且能直接计入地基的成层性，从而提高了计算效率。

2 层状饱和地基Green 函数

直角坐标系中，饱和土体Biot[11]动力控制方程为

本构方程为

式中：ui、wi(i=x,y,z)分别为土骨架和孔隙流体相对于土骨架的位移；λ、μ为土骨架Lame 常数；M、α为Biot 常数；ρ=nρf+(1-n)ρs，ρs、ρf分别为土骨架和孔隙流体的质量密度；m=a∞ρf/n，a∞为孔隙弯曲系数，n为孔隙度；b=ρfg/kD，kD为土体Darcy 渗透系数；θ=ui,i、ς=-wi,i分别为土骨架和孔隙流体的体积应变；σij为土体总应力；p为孔压。采用滞回阻尼表征土骨架的材料阻尼，即土骨架Lame 常数替换为λ*=λ(1+2iβ)及μ*=μ(1+2iβ)，其中i为单位虚数，β为滞回阻尼比。定义饱和土体特征频率为ωc=bρ/(mρ-ρf×ρf)[10]，对于不同的荷载激振频率ω，定义无量纲频率比为χ=ω/ωc。

定义Fourier 变换对和正交变换对分别为

式中：上标“^”表征波数-频率域变量；上标“-”表征正交变换域中的变量；kx和ky分别为与空间坐标x 和y 对应的波数，ω为圆频率；

利用Fourier 正变换将控制方程（1）～（4）变换到波数-频率域中，再针对位移和应力引入式（6）～（7）的正交变换，从而可将原本耦合的控制方程化为解耦的Love 和Rayleigh 模态控制方程，其对应的应力表达式亦为解耦的，见式（8）～（10）。

Love 模态：

Rayleigh 模态：

本构关系：

建立如图1 所示的层状饱和地基模型，在模型深度L 范围内（沿z 轴）划分为N个薄层，薄层厚度为hi（i=1～N）。各薄层土体材料性质相同，不同薄层之间的土体材料性质和厚度可以不同。模型底部施加Degrande 等[10]提出的无反射边界条件，从而模拟土体下卧半空间。

图1 三维层状饱和地基薄层法分析模型Fig.1 Thin layer element model of 3D layered saturated ground

由式（8）～（10）可知，控制方程均为关于坐标z 的常微分方程。对于特定薄层i，建立如图1右下角所示的局部坐标体系，并引入如下线性位移插值函数：

将式（8）～（9）代入式（11），运用Galerkin法，可得薄层i 的Love 和Rayleigh 模态积分弱形式控制方程如下所示。

薄层i 的Love 模态为

薄层i 的Rayleigh 模态为

对于由N个薄层组成的饱和地基模型，组装式（12）、（13）可得地表无应力时层状地基Love 模态和Rayleigh 模态的薄层法控制方程（由薄层i 的应力矢量表达式可知，层间应力在组装时会相互抵消）如下所示。

饱和层状地基Love 模态为

饱和层状地基Rayleigh 模态为

式中：

分别为模型的Rayleigh 和Love模态总体未知节点位移矢量；分别为模型Rayleigh 和Love 模态的总体节点应力矢量。

在地基模型底部施加Degrande 等[10]提出的无反射边界条件，从而模型底部的节点应力可表达为该节点未知节点位移的函数，如下式所示：

其中，矩阵元素bij(i,j=1,2,3)的表达式见文献[10]。若模型底边为固定边界，则有位移边界条件，此时与这些位移自由度相对应的应力将不出现在式（14）、（15）的右端项中。

将式（16）带入式（14）、（15）并移至方程左端，从而可得饱和层状地基Rayleigh 模态和Love模态的齐次控制方程，即形成了模型的本征值问题。求解Love 模态本征值问题可得2(N+1)个共轭特征值对kLm和对应的特征向量Φym(m=1～2(N+1))；求解Rayleigh 模态本征值问题可得4(N+1)个共轭特征值对kRm和对应的特征向量Φxm、Φzm(m=1,…,4(N+1))；但由于矩阵Gs和As中与节点自由度和对应的元素全部为0，从而使得Love 模态共有(N+1)个非零共轭特征值对，而Rayleigh 模态共有3(N+1)个非零共轭值对，且仅虚部为负的特征值方才满足无穷处的辐射条件。最终正交变换域中的位移可采用振型叠加法表达为

其中，

为第m 阶特征向量；qRm、qR′m和 qLm为对应的第m阶振型参与系数。

同理，作用

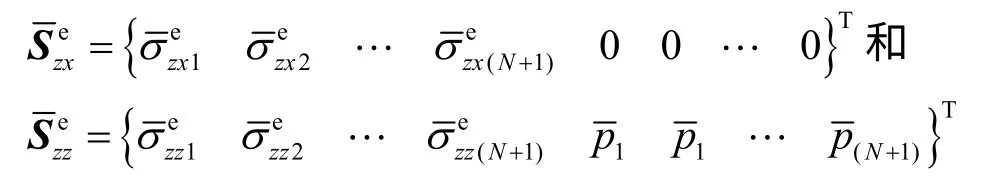
时，由式（15）和式（17）第1 式可求得以下两式：

将式（18）～（20）合写即可得正交变换域内的饱和层状地基Green 函数：

应用式（6）～（7）中的正交逆变换，将式（21）化为波数-频率域的Green 函数可有

式（22）中系数矩阵各元素表达式为

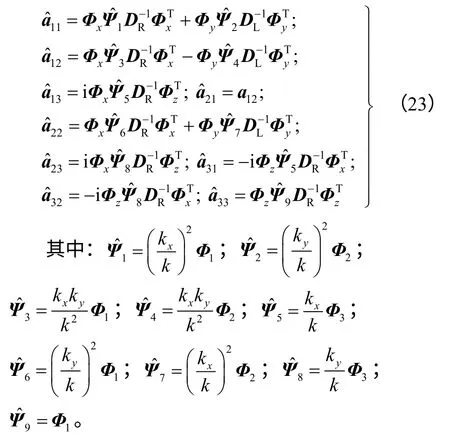
应用式（5）的Fourier 逆变换将式（22）变换至空间-频率域，注意到式（22）的系数矩阵中仅为波数kx和ky的函数，记其逆变换为(i=1～9)，可有

其中，函数F1(x)，F2(x)和F3(x)表达式为

薄层模型任意节点（激振点）施加集中点荷载至土骨架或孔隙流体时，各节点（观察点）的土骨架和孔隙流体位移响应可由式（25）算得。故式（25）为三维层状饱和地基空间-频率域的Green 函数。但由(i=1～9)的表达式可知，当激振点和观察点的平面距离r=0时会出现奇异性，此时可用等效均布圆环或圆盘荷载（分布半径为r0）代替点荷载来求解观察点位移响应。下文分析和结果呈现均在空间-频率域中进行，从而均省略变量上标“～”。

以上求解过程在Intel Visual Fortran®平台下采用Fortran 95 语言编写，本征值方程采用IMSL®数学包提供的子程序求解。

3 算例分析

3.1 均质饱和地基Love 及Rayleigh 模态

为研究不同渗透系数和激振频率（ω）下的饱和地基Love 及Rayleigh 模态的弥散特性，此处仅取均质单层饱和地基模型，模型底边固定。土体材料参数取文献[10]中的Molsand 参数，但渗透系数此处为可变值，模型参数如表1 所示。

表1 饱和土体材料及薄层参数Table1 Parameters of the saturated ground and the thin layer

图2 kD=1.0×10-4 m/s时Love 波数和Rayleigh 波数随激振频率的变化Fig.2 Variations of Love and Rayleigh wave numbers with respect to excitation frequency when kD=1.0×10-4 m/s

图3 kD=+∞(b=0)时Love 波数和Rayleigh 波数随激振频率的变化Fig.3 Variations of Love and Rayleigh wave numbers with respect to excitation frequency when kD=+∞(b=0)

由于模型底边固定，此时Love 模态只有1个非零特征值（波数）kL1，Rayleigh 模态则有3个非零特征值（波数）kR1、kR2和kR3。图2、3 分别呈现了渗透系数kD为1.0×10-4m/s 和+∞（b=0）时Love 波数及Rayleigh 波数随激振频率ω 的变化，波数实部（Re）代表了波的传播特性，虚部（Im）则代表了衰减特性。其中，横轴激振频率ω 无量纲化为ωL/cs0，，为饱和地基完全不透水时的剪切波速；纵轴波数k(k=kL1,kR1,kR2,kR3)无量纲化为kL。

由图2(a)可知，Love 波在激振频率低于S 波的截止频率时，kL1实部为0，即此时Love 波并不传播。而当激振频率高于截止频率时，其实部随ω 线性增加，但虚部接近于0，即此时Love 波是传播的；由图2(b)可知，kR1的实部和虚部均随激振频率明显增大，即该Rayleigh 波是传播的，但很快衰减。且该波在激振频率很小时就已传播，无截止频率；由图2(c)可知，此Rayleigh 波仅在ω 高于P1 波的截止频率时方才传播，且衰减很小；由图2(d)可知，该Rayleigh 波存在两个截止频率，分别对应S 和P1的截止频率。当ω 介于二者之间或大于P1 截止频率时，该波是传播的，且衰减很小。当前渗透系数下，对于表1 中的激振频率变化范围，无量纲频率比χ ＜ 0.01，此时P2 波传播速度很小可忽略不计，且其衰减系数远较P1 波和S 波为大，故而图2 Rayleigh 波传播特性中并未体现P2 波截止频率的影响。

对比图2、3 可知，渗透系数变化对kL1和kR3影响很小，但对kR1和kR2影响很大。当前渗透系数下，使得饱和地基的特征频率ωc为0，即χ为无穷大，此时P2 波速大于S 波速，故而kR2中体现了P2 波截止频率的影响。

3.2 均质饱和半空间Lamb 问题

为验证所得Green 函数的正确性，运用式（24）求解了均质饱和半空间的Lamb 问题并与Philippacopoulos[3]的数值积分解进行对比。被积函数包括了Hankel 函数，为振荡积分，此处采用Hidenori[8]提供的方法完成数值积分。饱和土体材料参数同表1，渗透系数kD=1.0×10-4m/s。

图4为无量纲频率比χ=0.01 和0.10时，薄层法和数值积分法所得半空间表面土骨架竖向位移（uz）的对比图。图中横坐标r为激振点与观察点之间的平面距离，无量纲化为r/λs0，其中λs0=2π cs0/ω；纵坐标uz无量纲化为uz/uz0，其中uz0为均质单相弹性半空间的Boussinesq 解。单相弹性半空间的材料参数μ 和ν 同表1。薄层法求解时，模型深度L=10 λs0，各薄层厚度h=λs0/6，薄层总数N=60，。经试算，数值积分法在包括Bessel 函数前2 000个0 点时，数值积分结果趋于稳定，此处取前3000个0 点。

图4 均质饱和半空间Lamb 问题薄层法求解与数值积分法求解对比Fig.4 Comparison between the thin layer element method and numerical integration solutions of Lamb problem of saturated homogeneous ground

由图4 可知，薄层法与数值积分法的结果变化趋势完全相同，且两种方法给出的竖向位移值十分接近，由此说明了所得Green 函数的正确性。注意r/λs0＜0.5时，Hidenori 方法引入的截断误差导致了数值积分解的波动。

3.3 成层饱和半空间Lamb 问题

为研究地基成层性的影响，此处考虑上软、下硬双层饱和半空间的Lamb 问题。第1 层饱和土体参数同表1、层厚记为L1、最短波长记为λs1=2π cs1/ω，其中，μ1为土层1 的剪切模量,各薄层厚度h1=λs1/10；第2 层饱和地基土体参数除剪切模量μ2=2μ1外，其余参数同表1，厚度为L2、最短波长记为λs2=2π cs2/ω，其中，各薄层厚度h2=λs2/10。两层地基的渗透系数kD均为1.0×10-4m/s。计算时，L2=4λs2，L1则分别取为0.2λs1、0.5λs1、λs1和4λs1，无量纲频率比χ=0.01。半空间表面土骨架竖向位移（uz）计算结果如图5所示，其中横坐标为无量纲激振频率ωr/cs1，纵坐标无量纲化为uz/uz0，uz0为均质单相弹性半空间的Boussinesq 解，弹性半空间的材料参数μ 和ν 同土层1。

图5 上软下硬双层饱和地基Lamb 问题Fig.5 Lamb problem of two-layer saturated ground(soft up layer and stiff second layer)

由图5 可知，土体分层对土骨架竖向位移的影响十分明显：L1/λs1=0.2时位移幅值较低；L1/λs1=0.5时位移幅值增大；L1/λs1增大至1 和4时则位移幅值减小，但位移变化趋势趋于一致。

4 结 论

（1）渗透系数变化对Love 模态影响很小，对Rayleigh 模态有明显影响。

（2）Love 波和Rayleigh 波在饱和地基中传播时存在截止频率。

（3）本文所得Green 函数是正确的，且无需关于Hankel 函数进行数值逆变换，提高了计算效率。

（4）土体分层对地表位移响应有明显影响，本文所得Green 函数能直接考虑地基土体的成层性。

[1]WOLF J P.Soil-structure-interaction analysis in time domain[M].[S.l.]:Prentice Hall,1988.

[2]HALPERN M R.Response of poroelastic halfspace to steady-state harmonic surface traction[J].International Journal for Numerical and Analytical Methods in Geomechanics,1986,10:609－632.

[3]PHILIPPACOPOULOS A J.Lamb’s problem for fluid-saturated,porous media[J].Bulletin of the Seismological Society of America,1988,78(2):908－923.

[4]陈胜立,张建民,陈龙珠.饱和地基中埋置点源荷载的动力Green 函数[J].岩土工程学报,2001,23(4):423－426.CHEN Sheng-li,ZHANG Jian-min,CHEN Long-zhu.Dynamic Green’s functions of saturated soils subjected to the internal excitation[J].Chinese Journal of Geotechnical Engineering,2001,23(4):423－426.

[5]王建华,陆建飞,沈为平.半空间饱和土在内部简谐垂直力作用下的Green 函数[J].水利学报,2001,3:54－57.WANG Jian-hua,LU Jian-fei,SHEN Wei-ping.The Green function of harmonic vertical load applied on the interior of the half space saturated soil[J].Journal of Hydraulic Engineering,2001,3:54－57.

[6]王小岗.横观各向同性饱和土中柱面荷载的动力Green 函数[J].力学学报,2010,42(5):909－918.WANG Xiao-gang.Dynamic Green’s function for internal barrel loads in transversely isotropic saturated soils[J].Chinese Journal of Theoretical and Applied Mechanics,2010,42(5):909－918.

[7]丁伯阳,童晓刚,陈军,等.排水状态下饱和土中基桩动力特性分析[J].岩土工程学报,2013,35(1):85－95.DING Bo-yang,TONG Xiao-gang,CHEN Jun,et al.Dynamic properties of a single pile in saturated soil under drainage[J].Chinese Journal of Geotechnical Engineering,2013,35(1):85－95.

[8]HIDENORI OGATA.A numerical integration formula based on the Bessel functions[J].Research Institure for Mathematical Sciences, 2005,41:949－970.

[9]时刚,高广运,冯世进.饱和层状地基的薄层发基本解及其旁轴边界[J].岩土工程学报,2010,32(5):664－671.SHI Gang,GAO Guang-yun,FENG Shi-jin.Basic solution of saturated layered ground by thin layered method and its paraaxial boundary[J].Chinese Journal of Geotechnical Engineering,2010,32(5):664－671.

[10]DEGRANDE G,ROECK G D.An absorbing boundary condition for wave propagation in saturated poroelastic media——Part I:Formulation and efficiency evaluation[J].Soil Dynamics and Earthquake Engineering,1993,12(7):411－421.

[11]BIOT M A.Theory of propagation of elastic waves in afluid saturated porous solid.I:Low frequency range[J].Journal of Acoustic Society of American,1956,28(2):168－178.

[12]蒋通.地基-结构动力相互作用分析方法——薄层法原理及应用[M].上海:同济大学出版社,2009.