在几何教学中培养学生的逻辑思维与推理能力

富锦市宏胜中学

在几何教学中培养学生的逻辑思维与推理能力

富锦市宏胜中学崔宏云

证明题的教学对培养学生的逻辑思维和逻辑推理能力，有着重要的作用.而这种能力的培养和提高是通过教师的指导，通过教学过程乃至每个细小的教学环节来实现的.大多数学生面对证明题感觉无从下手，说理过程条理不清，东一句西一句.为了使学生掌握证明题的解题技巧，提高解题能力，现把自己在工作中的心得和同行交流一下.

一、学生必须深刻理解掌握几何中的定义、公理、定理、推论等证明题的根据

在教学中结合实际生活经验，讲清概念的由来、意义、性质.它与相关的概念有什么联系与区别.为了加强学生的记忆，将相关的知识进行综合，利用图表法、归纳法进行教学，从而使学生对所学知识能够全面系统地掌握.

如平行四边形的性质和判定可归纳为：从边、角、对角线三方面来记忆：

具备其中任意一条的四边形，就可以得到它是平行四边形，则其他几条都成立.

二、帮助学生弄清命题的条件和结论

在讲解例题时指导学生了解命题的结构，理解一些关联词.例如“如果……，那么…….”或“若……，则…….”等形式.“如果”开始的部分是题设，“那么”的部分是结论，对于省略关联词的命题，如“等腰三角形两底角相等”.要引导学生如何寻找条件和结论，并举出各式各样的命题类型，让学生反复训练，加深理解.

三、拓宽学生思路，掌握多种证明方法

在教学过程中要拓宽学生的解题思路，掌握多种论证方法和技巧，因为几何证明题往往都是独具匠心，命题复杂，所以应培养学生多方位多角度去思考、论证.使学生在解题过程中常有“山重水复疑无路，柳暗花明又一村”的感觉.

（一）由果导因.有些证明题从条件入手有难度，可以从命题的结论开始，由果导因追溯到已知条件，这样问题就可以迎刃而解.“要证伊伊只要证伊伊要证伊伊只要证伊伊；……”然后把分析过程颠倒过来，就能够轻松地写出解题过程.

（二）架桥铺路.从要证明的等式两端出发，使他们都等于第三者，架设一个桥梁把等式两端联系起来.例如：如下图，在荀ABCD中，E是CD的中点，△ABE是等边三角形，求证：四边形ABCD是矩形.

欲证荀ABCD是矩形，需证∠C=90°或∠D=90°.

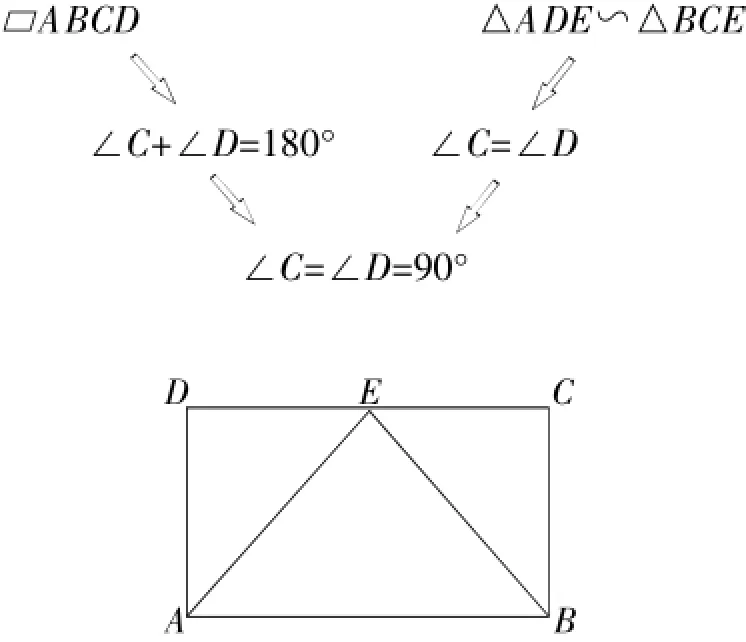
分析：要证蚁C=90毅或蚁D=90毅，因为已知条件中没有90毅的角，只知道蚁C+蚁D=180毅.这时要能再使蚁C=蚁D即可，而这两个角又分别位于两个三角形中.所以找到满足这两个三角形全等的条件为突破口，给欲证架设桥梁.通过分析可利用AD=BC、DE=CE、AE=BE来证△ADE易吟BCE.

（三）一题多解，对于一道命题的证明，不能让学生生搬硬套，要培养他们拓宽思路，寻找不同的解题方法.

例如：如图，荀ABCD中，AE平分蚁BAD交BC于点E，CF平分蚁BCD交AD于点F，求证：四边形AECF是平行四边形.

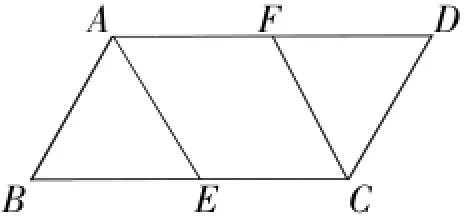
还可以用其他方法来进行证明.只要能达到解决问题的目的，若能一题多证，则妙趣横生，就会获得较好的教学效果.

四、培养学生能够准确地画出图形

在证明时如果题中没有给出图形的，要让学生正确地画出图形.这样可帮助学生观察和分析问题，不容易出错.还有的题目须要画出辅助线的才能证明出结论，这样就须要教师教给学生如何填辅助线.对于文字题要根据命题的内容，画出相应的几何图形，标上字母，然后用数学语言写出已知与求证。画图时注意不要画特殊的图形.

培养学生正确地运用几何语言及符号，养成规范的书写格式.要让学生掌握正确的书写格式和推理过程，发现不规范的药及时纠正，让学生多阅读课本上的例题，提高他们的推理过程.

适当地做一些典型的练习题，使学生在做题中总结经验，吸取教训.也能使学生在多做题过程中熟能生巧，不断提高他们证明题的能力，从而培养了他们的逻辑思维与逻辑推理能力.

E-mail:88686329@qq.com

❖编辑/张烨